力傳感器模型辨識及動態補償器設計*

王鏡森 曹家勇 姚淳哲 吳玉春

(上海應用技術大學機械工程學院，上海 201418)

近年來，隨著我國制造業的飛快發展，自動化生產線與智能制造技術不斷完善，對力檢測系統的動態特性的要求也隨之不斷提高。力傳感器作為力檢測系統的最前端，如果動態性能不能達到使用要求，也就不能快速、無失真地反應隨時間變化的動態力信號，使力檢測系統擁有較大的動態誤差。例如在機床檢測與故障診斷過程切削檢測的應用場合，切削力變化頻率快、成分復雜，檢測精度要求高。需要在現有傳感器基礎上，利用數字化動態補償技術，有效改善檢測系統的頻響特性。在這種背景下，對力傳感器進行動態補償是改善力傳感器動態特性的一條有效途徑。動態補償常用的方法包括零極點配置法、系統辨識法、神經網絡算法等[1-8]。其中零極點配置法原理簡單，較易實現。

建立準確可靠的傳感器模型對研究傳感器動態特性至關重要。目前國內外對建立傳感器數學模型的研究已經比較成熟，常用的模型辨識方法主要有兩種[9]：一種是根據傳感器的結構特性與工作原理推導出傳感器系統的數學模型；另一種方法是通過實驗采集傳感器輸入輸出的數據并進行系統辨識建模。文獻[10]介紹了一種傳統的即通過手工描點法繪圖，然后手工量取相關量進行計算的方法。這種分析方法顯然工作量巨大，而且計算精度差，所得模型誤差較大。文獻[11]提出一種最優化建模方法，使傳感器系統在誤差允許的范圍內簡化為較簡單的模型，這種方法計算量較小，且所求得的模型更簡單。文獻[12]研究了最小二乘法在系統辨識中的應用，將沃爾什函數應用于最小二乘法參數辨識中。文獻[13]提出了一種改進的具有更快收斂速度和和更強魯棒性的FLANN，該網絡成功用于壓力傳感器動態建模。文獻[14-15]使用神經網絡辨識的方法，建立了傳感器的辨識模型，通過跟蹤補償環節的變化可以獲得傳感器特性的各種變化。

1 力傳感器模型辨識

為了獲取力傳感器的動態性能指標(阻尼比，固有頻率)，需要對其進行動態建模。建立傳感器數學模型有兩種方法：一種解析法，是使用各種物理定律以及系統的結構數據推導出模型；另一種方法是利用實驗數據辨識出系統模型，稱為系統辨識法。

1.1 系統辨識法

系統辨識的具體過程是指通過對傳感器采集其輸入和輸出數據并進行動態標定，使用系統辨識的方法獲取傳感器一定形式的數學模型。系統辨識的特點是把傳感器系統看成一個黑箱，僅僅依據實驗數據建模。這種方法能夠充分獲取傳感器的動態特性并且簡單易行。通過系統辨識獲得的模型并不直接反映出傳感器的結構特性和工作原理。由于這種方法無須深入了解傳感器的結構特性與工作機理，因此系統辨識方法非常具有實用性。系統辨識法中應用最小二乘法辨識模型參數的研究已經相當完善，被廣泛應用。

1.2 非線性最小二乘法估計參數

設使用一非線性函數f(c,x)對已知一組實驗數據(xi,yi)(i=1,2,…,m)進行擬合，其中c=(c0,c1,…,cn)為待擬合系數。首先給擬合系數一個初始值，并記為cj(0)(j=1,2,…,m),且使

cj=cj(0)+δcj

(1)

如果能夠確定δcj，則可確定cj的值。為求出δcj，將擬合函數f(c,x)在cj(0)附近作泰勒級數展開，并略去δcj的高次項，當x=xi時有

(2)

式(2)中，

f0(c,xi)=f(c0(0),c1(0),…,cn(0),xi)

(3)

(4)

如果可以確定待擬合函數的函數形式，并已知實驗數據xi時，選定合適的cj(0)，可求出式(3)及式(4)，這樣函數f(c,x)就可以簡化看作一個關于變量δcj的線性函數。

可根據最小二乘法定義函數f(c,x)擬合殘差的平方和為：

I=∑[f(c,xi)-yi]2

(5)

將(2)代入式(5)得：

(6)

由式(6)可知，I是關于δcj的函數。當?I/?δcj=0時，可以確定δcj的值，即

(7)

整理式(7)得法方程：

A×C=B

(8)

在式(8)中：

(9)

B=(b0,b1,b2,L,bn)T

(10)

C=(δc0,δc1,δc2,L,δcn)

(11)

在矩陣A中，

在列向量B中，

在已知數據(xi,yi)和cj(0)后，就能夠通過解法方程求出δcj的值。

當求得的|δcj|比較大時，可以通過式(1)進行迭代計算，直到|δcj|可以忽略為止，從而得到最終的cj值,得到辨識模型。

2 動態補償環節設計

2.1 動態補償原理

動態補償的實質就是在傳感器原有的系統特性下串聯一個動態補償濾波器，拓寬原傳感器系統通頻帶，使瞬態信號的全部或主要頻率分量不被改變。在補償設計時，由于存在測量噪聲，這就導致補償后高頻信號的放大引起噪聲的放大，噪聲會嚴重污染測量信號，甚至使得補償失去意義。對此，可以在滿足測量要求的前提下考慮添加非理想補償環節。動態特性補償原理如圖1所示。

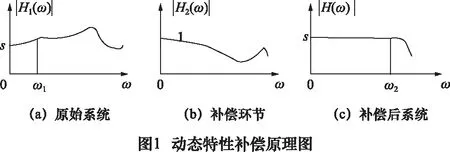
圖1a中的截止頻率ω1通過添加圖1b補償環節將其截止頻率拓寬到圖1c中的ω2，傳感器系統的工作頻帶變寬，能夠通過系統的頻率分量變多，可以更好復現原輸入信號的動態特性。

2.2 零極點配置法設計補償環節

傳感器系統的動態性能指標與傳感器系統的傳遞函數零極點位置有密切聯系。通過在傳感器后串接一個補償環節，可以將原傳遞函數不符合要求的極點相消除，重新調整新加入的極點位置，使傳感器的動態特性滿足實際使用要求。零極點配置法設計動態補償環節簡單易行，且補償效果好。零極點配置法設計動態補償環節的實現可以是各種各樣的。

假設傳感器為二階系統時，其離散傳遞函數為

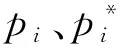
響應的動態補償器為

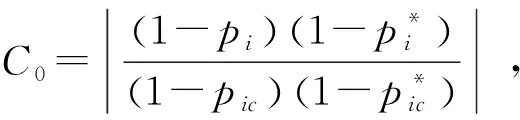
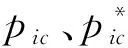
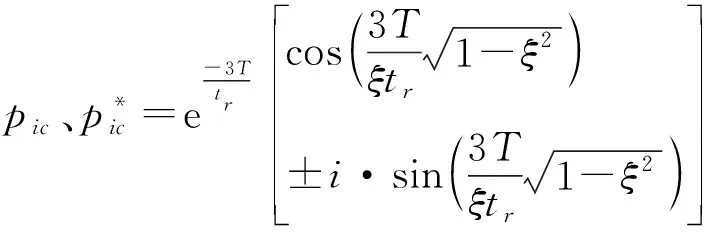
由于在零極點配置法設計動態補償環節過程中，需要依據傳感器的傳遞函數對零極點進行分析。因此，要求傳感器模型精度較高，但并不嚴格。零極點配置法適用于響應曲線上升時間長、調節時間長且超調量大等動態特性較差的傳感器系統。

3 實驗驗證與系統實現

現選擇如圖2所示一雙彎曲梁力傳感器進行實驗,采集數據。具體實驗裝置組成包括力傳感器、信號放大器、數據采集卡和數據處理軟件。其中力傳感器選擇常用的雙彎曲梁力傳感器，信號放大器放大倍數為1 000倍，數據采集卡選擇同步高速數據采集卡(USB_ HRF4626)，數據采集軟件界面如圖3所示，數據處理軟件選擇Matlab實現。

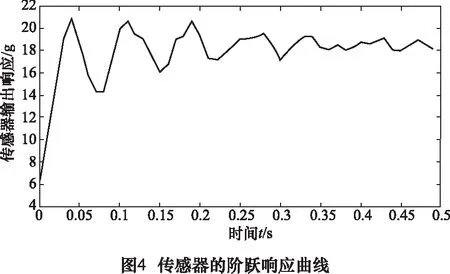
使用該實驗裝置進行傳感器的階躍響應實驗數據采集，采集頻率為1 000 Hz。并對該傳感器進行靜態標定，得到該力傳感器的階躍響應曲線如圖4所示。

3.1 力傳感器模型辨識

針對圖4所示階躍響應曲線進行非線性擬合，得到該傳感器的辨識模型為

其中：ξ=0.188 3，ωn=85.821 5。

得到的階躍響應曲線如圖5所示，通過比較擬合前后的曲線可以看出擬合后的曲線較好地體現出了傳感器的階躍響應動態特性。

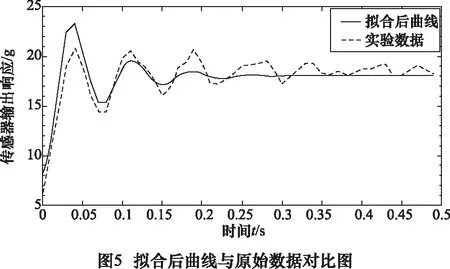
3.2 動態補償環節仿真設計與效果

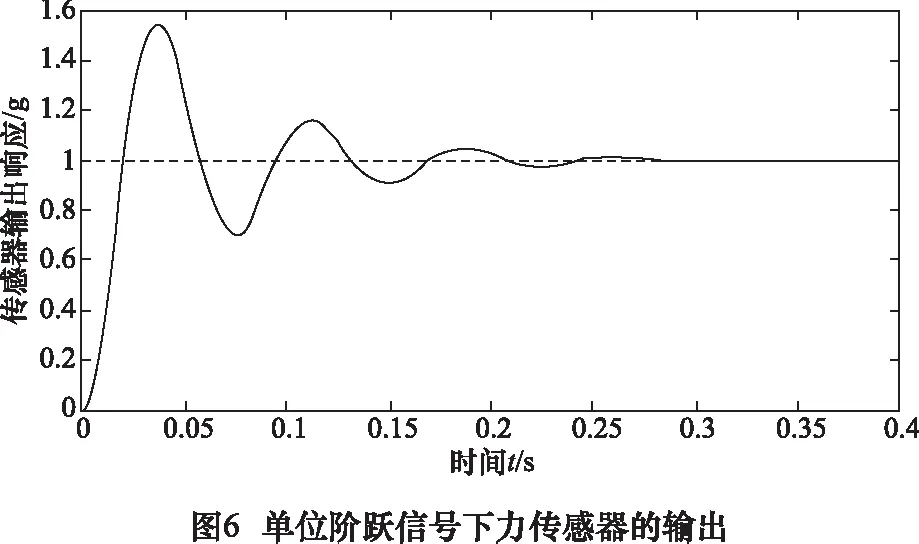
根據所得該傳感器辨識模型做出單位階躍信號下的力傳感器歸一化輸出曲線如圖6中可以看出該傳感器的動態特性較差，上升時間tr=0.02 s，峰值時間tp=0.04 s，調節時間ts=0.2 s，超調量σ≈58%。

根據零極點配置法設計動態補償濾波器來對傳感器進行動態補償。設計的補償環節為

在傳感器后添加該補償環節，通過Matlab仿真得到補償后的單位階躍響應輸出曲線，如圖7所示。補償后上升時間tr=0.008 s，峰值時間tp=0.01 s，調節時間ts=0.05 s，超調量σ≈4%。

從表1可以看出該傳感器通過添加補償環節后其動態特性有顯著提高。

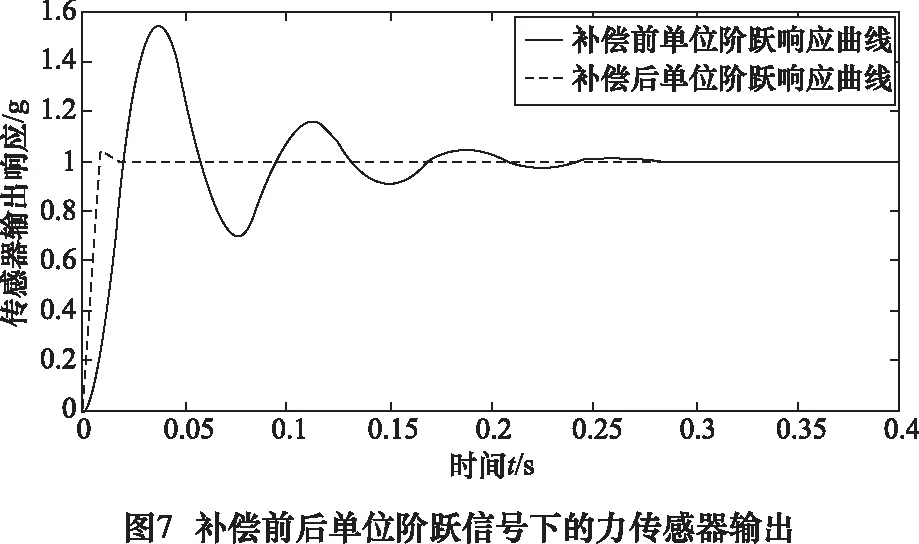
表1 補償前后單位階躍信號下動態特性比較

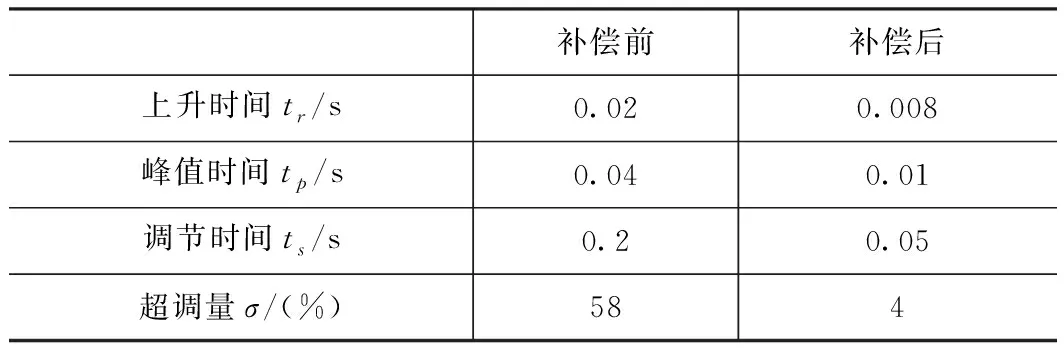
補償前補償后上升時間tr/s0.020.008峰值時間tp/s0.040.01調節時間ts/s0.20.05超調量σ/(%) 584

3.3 動態補償環節實驗設計

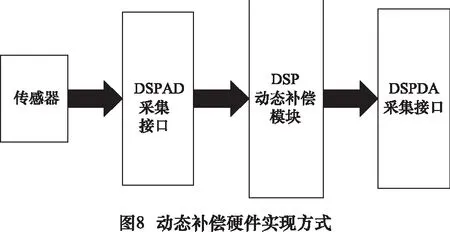
通過之前介紹的零極點配置法可以得到動態補償環節的離散傳遞函數。當被測信號不需要實時處理的情況下，可以采用軟件補償的方法實現動態補償器的設計，所有的數據處理在信號采集結束后由軟件進行，這樣可以節約額外的硬件成本，而動態補償環節也可以靈活設計。當被測信號需要實時處理使用時，就必須采用數值算法來實現動態補償數字濾波器的設計。數字濾波器的硬件設計可以使用數字信號處理器(簡稱DSP)來實現，采用這種方法可以獲得較快的數據處理速度，實現復雜的數字信號處理運算。具體實現方式如圖8所示。當傳感器對力檢測后產生信號經DSP的AD采集接口傳送到DSP中，經DSP編程設計動態補償模塊完成傳感器的動態補償環節，補償后的被測信號經DSP的DA采集接口傳出以實現實時處理的要求。

4 結語

本文針對力傳感器的動態特性進行了分析，研究了傳感器的系統建模和動態補償的問題。

根據力傳感器動態特性難以滿足實際要求，利用非線性最小二乘法比較切合實際地建立了傳感器的辨識模型，研究了零極點配置法設計了傳感器的動態補償環節的方法。最后通過實驗驗證了最小二乘法在建立非線性系統模型的可行性，并且證明了零極點配置法所設計的補償環節可以滿足對傳感器的使用要求，可以將該補償方法應用于工程實際當中。