基于APH的股票投資組合選擇研究

李夢辰

(重慶交通大學 經濟與管理學院，重慶 400074)

1 利用AHP法對股票投資組合選擇

1.1 建立遞階層次結構模型

充分分析股票信息相關的知識后，依據層次分析法的基本思想如下:

第一層:目標層。目標層是最高層，是決策問題的目標，本文即為“選擇股票”，本層由A代替。

第二層:準則層。包括實現目標的中間環節，根據引言中的分析，本次決策過程中的具體元素為主觀因素B、客觀因素B和宏觀因素B。

第三層:子準則層。根據分析，子準則元素具體為心里預期C、風險偏好C、人為操控C、公司運營C、股價C、市場利率C、行業情況C、通貨膨脹C、政治因素C、經濟政策C。

由此構造的股票層次結構，如圖1。

1.2 構造判斷矩陣

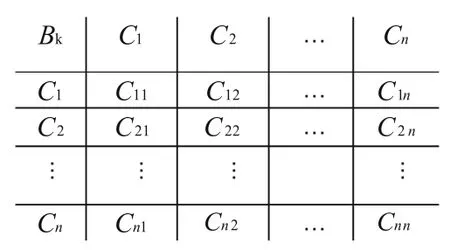
假定某一層次的元素B作為準則，對下一層元素有支配作用；我們在準則B下，根據下一層各元素之間兩兩的相對重要性賦予各元素一定權重數值。于是我們可以得到一個判斷矩陣C=(C)，也就是說C是權重值，表示因素i和因素j相對于準則B的重要值。判斷矩陣的一般形式如下:

在此原理基礎上，對于股票選擇模型，根據股票行業分析，我們可以得到以下矩陣:

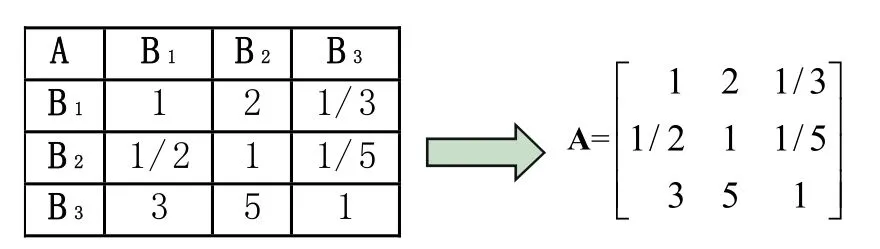
(1)準則層對目標層的判斷矩陣A-B(簡記為A):

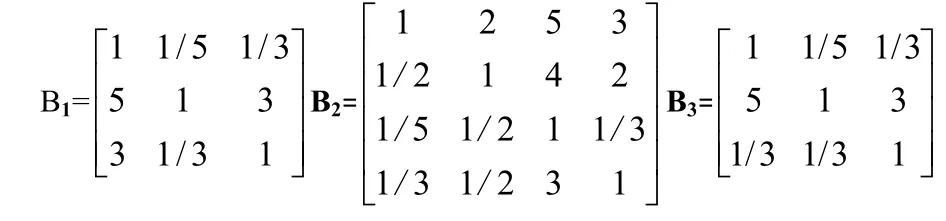
(2)同理，子準則層對準則層的判斷矩陣B、B、B為:

1.3 層次單排序和判斷矩陣一致性檢驗

建立判斷矩陣是為了計算單層次排序問題。然而在實際中，衡量兩元素的相對重要性時，各專家給的意見，會出現矛盾的情況，為避免評價結果失真，我們在計算權重的同時需要對判斷矩陣進行一致性檢驗。

根據理論計算公式，

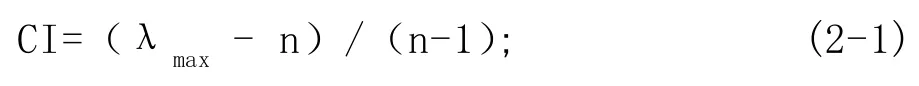
平均隨機一致性指標:

如果CR＜0.1，我們就認為判斷矩陣通過了一致性檢驗，否則需調整Cij的值，使其通過一致性檢驗。

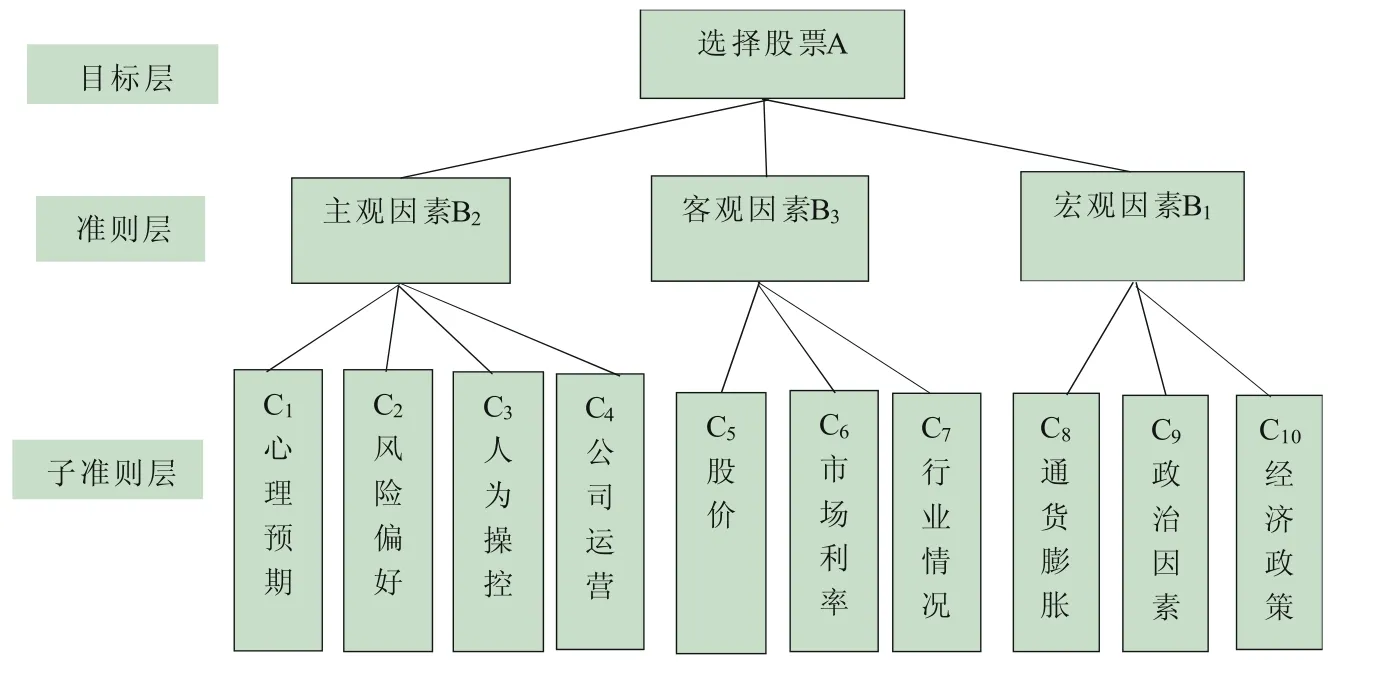
圖1 股票選擇需考慮的因素層次結構圖

求解單層次排序的權向量時，我們采取方根法。

在本例中，權向量的求解及一致性檢驗的計算結果，如表1。

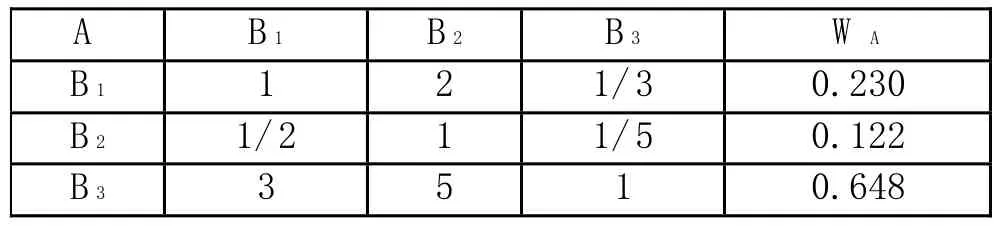
表1-1 判斷矩陣A-B的單層次排序

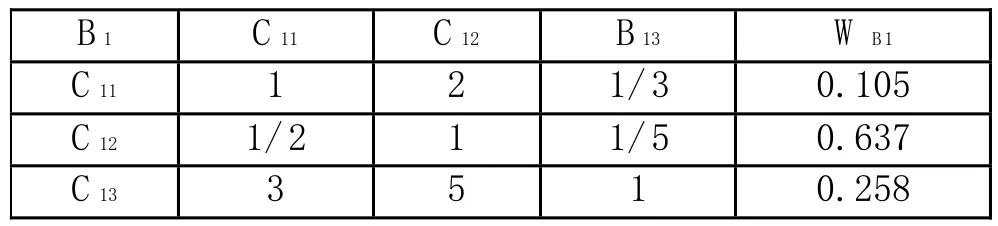
表1-2 判斷矩陣B1-C的單層次排序

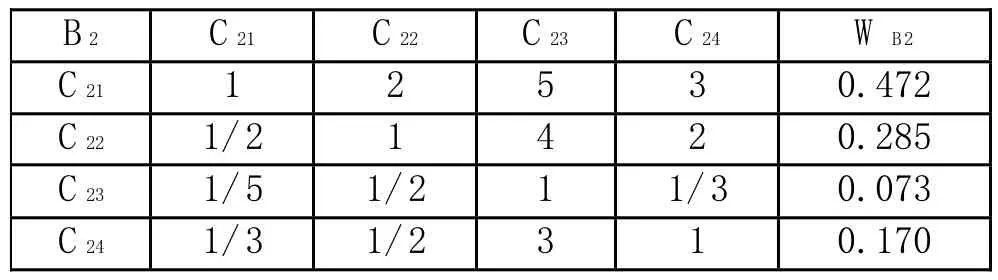
表1-3 判斷矩陣B2-C的單層次排序

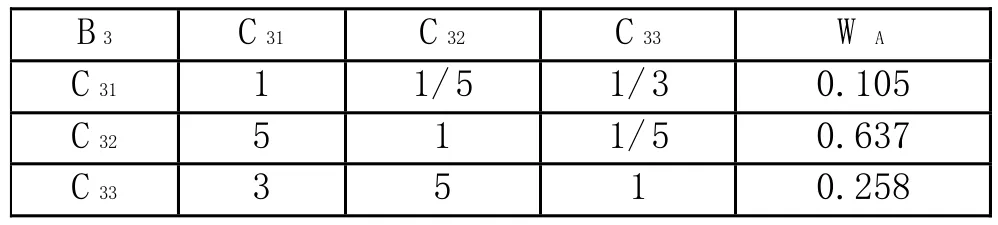
表1-4 判斷矩陣B3-C的單層次排序

1.4 層次總排序

因此，需要計算各層元素對系統目標的合成權重，進行總排序，以確定結構圖中最底層各個元素在總目標中的重要程度。這一過程是最高層次到最低層次逐層進行的。層次總排序的計算結果，如表2。

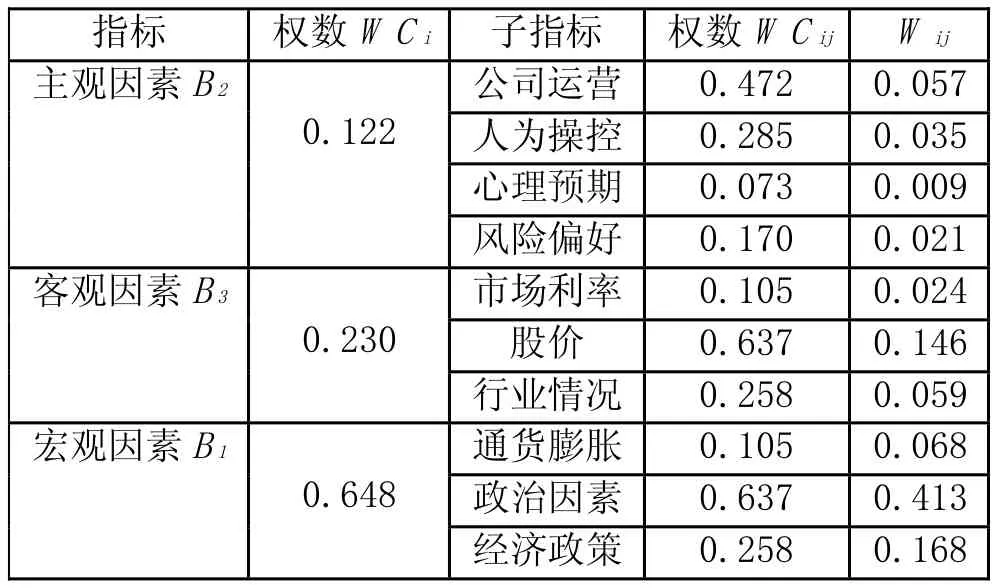
表2 股票選擇需考慮因素的層次總排序

1.5 股票投資組合選擇

對于股票投資者來說，在選擇股票時，可以利用層次分析法對股票選擇考慮的因素進行權重分析后，再根據行情數據來對各要素打分，通過對權重和得分的加權計算方法來對股票進行組合選擇，如表3。

1.5.1 單支股票計算

對三支股票:唯品會、王府井、深高速，給出得分，如表4。

加權后的總得分為:

(1)唯品會:

(2)王府井:

表3 平均隨機一致性指標(RI值)

表4 三支股票的得分情況

(3)深高速:

1.5.2 股票組合選優

馬科維茨在其文章中研究的股票投資組合原理就在此，其中驗證了證券投資市場中的古話:“不要把所有的雞蛋都放到一個籃子里”。

根據上述股票計算的數據，根據股票組合的比例和單只股票的總得分進行加權計算后。我們可以將股票組合為以下幾種情況:

單支股票類型:A，B，C；股票組合類型:AB，AC，BC，ABC，如表5。

表5 股票投資組合選擇

2 結語

根據以上計算結果，我們可以發現，單支股票的得分排序為:S＞S＞S；股票組合的得分排序為:S＞S＞S＞S；即單只股票投資應選唯品會，股票組合投資就應該選擇唯品會和深高速的組合(一個處于行業的上升發展期，另一個在行業中一直較為穩定，這樣組合的風險最小)。本文對于股票投資組合的論證可以總結為:(1)對于處于行業中發展勢頭好的行業，投資盈利性高，因此相比股票的穩定性更在乎收益的投資者可以選擇此類股票單獨投資；(2)對于股票組合投資來說，選擇一支收益高且穩定的股票是最理智的投資選擇，既能規避風險，而且能獲得可觀的收益(如組合AC)；(3)在選擇股票組合時，比例的確定可以采取的方法:收益高＞穩定性好＞收益低；

當然，本次對于股票組合的選擇研究只是基于層次分析法確定的各個影響因素的權重，對于各因素的得分是根據行情分析，組合比例的確定偏主觀，選優結果不夠完善；所以，在不同的行情下，需要更加科學的組合比例確定原則進行分析選擇最優組合。