基于唯一標識符的小范圍均衡隨機抽取方法

陳慶榮，陳明哲

（1.西安航空學院計算機學院，陜西西安710077；2.西安電子工程研究所陜西西安710100）

隨著信息技術的快速發展，計算機技術在各方面的應用日趨廣泛，各類應用系統在生產運營中起到了至關重要的作用，在這些應用系統中大量存在需要對候選數據進行隨機抽取的操作。這些應用系統在進行隨機抽取操作的設計時大多采用直接使用某種隨機函數對候選數據進行抽取的方法[1]，這種對候選數據隨機抽取的解決方法在候選數據量較大時基本可以保證抽取數據的均衡性，即每個候選數被抽中的次數基本相等。但是，當候選數據量較小時，使用這種方法進行候選數據的隨機抽取會導致數據抽取的不均衡，即在候選數較少時某些候選數被多次抽中，而其他候選數沒有被抽中或抽中次數較少的情況[2]。

本文通過對隨機抽取方法的研究和分析，在進行小范圍候選數隨機抽取問題中提出了一種基于唯一標識符的小范圍均衡抽取方法并加以實現，從而提高了小范圍候選數隨機抽取中抽取的均衡性并對此方法均衡性進行了分析測試。

1 基于唯一標識符的小范圍均衡隨機抽取方法

1.1 直接隨機抽取方法

方法的數理邏輯描述如下：

則f為由H到G的函數，并記作

f:H→G。

抽取方法說明：有n（n＜100）個候選數據的集合H，要隨機抽取其中的m（0＜m＜n）個數據生成結果集G，給集合H中的n個候選數據隨機生成唯一標識符nid，從中取出前m個候選數生成結果集G。

1.2 基于唯一標識符的小范圍均衡隨機抽取方法

方法的數理邏輯描述如下：

定義

候選集H={h1，h2，…，hn}，

均衡系數η（0＜η＜1），

均衡抽取數s（0＜s＜m），

抽取唯一標識符集W={＜w1，w2，…，ws＞|w1，w2，…，ws∈H}，唯一標識符抽取函數f1是由有序偶組成的集。f1的定義域 dom（f1）是集

dom（f1）=H；

函數f1的值域 ran（f1）是集

ran（f1）=W；

則f1為由H到W的函數，并記作

f1:H→W。

定義

已抽數據記錄集Y={＜y1，y2，…，yx|y1，y2，…，yx∈H}，已抽記錄集抽取函數f2是由有序偶組成的集。f2的定義域dom（f2）是集

dom（f2）=H；

函數f2的值域 ran（f2）是集

ran（f2）=Y；

則f2為由H到Y的函數，并記作

f2:H→Y。

定義

抽取中間集Z={z1，z2，…，zi|z1，z2，…，zi∈H并且z1，z2，…，zi?W}（i=m-s），抽取中間集函數f3是由有序偶組成的集。f3的定義域dom（f3）是集

dom（f3）=W-Y；

函數f3的值域 ran（f3）是集

ran（f3）=Z；

則f3為由H到Y的函數，并記作

f3:（W-H）→Z

定義

抽取結果集G={g1，g2，…，gm}，其中m＜n，則有G=W∪Z。

抽取方法說明：有n（n＜100）個候選數據的集合H，要隨機抽取其中的m（0＜m＜n）個數據生成結果集G；首先設置均衡系數η（0＜η＜1）和均衡抽取數s（0＜s＜m），給集合H中的n個候選數據隨機生成唯一標識符nid，并按此標識符排序，同時從中取出前s個候選數生成集合W，按照已抽取數據記錄集中抽取的數據已被抽取次數倒排序后生成已抽取數據記錄集Y，在集合Y中去除集合W中的所有元素并抽取前m-s個候選數生成抽取中間集合Z，最后抽取的結果集G為W∪Z。首次進行小范圍隨機抽取時只需設置均衡系數η=1，均衡收取數s=m，給集合H中的n個候選數據隨機生成唯一標識符nid，并按此標識符排倒序，同時從中取出前s個候選數即可生成抽取集合G。

2 方法測試

2.1 測試系統及方法

測試系統基于Java EE企業級開發標準設計和開發，采用面向對象的程序設計分別實現了直接隨機抽取和基于唯一標識符的小范圍均衡抽取。

為了對比在小范圍候選數中進行隨機抽取的效果，系統可以設置候選數個數、每次抽取候選數個數、抽取次數等信息，可以分別選用直接隨機抽取和基于唯一標識符的均衡抽取兩種抽取方法，后者抽取前系統還需設置均衡系數，抽取結果分別存入數據庫，并以圖表的形式統計顯示兩種抽取方法抽取的結果，從而可以比較直觀的對比兩種抽取方法的均衡性優劣。

2.2 方法測試及結果分析

2.2.1 測試1

系統設置50個候選數，每次抽取5個，連續抽取5次，分別使用直接隨機抽取方法和基于唯一標識符的小范圍均衡抽取方法，將使用兩種方法下被抽取的候選數進行統計并生成對應的統計圖及統計表，分別如圖1、表1、圖2、表2所示。

2.2.2 測試2

系統設置50個候選數，每次抽取10個，抽取5次，分別使用直接隨機抽取方法和基于唯一標識符的小范圍均衡抽取方法，將兩種方法下被抽取的候選數進行統計并生成統計圖及統計表，分別如圖3、表3、圖4、表4所示。

2.2.3 結果分析

在以上設置的兩種測試條件下，對相同測試數據按照直接隨機抽取的方法和基于唯一標識符的小范圍均衡隨機抽取的方法得到的抽取結果統計分析可以得到以下結果。

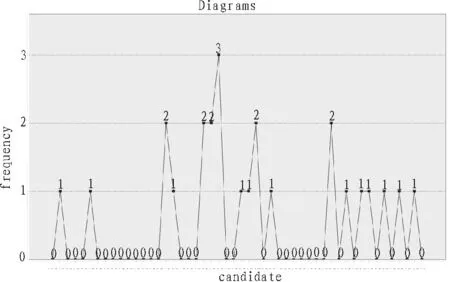
圖1 直接抽取結果統計圖

表1 直接抽取結果統計表

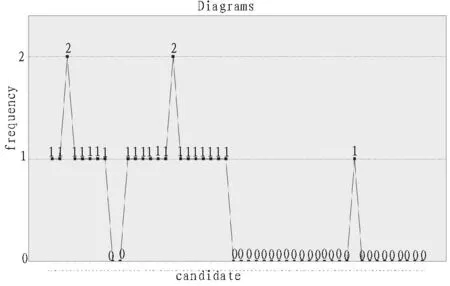
圖2 小范圍均衡隨機抽取結果統計圖

表2 小范圍均衡隨機抽取結果統計表

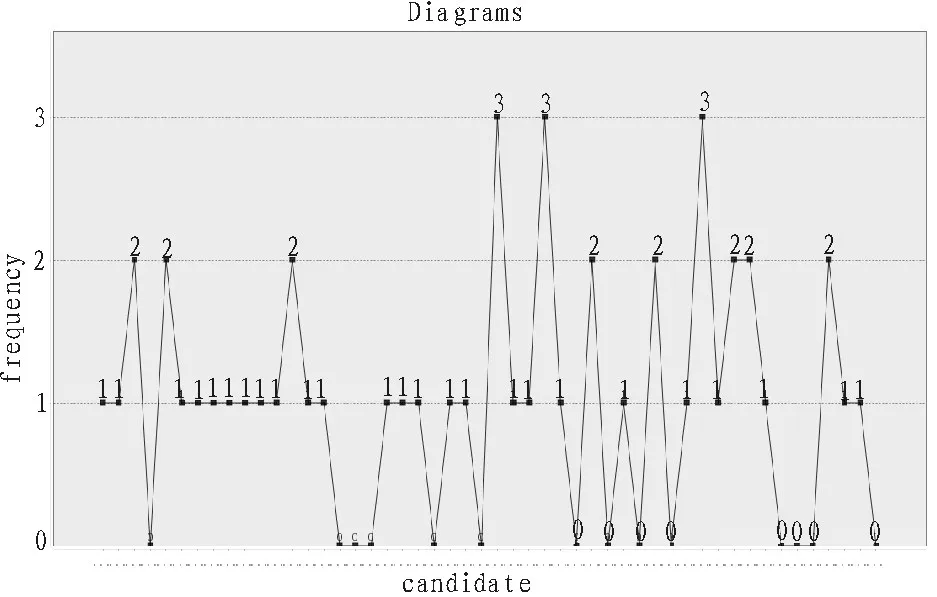
圖3 直接抽取結果統計圖

表3 直接抽取結果統計表

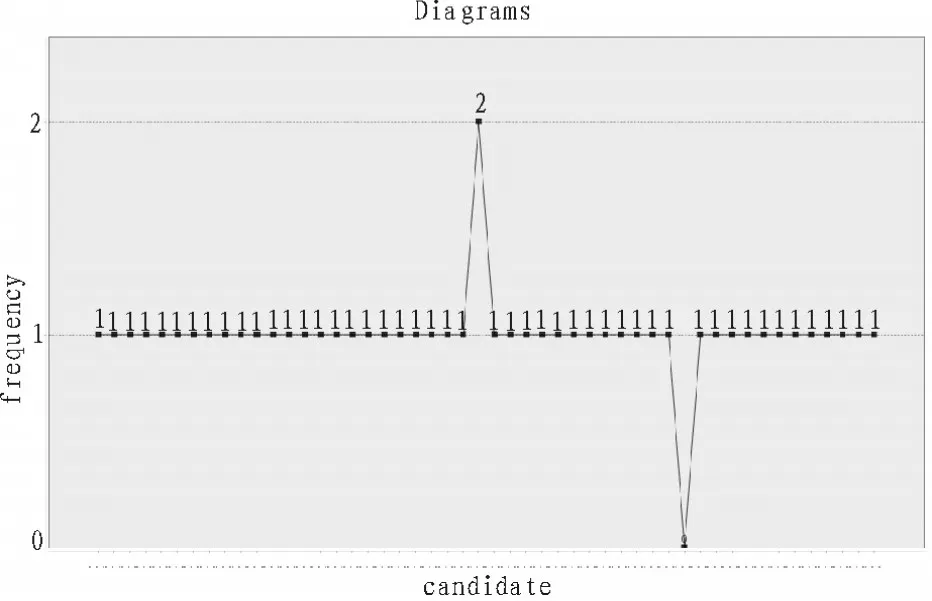
圖4 小范圍均衡隨機抽取結果統計圖

表4 小范圍均衡隨機抽取結果統計圖

測試1條件下，使用直接隨機抽取的方法，50個候選數，未被抽中的候選數占總候選數的64%，候選數被抽中的最高頻率為3。被抽中的25個候選數中，被抽取過1次的占48%，2次的占20%，3次的占4%。而基于唯一標識符的小范圍均衡隨機抽取方法，未被抽中的候選數占總候選數的54%，候選數被抽中的最高頻率為2，被抽中的25個候選數中，被抽取過1次的占84%，2次的占8%。從數據分析可以看出，直接隨機抽取方法未抽中的候選數和抽取的最高頻率要高于基于唯一標識符的小范圍均衡隨機抽取方法；而基于唯一標識符的小范圍隨機抽取方法下被抽取過1次的候選數多于直接隨機抽取方法。

測試2條件下，使用直接隨機抽取的方法，50個候選數，未被抽中的候選數占總候選數的28%，候選數被抽中的最高頻率為3，被抽中的50個候選數中，被抽取過1次的占50%，2次的占16%，3次的占6%。而基于唯一標識符的小范圍均衡隨機抽取方法，未被抽中的候選數占總候選數的2%，候選數被抽中的最高頻率為2，被抽中的50個候選數中，被抽取過1次的占96%，2次的占2%。依據數據分析，直接隨機抽取方法未抽中的候選數及抽取最高頻率均高于基于唯一標識符的小范圍均衡隨機抽取的方法；而基于唯一標識符的小范圍均衡隨機抽取方法下被抽取過1次的候選數則明顯多于直接隨機抽取方法。

通過對測試1和測試2條件下，按照設定的抽取范圍和抽取次數，使用直接隨機抽取的方法抽取結束后兩種測試情況下的數據分析均可看出候選數被抽中次數不均衡，且候選數中未被抽取到的情況較多；而通過對基于唯一標識符的小范圍均衡隨機抽取方法在兩種測試情況下數據分析，抽取結束后候選數被抽中的次數較直接隨機抽取均衡性改善很多，候選數未被抽到的情況大為減少，大部分候選數均可被抽到。

從實驗數據范圍、抽取次數及抽取結果的統計分析可以看出，在小范圍候選數隨機抽取時采用基于唯一標識符的均衡抽取方法得到的抽取結果的均衡性明顯優于直接隨機抽取的方法。同時在測試中，可以依據候選數的特點設置均衡系數以達到小范圍數據隨機抽取的均衡性達到在最優。

3 結束語

小范圍候選數隨機抽取是很多應用系統功能中需要實現的一項功能，直接使用各類隨機數的方法直接來處理小范圍數據的隨機抽取問題，會因候選數據量較小導致隨機數抽取均衡性較差，即就是某些候選數被抽中的次數明顯多于其他候選數，導致隨機抽取失去隨機意義。通過均衡測試系統的驗證可以看出：基于唯一標識符的小范圍均衡隨機抽取方法，利用設置均衡系數η及相關抽取集合依照此方法進行的相應變換，使得小范圍候選數隨機抽取的均衡性有了很大的改善，為小范圍數據隨機抽取提供了均衡性能良好的實用方法。