不同P2P網絡拓撲結構上進化博弈算法的研究

魯春蘭

（西安航空職業技術學院電子工程學院，陜西西安710089）

Peer，中文意思為，伙伴，同事。由Peer組成的網絡被稱為對等網絡，即Peer-to-Peer network[1]。P2P網絡是建立在IP網絡之上的應用層上的一種扁平化網絡，其憑借良好的可擴展性、健壯性、通信匿名性、流量均衡、組網簡單靈活等優勢，應用極為廣泛。P2P網絡應用極為廣泛，但仍然存在一些問題：“搭便車”現象[2]“洗白攻擊”[3]“公共悲劇”[4]。國內外學者針對P2P網絡的缺點，提出不同的模型來提升P2P網絡中節點的合作性，比如：文獻[5]將博弈論的觀點引入對等網絡中，文獻[6]通過博弈論的方法研究了網絡中節點的自私性，文獻[7-9]研究了在不同激勵下建立信任模型，文獻[10]給P2P網絡中的節點賦予一定信譽，節點根據其自身信譽享受不同的合作服務水平，文獻[11-13]提出了在網格網絡以及無標度網絡中，節點間更易于形成合作穩態。

1 進化博弈算法描述

網絡中的節點依次與自己的相鄰節點進行囚徒困境博弈，博弈完成后，當前節點從鄰居節點中選擇收益值最高的節點策略作為自己的策略，這是一種進化型博弈模型。網絡通過節點之間的動態演繹來激勵合作狀態的涌現。

文獻[14]中已經證明網絡節點被賦予一定的身份認證消息時，可以高效地遏制網絡中的“搭便車”行為，提高節點之間的合作性。該算法在P2P網絡里引入標兵節點，引導網絡里的節點選擇合作策略，另外，節點主動學習過程中根據收益差值選擇鄰居節點進行連接。通過仿真軟件的仿真已經證實了該算法的有效性和可靠性。

本文在文獻[14]的基礎上，將進化博弈算法進行了優化，并在兩種不同的P2P網絡上進行了仿真，仿真結果證明，在不同結構的P2P網絡中采取不同學習策略，網絡中節點的合作性均有很大提高。

2 近似網格P2P網絡上的進化博弈算法

為了抑制節點的自私性，Nowak等學者在網格網絡上運用斑型圖對囚徒困境展開了分析，發現網格網絡里采取合作策略的節點在網絡博弈過程匯總成簇，越聚越大，最后網絡中會出現合作穩態[15]。除了規則網格網絡外，還存在一種稀疏網格網絡。稀疏網格中有節點的缺失，缺失的節點位置可以一直保持空白，也可以連接到網絡中的其他節點上去。這樣的組網方式與P2P網絡形式十分類似，我們把這樣的稀疏網格網絡可以稱作近似網格P2P網絡。

本文的第一種進化博弈算法將在近似網格P2P網絡上模擬，近似網格P2P網絡由于其組網方式具有一定的規則性，其策略更新形式采用的選擇最優收益進化式。

弱囚徒困境與經典囚徒困境的區別在于收益矩陣參數設置的不同。從文獻[16]中可得出結論：弱囚徒困境與經典囚徒困境的演化結論是一致的。弱囚徒困境參數設置如下：R=1,T=1+r,P=S=0。其中，R＜T=1+r＜2R即0＜r＜1。r稱為背叛誘惑因子。進化博弈雙方的收益與收益矩陣有關，收益矩陣與背叛誘惑因子有關。因此，在計算節點收益，討論網絡中合作節點比例時必須從背叛誘惑因子入手。

3 改進型隨機P2P網絡上進化博弈算法

本文將構造一個類似無標度網絡的改進型隨機P2P網絡，這個隨機P2P網絡也有優先連接特性。雖然新構造的改進型隨機P2P網絡里每個節點擁有的相鄰節點數不一樣，但可以計算改進型隨機P2P網絡里每一個節點的平均相鄰的節點數，這個計算值是個固定的值。

改進型隨機P2P網絡中的每一個節點代表一個參與博弈的博弈者，節點之間的連線代表博弈者之間的信息交互。兩個節點相互博弈，博弈活動完成后計算本次博弈的收益值。接著進行節點策略的更新，節點依次選擇鄰居節點計算策略轉移概率p，接著系統產生一個隨機數，如果該隨機數的值小于策略轉移概率p，則節點會將自己的策略更新為相鄰節點的策略，策略更新過程完成。

改進型隨機P2P網絡由于其組網方式的隨機性，為了平衡組網方式的隨機性，在策略更新階段采取了策略轉移概率的更新方式。

策略轉移概率p的計算公式如下：

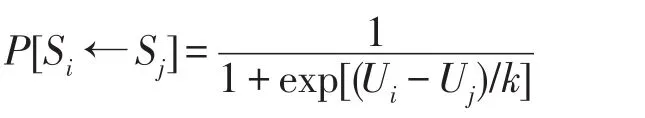
其中，Si，Sj分別表示節點i與節點j的策略，i表示當前節點，j表示相鄰節點。

4 仿真結果及分析

4.1 近似網格P2P網絡上的進化博弈算法參數配置

仿真實驗是在N*N=200*200的稀疏網格網絡上完成的。初始化網絡中的合作節點為30%，不合作節點為70%，進化博弈算法運行100個周期。背叛誘惑因子的取值區間為0＜r＜1。

4.2 近似網格P2P網絡上的進化博弈算法數據分析

實驗中，令背叛因子的取值分別為r=0.05，0.25，0.45，0.65，0.85，討論不同背叛因子對網絡合作演化的作用。

圖1中（a）～（e）圖，分別表示的是當背叛因子r=0.05，0.25，0.45，0.65，0.85時，網絡中合作節點與不合作節點的變化趨勢。對比可知，r=0.85不適合充當背叛誘惑因子。

下面主要研究在近似網格P2P網絡中，背叛誘惑因子的上限值。首先適當地減小背叛誘惑因子r的取值，定義r=0.8。圖2表示背叛誘惑因子r=0.8時，合作節點與不合作節點所占比例變化趨勢。從圖中可以看出，不合作節點所占比例一直高于合作節點所占比例，網絡在達到穩態之后，一直不會出現合作狀態。因此，r=0.8不是所求背叛誘惑因子的上限。

實驗中，又分別取了r=0.75，0.77，0.79來估算背叛誘惑因子的上限。圖3、圖4、圖5分別表示r=0.75，0.77，0.79時，偏向合作態度的節點與選擇不合作態度的節點所占比例變化趨勢以及模擬過程中的動態演化過程圖。

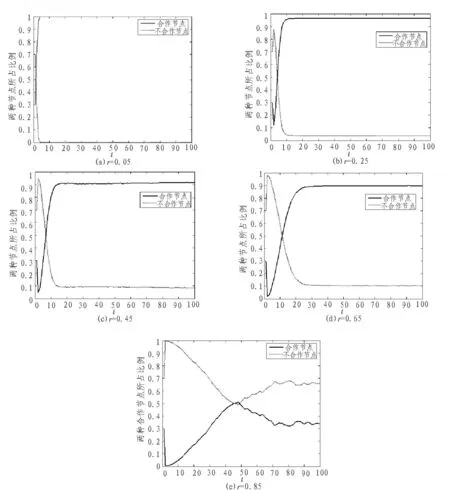
圖1 不同背叛誘惑因子下，合作節點與不合作節點所占比例變化趨勢

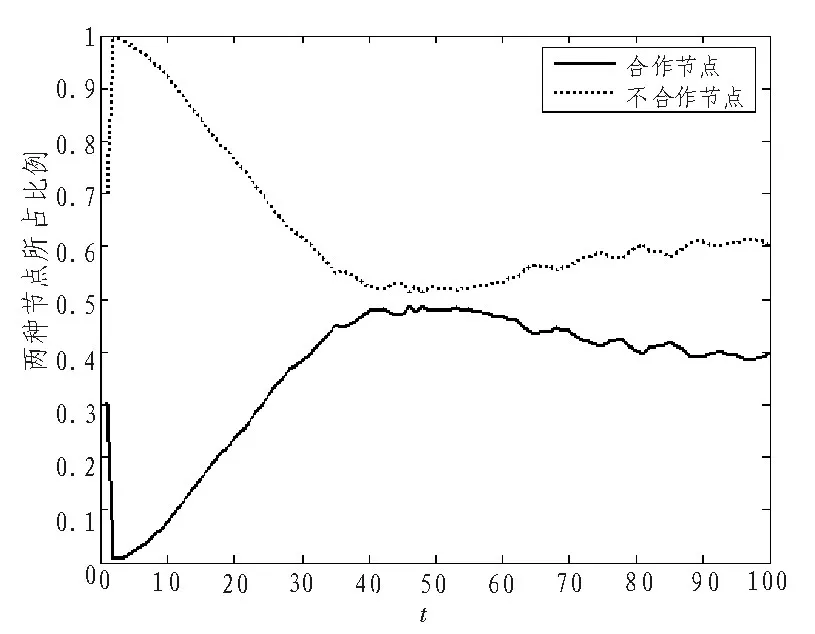
圖2 背叛誘惑因子r=0.8時，合作節點與不合作節點所占比例變化趨勢

對比這3組圖，我們對出現合作穩態最快的圖5進行分析。當背叛誘惑因子r=0.79時，從圖5中（a）可以看出，模擬進行到第70周期時，網絡就已經進入合作的穩定狀態。網絡在T0=42時，網絡里有數量相等的兩種節點。T=3時，合作節點處于變化曲線的波谷，對比動態演變過程，可以看到此時網絡中不合作節點處于統治地位，隨著模擬的不斷進行，網絡中出現了大量的合作節點形成的合作簇，逐漸擴展到不合作節點區域，最后整個網絡處于合作穩定狀態。

本文前面，通過模擬實驗已經得出：背叛誘惑因子r=0.8不是所求背叛誘惑因子的上限。而當背叛誘惑因子r=0.79時，網絡處于穩定的合作狀態。因此，定性分析背叛誘惑因子r=0.79是背叛誘惑因子的上限。背叛誘惑因子的取值范圍0＜r＜0.79。當背叛誘惑因子的值在本文所求解的取值范圍內，近似網格P2P網絡中就可以出現合作穩態。模擬證明，在近似網格P2P網絡中采取策略更新擇最優收益進化博弈算法可以使得網絡中出現合作穩態。

圖3 當背叛誘惑因子r=0.75時，圖（a）表示合作節點與不合作節點所占比例變化趨勢。圖（b）～（f）分別表示的是模擬周期[T]為0、5、30、60、100時的動態演化過程。其中淺色表示不合作節點，深色表示合作節點。

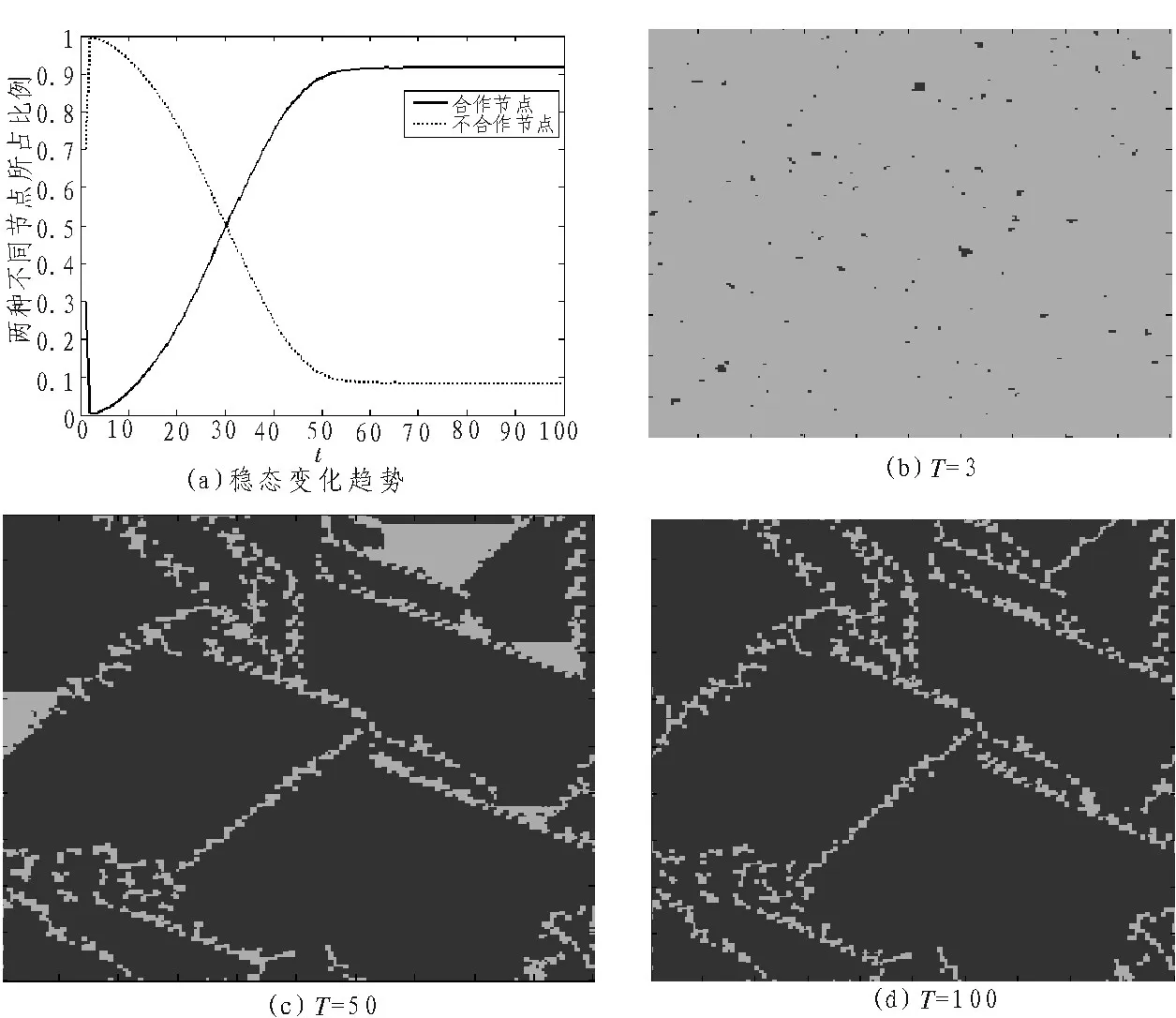
圖4 當背叛誘惑因子r=0.77時，圖（a）表示合作節點與不合作節點所占比例變化趨勢。圖（b）～（d）分別表示的是模擬周期T為3、50、100時的動態演化過程。其中淺色表示不合作節點，深色表示合作節點。

4.3 改進型隨機P2P網絡上進化博弈算法的研究

模擬實驗運行的環境為改進型隨機P2P網絡，為了體現對節點策略的公平性，并促使網絡中快速出現合作穩態，以下的實驗將在初始合作節點為50%的環境中進行。

當設置背叛誘惑因子r的值為0.06時，網絡中并未出現合作穩態。重新設置背叛誘惑因子的值，分別設置為0.99和0.1，初始化網絡中合作節點為50%。實驗運行100周期，結果如圖6所示。

圖5 當背叛誘惑因子r=0.79時，圖（a）表示合作節點與不合作節點所占比例變化趨勢。圖（b）～（f）分別表示的是模擬周期T為3、50、70、80、100時的動態演化過程。其中淺色表示不合作節點，深色表示合作節點。

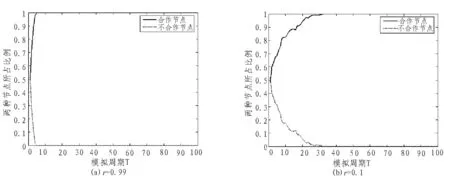
圖6 初始化網絡中合作節點為50%，圖（a）是背叛誘惑因子r=0.99時，兩種節點所占比例變化趨勢，圖（b）是背叛誘惑因子r=0.1時，兩種節點所占比例變化趨勢圖。

當背叛誘惑因子為0.99和0.1時，模擬運行結束時兩種狀態的網絡均達到了合作穩態。誘惑因子為0.99時，實驗運行到第5周期網絡已經達到了合作穩態，而r=0.1時的合作穩態則出現的稍微晚些，但也在第30周期出現合作穩態。由此可見，在隨機P2P網絡中，背叛誘惑因子越大，網絡中出現合作穩態時間越短，網絡越穩定。

接著，實驗對背叛誘惑因子分別取值為0.07，0.065，0.063和0.061，模擬運行100周期，結果如圖7所示。

由圖7可以看出，這4種不同大小的背叛誘惑因子下，合作節點所占比例逐漸增長，網絡中出現合作穩態。隨著背叛誘惑因子的不斷減小，合作穩態的穩固程度也依次減弱。

由于改進型隨機P2P網絡是一種完全隨機的網絡，節點之間博弈算法使用的收益矩陣是一種弱博弈矩陣，并且節點更新策略使用的是一種動態轉移概率策略，該概率中加入了非理性選擇的噪聲，背叛誘惑因子越小，競爭因素相對也就越少，因此，這種網絡情況下，網絡中的合作穩態出現的較晚。相反，背叛誘惑因子越大，節點之間的競爭越激烈，節點更愿意選擇合作策略，提高了網絡中節點的整體收益，良好的整體收益更深入地促進了網絡中合作穩態的出現。結合實驗數據，得出背叛誘惑因子的取值范圍為0.06＜r＜1時，改進型隨機P2P網絡中會出現合作穩態，并且背叛誘惑因子越大，合作穩態出現的越早越牢固。

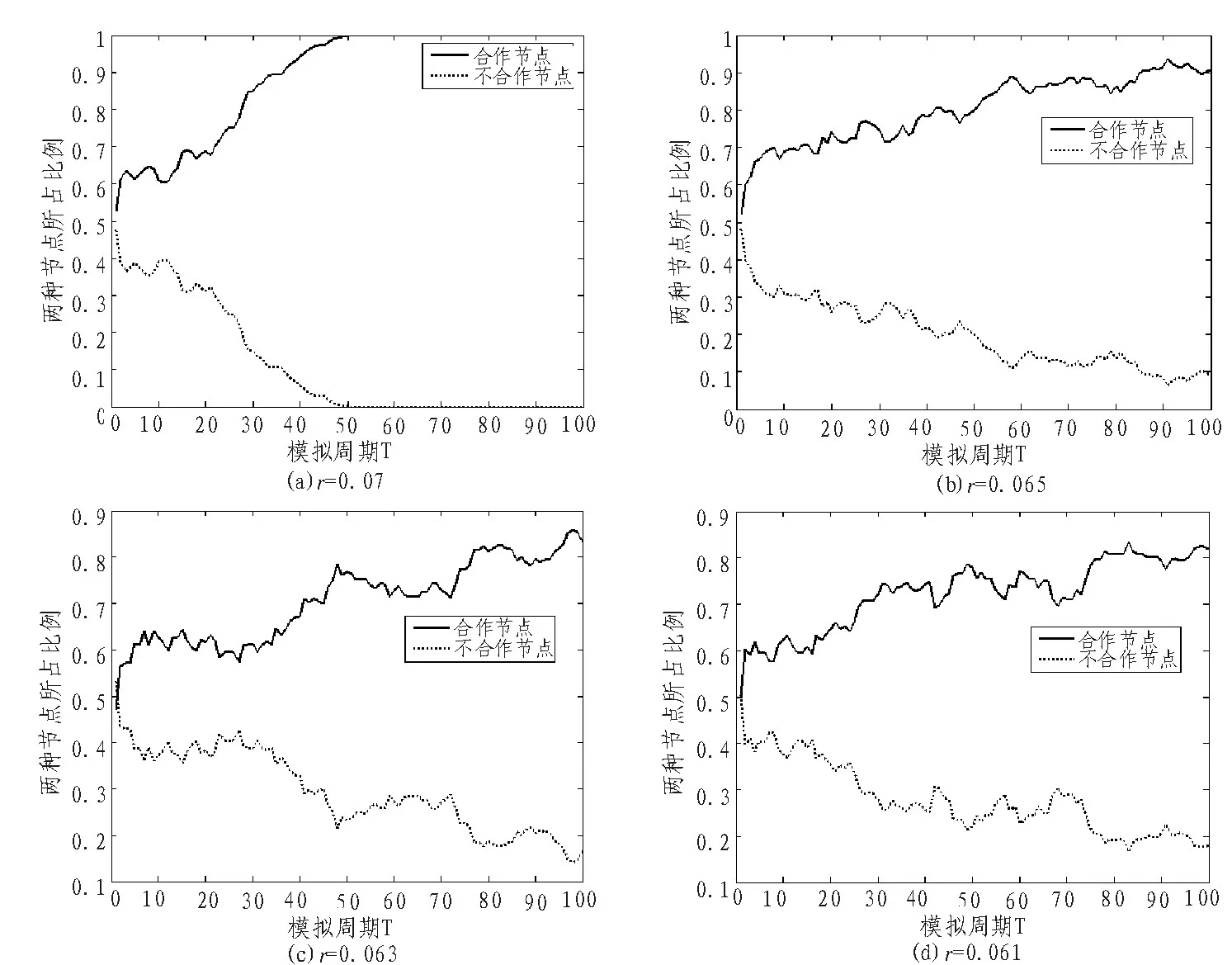
圖7 圖（a）～（d）分別是背叛誘惑因子為0.07，0.065，0.063，0.061時，網絡中兩種節點所占比例變化趨勢

5 結束語

為了促進P2P網絡中節點的合作性，本文分別在近似網格P2P網絡中模擬了選擇最優策略的進化博弈算法、在改進型P2P網絡中模擬了選擇概率轉移策略的進化博弈算法。仿真結果證明，在這兩種不同的拓撲結構中進化博弈算法均能促進網絡中合作穩態的出現。