變量有誤差的半?yún)?shù)模型的經(jīng)驗(yàn)似然推斷

劉 彭，張 超，柳平增

（山東農(nóng)業(yè)大學(xué)a.應(yīng)用統(tǒng)計(jì)與農(nóng)業(yè)信息化實(shí)驗(yàn)室；b.大數(shù)據(jù)中心，山東 泰安 271000）

0 引言

經(jīng)驗(yàn)似然方法是Owen[1]在1988年提出的一種非參數(shù)統(tǒng)計(jì)推斷方法，這種方法具有很多優(yōu)點(diǎn)：可以完全根據(jù)數(shù)據(jù)來(lái)決定變量對(duì)應(yīng)的置信區(qū)間，便于將多元數(shù)據(jù)進(jìn)行組合，還可以合并偏度信息，使得刪失數(shù)據(jù)或缺失數(shù)據(jù)的樣本更易于處理，具有糾偏性、無(wú)需構(gòu)造統(tǒng)計(jì)量等。因此，經(jīng)驗(yàn)似然方法在半?yún)?shù)回歸模型的各個(gè)領(lǐng)域應(yīng)用廣泛。

半?yún)?shù)回歸模型既含有參數(shù)分量，又含有非參數(shù)分量，結(jié)合了線性回歸模型和非參數(shù)回歸模型的優(yōu)點(diǎn)，因此不論是在理論研究上，還是在實(shí)際應(yīng)用中都具有重要意義。經(jīng)驗(yàn)似然方法已大量應(yīng)用于半?yún)?shù)回歸模型中，本文考慮變系數(shù)部分線性模型：

對(duì)于模型（1）的經(jīng)驗(yàn)似然推斷已有了大量的研究，如Hu[2]在2009年對(duì)變量有誤差的變系數(shù)部分線性模型進(jìn)行了研究，在兩種不同的情況下，提出了參數(shù)部分經(jīng)驗(yàn)對(duì)數(shù)似然比，構(gòu)造了參數(shù)部分的置信區(qū)間，Huang[3]在2009年對(duì)模型（1）利用經(jīng)驗(yàn)對(duì)數(shù)似然方法構(gòu)造了非參數(shù)部分的置信區(qū)間，同時(shí)得到了估計(jì)的經(jīng)驗(yàn)似然比服從標(biāo)準(zhǔn)卡方分布。本文針對(duì)變量有測(cè)量誤差的變系數(shù)部分線性模型，提出了非參數(shù)部分的經(jīng)驗(yàn)似然，并用對(duì)數(shù)似然法構(gòu)造了非參數(shù)部分的置信區(qū)間，證明了估計(jì)的經(jīng)驗(yàn)似然比服從標(biāo)準(zhǔn)卡方分布：

其中Eη=0,Eη2=Ση,且η與( )X,Z,U,ε獨(dú)立。

1 估計(jì)的經(jīng)驗(yàn)似然

為了定義經(jīng)驗(yàn)似然估計(jì)量，先假設(shè)β已知，可以利用約束，其中f(u)為U的密度函數(shù)，并有一個(gè)緊支撐S(f)。由此，引入如下輔助隨機(jī)向量：

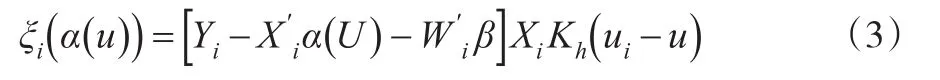
其中h是帶寬，Kh(·)=h-1K(·h)且K(·)是核函數(shù)。

如果β已知，由于是獨(dú)立的且，則可以構(gòu)造估計(jì)方程，此方程的解為α(u)的最小二乘估計(jì)，同樣可以通過(guò)經(jīng)驗(yàn)似然方法得到，因此，下面定義剖面經(jīng)驗(yàn)對(duì)數(shù)似然比函數(shù)：

若α(u)為真參數(shù)，則 ?n(α(u) )服從自由度為p的標(biāo)準(zhǔn)χ2分布，但是這里β未知，要對(duì) ?n(α(u) )進(jìn)行分析，比較可行的方法就是用估計(jì)量β?來(lái)代替β，下面就來(lái)估計(jì)β：

對(duì)l=1,…,p用kl個(gè)基函數(shù)的線性組合來(lái)逼近變系數(shù)函數(shù)為kl×1基函數(shù)向量，為kl×1未知函數(shù)向量，此方法的優(yōu)點(diǎn)在于：kl可任意增大，從而存在的線性組合很好地逼近任何光滑函數(shù)αl(U)，故其逼近的均方誤差可任意小。

定義K×1階矩陣逼近，此時(shí)，式（2）等價(jià)于：

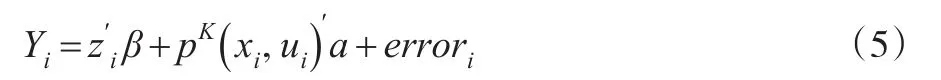
令：

又式（2）可以寫(xiě)成矩陣形式：

下面用修正的最小二乘法估計(jì)：

即得到估計(jì)量：

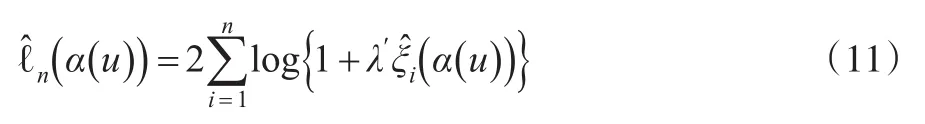
其中λ滿足：

若α(u)為真參數(shù)，則分布，要得到這個(gè)結(jié)論，下面先給出一個(gè)定義和一些條件：

定義1：?是一個(gè)函數(shù)類，如果?中任一函數(shù)g(x,z)滿足：

上述定義的詳細(xì)介紹參考文獻(xiàn)[4]。

條件1：u的密度函數(shù)f(u)有緊支撐S(f)，對(duì)所有l(wèi),k=1,…,p，γl,k(u),f(u)在u0處有連續(xù)一階導(dǎo)，對(duì)每個(gè)r=1,…,p，αr(u)在u0處的二階導(dǎo)數(shù)為連續(xù)有界函數(shù)；

條件2：核函數(shù)K(u)為有界對(duì)稱密度函數(shù)，其導(dǎo)數(shù)有界，且滿足

條件 3：存在τ＞1，使得

條件6：①對(duì)每個(gè)K，存在非奇異陣B，使得的最小特征值在K上一致有界大于 0；②存在滿足和K=Kn的序列ζ0(K),使得,其中S是(x1,u1)的支集。

定理1：在條件1至條件7下，且滿足h→0,nh3→∞,nh8→0, 若α(u0)為 真 參 數(shù) ，那 么

根據(jù)定理1，α(u0)的置信區(qū)間可以由式（10）構(gòu)造，對(duì)任意的的置信區(qū)間。

2 部分剖面經(jīng)驗(yàn)似然比

為了構(gòu)造α(u)的分片置信區(qū)間，這里借助部分剖面經(jīng)驗(yàn)似然方法來(lái)定義αr(u)的經(jīng)驗(yàn)對(duì)數(shù)似然比函數(shù)：考慮估計(jì)方程，這里er是第r個(gè)元素為1，其余元素為0的p維向量，α?(·)為的最小值，這里假設(shè)Q(u)可逆，對(duì)任意的h，聯(lián)合式（11）得：

其中，α?(u)等價(jià)于最小二乘估計(jì)，具體參考文獻(xiàn)[5]。

對(duì)數(shù)似然比函數(shù)為：

從定理2可將αr(u0)的置信區(qū)間定義為：

3 主要結(jié)果的證明

根據(jù)大數(shù)定律有：

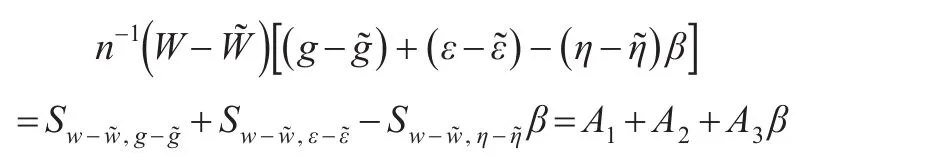
下面逐項(xiàng)證明：

其中：

顯然結(jié)論得證。

引理2：在定理1的條件下，如果α(u0)是真參數(shù)，則有

這里僅證A4,A5，其他的類似可以得到。

對(duì)任意的δ＞0，

故A4=op(nh)12,A5=op(nh)12，即結(jié)論成立。

引理3：在定理1的條件下，如果α(u0)是真參數(shù)，那么：

引理4：在定理1的條件下，如果α(u0)是真參數(shù)，那么：

引理5：在定理1的條件下，如果α(u0)是真參數(shù)，則,其中λ在式（12）中定義。

引理3、4、5的證明參考文獻(xiàn)[2],這里不再詳述。

定理1的證明：結(jié)合引理，對(duì)式（11）利用Taylor展開(kāi)式得：

根據(jù)式（12）可以得到：

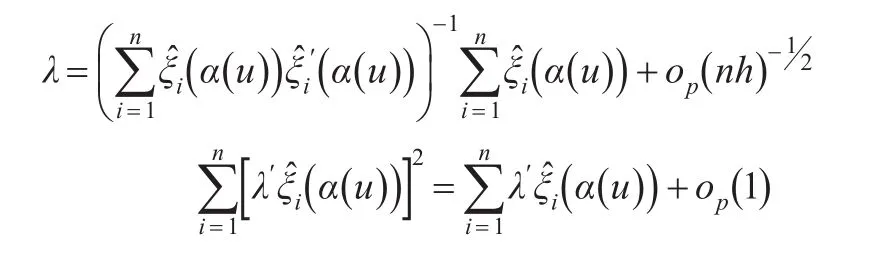
由上面三個(gè)式子定理1易證。

定理2的證明參考文獻(xiàn)[6]。

4 結(jié)束語(yǔ)

本文介紹了協(xié)變量有誤差的半?yún)?shù)變系數(shù)部分線性模型的似然推斷，提出了經(jīng)驗(yàn)似然在半?yún)?shù)誤差模型中的應(yīng)用。對(duì)于刪失數(shù)據(jù)、缺失數(shù)據(jù)在廣義線性模型、線型混合模型中的經(jīng)驗(yàn)似然推斷有所欠缺，還有待進(jìn)一步的研究。