基于聯合代數重建的電容層析成像圖像重建
宋亞杰, 張立峰, 朱炎峰
(華北電力大學 控制與計算機工程學院,河北 保定 071003)
0 引言
電容層析成像(Electrical Capacitance Tomography,ECT)技術是一種新型的多相流檢測技術[1]。其原理是通過安裝在管道外側的電極陣列采集數據,對管道內部介電常數分布進行實時可視化測量。ECT系統由于其非侵入、響應速度快、結構簡單、無輻射的特點,已在多相流領域逐漸得到應用[2,3]。
ECT圖像重建算法是一個逆問題求解的過程,但是逆問題具有非線性和病態性[4],而非線性和病態性都將直接影響圖像精度。目前常用的ECT重建算法可分為非迭代算法和迭代算法,非迭代算法如線性反投影算法(Linear Back Projection,LBP)雖然成像速度快,但很難取得較高精度的重建圖像;迭代算法成像精度明顯優于非迭代算法,如Landweber算法、Tikhonov正則化算法等,但一般收斂速度較慢[5]。
代數重建技術(Algebraic Reconstruction Technique,ART)是投影重建的典型方式之一,文獻[6]將ART算法應用在ECT圖像重建上,取得了較好的成像效果,但ART算法計算量大,重建速度較慢。聯合代數重建技術(Simultaneous Algebraic Reconstruction Technique,SART)是在ART算法基礎上改進而來,可有效克服逆問題的病態性和不適定性,不僅加快了迭代速度,重建圖像的質量也得到進一步提高,且具有一定的抗噪能力[7]。本文將SART算法應用于ECT圖像重建,采用16電極ECT系統,針對4種常見流型,分別使用ART算法和SART算法進行仿真并重建圖像,同時用成像效果、迭代次數、迭代時間和相對誤差等評價指標進行對比分析。最后,使用天津大學研制的數字化TJUET測量系統,模擬油/氣兩相流進行了靜態實驗,基于兩種算法得到重建圖像,并對比了分析測試結果。
1 理論基礎
1.1 ECT數學模型
ECT系統測量過程中,依次選擇其中一個電極作為激勵電極,其它電極作為測量電極用以獲取所有不同電極對之間的電容數據。由此可獲得獨立測量電容數據個數為:
M=K(K-1)/2
(1)
式中:K為電極數。本文使用16電極傳感器,因此將會得到120個獨立測量電容數據。
ECT系統中,被測圓形管道內部電場分布方程為:
·[ε(x,y)]φ(x,y)=0
(2)
式中:ε(x,y)為相對介電常數;φ(x,y)為電勢;φ(x,y)為電場強度。對式(1)進行離散化,即可得到ECT系統近似線性模型:
C=SG+e
(3)
式中:C為N×1維歸一化后的電容測量值;S為M×N維歸一化后的靈敏度系數矩陣;G為需要N×1維歸一化后的原始圖像灰度值向量;e是噪聲向量;N為剖分的網格數。獨立測量數據個數往往小于網格數,即M 代數重建算法[8]廣泛應用于圖像重建領域。該算法要求待重建的截面圖像f(x,y)分成N個離散的像素方格,而每個像素方格內部的f(x,y)都是常數,記作fi。然后,根據成像的物理過程和相應的數學模型,得到重建圖像和投影數據之間關系的線性方程組[9]。 (4) 式中:pi為第i號射線的測量數據;wij為反映像元fi對投影pi貢獻的權重因子;M為投影射線總數;N是像素方格個數;pi可視為歸一化的測量電容值;wij可認為是靈敏度矩陣單元;fi便是待重建的像素單元灰度值。觀察可知,式(4)可近似表示為ECT系統的線性模型方程(3),因此可用于ECT系統的圖像重建。圖像重建的任務即是由w、p求取f。 ART算法的具體步驟為: 步驟1:設定圖像初始值。初始值的設定將會直接影響到圖像重建迭代次數,一般情況下可設初始值如式(5);為提高重建速率,本文則以LBP算法得到的解作為初始值。 (5) 步驟2:根據下式計算圖像的修正值 (6) 式中:k為迭代次數;1≤i≤M;1≤j≤N;λ為松弛因子(0<λ<2)。為更好地抑制偽影,對于像元fi< 0,則使fi= 0。當所有的投影數據都被使用完,便完成了一次完整的迭代。 步驟3:反復進行第2步中的運算,對圖像進行修正。 步驟4:檢驗是否滿足收斂準則。常用的收斂標準是: (7) 當(U(k)N)1/2<ε(0<ε<1)時,停止迭代,也可設置迭代次數作為收斂停止條件。 作為ART算法的改進技術,SART算法仍然以式(4)為基礎進行改進。由上文可知,式(4)可近似表示為ECT系統的線性模型,因此SART算法克服了逆問題求解的非線性問題;在SART算法中,每次迭代對像素的校正值并非只與一個投影數據有關,而是所有投影數據校正值的平均值,一些隨機誤差被平均掉了,這也就使得SART算法能夠更好地抑制帶狀偽影,得到比ART算法更加平滑的重建圖像[10~12]。 SART算法的具體步驟為: 步驟1:設置圖像初始值(見ART算法第1步)。 步驟2:SART算法子迭代過程可分解為以下兩步: (8) (9) 步驟3:反復進行第2步中的運算,對圖像進行修正。 步驟4:檢驗是否滿足收斂準則(見ART算法第4步)。 仿真實驗平臺基于Windows8 Intel Core i7 2.60 GHz操作系統,內存為4 GB RAM;仿真軟件采用MATLAB R2009 a和COMSOL3.5 a有限元軟件。網格剖分采用自適應三角形網格剖分,圖像重建采用正方形網格剖分,將成像區域分為812個單元。采用16電極ECT系統,電極均勻排列在圓形管道外側,屏蔽罩和徑向屏蔽電極接地,用于屏蔽外界電磁干擾對測量信號的影響。其中電極張角θ=12°,管道內徑為80 mm,如圖1所示。 圖1 16電極ECT傳感器結構圖 仿真實驗以油/氣相流為研究對象,設置了如圖2所示4種常見流型。其中油和氣的相對介電常數分別設為3和1。使用COMSOL3.5 a有限元軟件獲得仿真測量電容值數據,并在此基礎上加入±2%的高斯白噪聲;利用MATLAB軟件編寫ART算法和SART算法完成ECT圖像重建。 圖像重建算法參數設置:為增加ART算法和SART算法重建效果的對比有效性,選取線性反投影算法(LBP)的重建結果作為重建算法的圖像初始值;迭代次數設置為150次;固定松弛因子λ=1。重建圖像如圖2所示。 圖2 仿真重建圖像 為定量評價重建圖像質量,采用相對誤差(IE)和相關系數(CC)作為評價標準。 (10) (11) 表2 重建圖像相關系數 由表1和表2可知,對所選4種常見流型,ART算法和SART算法的相對誤差和相關系數較為接近;結合圖2的重建圖像,不難發現SART算法能對不同物體有效地區分,且邊緣信息保真度高,具有較少的偽影。 流型1和流型2中,ART算法成像的物體略微變形,而SART算法成像的物體更接近原流型;此外可以看到,在ART算法重建圖像中,管壁部分存在偽影,而SART算法圖像中幾乎不存在;對于流型3的層流,兩者成像效果都不理想,尤其是靠近管壁的部分失真嚴重,相比較而言,SART算法的成像效果略好一些;而對于流型4的環流,如果不考慮偽影的存在,ART算法優于SART算法,成像更接近原流型。 表3為采用ART和SART的圖像重建耗時對比。 表3 圖像重建耗時 s 另外,由表3可以看出,對于4種常見流型,SART算法的成像時間最短。尤其對流型4,成像速度比ART算法快了接近一倍。 采用天津大學研制的數字化TJUET測量系統進行了靜態實驗,數字化TJUET系統如圖3所示。 圖3 數字化TJUET系統 兩相流模擬實驗中采用傳感器模型為內徑 60 mm的圓形有機玻璃管道,16電極電容敏感陣列。流型1’、流型2’和流型3’使用的是直徑分別為5 mm、10 mm、20 mm的塑料棒,而流型4’使用的是內徑30 mm、厚度2 mm的空心PC塑料棒,空場及滿場標定介質分別為空氣及塑料顆粒,管內剖分812個單元。實驗結果如圖4所示。 圖4 靜態實驗重建圖像 由圖4可知,對于流型1’和流型2’,ART算法成像的物體變形嚴重,且與管壁粘連,而SART算法成像邊緣信息保留較好,圖像更接近真實分布;對于流型3’的層流,兩者成像效果仍不理想,高介電物質呈離散分布;而對于流型4’的環流,兩種算法都取得了較好成像效果,相比較下,ART算法成像物體大小更接近原流型。 本文針對ECT圖像重建中逆問題的非線性和病態性,將基于ART算法的SART算法應用于ECT圖像重建。通過仿真和實驗測試顯示,ART算法和SART算法皆可有效地對物體進行重建,而SART算法的成像物體邊緣信息保真度高,且能抑制大部分偽影,具有一定的抗噪性能;另外,在成像效果相差不大的情況下,SART算法的成像速度要優于ART算法。該算法為解決ECT成像中的逆問題提供了一條新的途徑。1.2 代數重建算法(ART)
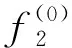
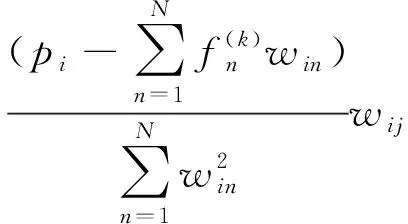
1.3 聯合代數重建算法(SART)
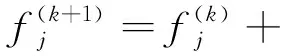
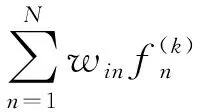
2 實驗結果及分析
2.1 仿真實驗

2.2 靜態實驗

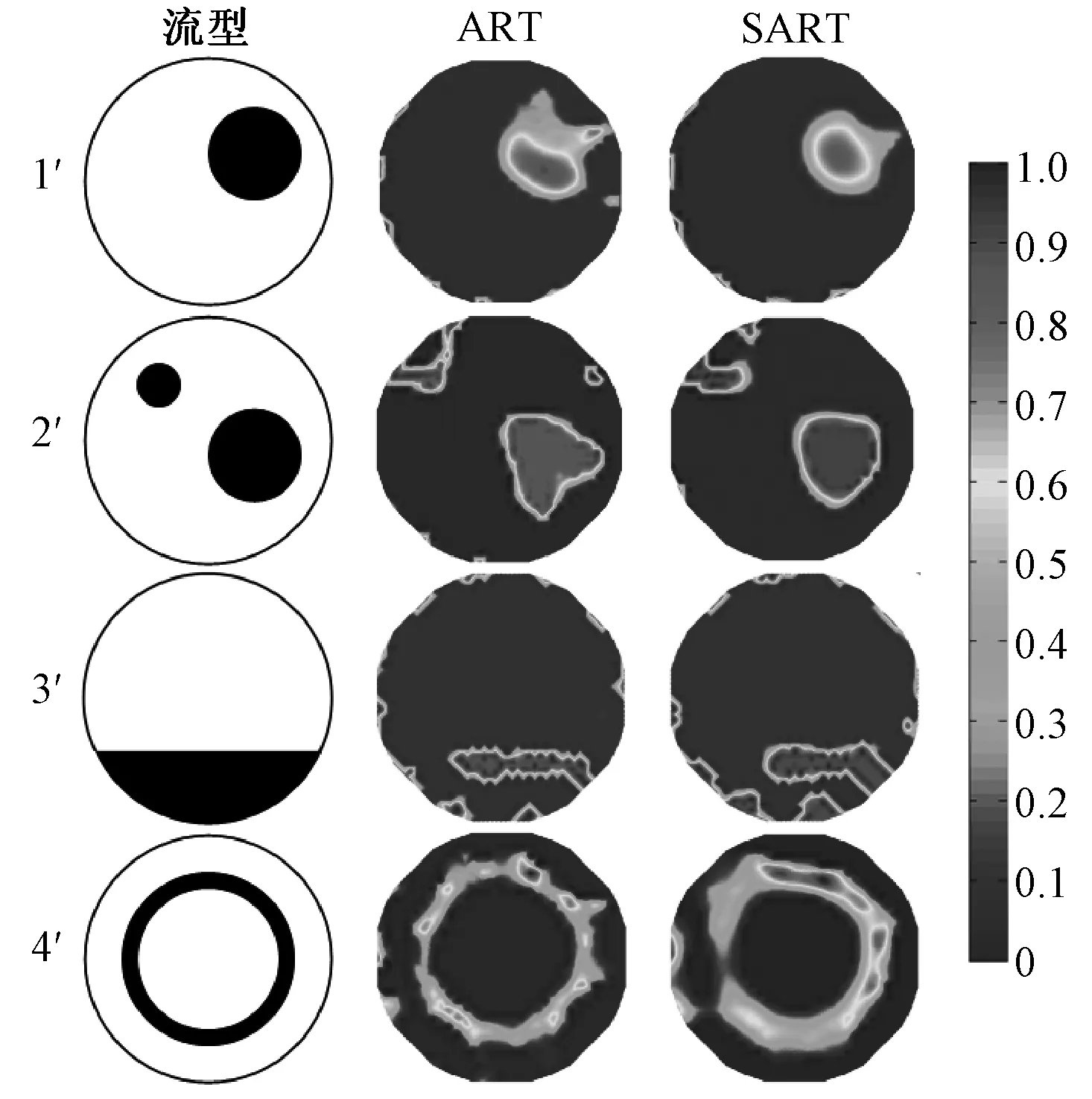
3 結論

