多相流耦合水擊模型在泄壓閥壓力精度設(shè)定中的應(yīng)用*

駱正山，鐘 強(qiáng)

(西安建筑科技大學(xué) 管理學(xué)院，陜西 西安 710055)

0 引言

多相流水擊產(chǎn)生的壓強(qiáng)是嚴(yán)重危害油氣管道系統(tǒng)安全運(yùn)行的重要因素，其變化情況及對(duì)應(yīng)的安全防護(hù)裝置-氮?dú)馐剿畵粜箟洪y的壓力精度，是提高油氣管道系統(tǒng)安全性的重要理論依據(jù)[1-4]。由于多相流水擊的作用過(guò)程比單相流更為復(fù)雜，因此，要準(zhǔn)確的計(jì)算出水擊壓強(qiáng)，需掌握多相流水擊所具有的特征及規(guī)律，提出更符合實(shí)際工況的理論計(jì)算方法。氮?dú)馐剿畵粜箟洪y作為有效應(yīng)對(duì)水擊問(wèn)題的重要保護(hù)裝置，對(duì)其進(jìn)行的研究也大多聚焦在泄壓閥的應(yīng)用維護(hù)和內(nèi)部流場(chǎng)變化情況等領(lǐng)域[5-7]。周云龍等[8-9]基于多相流體力學(xué)理論和數(shù)值方法，構(gòu)建了考慮含氣量變化多相流水擊模型，對(duì)含氣量變化條件下的氣液固三相流水擊問(wèn)題進(jìn)行了數(shù)值計(jì)算；Aldeeb等[10]構(gòu)建了當(dāng)氣液兩相流發(fā)生水擊時(shí)，模擬泄壓閥的動(dòng)態(tài)響應(yīng)過(guò)程和穩(wěn)定性變化情況的數(shù)學(xué)模型，同時(shí)通過(guò)實(shí)驗(yàn)得到在不穩(wěn)定條件下，來(lái)自不同制造商、不同型號(hào)的泄壓閥的動(dòng)態(tài)響應(yīng)數(shù)據(jù)，并根據(jù)實(shí)驗(yàn)數(shù)據(jù)對(duì)各類預(yù)測(cè)模型進(jìn)行了比較；李樹勛等[11-13]運(yùn)用浸入實(shí)體法與計(jì)算流體力學(xué)方法模擬氮?dú)馐剿畵粜箟洪y啟閉過(guò)程的流場(chǎng)變化情況，為泄壓閥的流道優(yōu)化及結(jié)構(gòu)改進(jìn)提供理論指導(dǎo)依據(jù)，構(gòu)建了模擬泄壓閥作用過(guò)程和泄壓閥組件受力情況的閥芯組件模態(tài)數(shù)學(xué)模型，閥芯組件預(yù)應(yīng)力模態(tài)數(shù)學(xué)模型，閥瓣運(yùn)動(dòng)模型以及閥芯運(yùn)動(dòng)力學(xué)模型；吳維等[14]基于動(dòng)力學(xué)理論，對(duì)液壓自由活塞的運(yùn)動(dòng)過(guò)程進(jìn)行了動(dòng)態(tài)分析。綜之，現(xiàn)有的多相流水擊問(wèn)題的研究在構(gòu)建油氣水多相流水擊模型等方面還不夠深入，較少有耦振對(duì)水擊壓強(qiáng)、水擊波速等數(shù)值變化問(wèn)題的研究；氮?dú)馐剿畵粜箟洪y的研究也大多聚焦于泄壓閥的安裝維護(hù)、流道優(yōu)化與結(jié)構(gòu)改進(jìn)等方面，現(xiàn)有的泄壓閥壓力精度設(shè)定方法的研究寥寥無(wú)幾。

為此，本文考慮了在水擊作用下管道耦合振動(dòng)對(duì)水擊壓強(qiáng)等數(shù)值的影響，構(gòu)建計(jì)算油氣水多相流水擊壓強(qiáng)的多相流耦合水擊模型，并將水擊模型應(yīng)用到氮?dú)馐剿畵粜箟洪y的壓力精度設(shè)定問(wèn)題中，為氮?dú)馐剿畵粜箟洪y的壓力精度設(shè)定問(wèn)題提供一定的理論指導(dǎo)。

1 水擊的產(chǎn)生及危害

管道閥門的突然關(guān)閉或者開啟，使管道內(nèi)原本高速流動(dòng)的流體發(fā)生流量突變或流速突變，由于流體的慣性造成管道內(nèi)壓強(qiáng)大幅度波動(dòng)的現(xiàn)象即為水擊現(xiàn)象。引起管道內(nèi)流體流量突變的因素主要分為2類：第1類是可控的，比如調(diào)整流量大小，切換輸送油品等；第2類是不可控的，比如輸送泵站突然停止工作，干線截?cái)嚅y門突然關(guān)閉等。以管道干線閥門突然關(guān)閉為例來(lái)說(shuō)明水擊產(chǎn)生的原因和作用過(guò)程。在有壓管道中，輸送介質(zhì)高速運(yùn)動(dòng)并附帶有較高的壓力，當(dāng)閥門突然關(guān)閉時(shí)，臨近閥門的一層流體首先停止運(yùn)動(dòng)，并被后續(xù)流體壓縮，壓力增高。此時(shí)，由于管道內(nèi)部壓力升高，管壁會(huì)發(fā)生局部膨脹，此后緊鄰的第二層流體由于受阻停止運(yùn)動(dòng)，發(fā)生同樣的變化。因此，管中流體壓力一層層的相繼增大及管壁相繼膨脹并以壓力波的形式由近及遠(yuǎn)傳播。一段時(shí)間后，壓力波傳至管道入口處，這時(shí)全管流體處于暫時(shí)靜止和被壓縮狀態(tài)，入口處的壓力歸零，而臨近出口閥門處的流體在壓差作用下，開始反沖向入口端，于是發(fā)生變化的部位首先恢復(fù)原來(lái)的狀態(tài)。如此反復(fù)的作用過(guò)程造成管線來(lái)回振蕩，對(duì)兩端的設(shè)備不斷造成沖擊，如果振蕩頻率和管線發(fā)生共振，其破壞力會(huì)增強(qiáng)，極易造成管道疲勞損壞，嚴(yán)重時(shí)發(fā)生油氣泄漏，引發(fā)事故。

2 原理及模型構(gòu)建

2.1 模型構(gòu)建基本原理

多相流水擊會(huì)使管道的線密度發(fā)生改變，嚴(yán)重時(shí)引發(fā)流體喘振，在流固耦合作用下，流體喘振會(huì)進(jìn)一步誘發(fā)管道產(chǎn)生劇烈振動(dòng)，從而使管道內(nèi)的流體壓強(qiáng)變化情況更加復(fù)雜多變。為了準(zhǔn)確計(jì)算流體壓強(qiáng)的變化情況，引入計(jì)算結(jié)構(gòu)力學(xué)理論，在構(gòu)建水擊模型時(shí)考慮流固耦合作用的影響，構(gòu)建油氣水三相流耦合水擊模型。安裝有氮?dú)馐剿畵粜箟洪y的輸油管道，在發(fā)生水擊問(wèn)題時(shí)，通過(guò)啟閉泄壓閥閥瓣等動(dòng)作，可將壓力進(jìn)行泄放，保障管道系統(tǒng)的安全性。通過(guò)對(duì)泄壓閥的受力情況進(jìn)行分析，可將作用在泄壓閥閥芯上的力主要分為多相流體作用力、氮?dú)鈮毫蛷椈闪Γ咧g相互作用，使泄壓閥閥芯可在泄壓閥殼體水平方向上做往復(fù)運(yùn)動(dòng)。由此，構(gòu)建閥芯運(yùn)動(dòng)力學(xué)模型。2個(gè)模型之間存在力學(xué)關(guān)系，水擊模型計(jì)算得到的水擊壓強(qiáng)可進(jìn)一步確定運(yùn)動(dòng)力學(xué)模型中的氮?dú)鈮毫Α椈闪Φ葦?shù)值，從而解決了泄壓閥的壓力精度設(shè)定問(wèn)題。

2.2 模型構(gòu)建

2.2.1 油氣水三相流耦合水擊模型

在石油工程中，油氣集輸通常采用管道輸送的方式。原油在開采過(guò)程中，輸送介質(zhì)多為油氣水三相流混合流體。油氣水三相流發(fā)生水擊時(shí)，油水兩相和氣相高速運(yùn)動(dòng)，假設(shè)油氣水多相流相間無(wú)質(zhì)量傳遞，無(wú)流型變化，多相流體充滿管道內(nèi)部無(wú)空隙，且按多相混合均質(zhì)流體構(gòu)建模型。在水擊作用下，管道線密度發(fā)生改變，引發(fā)耦合振動(dòng)，考慮振動(dòng)對(duì)水擊壓強(qiáng)的影響，在模型構(gòu)建中引入管道的振動(dòng)速度。發(fā)生水擊時(shí)，忽略流型變化對(duì)水擊壓強(qiáng)的影響，且不作薄壁管假設(shè)，油氣水三相流的耦合水擊模型如下[15]：

管道軸向振動(dòng)微分方程為：

(1)

式中：

(2)

(3)

(4)

(5)

綜合系數(shù)計(jì)算公式為：

I=1/Em+4R(1-μ2)·(R+e)/(2REe+Ee2)

(6)

管壁與流體之間單位長(zhǎng)度的摩擦阻力計(jì)算公式為：

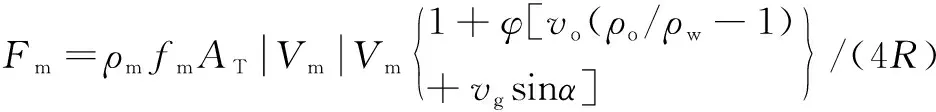
(7)

式中：Vm為多相流體流速，m/s；H為管內(nèi)流體高度，m；U為管道軸向振動(dòng)速度，m/s；σ為管壁軸向應(yīng)力，MPa；E為管材的彈性模量，MPa；μ為泊松比；R為管道內(nèi)半徑，m；e為管壁厚度,m；Ap管壁橫截面積,m2；AT為管道內(nèi)截面積,m2；ρm為管材的密度,kg/m3；g為重力加速度,m/s2；α為管道傾角,(°)；ρm為多相流體的密度,kg/m3；ρo為油相的密度,kg/m3；ρw為水的密度,kg/m3；ρP為管材密度，kg/m3；vg為氣相的體積分?jǐn)?shù)；I為綜合系數(shù)；Em為混合體的體積彈性模量，MPa；x為管道軸向；t為時(shí)間,s；Fm為管壁與流體之間單位長(zhǎng)度的摩擦阻力，N；fm流體與管壁間的摩阻因數(shù)；φ為壓力系數(shù)。

式(1)的特征方程為|B-λA|=0，由該方程可解出4個(gè)不相等的實(shí)根，即考慮耦合效應(yīng)的水擊波速和軸向應(yīng)力波速：

(8)

(9)

(10)

式中：am為不考慮耦合效應(yīng)的水擊壓力波速，m/s；ap為不考慮耦合效應(yīng)的軸向壓力波速，m/s；Cm為考慮耦合效應(yīng)的水擊波速，m/s；Cp為考慮耦合效應(yīng)的軸向應(yīng)力波速，m/s。

由式(8)計(jì)算得到的考慮耦合效應(yīng)的水擊波速，根據(jù)伯努利方程求水擊壓強(qiáng)，計(jì)算如下：

(11)

式中：Pm為考慮耦合效應(yīng)的水擊壓強(qiáng)，MPa；h為流體鉛錘高度，m；c為流體所得的動(dòng)能，J。

2.2.2 閥芯運(yùn)動(dòng)力學(xué)模型

多相流體作用力，氮?dú)鈮毫蛷椈闪Φ南嗷プ饔茫剐箟洪y閥芯可在泄壓閥殼體水平方向上做往復(fù)運(yùn)動(dòng)，根據(jù)動(dòng)力學(xué)理論，對(duì)泄壓閥閥芯運(yùn)動(dòng)狀態(tài)及閥芯受力情況進(jìn)行分析[16]。

氮?dú)馐剿畵粜箟洪y的結(jié)構(gòu)如圖1所示，閥芯受力分析如圖2所示：

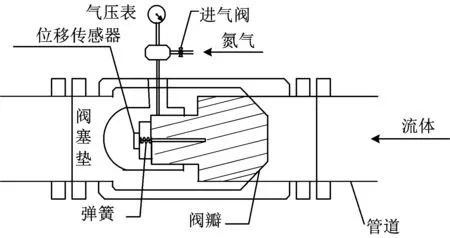
圖1 氮?dú)馐剿畵粜箟洪y結(jié)構(gòu)示意Fig.1 Schematic diagram of the structure of nitrogen-type water pressure relief valve

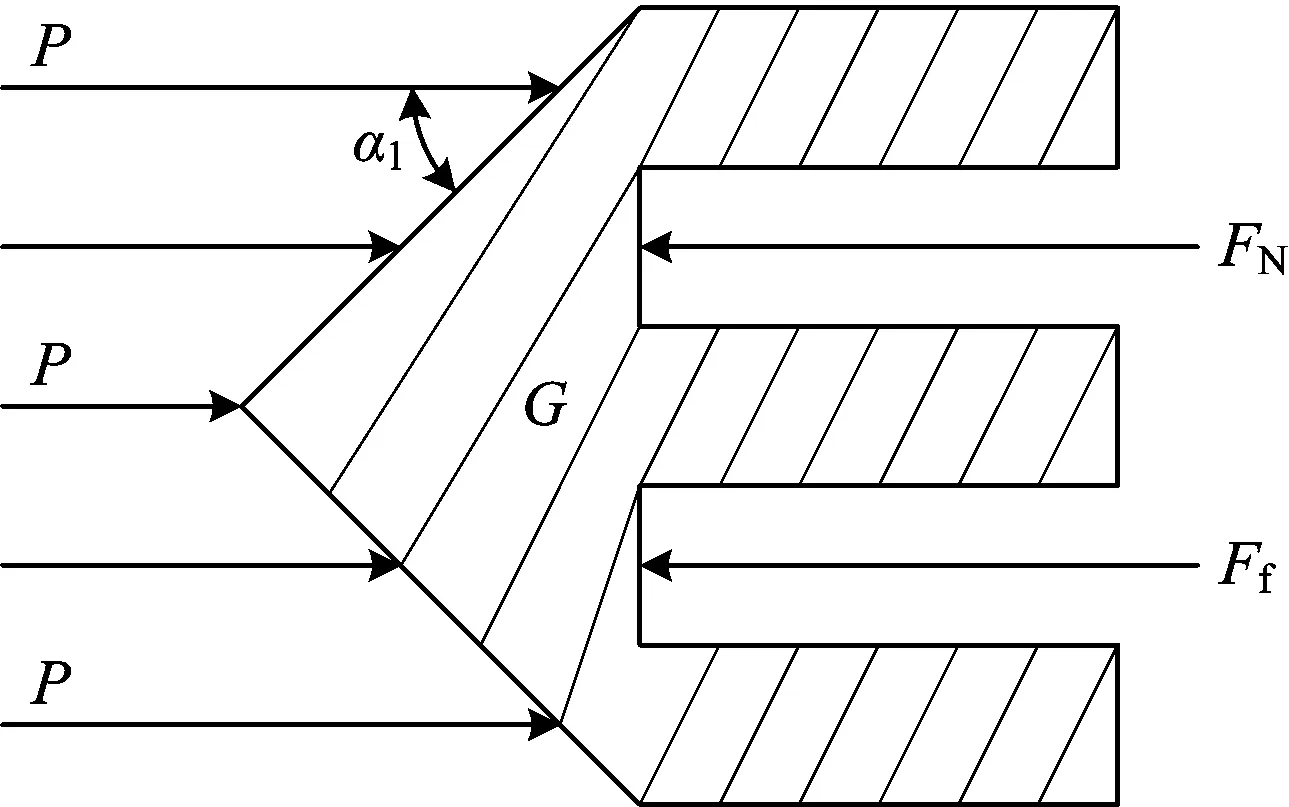
圖2 閥芯受力分析Fig.2 The force analysis figure of valve core

根據(jù)牛頓第二定律，結(jié)合閥芯在水平方向上的運(yùn)動(dòng)狀態(tài)分析，氮?dú)鈮毫τ?jì)算如下：

FN=F-ma-Gμ-Ff

(12)

加速度a的表達(dá)式可寫成如下形式：

(13)

閥芯運(yùn)動(dòng)距離等于彈簧位移量Δx，計(jì)算公式為：

(14)

彈簧作用力計(jì)算公式為：

Ff=KΔx

(15)

其中：m為閥芯質(zhì)量，kg；FN為閥芯腔室內(nèi)氮?dú)鈮毫Γ琋；G為閥芯的重力，N；Ff為彈簧力，N；μ為閥芯與閥壁間的摩擦阻力系數(shù)；a為閥芯運(yùn)動(dòng)方向的加速度，m/s2；vt+Δt為閥芯的在t+Δt 時(shí)刻的運(yùn)動(dòng)速度，m/s；vt為閥芯的在t 時(shí)刻的運(yùn)動(dòng)速度，m/s；Δt為時(shí)間變化量，s；K為彈簧剛度，N/m；Δx為彈簧的位移變化量，m。

3 水擊模型與運(yùn)動(dòng)力學(xué)模型關(guān)系分析

氮?dú)馐剿畵粜箟洪y壓力精度設(shè)定問(wèn)題的影響因素主要是氮?dú)鈮毫蛷椈闪Α闇?zhǔn)確設(shè)定符合管道實(shí)際工況的壓力精度，考慮到水擊壓強(qiáng)、氮?dú)鈮毫εc彈簧力之間存在的力學(xué)關(guān)系，通過(guò)數(shù)學(xué)推導(dǎo)，為泄壓閥的壓力精度設(shè)定問(wèn)題提供理論指導(dǎo)。

管道發(fā)生水擊問(wèn)題形成的瞬時(shí)水擊壓強(qiáng)作用在水擊泄壓閥上，產(chǎn)生對(duì)水擊泄壓閥的水擊作用力，根據(jù)兩者的力學(xué)關(guān)系，構(gòu)建水擊壓強(qiáng)與水擊作用力的數(shù)學(xué)關(guān)系，關(guān)系式如下：

F=Pm·S·sinα1

(16)

式中：F為流體作用力，N；Pm考慮耦合效應(yīng)的水擊壓強(qiáng)，Pa；S為流體在泄壓閥上的作用面積，m2；α1為流體與泄壓閥閥瓣界面的夾角，(°)。

由閥芯運(yùn)動(dòng)力學(xué)模型中的受力分析可知，根據(jù)水擊作用力可以計(jì)算得出氮?dú)鈮毫蛷椈闪ΑＫ畵裟Ｐ湍軌蛲ㄟ^(guò)計(jì)算，得到準(zhǔn)確的水擊壓強(qiáng)等數(shù)據(jù)，從而根據(jù)公式(12)～(16)，計(jì)算得到氮?dú)鈮毫蛷椈闪Φ脑O(shè)定數(shù)值，解決了氮?dú)馐剿畵粜箟洪y的壓力精度設(shè)定問(wèn)題，大大提高了泄壓閥的靈敏度和可靠性。

4 模型驗(yàn)證與結(jié)果分析

4.1 油氣水多相流水擊試驗(yàn)設(shè)備

試驗(yàn)采用的油氣水多相流水擊測(cè)試裝置如圖3、圖4所示。

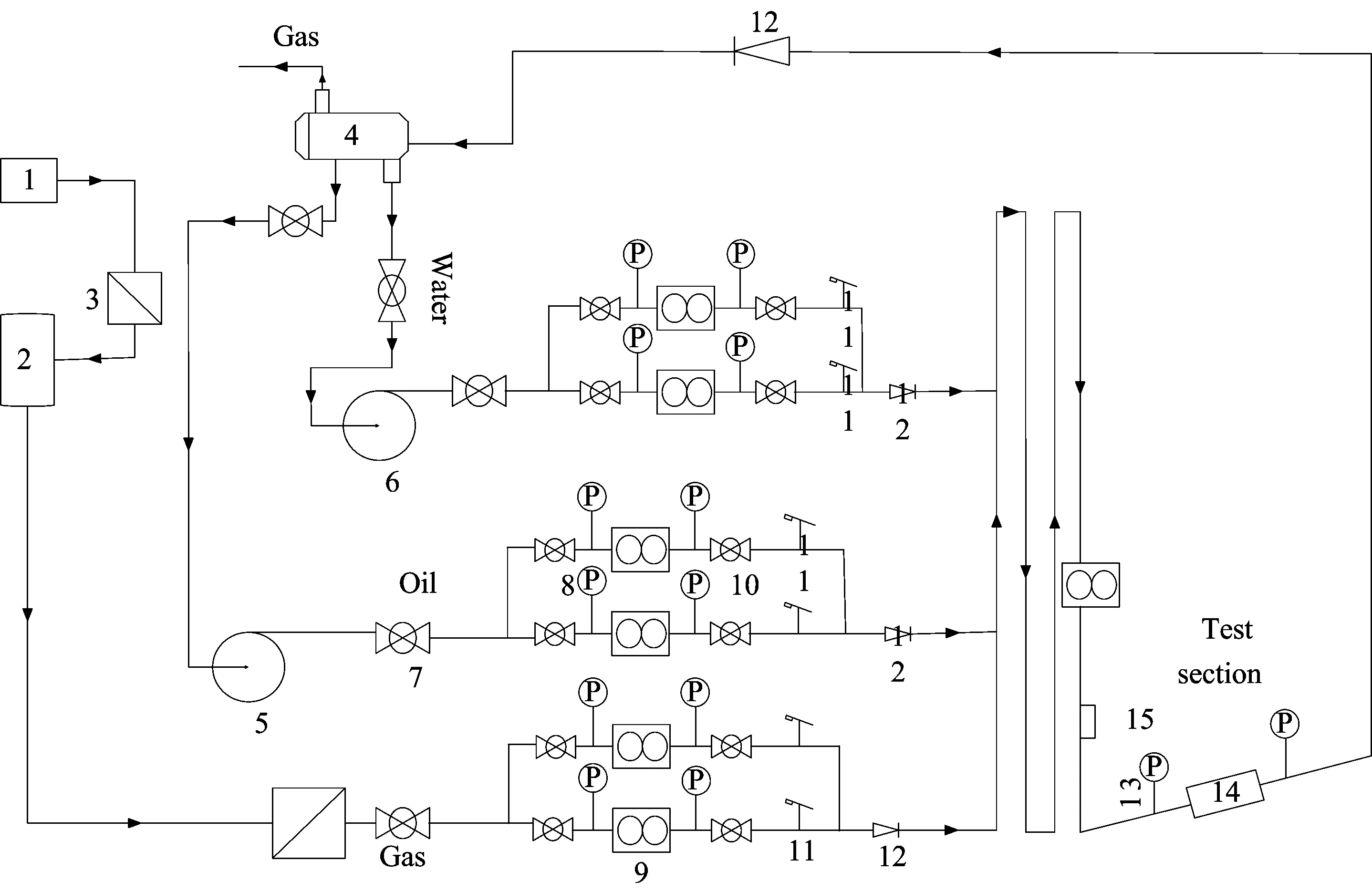
1.空氣壓縮機(jī)；2.穩(wěn)壓管；3.過(guò)濾器；4.三相分離器；5.油泵；6.水泵；7.球閥；8.球閥； 9.流量?jī)x表；10.球閥；11.速開/關(guān)閥；12.止回閥；13.壓力傳感器；14.氮?dú)馐剿畵粜箟洪y；15.振動(dòng)速度傳感器。圖3 油氣水多相流水擊測(cè)試裝置示意Fig.3 Schematic diagram of oil-gas water three-phase flow water hammer test device

圖4 實(shí)驗(yàn)現(xiàn)場(chǎng)照片F(xiàn)ig.4 Photo of the experimental site

4.2 試驗(yàn)方案

油氣水多相流體介質(zhì)分別采用柴油，空氣，自來(lái)水。試驗(yàn)過(guò)程中控制含油率保持0.368不變，按含氣率和含水率之比為1比10的比例進(jìn)行試驗(yàn)。

試驗(yàn)步驟為：1)按圖2測(cè)試裝置示意圖所示安裝布置試驗(yàn)設(shè)備；2)油氣水三相流分別采用油泵、空氣壓縮機(jī)、水泵進(jìn)行泵送；3)采用開閉速(開)關(guān)閥來(lái)改變管道內(nèi)流體的運(yùn)動(dòng)狀態(tài)，從而模擬水擊問(wèn)題；4)根據(jù)試驗(yàn)裝置中的傳感器獲得水擊壓強(qiáng)、管道軸向振動(dòng)速度、閥芯位移量等數(shù)據(jù)；5)根據(jù)試驗(yàn)裝置中的氣壓表、流量表獲得氮?dú)鈮毫Α⒘髁康葦?shù)據(jù)；6)根據(jù)獲得的流量數(shù)值，計(jì)算單位時(shí)間內(nèi)的流量變化情況，從而得到水擊波速。

4.3 實(shí)證與結(jié)果分析

根據(jù)式(1)-(16)進(jìn)行有關(guān)的數(shù)值計(jì)算，計(jì)算結(jié)果與試驗(yàn)結(jié)果對(duì)比分析如圖5、圖6和圖7所示。

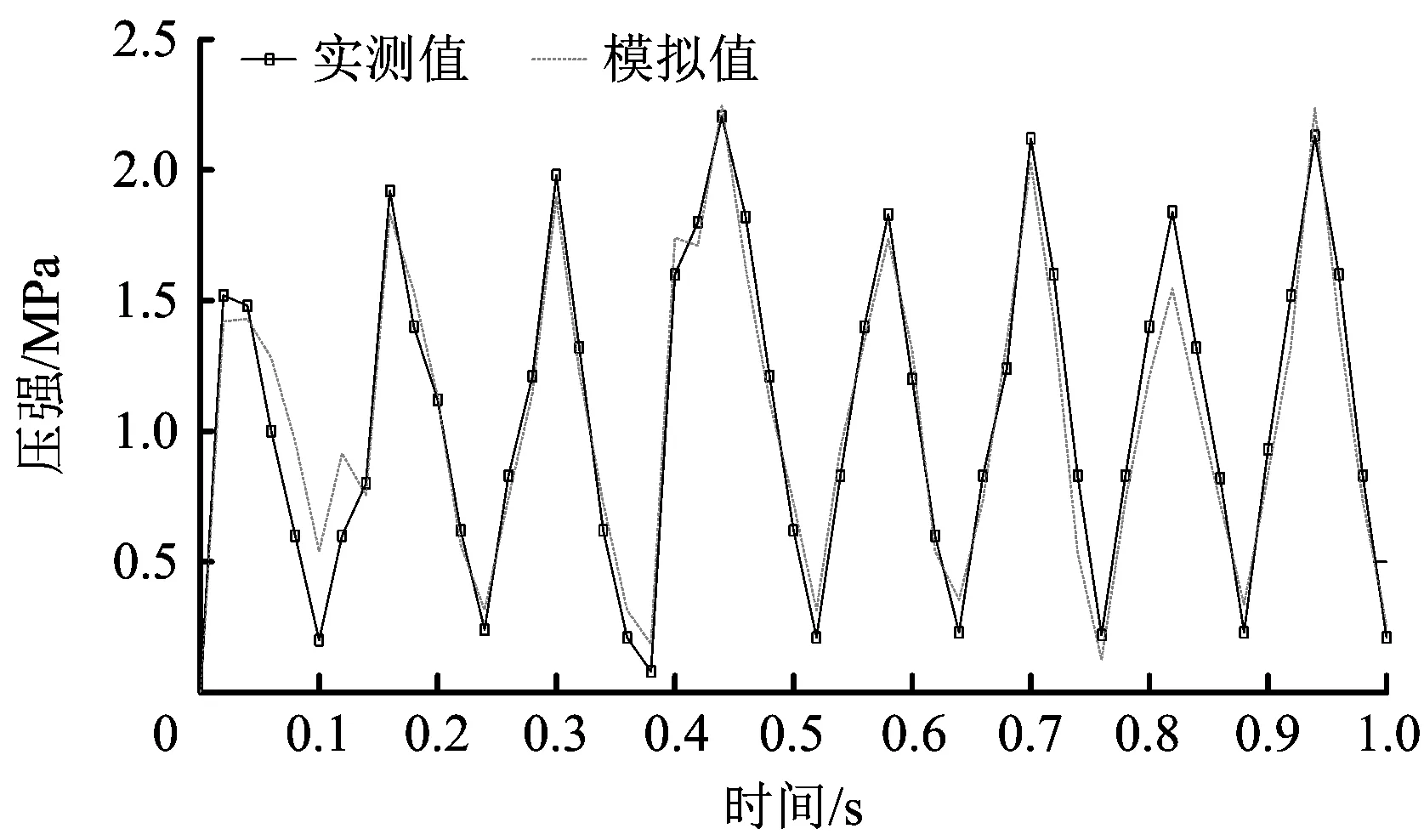
圖5 泄壓閥前端壓強(qiáng)變化情況Fig.5 Pressure change of the front end of the relief valve

圖5為水擊壓強(qiáng)模擬計(jì)算值與實(shí)測(cè)值在圖像上的分布情況，受管道耦合振動(dòng)的影響，泄壓閥前端壓強(qiáng)呈現(xiàn)周期性波動(dòng)，水擊壓強(qiáng)的計(jì)算值與實(shí)測(cè)值的分布曲線基本重合。經(jīng)計(jì)算，水擊壓強(qiáng)計(jì)算值與實(shí)測(cè)值的平均相對(duì)誤差為6.12%。從數(shù)據(jù)反應(yīng)情況看，在泄壓閥前端的壓強(qiáng)由于受到泄壓閥的影響，在壓強(qiáng)達(dá)到1.5 MPa時(shí)，壓強(qiáng)迅速降低。泄壓閥通過(guò)啟閉閥瓣等動(dòng)作，將由水擊引起的管道內(nèi)急劇增大的壓強(qiáng)維持在一個(gè)較安全的范圍內(nèi)，保障油氣管道系統(tǒng)安全運(yùn)行。

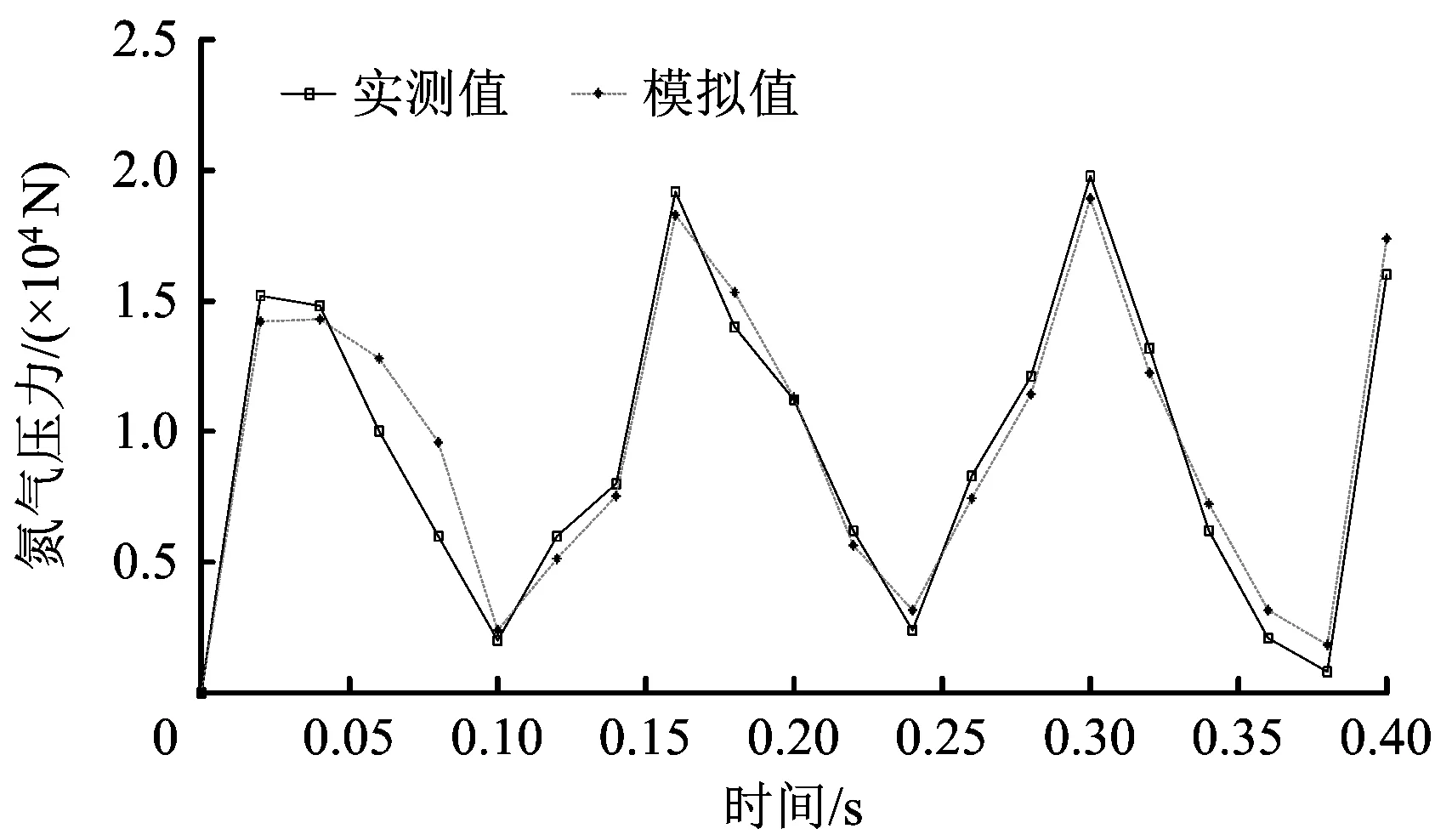
圖6 氮?dú)鈮毫?shí)測(cè)值與模擬值對(duì)比Fig.6 Comparison between measured and simulated values of nitrogen pressure

圖7 彈簧力實(shí)測(cè)值與模擬值對(duì)比Fig.7 Comparison between measured and simulated values of spring force

圖6和圖7分別為氮?dú)鈮毫δM值與實(shí)測(cè)值、彈簧力模擬值與實(shí)測(cè)值在圖像上的分布情況，由于泄壓閥受水擊作用力作用后，泄壓閥的氮?dú)鈮毫蛷椈闪Σ虐l(fā)生周期性變化，變化周期比泄壓閥前端的水擊壓強(qiáng)的變化周期稍長(zhǎng)。氮?dú)鈮毫?shí)測(cè)值與模擬值的分布曲線基本重合，彈簧力實(shí)測(cè)值與模擬值的分布曲線基本重合。經(jīng)計(jì)算比較，氮?dú)鈮毫Φ哪M值與實(shí)測(cè)值的平均相對(duì)誤差為4.31%，彈簧力的模擬值與實(shí)測(cè)值的平均相對(duì)誤差為3.22%，計(jì)算精度較高，通過(guò)水擊壓強(qiáng)可以進(jìn)一步確定氮?dú)鈮毫εc彈簧力。

5 結(jié)論

1)考慮管道耦合振動(dòng)對(duì)水擊壓強(qiáng)等數(shù)值的影響，能準(zhǔn)確地模擬在流固耦合作用下水擊壓強(qiáng)的變化過(guò)程。根據(jù)油氣水三相流耦合水擊模型計(jì)算得到的水擊壓強(qiáng)與實(shí)測(cè)值基本吻合，計(jì)算平均相對(duì)誤差為6.12%，計(jì)算精度高。

2)結(jié)合泄壓閥的受力情況，得到了氮?dú)鈮毫Α椈闪εc水擊壓強(qiáng)之間的力學(xué)關(guān)系。發(fā)生水擊時(shí)，氮?dú)鈮毫Α椈闪εc水擊壓強(qiáng)大小呈周期性變化，單個(gè)周期內(nèi)先增大后減小。

3)利用水擊壓強(qiáng)、氮?dú)鈮毫蛷椈闪χg的力學(xué)關(guān)系，將油氣水三相流耦合水擊模型與閥芯運(yùn)動(dòng)力學(xué)模型結(jié)合起來(lái)，得到水擊壓強(qiáng)后可以進(jìn)一步確定氮?dú)鈮毫蛷椈闪Α５獨(dú)鈮毫δM值與實(shí)測(cè)值的平均相對(duì)誤差為4.31%，彈簧力模擬值與實(shí)測(cè)值的平均相對(duì)誤差為3.22%。氮?dú)鈮毫蛷椈闪υO(shè)定數(shù)值的確定，解決了氮?dú)馐剿畵粜箟洪y壓力精度的設(shè)定問(wèn)題，這對(duì)保障油氣管道系統(tǒng)的安全運(yùn)行具有重要的指導(dǎo)意義。