基于人工魚群改進粗糙集的裝備器材物流效益評估

朱 臣，朱 倩，陳 晨 ZHU Chen,ZHU Qian,CHEN Chen

（1.空軍勤務學院，江蘇 徐州 221000；2.陸軍裝甲兵學院，北京 100000）

(1.Air Force Logistics University,Xuzhou 221000,China;2.Army Armor Academy,Beijing 100000,China)

0 引言

裝備器材物流是裝備器材有采購、運輸、儲存、包裝、裝載搬運、維護保養、配送等環節，最終抵達保障單位，實現裝備器材空間轉移的全過程[1]。裝備器材物流是承擔軍用裝備供應保障任務的一種特殊物流，其追求完成保障任務既要講求經濟效益，更要追求軍事效益，即追求軍事和經濟效益的雙贏[2]。因此，選擇合適的裝備器材物流方案至關重要，對物流方案的物流效益科學評估十分必要，可以為裝備器材保障部門決策者提供有力參考。

粗糙集理論作為一種處理不精確、不一致、不完整等信息的有效工具，可以從現有數據中發現隱含的知識，揭示潛在的規律，是一種天然的數據挖掘或是知識發掘的方法[3]。人工魚群算法是一種智能算法，模仿魚群覓食、聚群及追尾行為，從而實現尋優。該算法具有較快的收斂速度，可以用它快速得到最優解[4]。在用粗糙集解決實際問題的過程中，往往會遇到屬性值是連續的或者是一個真實的數據，這時需要將這些數據進行離散化處理。通過人工魚群算法對粗糙集實現離散化，既可以減少屬性離散化后的空間維數又能降低屬性值被離散化后丟失的信息。本文通過人工魚群算法改進粗糙集理論，建立有效的定量評估方法，提高裝備器材物流方案的科學性，為裝備器材保障實際工作提供理論指導。裝備器材物流效益評估思路如圖1所示。

1 理論基礎

1.1 信息熵概述

信息是事物運動狀態或存在的“不確定性”描述。通信的過程就是一種消除不確定性的過程；不確定性消除的越多，獲得的信息量就越多[5]。由此，信息熵是“不確定性”對信息的度量。

定義1 若事件x發生的概率是p（x），則x帶來的信息量稱為x的自信息，記為I（x），且I（x）=-ln p（x）。進一步地，一個離散信息源平均自信息（自信息的期望）就是信源X的熵H（）X ，即：

圖1 裝備器材物流效益評估思路

1.2 粗糙集概述

在粗糙集理論中，將信息表知識表達系統定義為S=＜U,R,V,f＞，其中：U為論域；R=C∪D為屬性集合（C為條件屬性集，D為決策屬性集）；為屬性值的集合（Vr為屬性r的值域）；f：U×R→V為一個映射函數，通過f可以確定U中每個對象的屬性值[6]。

定義2 若P?R,P≠?，則P中的全部等價關系的交集稱為P上的不可分辨關系（Indiscernility Relation），記為：

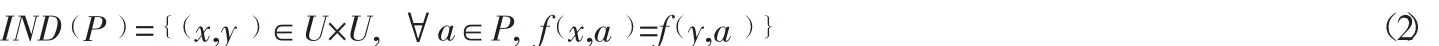
不可分辨關系也稱等價關系，它把劃分為有限個集合，稱為等價類。在每個等價集合中，對象是不可分辨關系。對于?x∈U，它的P等價類定義：

在一個信息系統中，所有的信息并不是同等重要的，有些甚至是冗余的，要想得到更為簡捷的決策規則，就必須對粗糙集中的屬性進行約簡。

1.3 人工魚群算法簡介

人工魚群算法是由李曉磊博士提出來的，是一種自下而上的新型尋優算法，它具有魯棒性強、全局收斂性好、對初值的敏感性小等優勢，該算法通過模擬魚的覓食行為、聚群行為、追尾行為和隨機行為自動進行全局尋優[7-8]。

覓食行為：設人工魚i當前狀態為Xi，在其感知范圍內隨機選擇一個狀態Xj：

其中：Rand（）為介于0到1之間的隨機數，若該狀態食物濃度大于當前狀態，則向該方向前進一步：

反復嘗試n次后，若仍不滿足條件，則隨機移動一步：

聚群行為：設人工魚當前狀態為Xi，探索當前領域內 （dij＜ Visua l）的伙伴數目nf及中心位置Xc。若Yc/nf＞δYi，表明中心位置食物濃度較高且不擁擠，則朝中心位置前進一步：

否則執行覓食行為。

追尾行為：設人工魚i當前狀態為Xi，探索當前領域內 （dij＜ Visua l）的伙伴中Yj為最大值的伙伴Xj。若Yc/nf＞δYi，表明中心位置食物濃度較高且不擁擠，則朝Xj前進一步：

隨機行為：人工魚在視野中隨機選擇一個狀態，然后向該方向移動。

在人工魚群算法中，覓食行為奠定了算法收斂的基礎，聚群行為增強了算法收斂的穩定性，追尾行為增強了算法收斂的快速性和全局性。

2 評估步驟

2.1 構建評估決策系統

做好裝備器材保障工作，才能保證軍隊戰斗力的生成。裝備器材保障工作的特殊性，就注定在評估裝備器材物流效益時，要把“軍事效益”放在首位。而且，軍用裝備器材價格十分昂貴，其運輸成本與本身價格相比相形見絀，要把“經濟效益”放在次位。于是，在評估裝備器材物流效益時，著重考慮其“軍事效益”。通過查閱相關文獻，選取以下5個指標：單位時間內完成裝備器材周轉量（噸·公里/月），裝備器材交貨準確率（%），裝備器材訂單完成率（%），裝備器材發貨破損率（%），裝備器材發貨響應時間（天）。

（1）單位時間內完成裝備器材周轉量是指通過各種運輸工具，每月實際運輸的裝備器材重量乘以運送距離的累計數。

裝備器材周轉量=實際運輸裝備器材噸數×平均運輸距離

（2）裝備器材交貨準確率是指在已交裝備器材總數量占應交裝備器材總數量的百分比。

裝備器材交貨準確率=已交裝備器材總數量/應交裝備器材總數量×100%

（3）裝備器材訂單完成率是指已完成裝備器材訂單總數量占應完成裝備器材訂單總數量的百分比。

裝備器材訂單完成率=已完成裝備器材訂單總數量/應完成裝備器材訂單總數量×100%

（4）裝備器材發貨破損率是指在運輸過程中破損的裝備器材總數量占已發出裝備器材總數量的百分比。

裝備器材發貨破損率=運輸過程中破損的裝備器材總數量/已發出裝備器材總數量×100%

（5）裝備器材發貨響應時間是指物流單位接到裝備器材訂單到將裝備器材發出的時間間隔。構建初始信息表，并形成條件屬性：

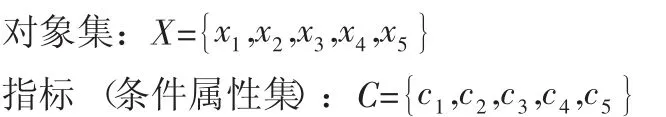
式中：x1,x2,x3,x4,x5為5個物流方案，c1為單位時間內完成裝備器材周轉量（噸·公里/月），c2為裝備器材交貨準確率（%），c3為裝備器材訂單完成率（%），c4為裝備器材發貨破損率（%），c5為裝備器材發貨響應時間（天）。

具體評估決策系統初始信息表如表1所示。

表1 評估決策系統初始信息表

2.2 利用信息熵和人工魚群改進粗糙集算法評估

2.2.1 基于信息熵的權重確定。指標權重作為各評估指標對于評估方案影響程度的反映。基于信息熵確定權重的計算步驟如下：

（1）通過對象集U上m個決策對象對n個決策屬性評估，可以得到特征值矩陣，特征值矩陣λ表示：

（2）對矩陣R=rij（）m×n進行列歸一化，得到，其中：

（3） 計算屬性aj輸出的信息熵：

（4）計算屬性權重向量：

采用上述步驟即可以計算出多屬性決策表屬性的權重，其中：ωj為aj的權重。

2.2.2 基于人工魚群的連續屬性離散化步驟。基于人工魚群的連續屬性離散化算法如下：

Step1：對人工魚群算法進行初始化設置，包括人工魚個數Fishnum、初始位置、移動步長Step、感知距離Visual、試探次數Try_number和擁擠度因子Delta。

Step2：根據人工魚的當前狀態對條件屬性進行離散化，并將支持度設置為人工魚群算法的尋優函數[9]：

Step3：人工魚執行各種行為，并進行多次迭代，比較KC（D）的值，記錄全局最優的人工魚狀態。

Step4：當KC（D）達到最大穩定值時，人工魚的當前狀態即為連續條件屬性的分割點，若KC（D ）不符合要求則轉到Step2。

2.2.3 基于差別矩陣的屬性約簡。利用差別矩陣對屬性進行約簡是目前常用的一種方法。在信息系統S=（U, A ,…,f）中，U=n。屬性集P?A的差別矩陣M（P）是一個n×n矩陣，其任一個元素為：

如果屬性集A=C∪D，其中C為條件屬性集，D為決策屬性集，則可定義（C,D）差別矩陣，記為M（C,D）[10]。那么：

當［x］C≠ ［y］C和［x］D≠ ［y］D時：

當［x］C=［y］C和［x］D=［y］D時：

2.2.4 計算在屬性指標下相對決策屬性的權重表。通過計算方案及對于每個屬性的分類。定義：

稱為決策屬性的第s個等價類與每個條件屬性的等價類間的等價近似度，取MAX，記為對象在決策屬性中的局部權重。利用上述公式，得到各個屬性在屬性指標下相對于決策屬性的權重表。最后得到量化物流的指標為：

將衡量指標進行排序，即可得到裝備器材物流效益評估排序。

3 實例驗證

引用上述評估方法，對5個物流方案進行評估決策。

5個裝備器材物流評估指標信息如表2所示。

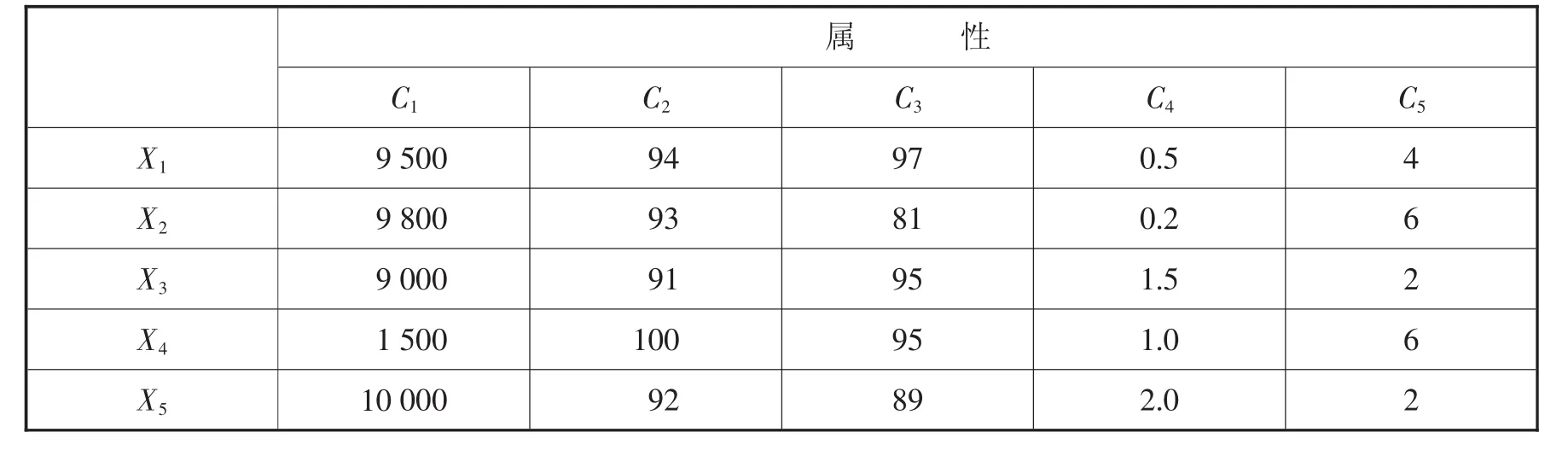
表2 裝備器材物流定量指標信息

首先對裝備器材物流評估指標信息進行處理。利用式（9）求出表2的特征矩陣，并結合式（10）對得到的特征值矩陣進行歸一化處理，得到歸一化決策矩陣，如表3所示。

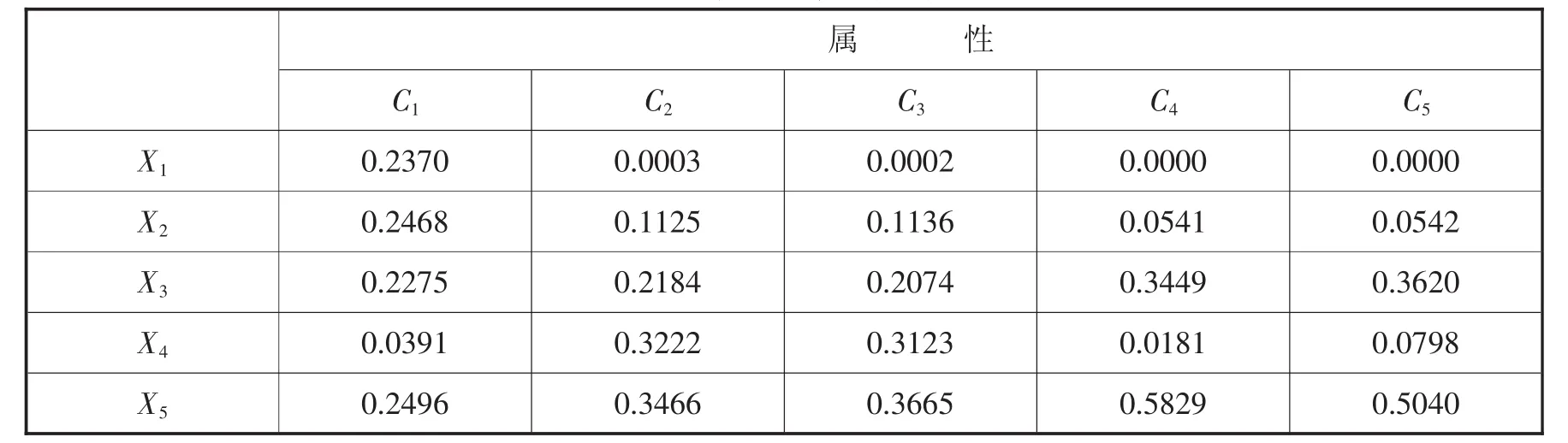
表3 歸一化決策矩陣

計算得到條件屬性C1、C2、C3、C4、C5的信息熵，如表4所示。

表4 條件屬性的信息熵

計算條件屬性C1、C2、C3、C4、C5的屬性權重如表5所示。

可以從表5中發現，單位時間內完成裝備器材周轉量C1的權重最大。對物流效益評估而言，單位時間內完成裝備器材周轉量能間接反映該裝備器材物流方案的運行效率，良好的運行效率保證著良好軍事效益。結合上述模型，可以將單位時間內完成裝備器材周轉量看成粗糙集理論中的決策屬性D，用于評估物流方案的綜合效益。

表5 條件屬性的權重

采用人工魚群算法對表2連續變C1、C2、C3、C4、C5進行離散化，其中人工魚群個數Fishnum=100，初始位置設置在最大值與最小值之間，移動步長Step=0.05，感知距離Visual=0.05，試探次數Try_number=100，擁擠度因子Delta=0.638。通過MATLAB編程運算尋得最優極值點及離散化后的指標信息。

圖2為人工魚群算法的尋優曲線，從圖中可以看出該算法收斂速度較快，并且隨著迭代次數的不斷增加，優化結果可逼近到最優值極點。

表6為各參數離散化后，構建的完備信息決策表。

得到差別矩陣，如表7所示。

圖2 尋優曲線

表6 離散化后的信息決策表

表7 差別矩陣

進而可得，C2、C4為核心屬性，C3、C5為相對必要屬性，沒有不必要屬性，從而不需要屬性約簡。

在決策系統中，每個屬性的等價關系得到的分類如下：

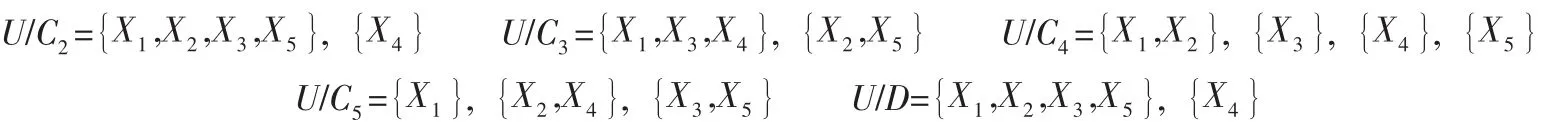
基于粗糙集多屬性決策的排序法，得到5個裝備器材物流方案在每個指標相對于決策屬性的權重如表8所示。

運用式（18）得到5個裝備器材物流方案的度量值T，如表9所示。

根據各度量值T，得到裝備器材物流方案的排序為：X5＞X1=X3＞X2＞X4。

顯而易見，X5的評估結果相對其他最好，因此在選擇裝備器材物流方案時，應給予優先考慮。

4 結論

本文結合裝備器材保障的特點，把“軍事效益”放在首位，建立了裝備器材物流評估模型。該模型在沒有決策信息條件下，采用信息熵的方法求得最大權重屬性代替決策屬性，拓展了粗糙集的適用范圍，并利用人工魚群對粗糙集連續屬性離散化，減少人為因素對評估結果的影響，增強評估的科學性、有效性。最后結合實例，進一步表明評估模型的適用性，能為今后裝備器材物流方案選取上提供理論支撐。

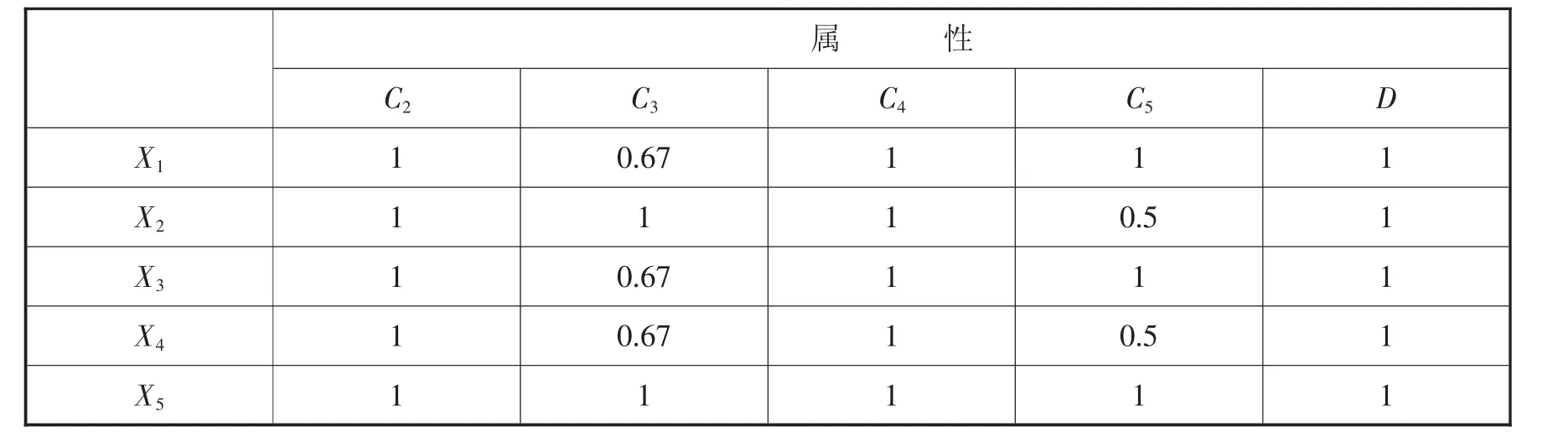
表8 指標相對于決策屬性的權重

表9 5個裝備器材物流的度量值T