考慮庫存調撥下的雙渠道多級分銷網絡ATC優化配置方法

王 帥，屈 挺，張 婷，李從東，黃國全,4

WANG Shuai1,QU Ting2,3,ZHANG Ting1,LI Congdong2,HUANG Guoquan2,4

（1.廣東工業大學 廣東省計算機集成制造重點實驗室，廣東 廣州 510006；2.暨南大學 物聯網與物流工程研究院，廣東 珠海519070；3.暨南大學 電氣信息學院，廣東 珠海 519070；4.香港大學，香港）

(1.Guangdong CIMS Provincial Key Lab,Guangdong University of Technology,Guangzhou 510006,China;2.Institute of Physical Internet,Jinan University,Zhuhai 519070,China;3.School of Electrical and Information Engineering,Jinan University,Zhuhai 519070,China;4.The University of Hong Kong,Hong Kong,China)

隨著電子商務和物流行業的迅猛發展，企業為了擴大市場，越來越多的企業開始將網絡直銷渠道融入其原有的分銷體系實施雙渠道銷售策略，形成線上線下銷售互補的新型經營模式[1]。雖然，雙渠道銷售為企業的發展帶來了新的契機。但是，作為一種新興銷售模式，客戶線上訂單的產生規律難以預測，因而造成線上庫存量無法準確設置；同時，由于新產品頻繁推出，在售產品的線下銷售量也常常受到動態沖擊而呈現大幅不確定性，因而線下庫存也常常出現過剩或者不足的情況。因此，需要把線上線下庫存打通，通過需求波動的對沖減少總庫存量。而庫存調撥是一種庫存共享方式，它可以協調參與者之間的需求與供給，實現風險分擔、物資再分配、減少缺貨損失，進而使得兩種銷售渠道的需求都能夠得到最大程度的滿足[2]。隨著供應鏈管理思想的逐漸發展與理論的成功，雙渠道多級庫存控制問題也逐漸成為企業和學術界普遍關注的焦點。有效地管理和控制多級庫存系統，是提高顧客服務水平和供應鏈運作效率的關鍵因素之一。因此，考慮庫存調撥機制下的雙渠道多級分銷庫存網絡優化配置是一個值得研究的問題，具有豐富的指導意義。

雙渠道供應鏈的研究目前主要集中在協調契約、利益分配、定價策略等方面，而對于庫存管理方面的研究則較少。文獻[3-5]研究了制造商在現行制定批發價與線上零售價時，線下零售商參考制造商的價格策略通過博弈來制定自己的價格策略。調撥機制下雙渠道多級分銷的研究主要集中在兩級雙渠道供應鏈，而且多為單周期。文獻[6]研究的是單周期的庫存調撥問題，是在缺貨發生后而做的一種緊急應對補救措施。目前對于研究雙渠道多周期且多級（三級及以上）分銷網絡幾乎很少涉及。即在雙渠道多級分銷網絡中，為了降低未來缺貨的發生，很少在前期庫存配置分析的基礎上同時將缺貨調撥考慮在內。所以本文將研究庫存調撥下的多周期庫存配置問題，在保證庫存成本最低的情況下，盡可能地降低未來缺貨發生的可能性。在方法上，求解多采用馬爾科夫鏈[7-8]、博弈論[2,9-11]等。隨著雙渠道多級分銷型供應鏈的日益發展，更迫切地需要一種支持可擴展型的協調優化方法，將分散的具有自主決策的各級分銷商納入平臺運作，動態而迅速地配置形成滿足特定需求的雙渠道多級分銷型供應鏈系統。

目標級聯分析法（Analytical Target Cascading，ATC）是一種基于分解策略的復雜大系統優化方法[12]。其基本理念是將對象系統按可行決策區間分解為由獨立決策單元組成的層級式決策體系；將優化目標從最高級進行層疊式下放，并將相關決策單元進行逐層優化求解；可行目標逐級下放直至底層優化結束，而非可行目標將造成回滾修正并觸發下一輪層疊優化，而整個過程由ATC協調規則進行約束。Huang和Qu[12-13]等使用了拓展的ATC對供應鏈優化配置問題進行多學科分布式優化求解，以在提升整體優化效率的同時保留供應商的自主決策權。ATC對于解決可分解為層級式體系結構的復雜大系統優化具有可并行優化、層級數不受限制和經過嚴格的收斂證明等優點。

為保持研究結果的通用性，從而避免建模和計算的復雜度，本文面向具有雙渠道多級分銷庫存網絡的一類企業為研究對象。針對中心倉、分銷商、零售商的線上線下顧客隨機需求，為了降低未來缺貨發生的可能性，研究考慮同層級庫存調撥機制下的雙渠道多級分銷庫存網絡優化配置問題，進而實現低成本、快速響應、提高顧客服務水平的目標。本文主要研究的問題包括：（1）同層級庫存調撥機制；（2）雙渠道多級分銷網絡的ATC建模步驟和求解方法；（3）對比研究ATC與傳統計算方法的計算效果和效率。

1 問題描述

1.1 雙渠道多級分銷庫存結構的運作模式

本文針對具有雙渠道多級分銷庫存結構的一類企業開展研究。雙渠道多級分銷網絡結構如圖1所示：

該類企業通常包含如下4類：

（1）集團層：為系統最高管理決策層，除了運營電商平臺外不直接參與倉儲銷售。線上客戶通過電商平臺下訂單，然后集團根據顧客線上需求來源，如地理位置等，將訂單分配到距離最近的分銷節點，進而使該節點滿足其區域內線上客戶的需求。故承擔著接單和分單的職能。

（2）中心倉層：經常設立在交通發達、人口消費密集的大中型城市。從供應商的所有進貨都先存儲在幾個中心倉。為了滿足雙渠道的訂單需求，會將庫存按比例劃分為線上與線下庫存。線下庫存主要滿足各分銷商的訂購需求。線上庫存會根據集團分配的訂單任務，進行線上訂單的配送。不參與面向終端客戶的線下零售。故承擔著線下分銷和線上配送的職能。

（3）分銷商層：這類分銷商不僅具有倉儲職能，還有銷售職能。同樣會將庫存按比例劃分為線上與線下庫存。線下庫存滿足其管轄的下級零售商訂購需求和面向終端客戶的線下零售。線上庫存會根據集團分配的訂單任務，滿足此區域線上客戶的需求。故承擔著線下分銷、線下零售和線上配送的職能。

（4）零售商層：銷售網絡中的最底層。線下庫存直接面向終端客戶進行線下零售。線上庫存會根據集團分配的訂單任務，進行線上配送。故承擔著線下零售和線上配送的職能。

1.2 同層級庫存調撥機制

在圖1的運作模式下，由于顧客需求的隨機性和區域需求的不均衡性，未來經常會發生渠道缺貨的情況。盡早制定調撥方案可幫助各商家規避缺貨風險，從而使得整個供應鏈系統的庫存水平更加穩定。同層級庫存調撥機制如下：當一個節點內線下有需求時，首先由該節點下的線下庫存進行滿足；如果該節點線下庫存不能滿足客戶需求時，通過該節點下的線上剩余庫存轉運來滿足；如果該節點線上線下庫存都無法滿足時，則通過同一供應商管轄下的其它同層級節點的剩余庫存進行轉運來滿足；如果同層級節點庫存也不能滿足該客戶需求時，則等待下一周期進行補貨。

1.3 難點分析

（1）可擴展型結構。其層級式結構是可擴展型的，即不同地區擁有不同的子庫存系統，這不僅體現在子系統中節點的數量上，而且體現在節點間的非確定性層級上。

（2）不確定分支數量。本文研究貼近現實的不確定下屬分支和節點的情況，面對不同地區、不同渠道來源的訂單，這會造成數學模型中分支數量的不確定。

（3）復雜函數關聯。由于層級式組織結構的特點及其下轄各節點間形成的特定關系，會產生如多節點追求同一目標等需求。導致本系統整體優化配置無法采用基于變量關聯的半分離式模型的傳統MDO方法。

上述特點使得采用傳統一體式優化方法求解此類問題變得極為困難。而ATC方法適用于解決復雜層級式結構及支持函數、變量多重耦合的特點，為解決上述具有多層級、深層次耦合關系的多子系統協同設計提供了可能的求解手段。

1.4 問題假設

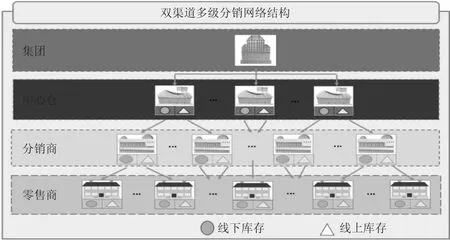
圖1 雙渠道多級分銷網絡結構

（1）各節點顧客需求服從獨立的泊松分布，即消費者泊松到達。

（2）將分銷商線下批發與線下零售兩類需求統一歸為線下需求，減少計算的復雜度。

（3）線上線下顧客需求具有同等的優先級，保證兩類顧客享受同等的服務。

（4）系統采用Q,（）r連續盤點補貨策略。

1.5 符號說明

主要參數的符號和相關定義如表1所示。

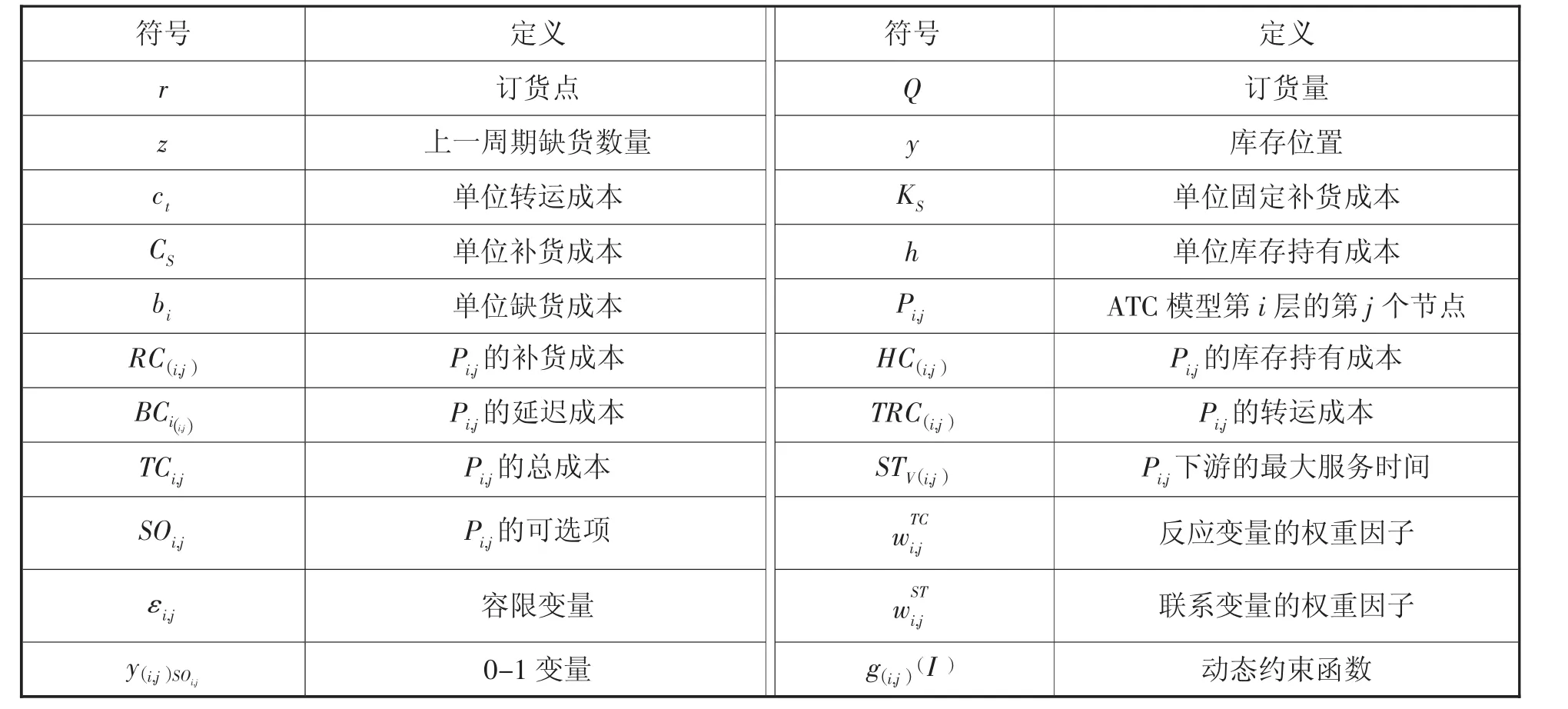
表1 參數符號與定義

2 雙渠道多級分銷供應鏈ATC優化配置模型

2.1 模型描述

為了降低計算的復雜度和難度，允許每個節點下邊有兩個子節點，如圖2所示的配置模型。針對中心倉、分銷商、零售商的多類顧客（線上、線下）隨機需求，研究雙渠道多級分銷網絡下的多周期庫存配置問題。并在多周期庫存配置過程當中，某一渠道發生缺貨時，研究通過同層級庫存調撥使得系統各分銷節點庫存水平的平衡，以此來達到企業整體庫存成本和服務時間為最優的決策問題。

圖2 雙渠道多級分銷網絡結構配置模型

2.2 系統ATC模型

應用ATC方法求解復雜系統的步驟[12-13]：第一步，建立正確的且具有分層結構的ATC目標系統模型；第二步，標明各層系統間的關鍵連接量，包括響應量和連接變量，響應量是父子系統元素之間共享量，連接變量是子系統元素共享量；第三步，建立各層系統局部目標函數模型；第四步，根據文獻選擇ATC求解策略；第五步，選擇求解協調方法（如權重更新法、罰函數法等），求解優化各層系統局部目標。基于上述步驟，本文將對中心倉、分銷商、零售商各層建模。

2.2.1 中心倉層的ATC數學建模

中心倉層以節點1.（）1為例進行建模，其它中心倉層節點建模類似。

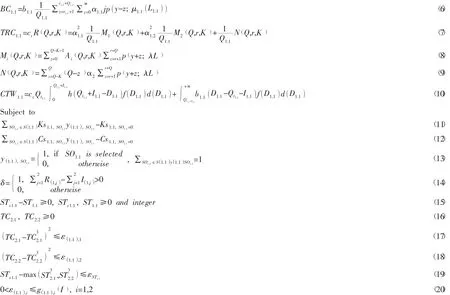
目標函數（1）：

tTC是tST中心倉（階段1.1） 總成本（TC）和服務時間的兩個需求目標。為了使得總成本和顧客服務時間最優，tTC和tST經常設為0。TC1.1和ST1.1，階段1.1的總成本和服務時間，被作為保持下游聯系的反應變量。作為權重因子，指的是客戶對目標的偏好程度。容限變量 ε（1.1）,1,ε（1.1）,2,εST1.1保持下游的聯系。

分析模型 （2） ～ （10）：

AM1.1（TC）和AM1.1（ST）是TC1.1和ST1.1的分析模型。階段1.1的總成本TC1.1是當前階段 （δ（RC1.1+HC1.1+BC1.1+TRC1.1）+（1-δ）CTW1.1）與下游階段 （TC2.1+TC2.2）的總和。其中，當δ=1時，1.1內部線上線下產生的庫存成本，包括節點內某一渠道發生而產生的轉運成本。當δ=0時，節點內的調撥量已經無法滿足需求，此時通過同層級之間的調撥滿足客戶的需求。由于AM1.1（ST）比較簡單，所以輸入和輸出都是ST1.1，這是因為ST1.1即是反應變量又是聯系變量。式（4）為補貨成本；式（5）庫存持有成本等于單位庫存持有成本h與期望現貨OH（Q,r,k）的乘積；式（6）缺貨成本等于單位缺貨成本bi與期望缺貨數量Bi（Q,r）的表達式；式（7） 轉運成本等于單位轉運成本Ct與節點內部期望轉運數量R（Q,r,k）的表達式；p（y-z;λL）和p（y+z;λL）是指數分布；αi是單個供應商需求與總需求的比值。式（10）是節點外調撥而產生相應的庫存費用。

限制條件 （11） ～ （20）：

式（11） ～（13） 指的是單位固定補貨成本（Ks）與單位運輸成本（Cs）在階段1.1中只有一個選項被選擇。式（14） 代表是節點內調撥還是節點外調撥。式（15）指的是來自下游的服務時間作為實際輸入服務時間STV1.1。式（16）指的是TC的所有低層級反應都為正值。式（17）～（20）代表的是容限約束，保證所有的低層級關鍵聯系都在容限變量范圍內。為了保持階段之間的一致性，每一個容限變量也應該限制在動態約束函數g0,i（I）中。

2.2.2 分銷商層的ATC數學建模

2013年第23號強臺風“菲特”人員傷亡大幅度減少，為同級別臺風傷亡人數最少。究其原因，主要是對臨山、臨海、臨江等一切危險地段的人員，都科學、梯次、及時、全面地予以轉移，全市人員轉移規模近35萬人。實踐證明，面對強臺風災害，只有堅持以人為本，果斷采取避險措施，將危險地段的人員轉移出去，才能有效地減少人員傷亡。

分銷商層以節點2.（）1為例進行建模，其它分銷商層節點建模類似。

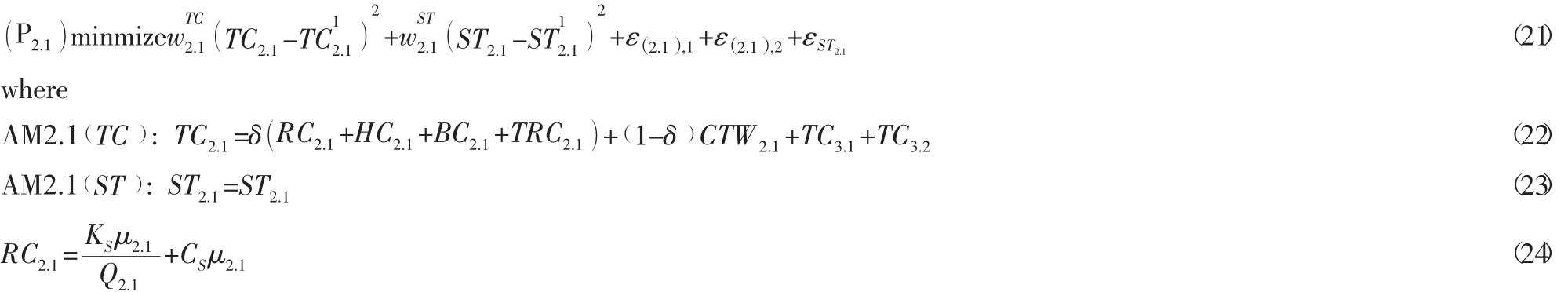
目標函數（21）：TC2.1和ST2.1作為階段2.1的反應。ST2.1同時也是聯系變量。反應目標，是來自階段1.1優化出的結果。由于階段2.1有兩個下游階段，所以具有3個低層級反應與相對應的容限變量相協調。階段2.1的兩個反應必須具有兩個分析模型存在，他們是AM2.1（TC）,AM2.1（ST）。約束條件與階段1.1類似。

2.2.3 零售商層的ATC數學建模

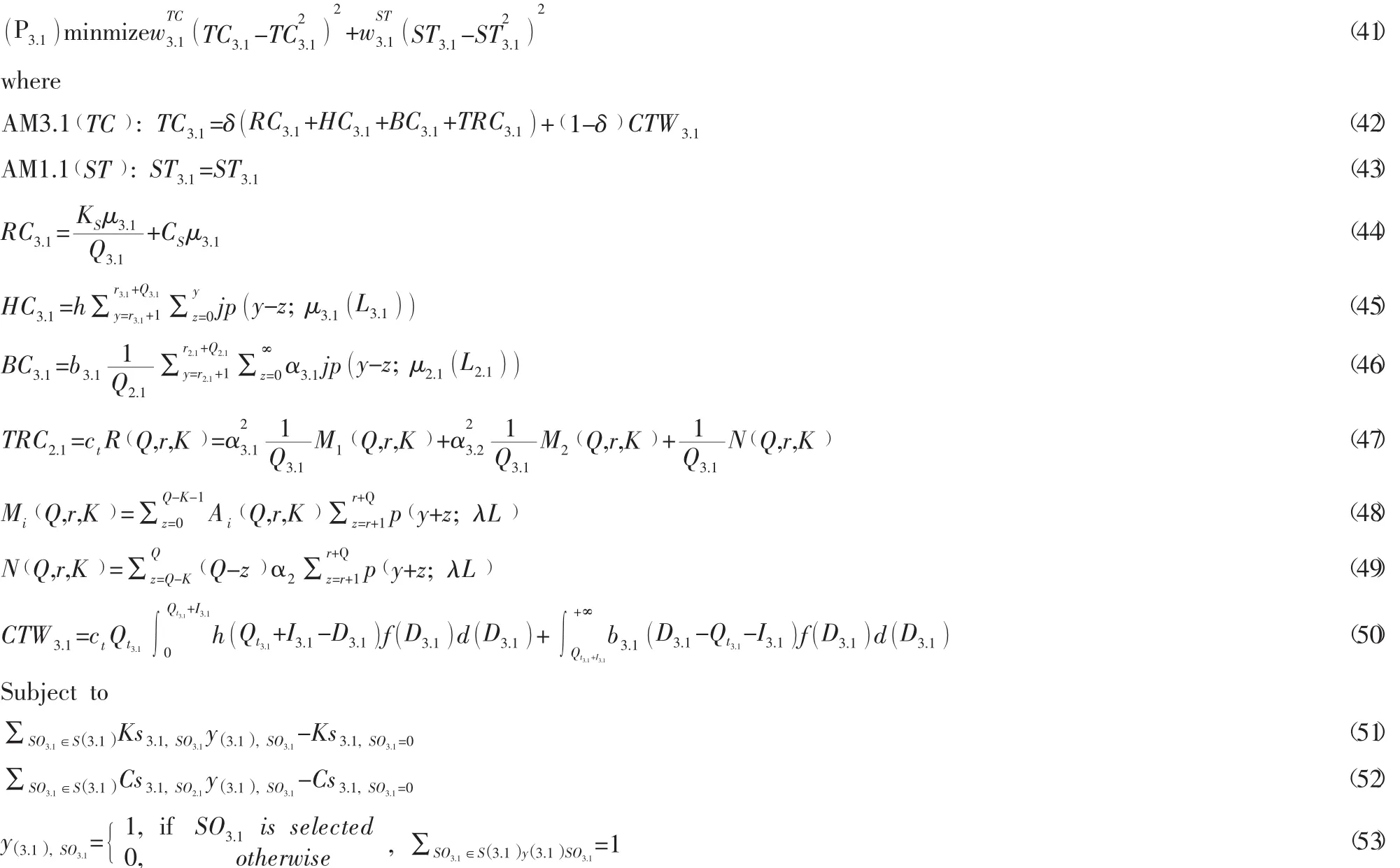
由于階段3.1沒有下游階段，所以容限變量從目標函數中省略，使得只有目標偏差項存在去協調上游階段。由于沒有低層級反應，所以約束條件只有（51） ～（54） 部分。

3 實驗仿真與敏感性分析

3.1 實驗仿真

結合企業在實際運作過程中遇到的常態性真實情況，并經過合理的規范化處理和假設，各節點初始信息設置如表2所示。h=3,Ct=5。本文選擇AIO（All In Once，即傳統一體化優化算法，如GA）和ATC協調這兩種算法對該問題進行求解。計算在CPU主頻為2.5GHz的PC機進行，采用MATLAB 7.11.0軟件進行模擬仿真。最大循環數量為100，偏差權重系數w均為1，ATC最大迭代次數為100。所得結果與AIO優化方法的結果比較如表3所示。

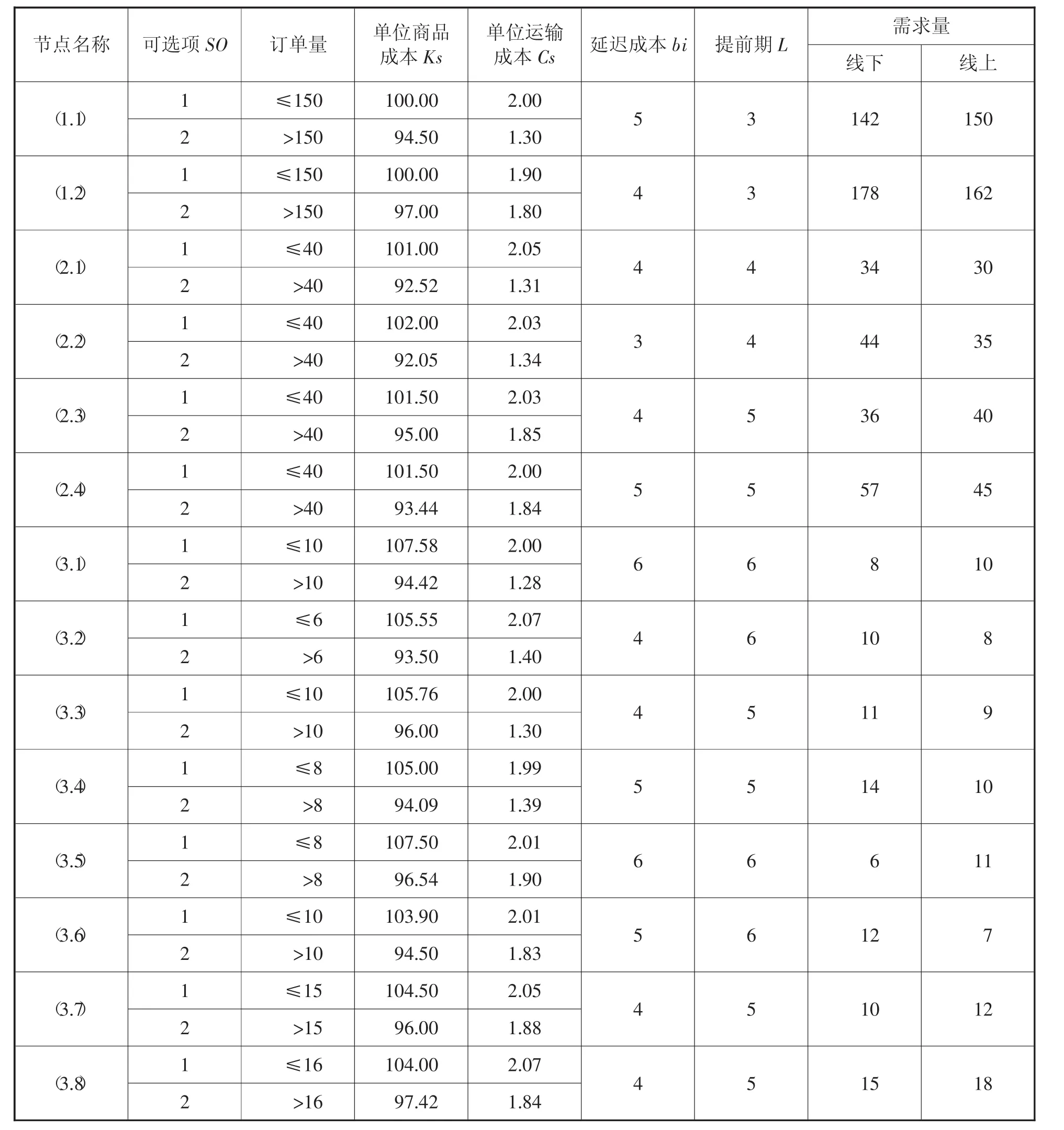
表2 節點初始值

3.2 結果分析

從表3可以看出：

表3 ATC與AIO優化結果

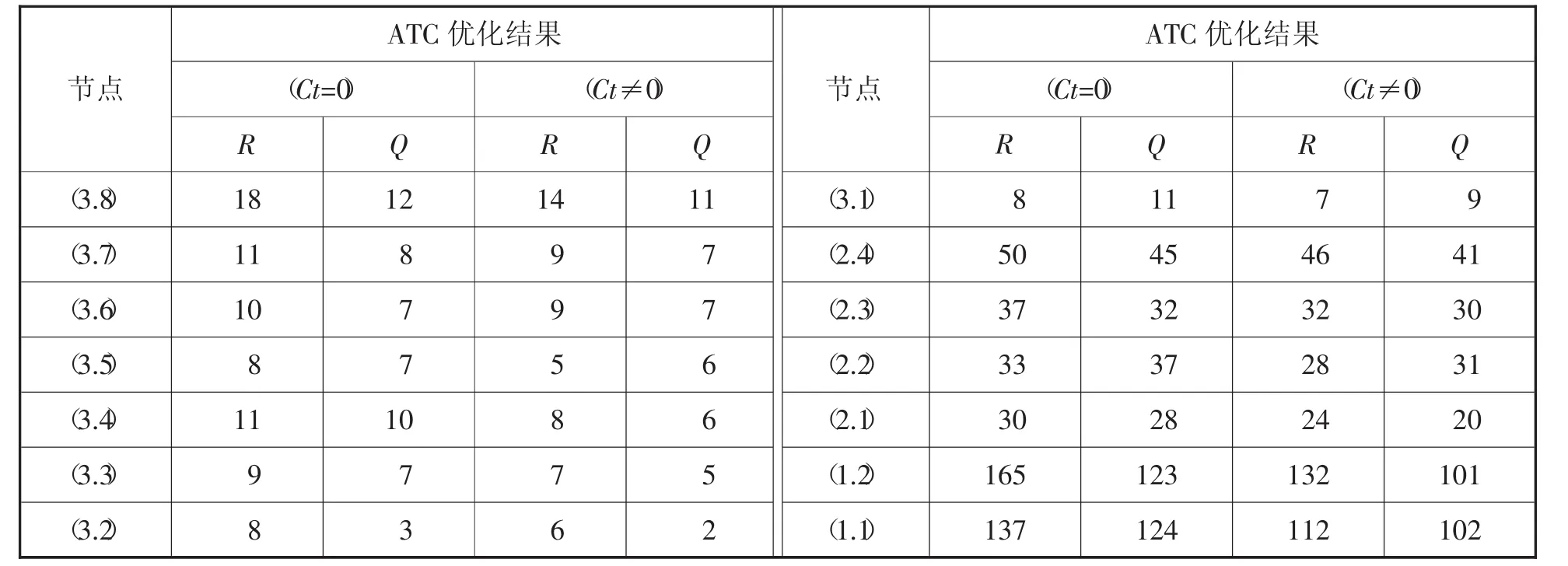
表4 訂貨點與訂貨量輸出結果

（1）本文所使用的ATC優化協調方法與AIO在求解結果準確性方面一致，證實了ATC在求解同層級調撥機制下的雙渠道多級分銷庫存優化配置的有效性。

（3）從優化時間一欄，看出ATC優化的低效率性，AIO的優化時間2分鐘明顯低于ATC的優化時間15分鐘。這是由于運用ATC系統結構分層后，層級之間具有復雜的耦合關系。但是，在本文所研究的問題下，效率的低效性是不可避免的，主要是為了追求企業具有自主決策權。當然，本文是在一個計算機上進行的，大大限制了計算能力。如果當所有的企業同時并行參與計算的話，總的計算能力將會大大提高，并且ATC優化效率明顯高于AIO。

從表4可以看出，無論是訂貨點R還是訂貨量Q，庫存調撥機制下（Ct≠0）的最優值都低于不發生轉運下（Ct=0）的最優值。這主要在于同層級庫存調撥機制不僅在節點內調撥還可以從節點外去轉運，從而更大限度地降低了缺貨可能性。所以庫存調撥機制在保證降低未來缺貨成本的前提下，其訂貨點和訂貨批量設置的相對較低，以此來降低庫存持有成本，進而最終降低庫存總成本。

3.3 敏感性分析

3.3.1 不同的轉運成本對節點總成本和缺貨數量影響

令 ΔTC=（TC（Ct=0）-TC（Ct≠0））/TC（Ct=0），ΔTC=（B（Q,r）（Ct=0）-B（Q,r）（Ct≠0））/B（Q,r）（Ct=0）對比計算轉運 （Ct≠0）與不轉運（Ct=0）條件下對成本TC和缺貨數量B（Q,r）的影響。以零售商層的4個分銷節點為例進行分析。

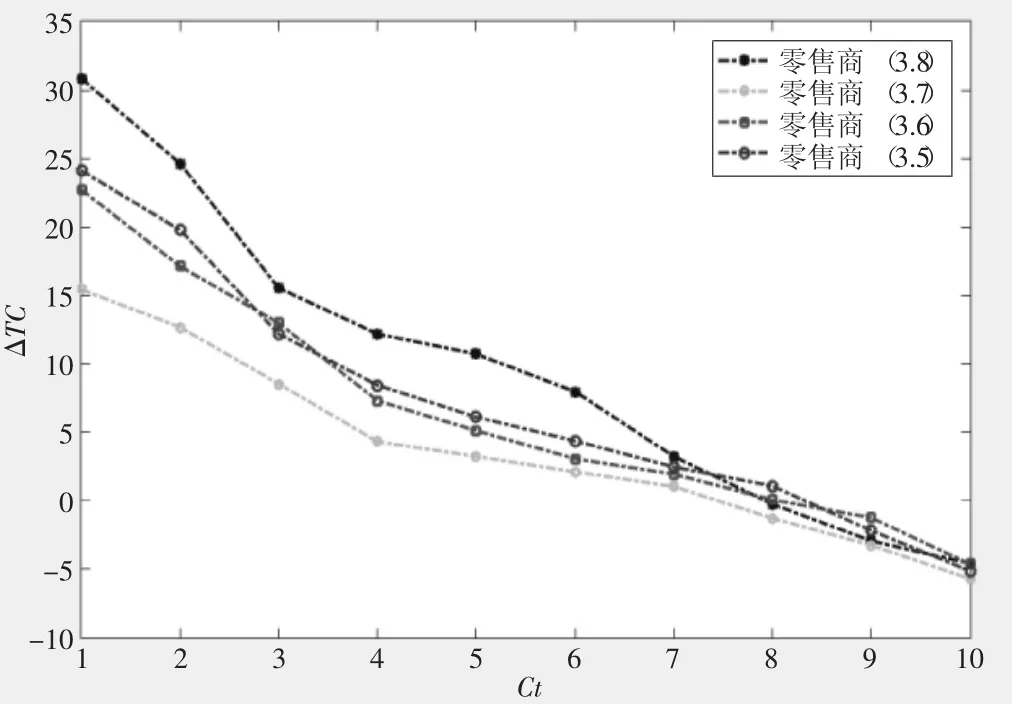
圖3 單位轉運成本對ΔTC的影響

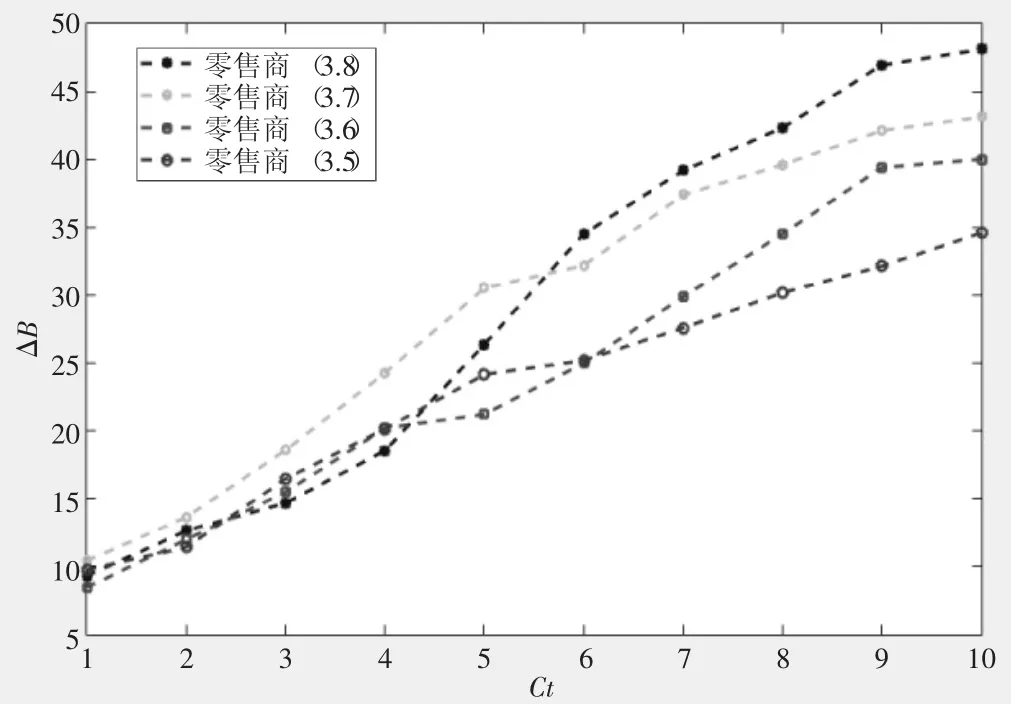
圖4 單位轉運成本對ΔB的影響

從圖3和圖4可以看出，隨著單位轉運成本Ct的增大，在轉運條件下帶來的成本節約逐漸減小，但是發生轉運所帶來的缺貨數量的減少則逐漸增加。當Ct增大到一定程度時，出現了△TC＜0的情況，說明庫存調撥相較于不發生庫存調撥庫存成本會更高。但是，同層級調撥下，即使發生轉運的總成本高于不發生轉運的成本，進行庫存轉運也是有利的。因為需求是隨機的，當一個節點需求突然增大時，可以從另一節點調運，即轉運為節點需求的滿足提供了另一個保障，多個節點相互轉運，能提升整個供應鏈的績效。

3.3.2 不同需求下對節點總成本和缺貨數量影響

圖5 需求量對ΔTC的影響

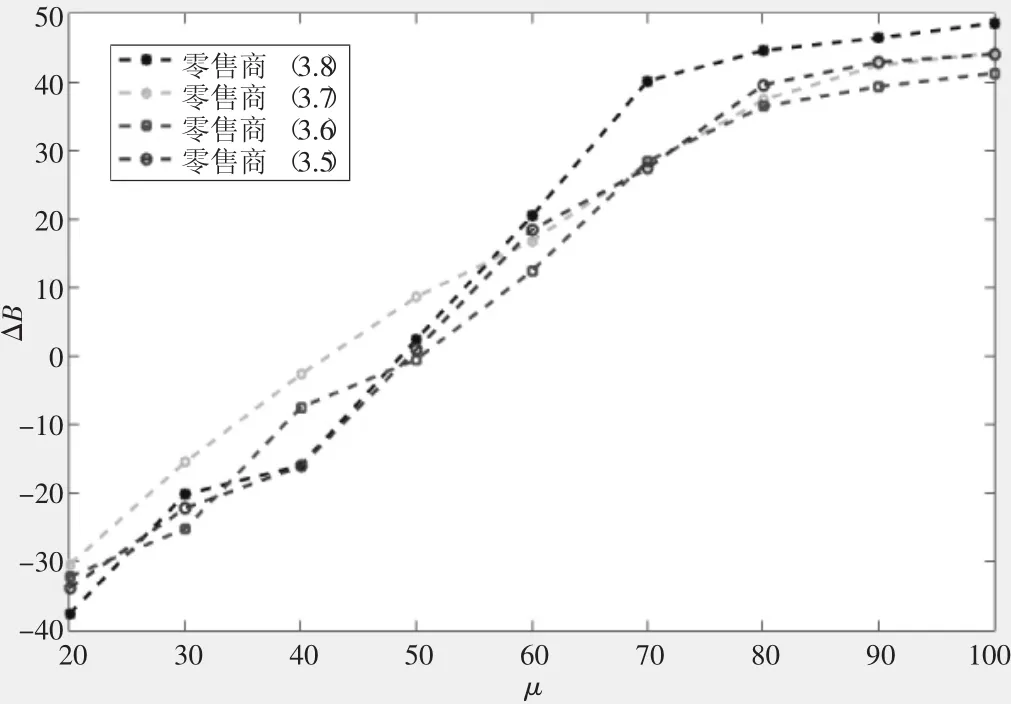
圖6 需求量對ΔB的影響

從圖5和圖6可以看出，隨著需求均值μ的不斷增大，庫存調撥所帶來的成本好處逐漸減少，這是因為需求波動變大（泊松分布均值等于方差）對庫存調撥的影響較小，而使不發生庫存轉運增加的成本更多，因此帶來的相對好處減少。但是，庫存調撥所帶來的缺貨數量的減少逐漸增加，這是因為隨著需求波動變大，單個節點缺貨的概率增加，而庫存調撥的一個顯著特點即是采用轉運來降低缺貨的發生，因此其能減少的缺貨數量增加。

總的來說，無論在哪種情況下，同層級庫存調撥機制總能改善企業的某一項績效指標（如成本、缺貨水平）。

4 結 論

本文對雙渠道多級分銷網絡的運作模式進行了全面分析。面對隨機線上、線下顧客需求，建立同層級庫存調撥機制下的雙渠道多級分銷網絡分布式決策模型。并引入支持層級式優化結構的目標級聯法進行求解。通過與傳統AIO方法結果對比，本文不僅驗證了ATC方法對該類問題的有效性。同時證明了同層級庫存調撥機制對雙渠道多級分銷網絡優化配置的有效性，明顯改善企業的績效目標（成本、缺貨水平）。本文將ATC方法從理論層面擴展到應用層面，為解決實際經營和管理問題提供了一個系統性的分析、建模和求解思路。

本文的主要貢獻有：（1）采用供應鏈配置的思路和方法對雙渠道多級分銷網絡的運作模式進行統一描述，形成了分銷型企業面對隨機的線上、線下顧客需求以及缺貨發生情況下快速配置最優供應鏈的基礎使能框架；（2）在同層級庫存調撥情況下，建立了雙渠道多級分銷分布式決策模型，并將支持層級式協調的ATC優化方法引入供應鏈管理領域進行求解，為該類企業應用層級式協調方法建立現實、可行的優化配置系統提供了使能條件。

本文存在的不足及未來需要擴展的研究如下：（1）模型中參與節點數有限，而實際生活中節點數比較多。（2）本文只考慮了同層級庫存調撥機制，下一步將研究跨層級庫存調撥的多級分銷網絡優化配置問題。