基于SVM-CSO算法的PMSM齒槽轉矩優化
,,,
(廣東工業大學,廣東廣州 510006)
0 引言
隨著永磁材料性能的不斷提高,永磁電機的應用越來越廣泛。永磁體與電樞鐵心相互作用產生的齒槽轉矩是永磁電機固有問題,始終無法避免。齒槽轉矩會引起轉矩波動,進而導致電機振動和噪聲,影響控制系統的精度[1]。
一定程度的永磁體削角既能降低齒槽轉矩與諧波畸變率,又能夠節省永磁體材料,降低成本。文獻[2]利用Maxwell 2D對一款無刷直流電動機在永磁體不同削角的情況進行對比與分析,找出最佳削角。文獻[3]針對表貼式永磁同步電機齒槽轉矩削弱問題,提出了削角長度比例系數的最佳確定方法。文獻[4]對不同程度削角磁極對應的齒槽轉矩進行計算,找到最佳削角位置。文獻[5]推導無槽口電機的削角永磁體齒槽轉矩的解析表達式,并分析了削角對氣隙磁場畸變率的影響。
由于解析法的局限性,文獻[4]很難準確計算永磁體削角后的齒槽轉矩大小。文獻[2]選取24組永磁體削角尺寸進行分析,最終找到的削角位置只是局部優點。本文對比分析25組永磁體削角的情況,并在此基礎上利用支持向量機進行數據擬合,獲得齒槽轉矩目標函數,然后通過縱橫交叉算法求解確定永磁體的最佳削角方式。Maxwell 2D仿真分析結果顯示,本方法是合理有效的,為PMSM磁極削角降低齒槽轉矩提供了一種新思路。
1 齒槽轉矩解析分析
齒槽轉矩是由電樞齒和永磁體之間相互作用力的切向分量引起的轉矩,可表示為不通電情況下,電機磁場能量W對定轉子相對位置角α的負導數。
(1)
根據電樞鐵心導磁率為無窮大的假設,可以得出電機內存儲磁場能量的近似表達式
(2)
式中,Wairgap—氣隙磁場能量;WPM—永磁體存儲的磁場能量;μ0—真空磁導率。
電機的氣隙磁密沿電樞表面有規律分布,可表示為
(3)
利用式(3)整理式(2)可得
(4)
式中,δ(θ,α)、hm(θ)—為有效氣隙長度、沿圓周方向分布的永磁體充磁方向長度和永磁體剩磁。
根據Br(θ)沿圓周的分布情況,對Br2(θ)進行傅里葉分解可得
(5)
(6)
綜合以上各式,并利用三角函數滿足的積分關系式,得到不考慮斜槽時的齒槽轉矩表達式為
(7)
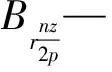
2 永磁體削角設計
2.1 表貼式永磁電機主要技術參數
本文研究對象的主要技術參數見表1。

表1 主要技術參數
2.2 永磁體不同削角分析
本文以永磁體厚度為6mm,寬度為12mm,結構為面包狀,徑向充磁的12槽10極表貼式永磁同步電機為例進行分析。提出永磁體削角方式見圖1,具有兩個自由度,通過改變永磁體邊緣a、b的值,即可得到不同程度的削角永磁體。
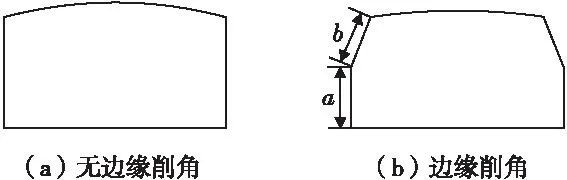
圖1 永磁體的削角方式
永磁體削角后的結構如圖2所示。
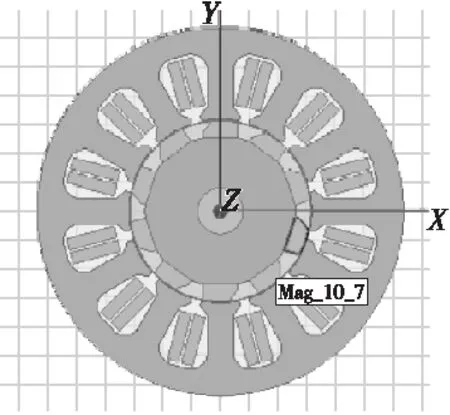
圖2 永磁體削角電機結構圖
根據上述削角方式,按照不同的a、b值對永磁體進行邊緣削角,這里初步選取25組尺寸配合,在Ansys Maxwell 2D中進行仿真分析得到對應齒槽轉矩的值見表2。這里的仿真時間設置為6s,即1個周波。
3 削角尺寸優化
齒槽轉矩與電機參數之間是高度非線性的,難以建立準確的數學關系式。這里選取永磁體邊緣尺寸a、b為設計變量,以齒槽轉矩為目標函數進行優化。本文先采用支持向量機回歸算法對目標函數建模,然后通過縱橫交叉算法對其進行尋優。
3.1 支持向量機回歸
支持向量機(Support Vector Machine,SVM)是統計理論的核心,主要用于解決二值分類問題。SVM在機器學習方面性能優良,其應用已拓展至一類分類問題、多類分類問題及回歸問題。 通過引入核函數,SVM能降低高維問題的維度,并能更好的求解非線性問題。作為統計學習理論中5種常用核函數之一,高斯徑向基核函數目前是SVM的常用選擇。
給定n組樣本數據{xk,yk},k=1,2,Λ,n,通過非線性映射將數據x映射到高維特征空間G,并在G內執行線性逼近操作。對于上述訓練集{xk,yk},基于結構風險最小化原則并使用核函數來求解凸二次規劃,進而獲得支持向量機模型[6]。
(8)
式中,l—支持向量的數量;αi—拉格朗日常數;k(xi,x)—核函數;b—閾值。
取25組尺寸配合中的20組對SVM算法進行訓練,再利用剩下的5組對SVM的擬合效果進行驗證。實際值與預測值的對比情況見圖3。
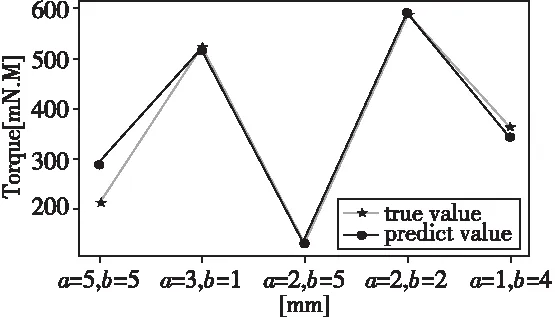
圖3 實際值與預測值對比圖
由上圖可以看出,SVM回歸模型對目標函數的擬合效果較好,可用作CSO算法的適應度函數。
3.2 CSO算法尋優
縱橫交叉算法(crisscross optimization algorithm,CSO)是一種基于種群的隨機搜索算法[7],縱橫交叉在每次種群進化迭代中分別在橫向和縱向產生中庸解,兩種算子交替進行,同時在每次交叉運算后引入競爭操作,保留最優的個體粒子進入下次迭代。CSO的搜索行為由橫向交叉算子、縱向交叉算子和競爭算子一起構成。
兩個不同個體粒子在所有維之間進行的一種算數交叉稱為橫向交叉,假設父代個體粒子X(i)和X(j)的第d維進行橫向交叉,則產生的子代使用以下公式
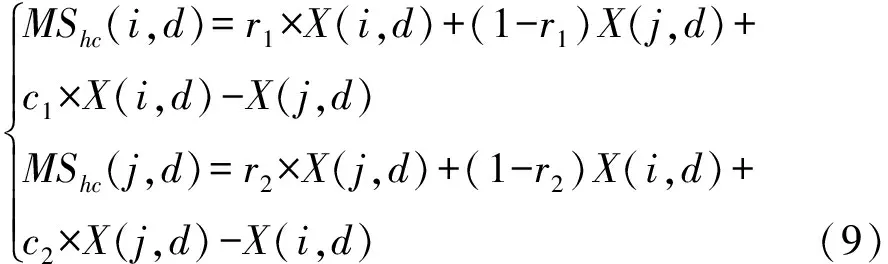
式中,d∈(1,D),r1,r2—(0,1)之間的隨機數;c1,c2—(-1,1)之間的隨機數;X(i,d),X(j,d)—父代種群中個體粒子X(i)和X(j)的第d維;MShc(i,d),MShc(j,d)—通過橫向交叉產生的第d維子代。
所有個體粒子在兩個不同維之間進行的一種算數交叉稱為縱向交叉;假設種群的第d1維和第d2維參與縱向交叉操作,則由以下公式可得到個體粒子X(i)的第d1維和第d2維通過縱向交叉產生的第d1維后代,表示為MSvc(i,d1)
MSvc(i,d1)=r×X(i,d1)+(1-r)X(i,d2)
(10)
式中,d1,d2∈N(1,D),i∈N(1,M),r∈U(0,1)
文中CSO算法以削角尺寸a、b為優化變量,SVM回歸模型為目標函數,其具體參數設定為:種群數量30,最大進化代數100,縱向交叉率0.8。優化結果如圖4所示,最佳削角尺寸為a=3.8477,b=4.3537,對應的Torque=115.29m N·M。
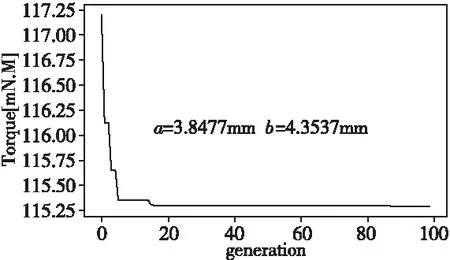
圖4 CSO算法尋優結果
3.3 仿真驗證
將SVM-CSO算法優化過的削角尺寸a=3.8477,b=4.3537代入Maxwell 2D仿真,結果見圖5,經過優化后的齒槽轉矩為115.62mN.M,與算法求解值115.29接近。同時與表2的結果對比,驗證了本方法的準確性。
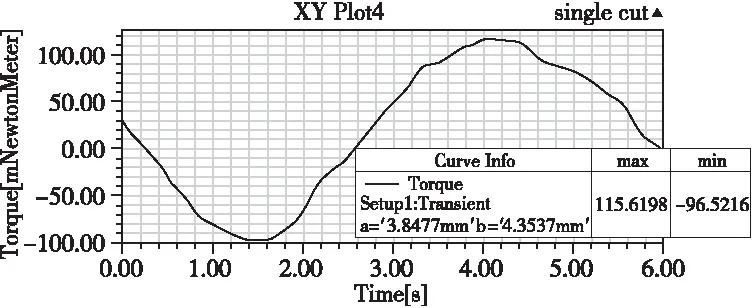
圖5 優化后PMSM齒槽轉矩
4 結語
本文以12槽10極表貼式永磁同步電機為例,使用Ansys軟件對永磁體不同位置削角時的齒槽轉矩進行仿真分析。以25組數據為樣本空間,通過支持向量機算法建立目標函數,并使用縱橫交叉算法求解獲得最優的削角尺寸,最后應用有限元仿真軟件驗證。研究結果表明SVM-CSO算法模型的有效性及準確性,為電機結構參數優化提供了新思路。

