一種直驅永磁電機分數槽繞組的設計與分析
(中車永濟電機有限公司特種產品開發部,陜西西安 710018)
0 引言
隨著近年來電力電子的快速發展,其拓撲結構不斷變化,永磁電機的應用領域也越來越寬廣。特別是對于一些去除齒輪箱的直驅系統,電機與負載直接相連,因系統結構簡單和總損耗減少,直驅永磁電機越來越被市場看好。
當永磁電機旋轉時,由于定子鐵心開槽導致主磁路中磁阻發生變化,由永磁體與定子齒間相互作用從而產生了齒槽轉矩[1]。齒槽轉矩的產生導致永磁電機的轉矩波動,使電動機運行時產生振動,并使電機的可控性變差。因此對于永磁電機,很有必要對減少齒槽轉矩采用有效的措施[2]。
對于內置式直驅永磁電機,可以通過采用極數與定子槽數配合、增大氣隙長度、定子斜槽或轉子斜極、氣隙磁密波形優化等多種方法來實現[1]。本方案通過采用雙層短距分布式分數槽繞組,有效的削弱了齒諧波和齒槽轉矩,使反電勢波形諧波含量減少,使電機負載運行時轉矩波動達到工業使用要求。
1 常用交流繞組
電機定子中的交流繞組一般原則是[2]:(1)由繞組合成的磁動勢及電動勢在空間波形分布上盡量接近正弦波形;(2)其基波磁動勢和基波電動勢力求最大;(3)既要節省銅材也要把損耗控制在合理范圍內;(4)對多相繞組其各相磁動勢和電動勢要對稱,電阻和電抗要平衡。
對于永磁電機,其電樞繞組主要是與由永磁體產生的主磁通相對運動而感生電動勢。通常而言,按每極每相槽數分類,可以分為整數槽和分數槽繞組;按槽內線圈邊層數分類,有單層繞組和雙層繞組;按繞組線圈的組成形式分類,可以分為硬繞組和散繞組。
1.1 整數槽與分數槽
每極每相槽數為整數時為整數槽繞組,而q不為整數時就是分數槽繞組。這兩種繞組均可用槽電勢相量圖星形圖分析。分數槽繞組的基本對稱條件為:Q0/m=整數(其中Q/t、Q為定子槽數、t為極對數p與槽數Q的最大公約數)。其值為偶數時,線圈可接成單層和雙層繞組,采用雙層繞組時最大并聯支路數amax為2t;其值為奇數時,一般采用雙層繞組,其最大并聯支路數為amax為t[2]。
1.2 單層繞組與雙層繞組
單層繞組為每槽放一個繞組的線圈邊,其中有同心式、等元件式和交叉鏈式等不同連接方式[3],繞組由線圈個數和節距相等或不等的數個線圈構成。其優點有槽內無層間絕緣,槽利用率高;線圈數比雙層繞組少一半,但同時因不能做成短距繞組,從而無法改善磁場波形。
雙層繞組每槽分為上下兩層,分別放置兩個不同線圈的直線邊。雙層繞組的結構和尺寸均相同,連線整潔、美觀,有利于散熱和增加機械強度。同時可通過選擇短距來改善電樞磁場波形,不足之處就是絕緣材料多,嵌線麻煩。
1.3 硬繞組與軟繞組
散繞組由圓電磁線束包而成,其漆膜比較薄,耐沖擊力差,很容易受到損傷,但結構簡單、易繞制、端部短、用銅少、電阻和漏抗小。與其配套的半閉口槽槽口相對較小,有利于降低齒諧波幅值、均衡氣隙磁場;硬繞組由數個獨立的線圈構成,一般由扁銅線繞制而成,易保持一定的形狀,根據實際情況分為多層結構,其機械性能、電性能、熱性能和化學性能較散繞組均有不同程度的提高,是提高電機耐電壓脈沖應力最好的繞組型式之一。但相對地,其端部長、用銅量多、銅耗大、電阻和漏抗大[4]。
2 分數槽繞組
對于直驅永磁電機,其極數較大,如果采用整數槽結構,一般按每極每相槽數q≥2設計,其定子槽數必然很大,定子沖片開槽和嵌線都很困難。通過綜合對比,本方案采用雙層短距分數槽繞組結構,分數槽繞組永磁電機不僅具有永磁同步電機特有的優點,還可以有效的削弱齒槽諧波,減弱齒槽轉矩,減小電動勢和電樞磁動勢諧波分量幅值。其可以采用很少的槽數來實現與槽數很多的整數槽繞組的分布性能,同時采用分數槽在工藝上因為槽少而易于實現。
因分數槽繞組含有一系列次數與基波不成整數倍的諧波,其具有較大的諧波漏抗,但其在同步電抗中占得比例很小,只需注意與基波成奇數倍的諧波。分數槽繞組不能抵消的最低次數諧波為槽數和極數的最小公倍數次諧波[2],對于本方案,其部分參數如表1所示,采用的是20極66槽結構,不能消除的最小諧波次數是660次,也既是齒諧波基波的10次諧波,而齒諧波基波以及2~9次諧波都已被抵消。另外值得注意的是分數槽繞組會產生幅值很高的磁動勢諧波,每極每相槽數q分母不為2的時候會產生次諧波。因此,選取合理的極槽配合是直驅永磁電機設計的關鍵。
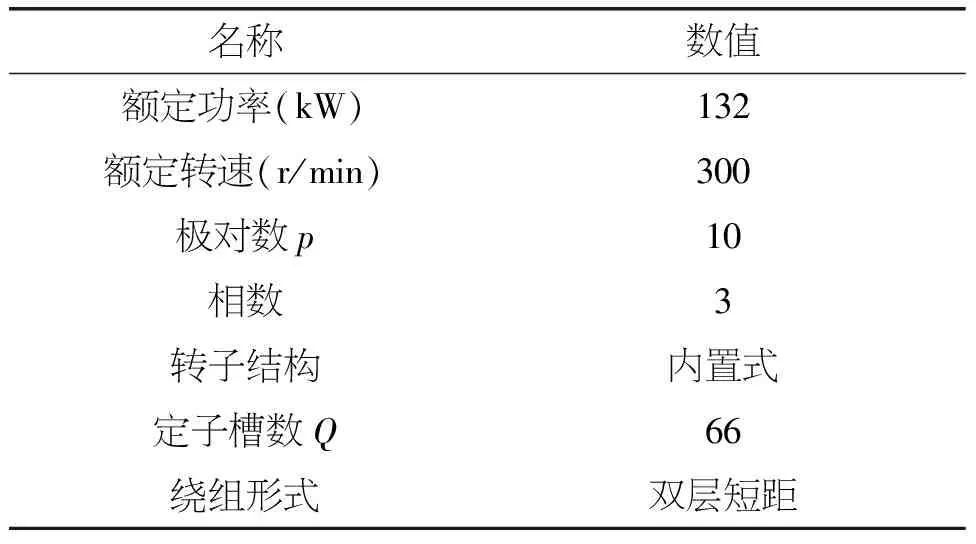
表1 直驅永磁電機部分參數
極對數p與槽數Q的最大公約數為t=2,其由p0=p/t=10/2=5對極下的Q0=Q/t=66/2=33個槽電動勢相量組成一個完整的槽電動勢星形圖,如圖1所示,共有2個重疊的基本星形,按槽號順序列出的各槽所屬相帶見表2。
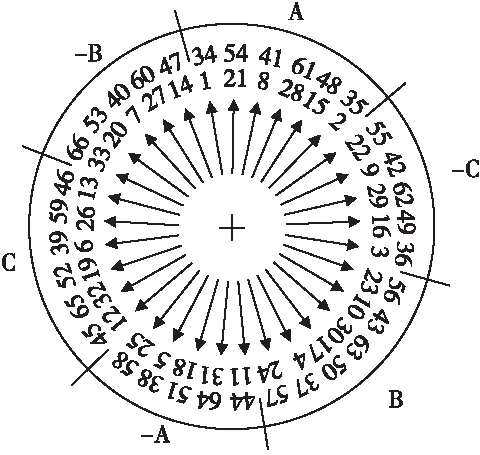
圖1 槽電動勢相量星形圖
表2中一相繞組所在的槽數為有規則的數列循環,其數列為2111111111,由一個2和9個1組成。其值計算方式[2]為:(1)把每極每項槽數q表示為q=b+c/d,式中b為整數,c/d為不可約的分數;(2)一個循環數列共有d個數,其中c個為大數,大數為b+1,d-c個為小數,小數為b。
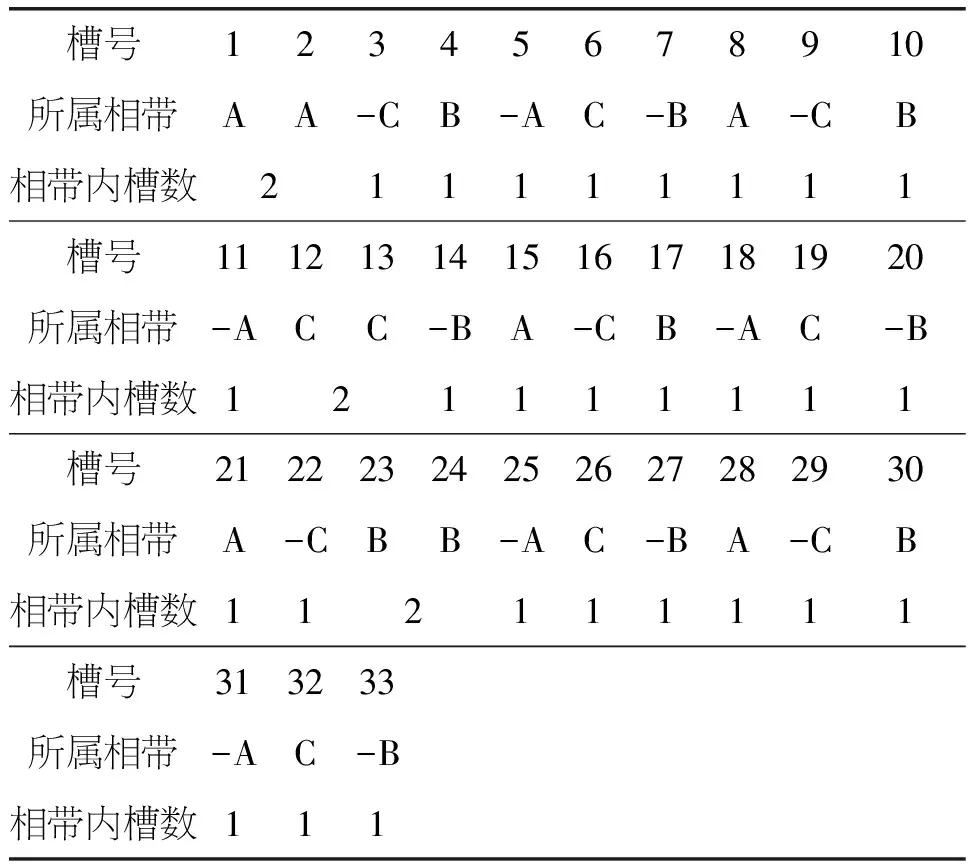
表2 分數槽繞組槽號與相帶(因t=2,取槽數一半)
3 繞組參數計算及有限元分析
針對直驅永磁電機,對采用分數槽集中繞組和不同短距系數的雙層短距分布式繞組進行了對比分析:計算了其繞組系數及各次諧波的含量;利用有限元法對比分析了永磁電機的空載線反電勢和轉矩波動;與采用斜槽結構的整數槽設計方案進行了方案對比。
3.1 分數槽繞組系數計算
3.1.1 分布系數和短距系數[2]
本方案采用分數槽繞組(q=b+c/d=N/D,其中D≠1,N和D沒有公約數),其基波和v諧波的分布系數為
(1)
(2)
基波和次諧波的短距系數為
(3)
(4)
式中,Z—定子槽數;y1—線圈節距。
kdp為繞組系數,是分布系數kd和短距系數kp的乘積。kdpv為對應于次諧波的繞組系數
kdpv=kdvkpv
(5)
3.1.2 永磁感應電勢繞組系數計算
感應電勢中的諧波對電機運行產生諸多不良影響,因此需要盡可能減少諧波含量和削弱諧波幅值。主要有采用短距線圈和非等元件繞組等方法[5]。雙層繞組一般通過選用不同的節距來消除5次、7次等各次諧波,從而改善電動勢和磁動勢波形。
在定子槽數比較小時,節距按式y1=Z/2p選擇(y1=Z/2p為向下取整,即取比Z/2p小的最大整數),即線圈跨距接近極距,其基波繞組系數大[6]。通過表3也可看出,采用最大短距節距(即y1=3)時其基波繞組系數最大;采用分數槽集中繞組(即y1=1)時,其電樞反應磁動勢諧波含量很高,但5、7次諧波含量最小。
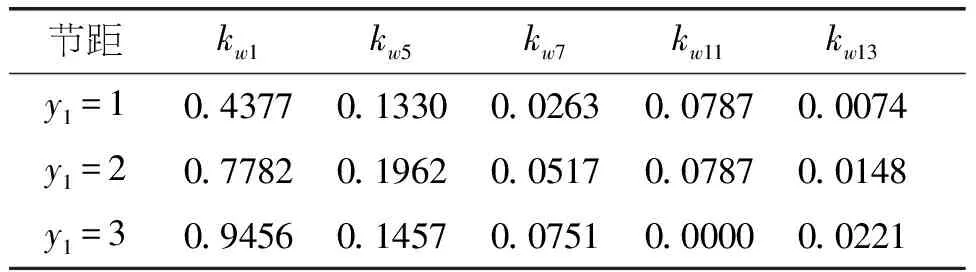
表3 采用不同節距時繞組諧波系數
3.2 有限元分析
為了得到永磁電機準確的性能參數,需要對電機磁場進行數值計算與分析。而磁場數值方法有有限元法、有限差分法、邊界單元法等,因有限元法特別適合邊界形狀復雜、材料存在非線性等磁場問題,其應用最為廣泛[1]。
3.2.1 不同短距系數的分數槽方案對比
利用有限元法對采用不同短距系數的分數槽繞組直驅永磁電機,分別從空載反電勢和轉矩波動兩個方面進行了對比分析。
(1)空載線反電動勢
空載反電動勢是永磁電機一個非常重要的性能參數,對電機的功率因數影響很大。其不僅決定永磁電機所處是增磁還是去磁狀態,并對電機的瞬態和靜態性能有很大的影響[7]。
對于直驅永磁電機,電機采用Y接,所以3及3的倍數次諧波空載線感應電動勢為零。采用不同節距時,其諧波含量見表4。
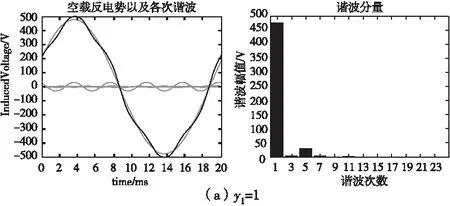
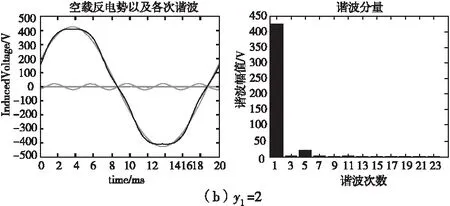
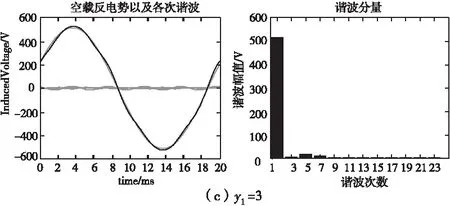
圖2 采用不同節距時線反電動勢波形及諧波分布
(2)轉矩波動
直驅永磁電動機運行時,一個很重要的性能指標就是轉矩波動,通常轉矩波動由上下波動值對其平均值的百分數表示,其定義公式為[2]
式中,ΔT—轉矩波動;Tmax—最大轉矩;Tmin—最小轉矩。其對比分析見表5,可以看出,當y1=1其轉矩波動最大,y1=2轉矩波動最小,但三種方式均<5%。
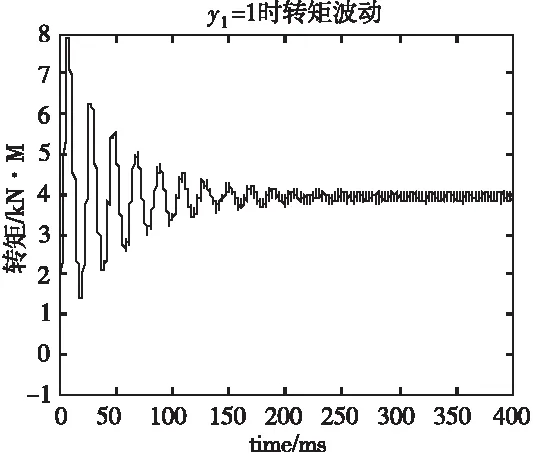
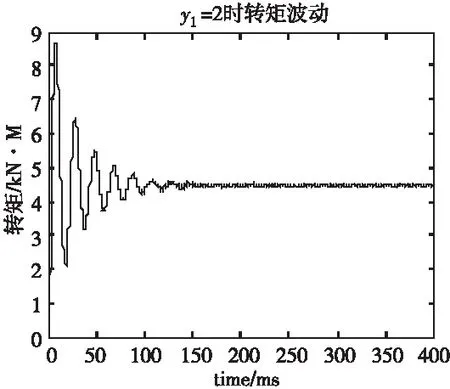

圖3 采用不同節距時負載轉矩波動
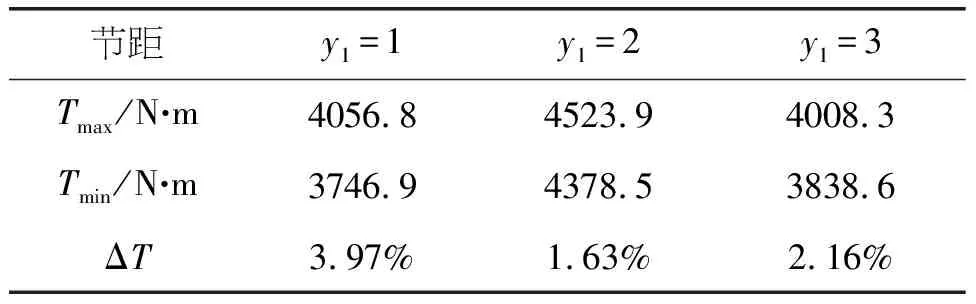
表5 采用不同節距時線反電動勢諧波含量
3.2.2 與整數槽斜槽方案的對比
整數槽方案與采用分數槽不同之處在于其每極每相槽數為整數,為了削弱齒槽轉矩而采用了定子斜槽結構,其對比方案見表6。同時從空載氣隙磁密、空載反電勢、齒槽轉矩和轉矩波動等方面對比分析了分數槽與整數槽斜槽結構的優劣。

表6 分數槽與整數槽部分方案對比
(1)空載氣隙磁密
直驅永磁電機需要正弦波分布的空載相反電動勢,如果氣隙磁密分布均勻,則永磁電機可以得到正弦性良好的空載相反電動勢,相反,則進一步影響電機的運行性能。
采用整數槽時其氣隙磁密諧波含量遠高于采用分數槽繞組結構時的諧波總含量見表7。
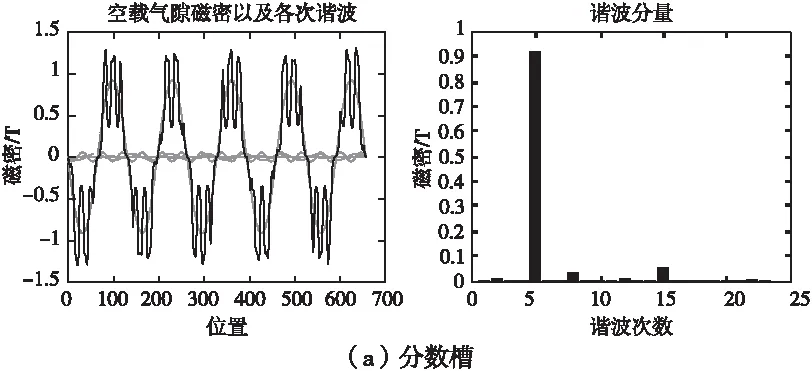
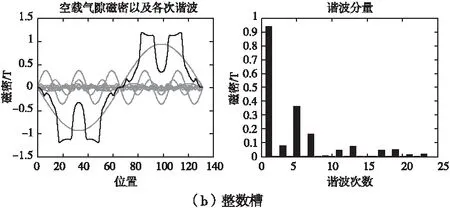
圖4 空載氣隙磁密波形及諧波分布
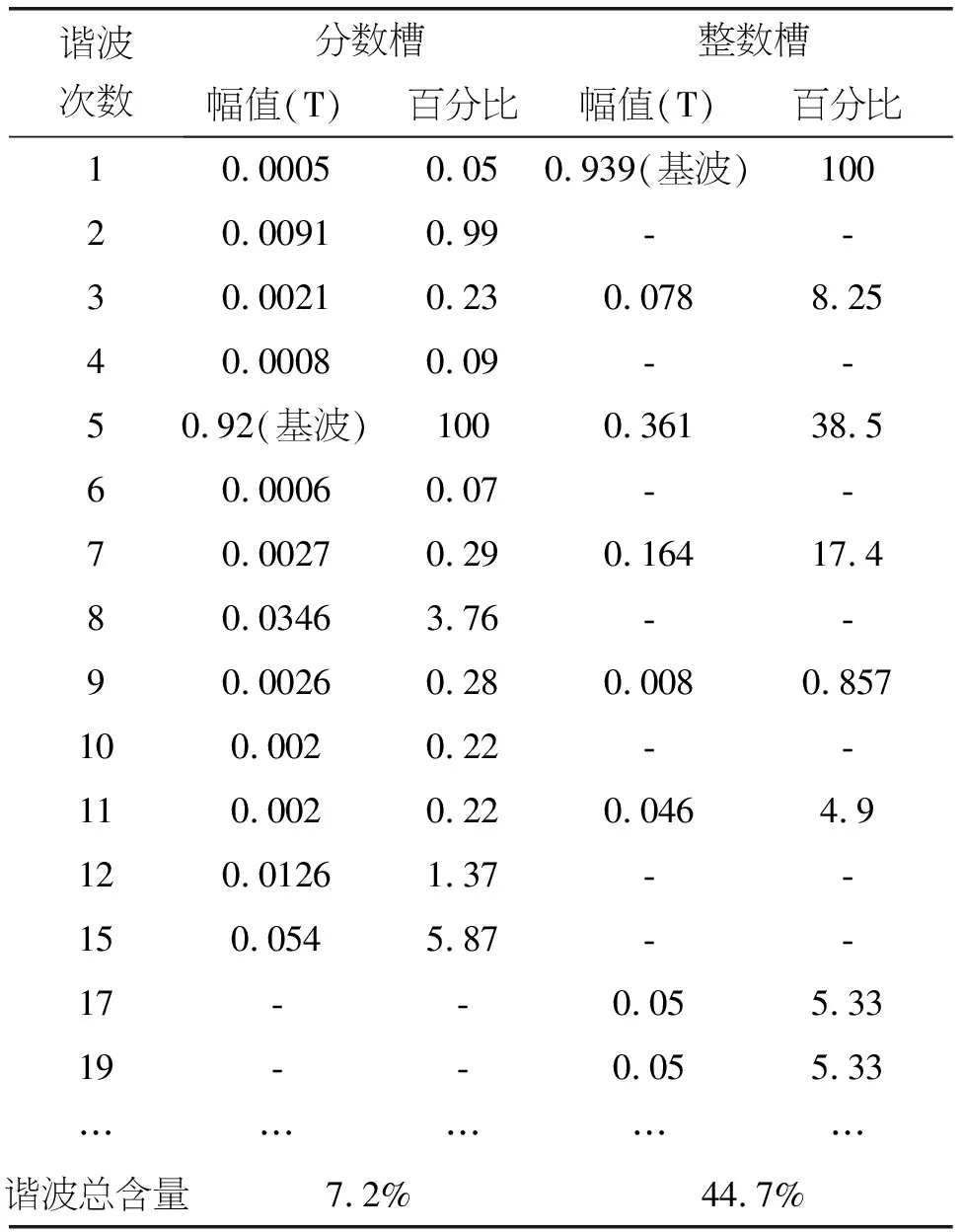
表7 空載氣隙磁密各次諧波幅值及百分比
(2)空載反電勢
對于直驅永磁電機,低速平穩性是一個很重要的指標,而影響其性能的主要因素為永磁電機的脈動轉矩,包括紋波轉矩和齒槽轉矩[1]。其紋波轉矩就是由電動勢或電流非正弦引起的。因此,當電機處于空載時,對其反電勢進行了對比分析,結果見表8所示。可以看出,分數槽優于整數槽結構。
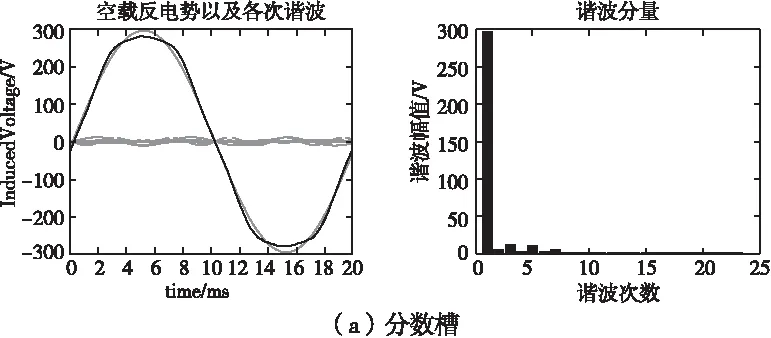
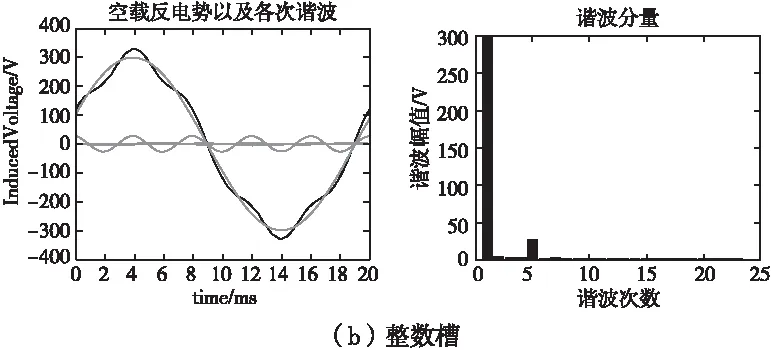
圖5 空載相反電勢波形及各次諧波分布
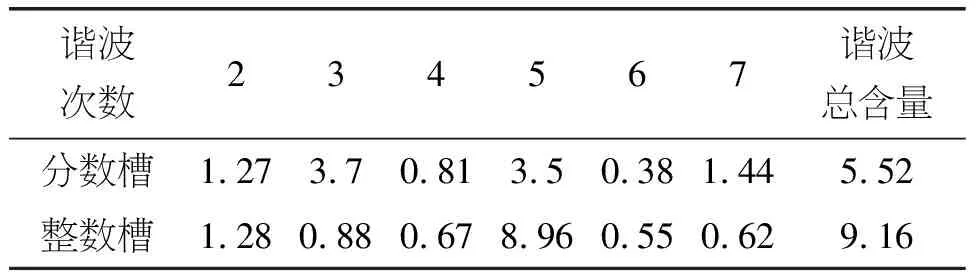
表8 分數槽與整數槽相反電動勢諧波含量(%)
(3)齒槽轉矩
由圖6可知,分數槽齒槽轉矩波動最大值為18 N·m,整數槽斜槽后其波動最大值為80 N·m,相差4.5倍,可見,分數槽具有明顯的優勢。
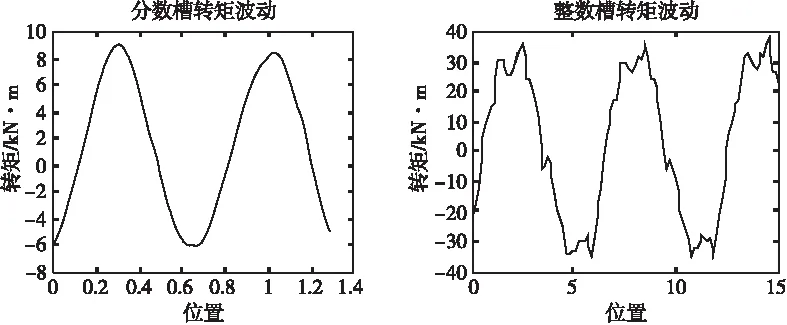
圖6 齒槽轉矩波形
(4)轉矩波動
電機負載時,其轉矩波動如圖7所示。表9中結果顯示,采用分數槽結構較整數槽時減少了6.67%的轉矩波動。
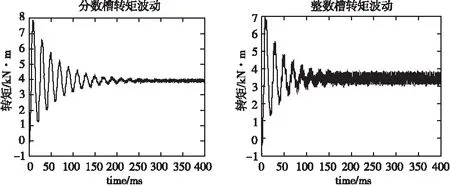
圖7 負載轉矩波動

表9 轉矩波動數值對比
4 樣機試制
圖8為現場嵌線時線圈成型圖和總裝完成后送往試驗的圖片,可以觀測出鐵心線圈整潔、緊湊。同時,隨著試驗的通過,最終驗證了本方案選擇的合理性。

圖8 鐵心線圈及直驅永磁電機
5 結語
通過選取合適的分數槽雙層短距繞組,有效的削弱了永磁直驅電機的齒諧波和齒槽轉矩,降低了電動勢和電樞反應磁動勢諧波分量幅值。通過分析采用不同短距系數分數槽繞組的優劣,與整數槽斜槽結構的對比,又同時從工藝角度出發,驗證了直驅永磁電機極槽配合選取的合理性。
盡管分數槽集中繞組和整數槽分布繞組應用廣泛,但需要對應一定的極槽配合:對于每極每相槽數為真分數(即極槽數相近配合)的時候,利于采用分數槽集中繞組;對于q為假分數的時候,需要根據實際情況對比選擇合適的方案。

