AR模型的譜分辨率及小信噪比下的性能分析?

劉晞遠(yuǎn) 胡昊穎 吳 珊 郭萬里

（西安電子科技大學(xué)通信工程學(xué)院 西安 710126）

1 引言

譜估計(jì)的主要方法有非參數(shù)化法和參數(shù)化法，或稱經(jīng)典譜估計(jì)方法和現(xiàn)代譜估計(jì)方法。經(jīng)典譜估計(jì)方法是以傅立葉變換為基礎(chǔ)的，雖然具有計(jì)算效率高的優(yōu)點(diǎn)，但它沒有將信號的可用信息結(jié)合到估計(jì)過程中，有著頻率分辨率低和旁瓣泄漏嚴(yán)重的固有缺點(diǎn)［1］。現(xiàn)代譜估計(jì)的一個(gè)重要方法就是將被觀測過程表示為一個(gè)AR過程，通過對過程參數(shù)的估計(jì)，可以直接計(jì)算其功率譜密度。該方法可以獲得更精確，頻率分辨率更高的譜估計(jì)［2］。

2 AR模型現(xiàn)代譜估計(jì)

2.1 AR模型的建立［3］

現(xiàn)代譜估計(jì)的方法一般按照以下三個(gè)步驟進(jìn)行：1）為被估計(jì)的隨機(jī)過程確定或選擇一個(gè)合理的模型，這種選擇可能是基于有關(guān)信號是如何產(chǎn)生的先驗(yàn)知識；2）根據(jù)已知觀測數(shù)據(jù)估計(jì)模型的參數(shù)；3）用估計(jì)得到的參數(shù)代入模型參數(shù)估算功率譜。

一個(gè)AR過程x(N)可以表示為單位方差白噪聲驅(qū)動的全極點(diǎn)濾波器的輸出。p階AR過程的功率譜是［4］

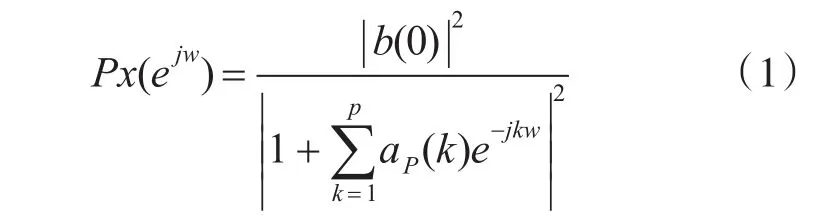
在實(shí)際應(yīng)用中，常需根據(jù)信號的有限個(gè)取樣值來估計(jì)AR模型的參數(shù)，求其參數(shù)的方法主要有：Yule-Walker法或自相關(guān)法；協(xié)方差法；Burg法；修正的協(xié)方差法。以上方法都可以用由時(shí)間平均代替集合平均的最小平方準(zhǔn)則推導(dǎo)得到。

2.2 AR模型參數(shù)估計(jì)的典型算法

2.2.1 自相關(guān)法［5］

自相關(guān)法是直接估計(jì)AR參數(shù)。用最小平方時(shí)間平均代替集合平均準(zhǔn)則，有

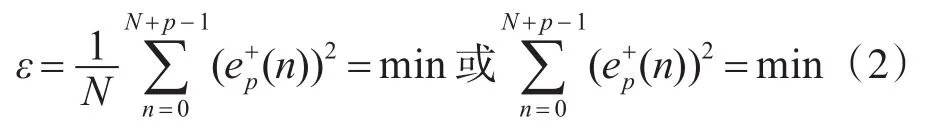
自相關(guān)法的計(jì)算效率高，且能保證預(yù)測誤差是最小相位的，但數(shù)據(jù)兩端要附加零取樣值，實(shí)際上等效于數(shù)據(jù)加窗，這將使參數(shù)估計(jì)的精度下降。特別是當(dāng)數(shù)據(jù)段很短的時(shí)候，加窗效應(yīng)就更為嚴(yán)重。

2.2.2 Burg算法［6］

Burg法與自相關(guān)法不同，它不直接估計(jì)AR參數(shù)，而是先估計(jì)反射系數(shù)，然后利用Levinson遞推算法由反射系數(shù)求得AR參數(shù)。Burg法在希望利用已知數(shù)據(jù)段兩端以外的未知數(shù)據(jù)的同時(shí)，又設(shè)法保證了使預(yù)測誤差濾波器是最小相位的［7］。因此，Burg算法是基于 Levinson-Durbin［8］遞推公式，對誤差序列的最小化準(zhǔn)則進(jìn)行修正的AR模型參數(shù)估計(jì)法。

Burg法首先要估計(jì)反射系數(shù)，使用的準(zhǔn)則是前項(xiàng)和后項(xiàng)預(yù)測誤差功率估計(jì)的平均值最小準(zhǔn)則（預(yù)測誤差功率估計(jì)用時(shí)間平均代替集合平均）。因此，Burg法估計(jì)反射系數(shù)的準(zhǔn)則表示

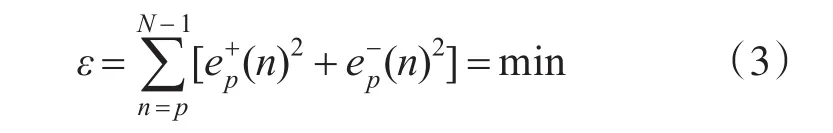
該式的前項(xiàng)和后項(xiàng)預(yù)測誤差濾波器的工作都是在數(shù)據(jù)段上進(jìn)行的（數(shù)據(jù)段兩端不需要補(bǔ)充零）。

2.3 AR譜估計(jì)的異常現(xiàn)象

1）虛假譜峰［7］

如果自相關(guān)函數(shù)的取樣值或反射系數(shù)值的估計(jì)沒有誤差，那么AR（p）模型參數(shù)的估計(jì)值在理論上應(yīng)該為

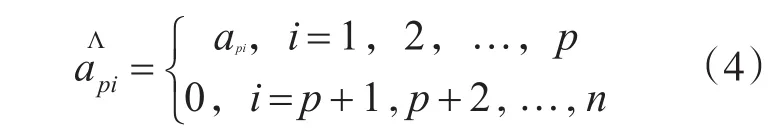
式中，api是AR（p）模型的精確參數(shù)值，是其估計(jì)值。但是實(shí)際上自相關(guān)函數(shù)或反射系數(shù)的估計(jì)是有誤差的，一般來說，這就有可能使得對于大于p的i值有≠0，相應(yīng)的將會產(chǎn)生n-p個(gè)額外的極點(diǎn)。若這些額外的極點(diǎn)出現(xiàn)在單位圓附近，就會形成虛假的譜峰。

2）譜線分裂［8］

如果要估計(jì)的隨機(jī)過程是由一個(gè)正弦信號疊加噪聲所構(gòu)成，那么AR譜估計(jì)中譜峰出現(xiàn)的位置與正弦信號的初相位有著密切關(guān)系。而對于某些算法，還會觀察到AR譜估計(jì)中存在兩個(gè)靠的很近的譜峰，似乎在隨機(jī)過程中還存在著另一個(gè)正弦信號。這一現(xiàn)象稱為譜線分裂。

其中，Burg算法可以觀察到AR譜估計(jì)出現(xiàn)譜線分裂現(xiàn)象。由經(jīng)驗(yàn)總結(jié)出，在以下幾種情況下最容易發(fā)生譜線分裂現(xiàn)象［9］：（1）高信噪比；（2）正弦分量的初始相位為45°的奇數(shù)倍；（3）數(shù)據(jù)序列長度為正弦分量1/4周期的奇數(shù)倍；（4）估計(jì)的AR參數(shù)的數(shù)目與數(shù)據(jù)的個(gè)數(shù)相比占有較大的百分比；（5）虛假譜峰常伴隨產(chǎn)生譜線分裂現(xiàn)象，這與數(shù)據(jù)記錄長度太短有關(guān)。因此，增加數(shù)據(jù)記錄長度，這種現(xiàn)象便隨即消失。

2.4 模型階數(shù)的選擇［10］

在AR譜估計(jì)中，模型階次的選擇是一個(gè)關(guān)鍵問題。階次太低將會導(dǎo)致過于平滑的譜估計(jì)結(jié)果，頻率分辨率過低；而階次太高，將會產(chǎn)生虛假譜峰，并且估計(jì)的方差也會增大。文中采用最終預(yù)測誤差準(zhǔn)則（FPE）判斷最優(yōu)階次。該準(zhǔn)則的計(jì)算公式為［11］

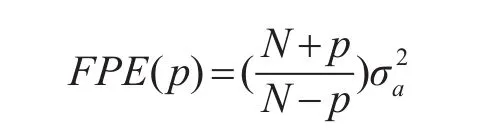
其中：N為數(shù)據(jù)點(diǎn)數(shù)；p為待估計(jì)參數(shù)，對AR（n）模 型 ，p=n；σa2為模型殘差。

文獻(xiàn)指出，估計(jì)階次的上界L與樣本長度N之間的關(guān)系為［12］，但文中既沒有給出理論推導(dǎo)，也沒有給出實(shí)際驗(yàn)證。通過實(shí)驗(yàn)研究表明，將樣本長度的均方根值作為滾動軸承AR模型的定階上界，可以得出滿意的AR模型分析結(jié)果。

3 Levinson算法和Burg算法下的AR模型的譜分辨率性能分析

AR模型功率譜估計(jì)性能，可以用Matlab仿真實(shí)現(xiàn)。本文仿真選取采樣點(diǎn)數(shù)為256（中等長度的數(shù)據(jù)），采樣頻率為100的信號。為了深入研究兩種算法的譜分辨率性能，采用下列自編程序代替Matlab內(nèi)置函數(shù)在Matlab上進(jìn)行了仿真，如下：

3.1 預(yù)測階次p對兩種算法譜分辨率的影響

1）預(yù)測階次p對Levinson算法仿真結(jié)果的影響

使用Matlab仿真了F1=20Hz；F2=21Hz條件下不同頻率對應(yīng)的功率譜圖，如圖1～圖5所示。

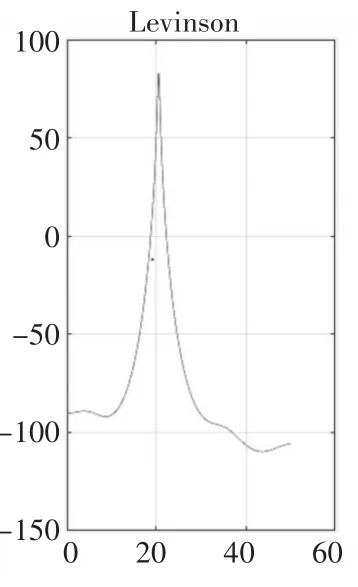
圖1 p=5時(shí)

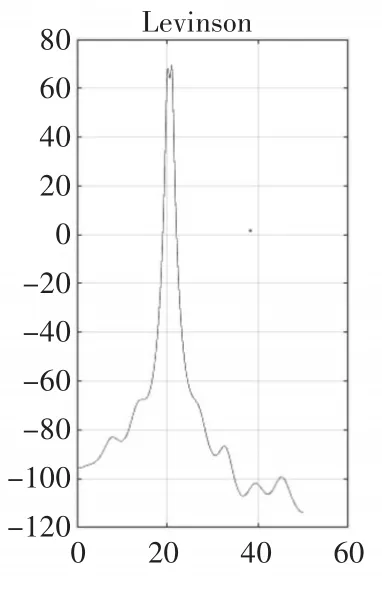
圖2 p=10時(shí)

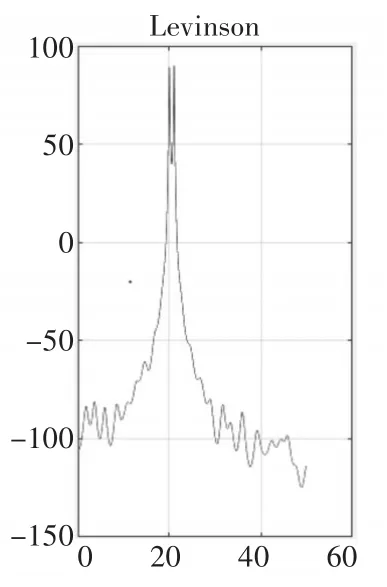
圖3 p=20時(shí)

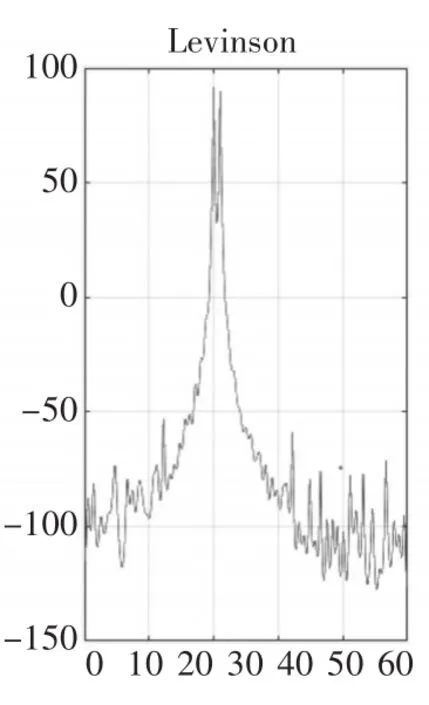
圖4 p=56（N/4）時(shí)

圖5 p=128（N/2）時(shí)

仿真結(jié)果顯示：Levinson算法的分辨率較低，在p=20時(shí)分辨率才能達(dá)到1Hz；階次越大，譜線的虛假譜峰現(xiàn)象越嚴(yán)重，圖5中最大虛假譜峰已經(jīng)達(dá)到-50dB；Levinson算法的仿真沒有出現(xiàn)譜裂現(xiàn)象。

2）預(yù)測階次p對Burg算法的影響

使用Matlab仿真了F1=20Hz；F2=21Hz條件下不同頻率對應(yīng)的功率譜圖，如圖6～圖10所示。

圖6 p=5時(shí)

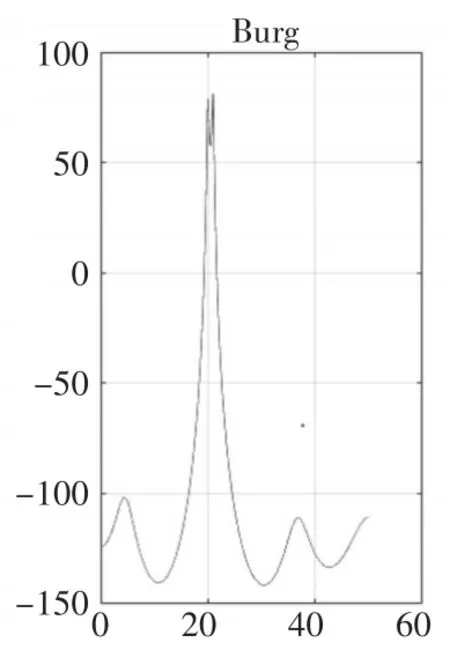
圖7 p=10時(shí)

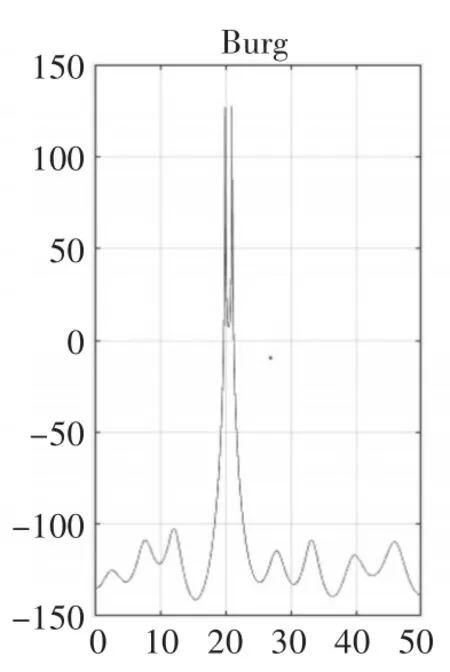
圖8 p=20時(shí)

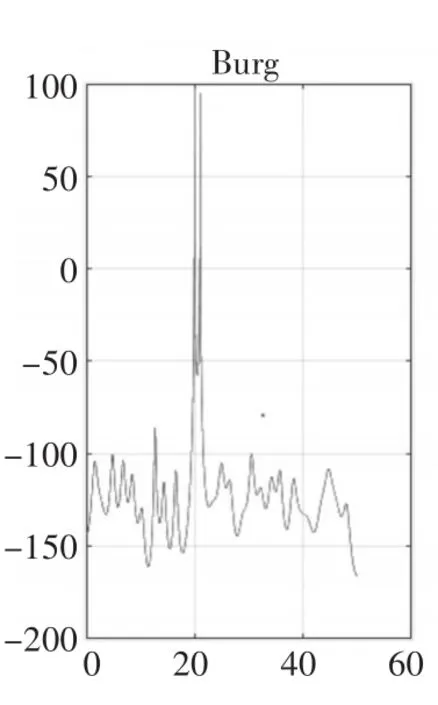
圖9 p=56（N/4）時(shí)

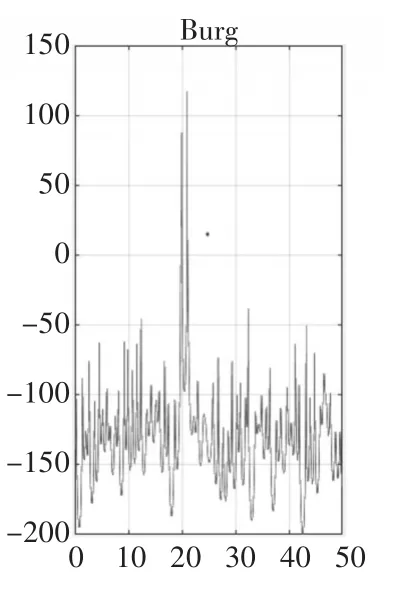
圖10 p=128（N/2）時(shí)

仿真結(jié)果顯示：階次較低時(shí)，Burg法與Levinson法性能相似，如圖1與圖7所示，但是隨著階次的提高，Burg法的譜峰比Levinson法更加尖銳，準(zhǔn)確度更高，如圖10和圖11比圖4和圖5尖銳很多，但是虛假譜峰現(xiàn)象更加嚴(yán)重，譜線更加不穩(wěn)定，毛刺較多，圖11中p=N/2時(shí)出現(xiàn)譜裂現(xiàn)象，嚴(yán)重影響了Burg法的性能。

3.2 在不同的頻率差下，兩種算法譜分辨率的比較

圖11（a）、（b）、（c）的信號是兩個(gè)單頻信號的疊加加上一個(gè)高斯白噪聲（信噪比為10dB）的功率譜估計(jì)圖。x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+（1/20）*randn（size（n））

采樣點(diǎn)數(shù)：256，采樣頻率：100。

圖 11（a）、（b）、（c）分別為頻率差為 3Hz、5Hz、1Hz時(shí)，兩種方法在FPE最佳階次準(zhǔn)則下的AR模型功率譜圖。

分析：

1）圖11（a）所示，在相同的信號情況下，用FPE準(zhǔn)則算出的Levinson最佳階次比Burg算法的低。（不論倆個(gè)信號頻差多少），在最佳階次下，Burg算法的結(jié)果毛刺較多，功率譜的方差較大，而Levinson法的譜線相對平滑。

2）Levinson算法的分辨率比Burg低，在圖（c）中兩個(gè)信號頻率差為1Hz，Levinson已經(jīng)不能分辨。

3）圖11（b）所示，Burg算法有譜裂現(xiàn)象，特別是當(dāng)階次較高時(shí)。所以FPE準(zhǔn)則對于Burg算法預(yù)測的階次偏高，應(yīng)稍微降低階次來減少譜裂，而對Levinson算法來說階次偏低，應(yīng)增加階次來提高分辨率。

3.3 信號頻率差與最佳階次的關(guān)系

圖12（a）、圖12（b）分別是Levinson算法、Burg算法最佳階次隨頻率差的變化圖。

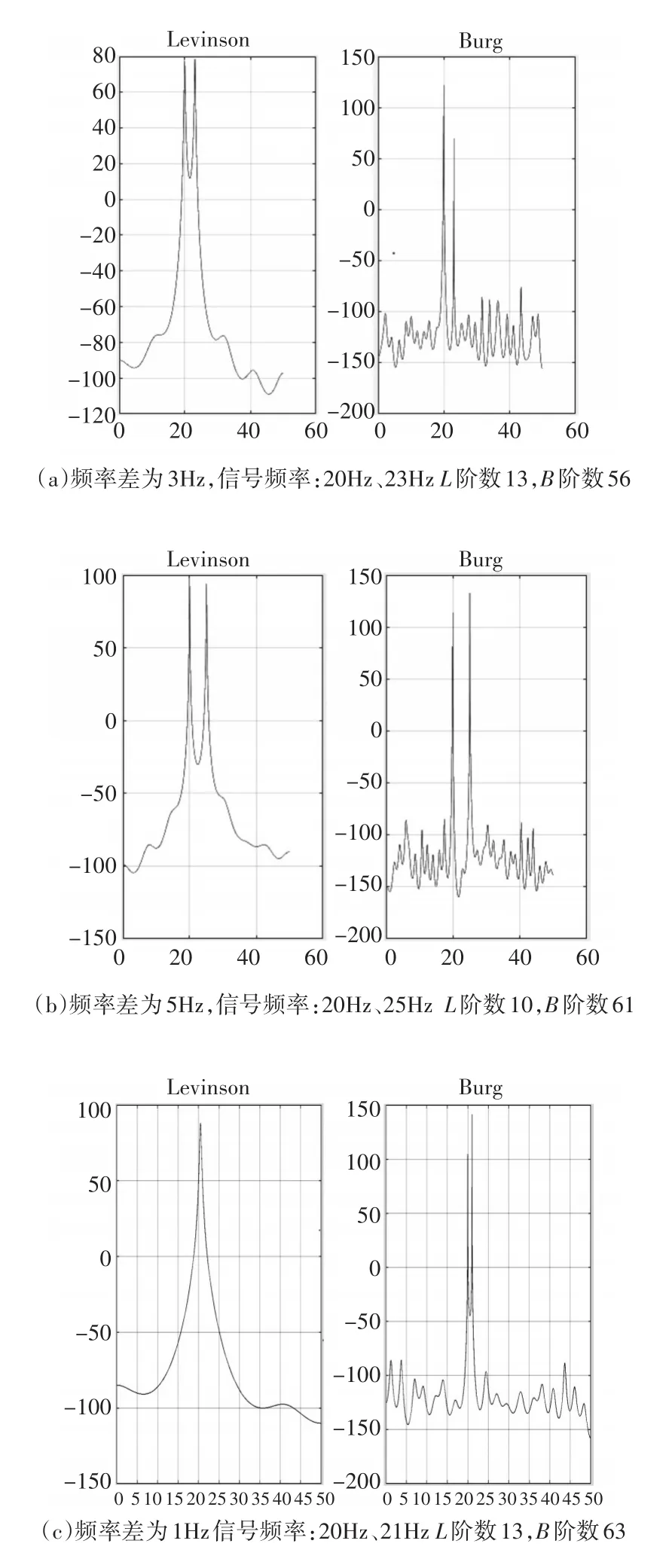
圖11 兩種方法在FPE最佳階次準(zhǔn)則下的AR模型功率譜圖

分析：1）實(shí)驗(yàn)數(shù)據(jù)表明用FPE準(zhǔn)則計(jì)算出的最佳階次確實(shí)隨著頻率差的變換而變換。

2）對于Levinson算法，最佳階次隨頩差的變換曲線呈現(xiàn)單峰性質(zhì)，在3Hz最有出現(xiàn)最大的階次。而對于Burg算法，最佳階次普遍偏高，且最佳階次隨頩差的變換呈現(xiàn)雙峰特征。

3.4 信號頻率差對AR模型預(yù)測誤差的影響

分析：1）Levinson算法的誤差較大，Burg算法的誤差較小，這主要是由于Burg算法FPE最佳階次準(zhǔn)則中階次較高引起的。2）與Levinson相比，Burg法的誤差變化相對較小，預(yù)測精度比較穩(wěn)定。

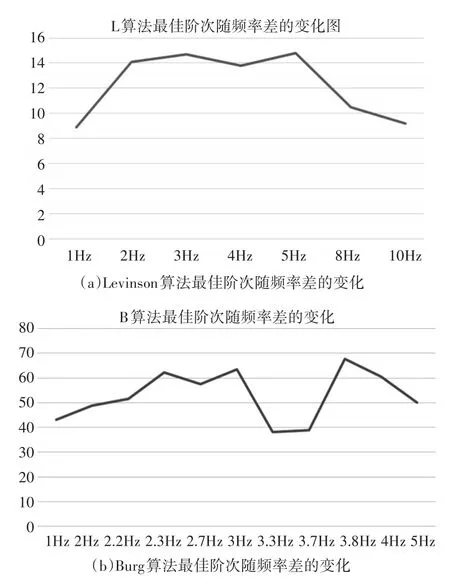
圖12 兩種算法最佳階次隨頻率差的變化圖

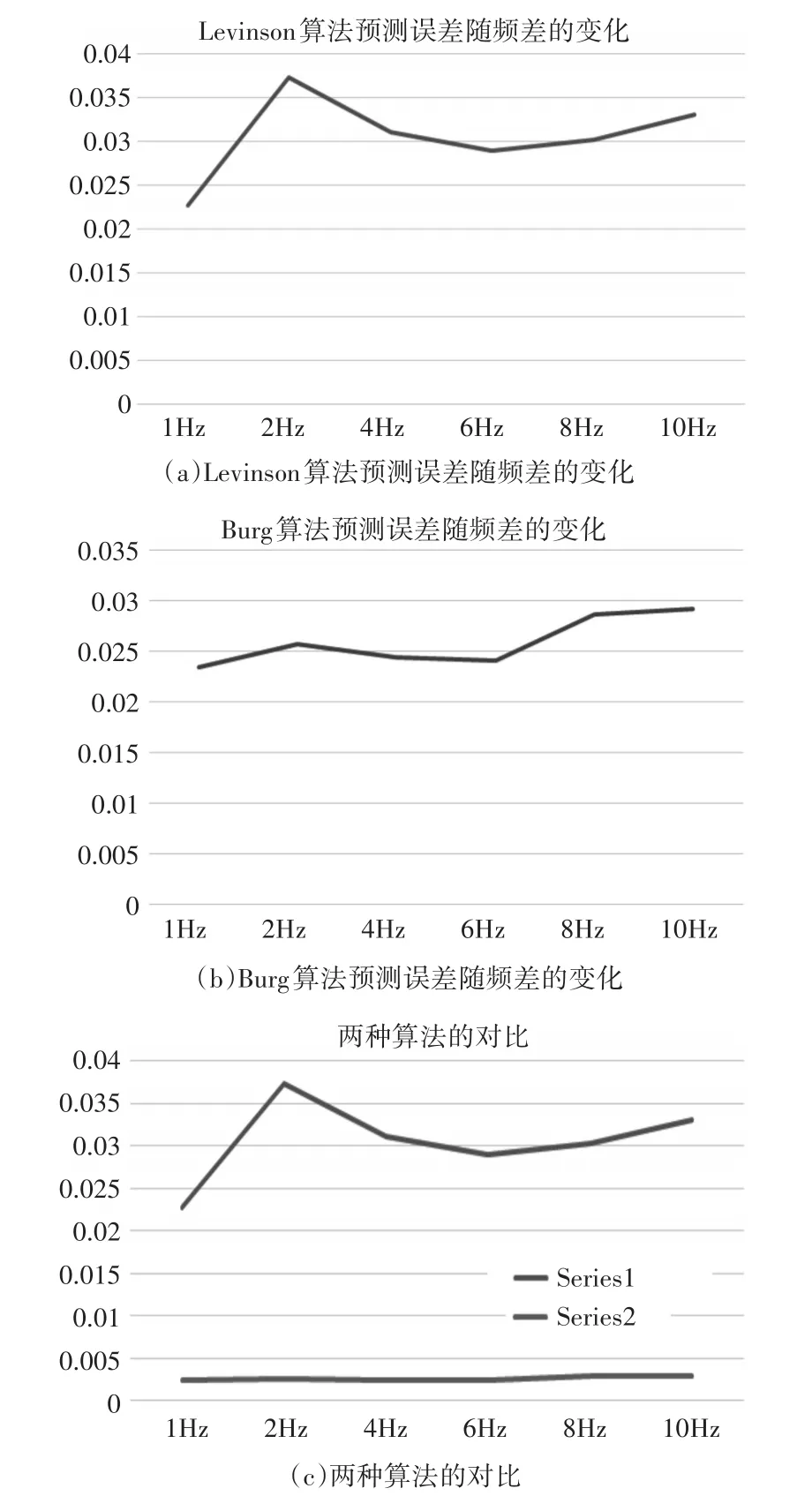
圖13 兩種算法預(yù)測誤差隨頻差的變化圖

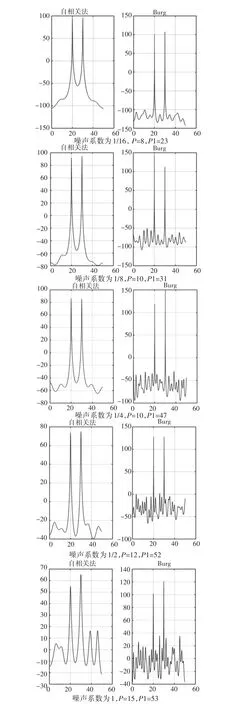
圖14 信噪比變化下兩種方法的性能比較

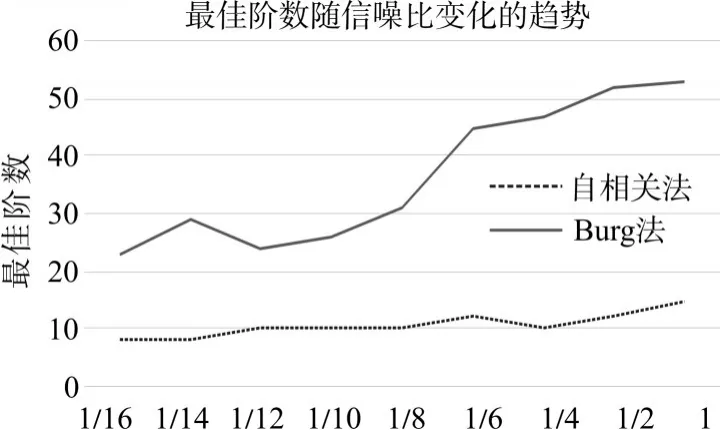
圖15 最佳階次隨信噪比變化的趨勢

4 小信噪比性能分析

本文采用了以下方法進(jìn)行了仿真：x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+m*randn（size（n））

m為噪聲系數(shù)，可知，m越大，信噪比越小。采樣點(diǎn)數(shù)：256，采樣頻率：100，信號頻率：20Hz、30Hz。

4.1 信噪比變化下兩種方法的性能

輸出階數(shù)P，輸出階數(shù)P1（p為自相關(guān)法，p1為Burg法）

由此發(fā)現(xiàn)，在信噪比逐漸減小的過程中，自相關(guān)法的最佳階次變化不大且緩步上升，而Burg法的最佳階次卻有了明顯的增加，并且虛假譜峰現(xiàn)象更加嚴(yán)重，這表明了Burg法在較小的信噪比的情況下性能會下降，而自相關(guān)法卻沒有較為明顯的變化。

4.2 相同階數(shù)下改變噪聲系數(shù)對兩種方法的影響

x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+m*randn（size（n）），m為噪聲系數(shù)，可知，m越大，信噪比越小。采樣點(diǎn)數(shù)：256，采樣頻率：100，信號頻率：20Hz、30Hz。本次選取一個(gè)較大的階數(shù)p=p1=61，改變噪聲系數(shù)，觀測兩種方法預(yù)測的功率譜，見圖16。

由這些圖進(jìn)行比對后發(fā)現(xiàn)，相同的階次情況下，在噪聲系數(shù)較小時(shí)（信噪比較大），Levinson算法分辨率較低，主瓣寬度較大，尖峰處沒有Burg法尖銳，盡管Burg法虛假譜峰現(xiàn)象比Levinson法嚴(yán)重，但總體而言，Levinson法性能相較于Burg法較差。

5 結(jié)語

本文通過Matlab仿真分析，對比研究了Lenvinson（自相關(guān)）算法和Burg算法下的AR模型的譜分辨率，分析了小信噪比情況下的AR模型的性能，主要結(jié)論如下：

1）預(yù)測階次較低時(shí)，Burg法與Levinson法性能相似，但是隨著階次的提高，Burg法的譜峰比Levinson法更加尖銳，準(zhǔn)確度更高，但虛假譜峰現(xiàn)象更加嚴(yán)重。

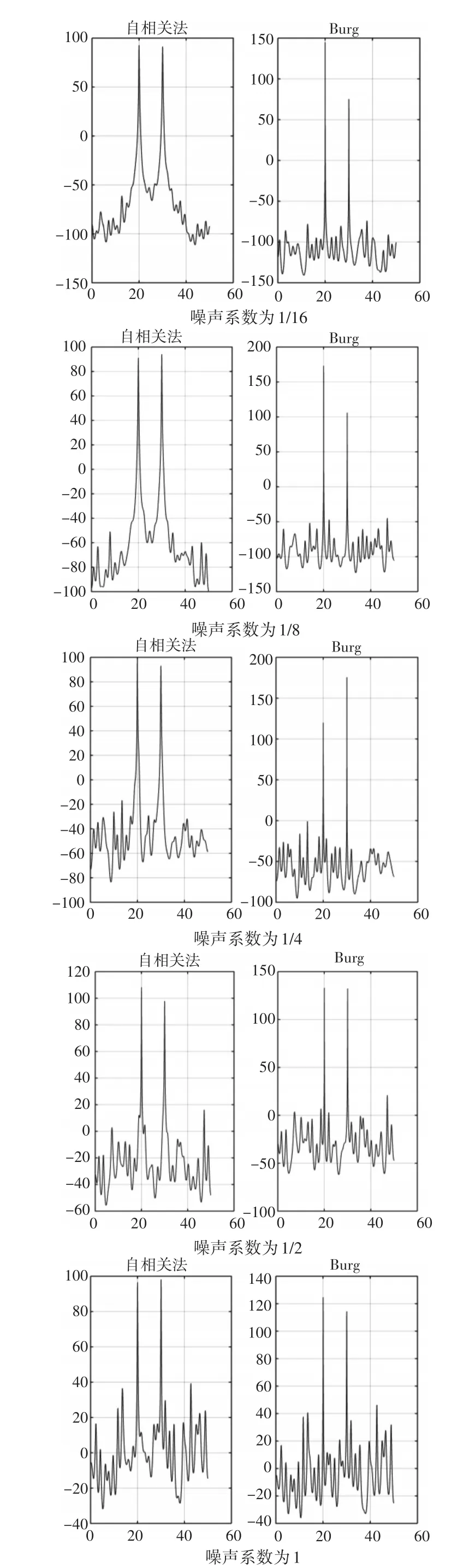
圖16 改變噪聲系數(shù)，Levinson算法和Burg法預(yù)測的功率譜比較

2）在最佳階次下，Burg算法功率譜的方差較大，而Levinson法的譜線相對平滑。FPE準(zhǔn)則對于Burg算法預(yù)測的階次偏高，應(yīng)稍微降低階次來減少譜裂，而對Levinson算法來說階次偏低，應(yīng)增加階次來提高分辨率。

3）與Levinson相比，Burg法的預(yù)測誤差隨頻差的變化相對較小，預(yù)測精度比較穩(wěn)定。

4）Burg法在較小的信噪比的情況下性能會下降，而自相關(guān)法卻沒有較為明顯的變化。

5）相同的階次情況下，在噪聲系數(shù)較小時(shí)（信噪比較大），Levinson算法分辨率較低，主瓣寬度較大，尖峰處沒有Burg法尖銳，盡管Burg法虛假譜峰現(xiàn)象比Levinson法嚴(yán)重，但總體而言，Levinson法性能相較于Burg法較差。