兩種卡爾曼濾波辨識高速旋轉彈丸阻力系數的對比

鄭宇程，易文俊，余春華，管 軍

(1.南京理工大學 瞬態物理國家重點實驗室， 南京 210094； 2.南京理工大學 理學院， 南京 210094)

火炮在現代戰爭中具有重要的使命，在對敵火力壓制過程中能夠起到關鍵性作用。獲取傳統高速旋轉穩定彈丸準確的氣動參數，對于提高火炮射表精度、減小落點散布、增強打擊精度具有重要的意義。目前，國內外獲取彈丸氣動參數的方法主要有三種[1]：第一種是理論計算，第二種是風洞吹風，第三種是利用彈丸的自由飛行數據對彈丸的氣動參數進行離線辨識。理論計算法雖然簡單，但由于模型中的未建模因素和不確定因素導致計算結果存在誤差。風洞吹風法作用于彈丸模型，結果較為準確但成本較高，不能精準模擬高速旋轉狀態。利用彈丸自由飛行數據辨識彈丸的氣動參數，不僅符合實際情況，還能根據辨識結果，及時對彈丸運動狀態進行調整，從而提高炮彈的打擊精度。

用于參數辨識的方法通常有遞推最小二乘法、遞推極大似然法、卡爾曼(kalman)濾波法等[2-5]。近年來，許多學者對此進行了研究。史繼剛[2]基于粒子群初值選取的牛頓迭代優化算法辨識彈丸的零升阻力系數，該方法基于最大似然準則，相比于卡爾曼濾波法實現更加困難；管軍等[3]提出一種新的自適應混沌變異粒子群算法求解該準則下的氣動參數最優解，得到彈丸的氣動參數，但是在工程上難以實現；Rogers等[4]提出了一種基于證據理論的參數估計方法，偏于理論計算；史金光等[6]利用擴展卡爾曼濾波法對彈道修正彈的阻力和升力符合系數進行了辨識，并且由此對后續彈道進行修正，然而該方法技術要求較高，難以在實際應用中實現；楊靖等[7]利用改進的混雜擴展卡爾曼濾波法對彈丸的阻力系數進行辨識，其對EKF的改進不大。

相比于最小二乘法和極大似然法，卡爾曼濾波法應用最為廣泛。在處理非線性問題上，擴展性卡爾曼濾波(EKF)和無跡卡爾曼濾波(UKF)已經成功地應用于各種參數辨識問題[8-11]。本文主要利用擴展卡爾曼濾波和無跡卡爾曼濾波對彈丸的阻力系數進行辨識，并進行了對比研究。為了進行氣動參數的辨識，本文將未知的氣動參數看成系統的狀態量，分別用EKF方法和UKF方法對氣動參數進行辨識。為了檢驗實驗的正確性，又分為氣動參數不變和氣動參數變化兩種情況進行研究。

1 彈道模型

參數辨識的本質問題就是如何通過輸出數據準確辨識相關輸入參數或系統參數。如何選取系統的模型是重要的步驟之一。

阻力系數是傳統無控旋轉彈丸所有氣動參數中最重要的氣動參數之一，其直接影響了彈丸的射程和落點散布。本文的主要研究內容是彈丸阻力系數辨識，雖然外彈道學中的彈道模型多種多樣，但2D彈道模型已經能夠描述阻力系數對彈道性能的絕大部分影響。且2D彈道模型簡單、便捷，能夠直接揭示阻力系數和彈道參數之間的關系。因此，本文選用2D彈道模型作為系統的模型。

2D彈道模型[12]的方程為

(1)

其中，ρ為當前高度的大氣密度，S為參考面積，m為彈體質量。

2 卡爾曼濾波原理

2.1 擴展卡爾曼濾波算法

卡爾曼濾波法最初只用于離散線性系統，后來經過改進，產生了許多種不同的方法。擴展性卡爾曼濾波(EKF)和無跡卡爾曼濾波(UKF)是應用得比較廣泛的兩種方法。EKF方法在線性化處理的過程中對原系統進行泰勒展開，略去了二階以及二階以上的高階項，只保留了線性項。

擴展卡爾曼濾波的基本原理為：

1) 狀態一步預測方程

(2)

2) 求一步預測均方誤差

(3)

式中：Qk-1是系統噪聲的協方差矩陣，Γk-1是系統噪聲驅動陣，Φk,k-1為一步轉移矩陣，計算式如下：

Φk,k-1=I+A·Δt

(4)

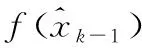
3) 求濾波增益矩陣

(5)

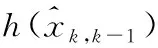
4) 估計均方誤差

Pk=[I-KkHk]Pk,k-1

(6)

5) 得到最新一步的狀態估計

(7)

式中，zk為k時刻的觀測向量。

2.2 無跡卡爾曼濾波算法

由于EKF是一種非線性估計問題的線性化方法，其線性化過程會產生一定的誤差，且其需要進行復雜的雅克比矩陣求解；而UKF通過UT變換，直接對非線性問題進行處理，不需進行復雜的雅克比矩陣求解，且其精度可以達到二階泰勒展開的精度。因此，本文同樣使用UKF對阻力系數進行辨識，并同EKF進行比較研究，其基本計算步驟為：

1) 初始化濾波參數

(8)

式中：n為增廣狀態向量的維數；α是很小的一個正數，其取值范圍為10-4～1。本文取為0.01；κ的取值為3-n；β的值與x的分布形式有關，對于正態分布的情況，β取2最優。

2) 計算k-1時刻的sigma樣本點

(9)

3) 計算k時刻的一步預測值

(10)

4) 計算k時刻的一步預測樣本點

(11)

5) 計算P(XZ)k,k-1和P(ZZ)k,k-1

(12)

6) 更新濾波值

(13)

3 基于卡爾曼濾波的阻力系數辨識

由于待辨識參數是阻力系數CD，本文通過增廣的方法將其添加到式(1)，以建立包含待辨識參數的狀態方程。

利用系數凍結法，設在小區間內彈丸的阻力系數是常數，因此有下式成立：

(14)

則增廣狀態變量x為

x=[u,θ,x,y,CD]T

(15)

增廣之后的狀態方程可寫為

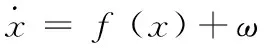
(16)

ω為系統噪聲向量。

通常情況下，彈道跟蹤雷達只能得到彈丸的速度和位置信息，因此量測向量取為

z=[u,x,y]T

(17)

量測方程為

z=h(x)+v

(18)

v為觀測噪聲向量。

4 數值仿真

彈丸的物理參數為：彈重45.5 kg；彈徑0.155 m；彈長0.909 m。氣象條件為標準氣象條件[13]。射擊初始值為：初速930 m/s，射角45°。

狀態初值為

x0=[930,45°,0,0,CD]Τ

(19)

初始狀態誤差協方差矩陣為

(20)

系統噪聲的協方差矩陣為

(21)

量測噪聲的協方差矩陣為

(22)

算例1

假設CD為常數，其真實值為0.35。用CD為0.35計算出來的理論值(速度，位置坐標)加上高斯白噪聲v來模擬觀測值。對于CD為常數的情況，用EKF和UKF辨識結果如圖1～圖2所示。從圖1和圖2可以看出，兩種方法辨識的CD最終都收斂在0.35，但UKF具有更快的收斂速度。

算例2

實際情況中，阻力系數CD是馬赫數的函數，本算例所采用的數值如表1所示。

根據變化的CD計算出的理論值，加上高斯白噪聲v的值，將其用來模擬觀測值。將EKF與UKF辨識的馬赫數與真實的馬赫數之差畫成曲線在一起對比，如圖3所示。

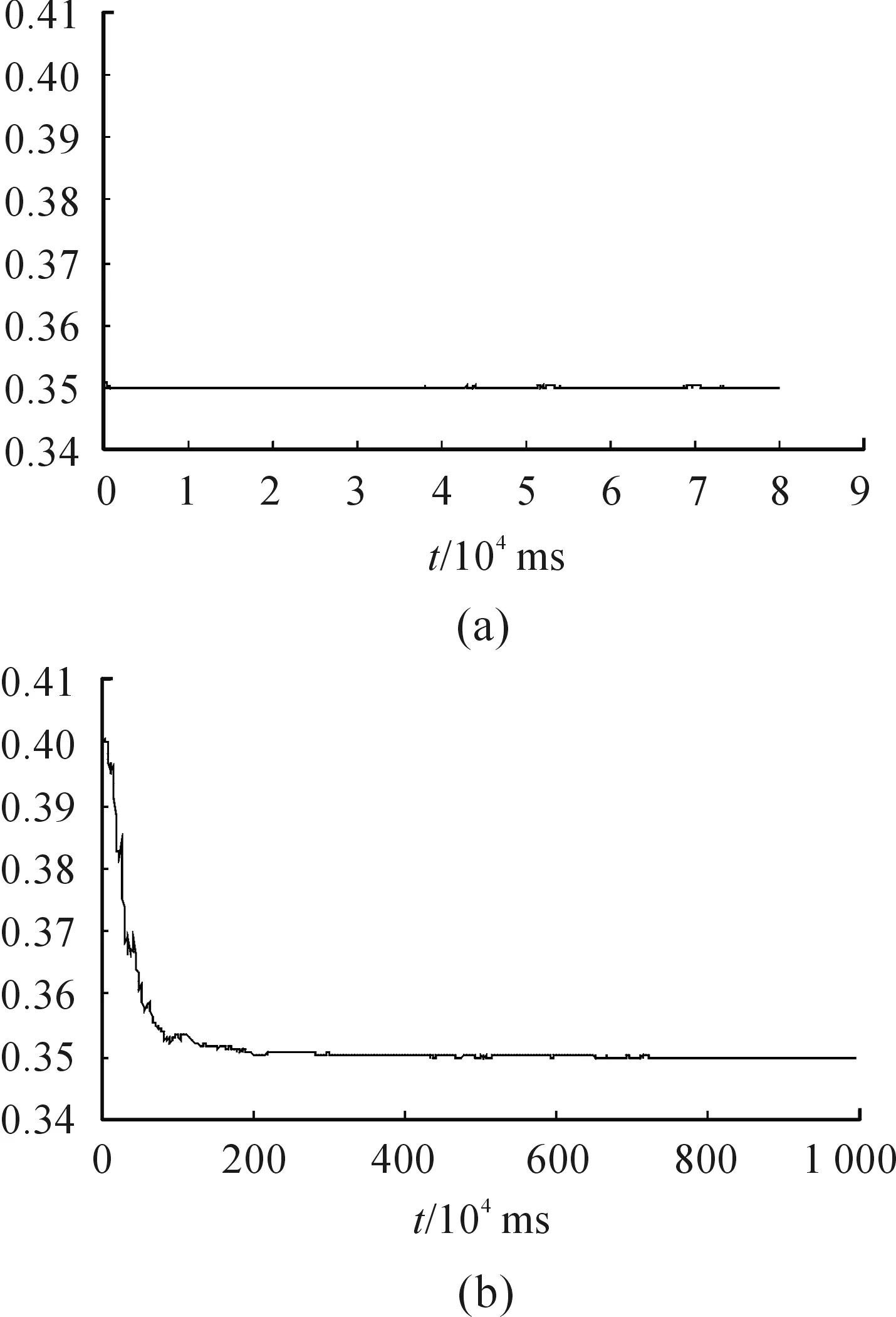
圖1 EKF辨識CD不變

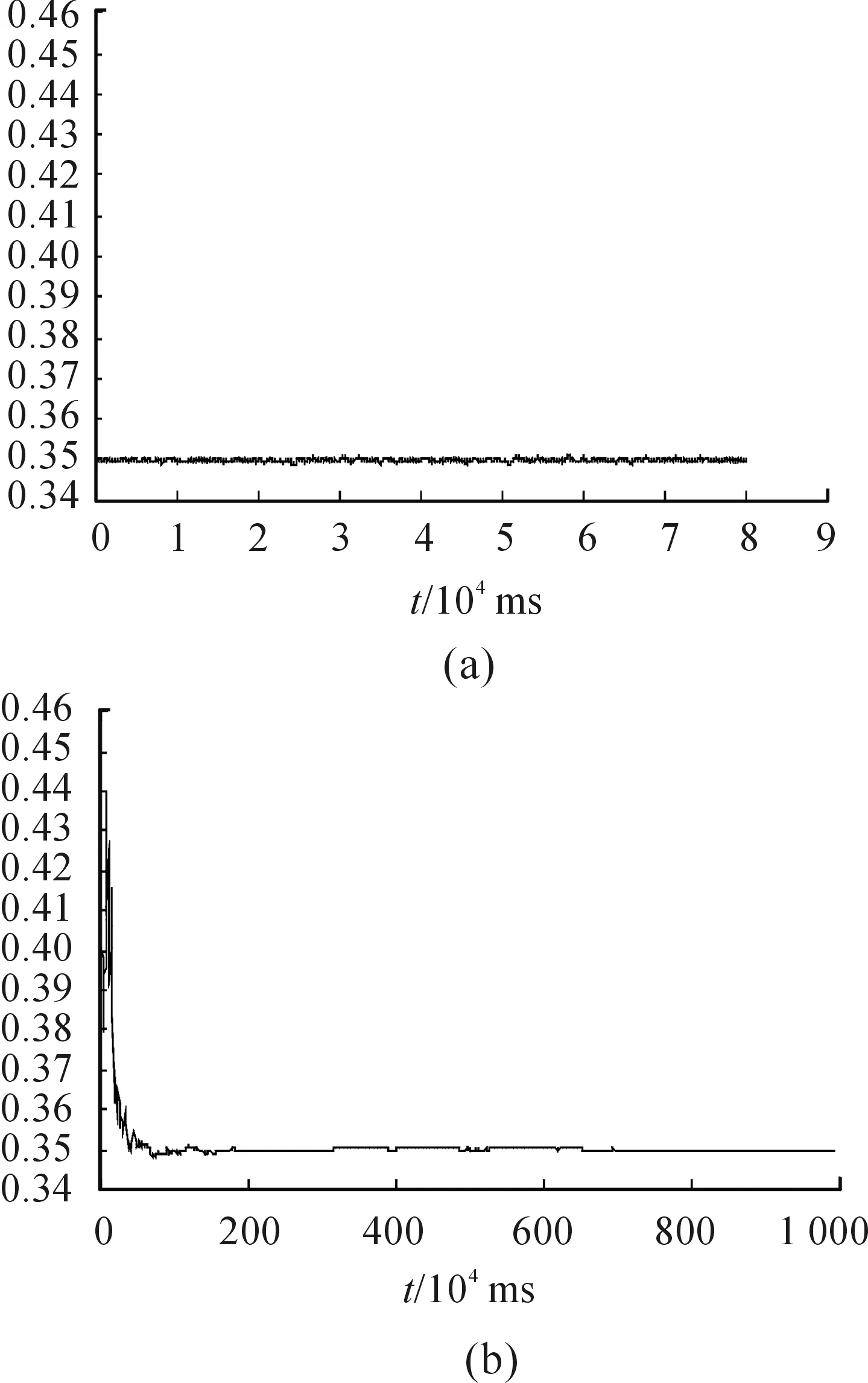
圖2 UKF辨識CD不變

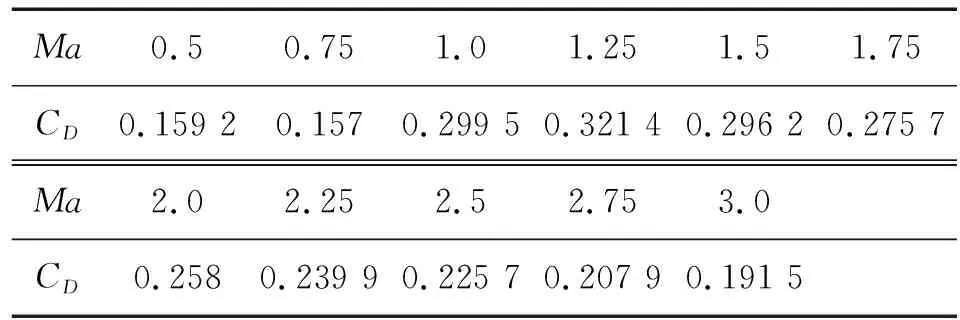
Ma0.50.751.01.251.51.75CD0.159 20.1570.299 50.321 40.296 20.275 7Ma2.02.252.52.753.0CD0.2580.239 90.225 70.207 90.191 5

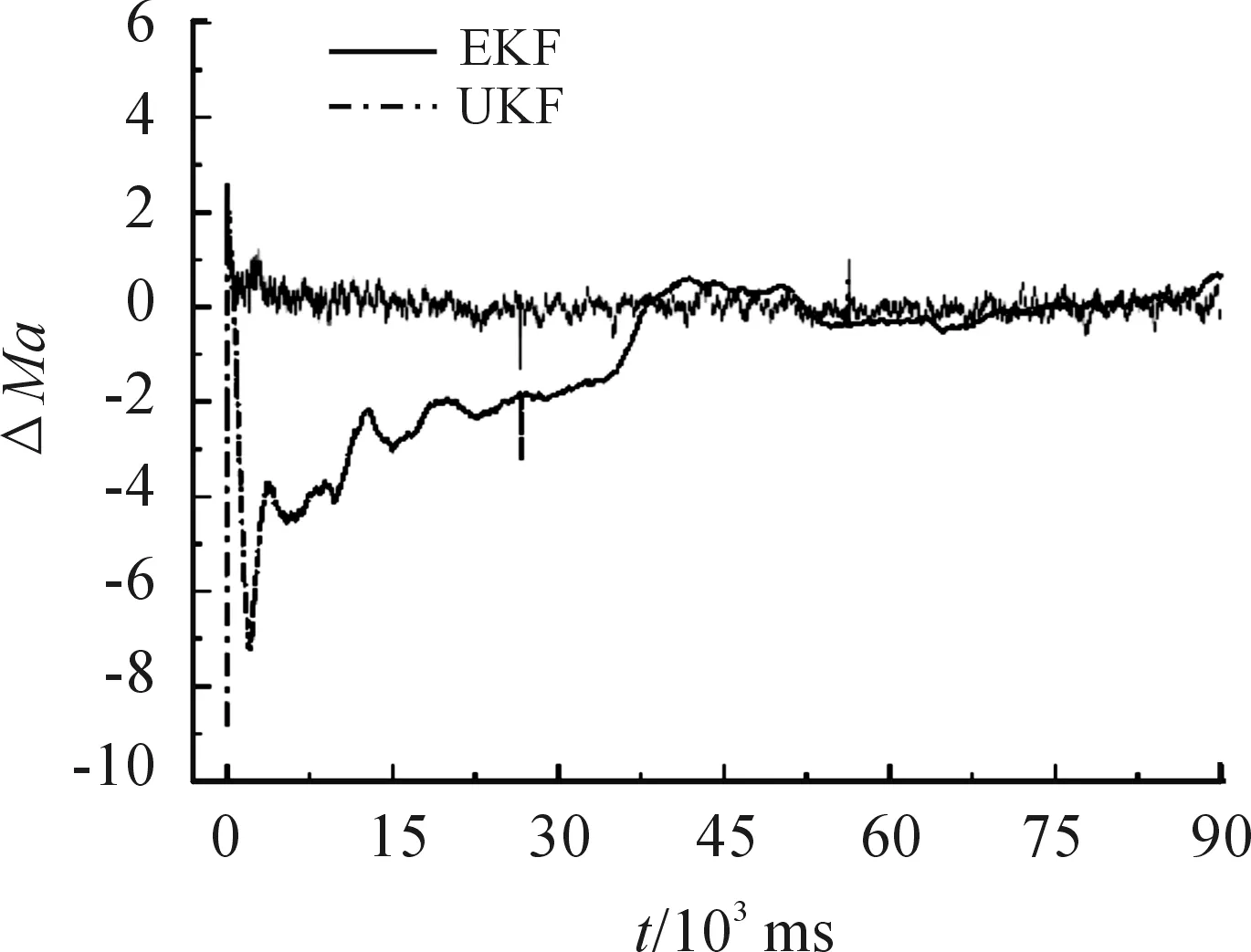
圖3 馬赫數辨識誤差曲線

圖3不但表示了CD隨馬赫數變化的情況，而且可看出UKF辨識的馬赫數誤差較小，EKF辨識的馬赫數誤差較大。但是最大的誤差不超過10-3，為原馬赫數的0.05%，因此認為兩種方法辨識的馬赫數是準確的。CD雖然是馬赫數的函數，但是為了便于比較研究，將真實CD曲線、EKF辨識CD曲線和UKF辨識CD曲線對比，如圖4所示。

從圖4可以看出，前后兩端三者差別不大，現在選取中間20～50 s的時間段，參見圖5。

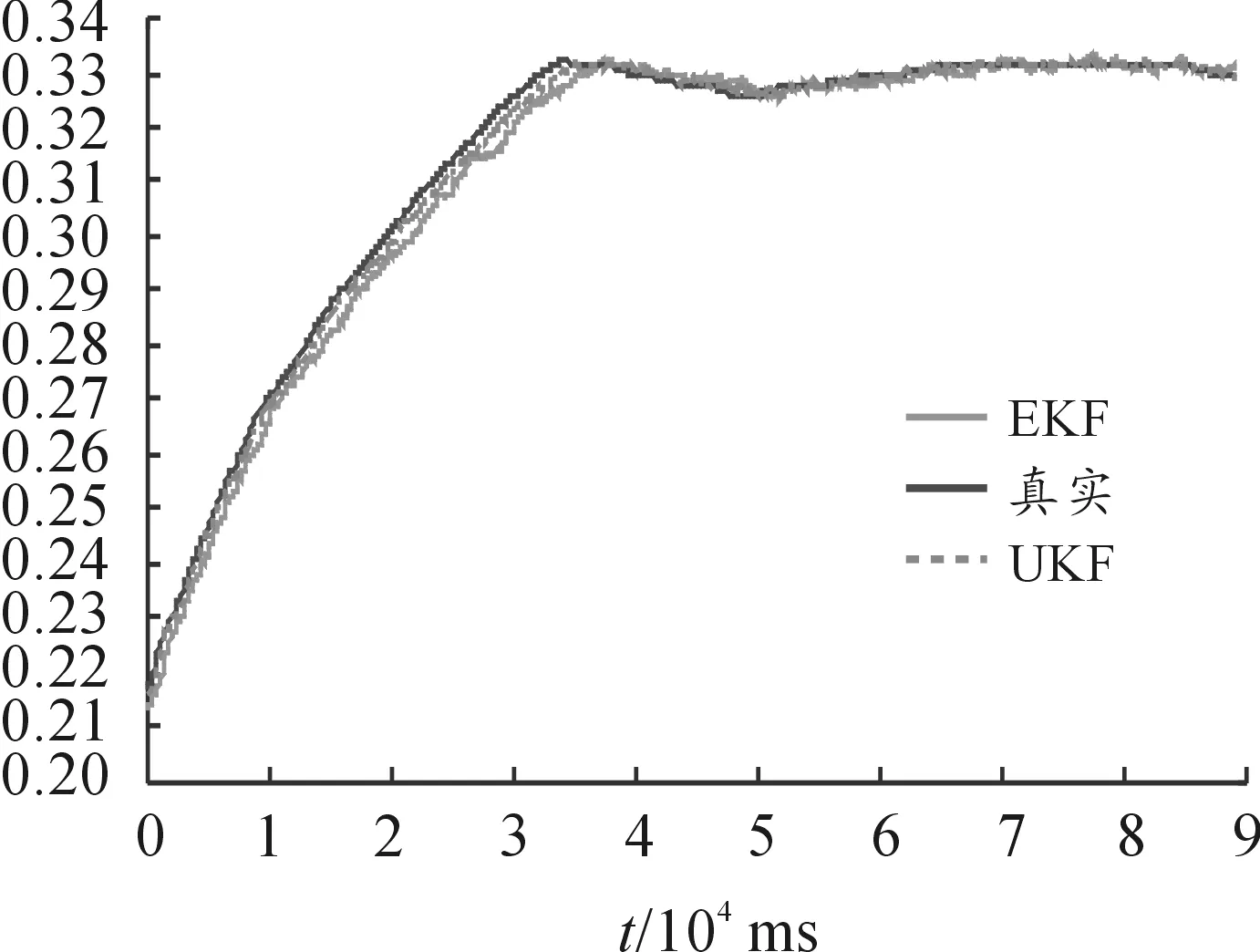
圖4 EKF與UKF辨識結果對比(1)

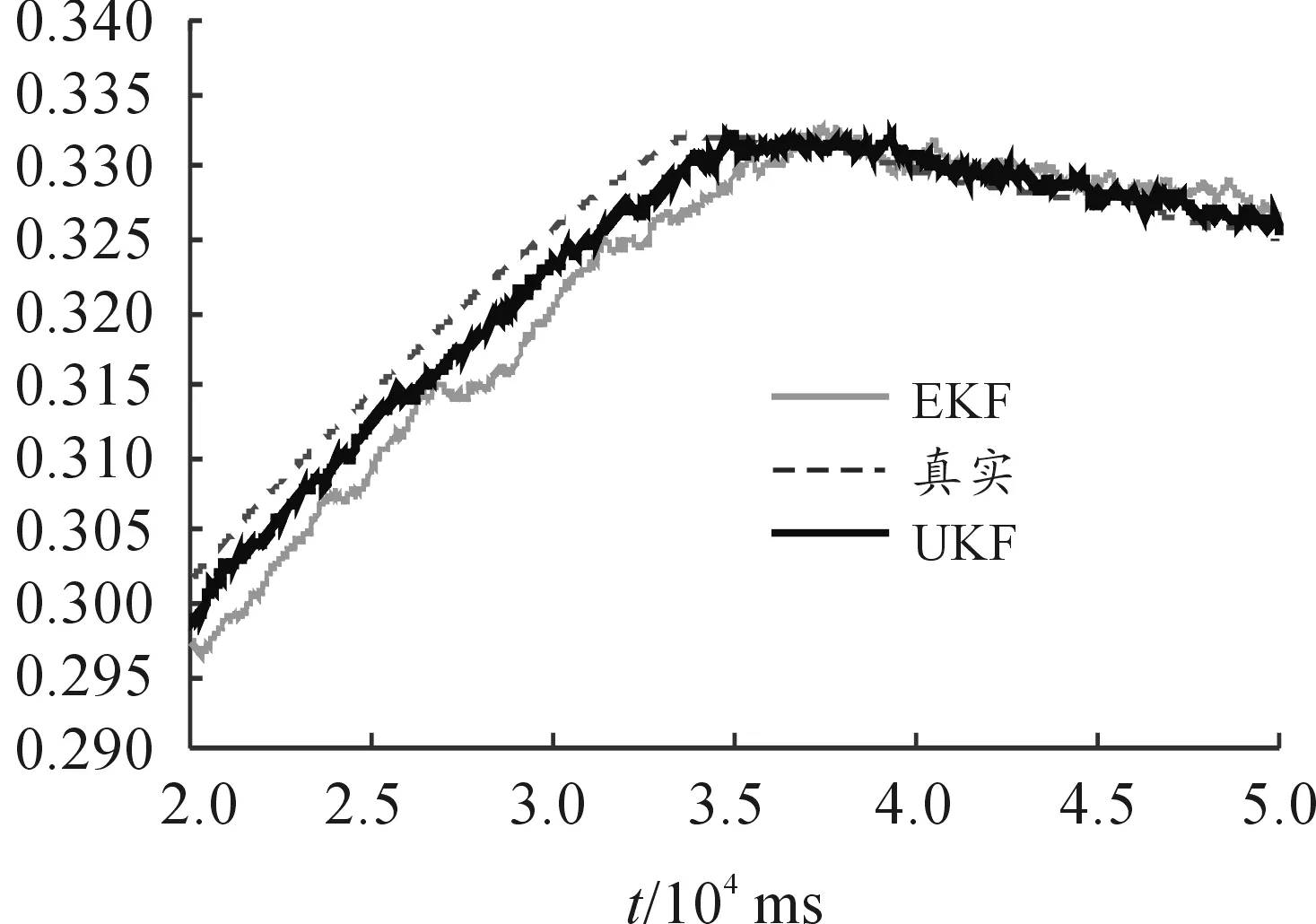
圖5 EKF與UKF辨識結果對比(2)

圖5中，從上至下分別是真實CD曲線、UKF辨識曲線和EKF辨識曲線。經過比較，UKF辨識曲線的精度較EKF高，兩者的差距在0.002 5左右。UKF辨識的誤差為0.8%，EKF辨識的誤差為1.6%。由此可見，參數辨識的結果具有可行性。

5 結論

1)CD不變的情況下，EKF方法與UKF方法都能快速收斂到真值，且UKF具有較快的收斂速度。

2)CD隨馬赫數變化的情況下，EKF方法與UKF方法都能有效辨識出阻力系數，且UKF較EKF具有更高的辨識精度。