長桿彈低速撞擊剛性靶板過程中的過載特性研究

王耀羚，盧玉斌

(西南科技大學 制造過程測試技術教育部重點實驗室， 四川 綿陽 621010)

侵徹是一個復雜過程，侵徹的研究由于其學科的特殊性，成為各國學者的研究熱點之一[1]。侵徹過程是一個動態過程，其動態復雜性決定了侵徹過程中含有許多瞬變成分的非平穩信號，必須基于加速度計獲取真實可靠的彈體侵徹過載，然后對所測過載數據進行系統分析，進而得到彈體過載變化規律，為精確有效計算出侵徹深度提供可靠的數據支持[2]。在侵徹研究中，根據侵徹速度不同，可分為高速、中速和低速侵徹，目前國內外學者研究的重點是高速和中速彈體的侵徹實驗，而對于低速侵徹的研究較少。對于高速侵徹，國內外許多學者實驗發現，加速度傳感器采集的過載信號經過一次與二次積分后，得到的侵徹速度與侵徹深度和實際測量數據有較大的差值[3-4]。影響侵徹的因素許多，文獻[5]發現長桿彈彈頭形狀對侵徹深度有較大影響。為了簡化問題，分析導致加速度積分值與實際值偏差的原因，本研究以平頭長桿彈低速撞擊剛性墻為對象，研究不同速度下的加速度變化特性，對比分析加速度曲線的積分值與速度和位移，為中、高速侵徹時準確測量過載提出解決措施。

1 數值模擬模型

彈體垂直撞擊剛性墻，長桿彈的長徑比(L/d)為10，L=500 mm，d=50 mm。彈體的材料參數如表1所示。

表1 長桿彈材料參數

數值模擬主要研究在低速撞擊情況下，不同加載速度時彈體的碰撞端和非碰撞端的加速度變化以及彈體的平均加速度變化，加載速度在3～10 m/s范圍內。計算結果表明，在這幾種極低的加載速度下，彈體均不會發生塑形形變，彈體變形在彈性階段。

基于自由落體運動，將長桿彈從設定的高度釋放，讓其垂直自由下落并和靶板發生碰撞，從而產生不同的加載速度。在ABAQUS仿真過程中，將長桿彈和靶板定義為直接無間隙接觸，如圖1所示。

圖1 長桿彈和靶板無間隙接觸

本研究在數值模擬中采用六面體單元，設置單元類型時選擇C3D8R實體單元進行模擬，在網格控制中選擇中軸線算法(Medial axis)劃分網格，這種算法能提高處理回轉體模型的效率和精確度[6]。劃分網格后總共有44 202個單元，48 640個節點，如圖2所示。

圖2 長桿彈的網格劃分

2 理論加速度峰值計算

2.1 彈性應力波分析

通過應力波分析，長桿彈低速撞擊剛性靶板的沖擊不大，桿處于彈性變形下，應力波是一維線性彈性波。對線性彈性波而言，波速恒定，在均勻介質中傳播其波形恒定不變。

根據牛頓第二定律，得到：

(1)

引入σ=P/A0，化簡得到：

(2)

引入常數C，可得出：

(3)

桿處于彈性形變時，應力和應變滿足Hooke定律，其本構關系為：

σ=Eε

(4)

式中：E為楊氏模量，由此得出常數C僅由材料本身屬性ρ0和E所決定。

(5)

由此可知桿中彈性應力波波速與外界條件無關。代入材料參數得到彈性應力波的波速C0=5 190 m/s。

彈性波在有限長度桿中傳播，波長λ近似為長桿L，有λ=L=0.5 m，撞擊產生的應力波在桿中來回振蕩，由此得到波形脈寬的表達式：

(6)

代入數據計算，得出T=96 μs。

2.2 沖擊脈沖理論分析

設長桿彈自由下落的高度為h1，根據牛頓第二定律可得，彈體與靶板碰撞瞬間其速度為：

(7)

碰撞產生的反作用力使長桿彈反彈，假設反彈高度為h2，則碰撞后反彈的速度為：

(8)

若將上述公式作為邊界條件，則碰撞過程中長桿彈的速度變化可以表示為：

(9)

其中T為響應波形的脈寬。

將式(3)進行一次微分運算，得到碰撞過程中長桿彈的加速度變化，表示為：

(10)

由此可以得到碰撞過程中的加速度峰值為：

(11)

式(11)是計算碰撞過程中加速度峰值的基本公式[7]。 給定3 m/s、5 m/s、7 m/s、8 m/s、9 m/s和10 m/s 6種不同的初速度。由于長桿彈以這6種初速度垂直碰撞時，其反彈高度較低，將整個過程簡化，h2賦值為0，并設定波形脈寬T=96 μs[8]。則碰撞過程中加速度峰值的公式可以簡化為：

3 數值模擬結果

3.1 頻率分析

采樣頻率f，也稱為采樣率，定義了從連續信號中提取并組成離散信號的采樣個數，它用赫茲(Hz)表示。在動態分析中，離散信號是由連續信號采樣得到的信號。選擇合適的采樣頻率既能保證信號精確度，也能控制數值模擬計算時間。

本文數值模擬選取f=2 MHz 、1.5 MHz和1 MHz三個不同頻率作為分析參數，對比采用不同頻率時信號的精確度。研究發現采樣頻率和初速度無關，因此選取v=3 m/s時不同頻率下的平均加速度進行對比，如圖3所示。

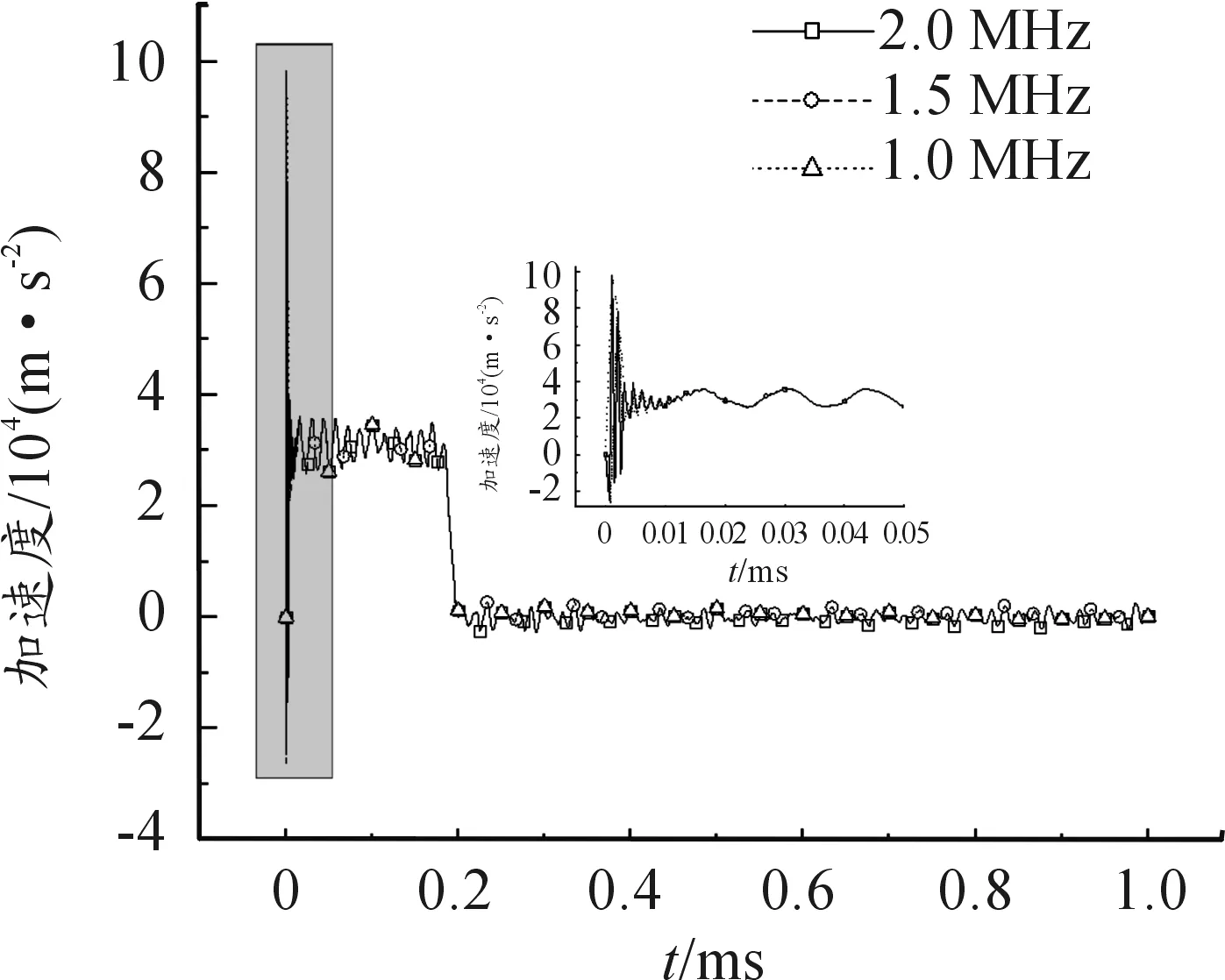
圖3 不同頻率下3 m/s時的平均加速度

從圖3可以看出，不同頻率的平均加速度曲線差別不大，在0.05 ms范圍內，不同頻率下的信號不同。采樣頻率高時獲得的數據更精確，當f=1 MHz時只存在一個波峰；f=1.5 MHz時，波峰波谷各有兩個；當f=2 MHz時，波峰波谷各有3個。說明采樣頻率取2 MHz時比其他兩個頻率能采集到更完整的數據信號。數值模擬計算時間和計算規模受計算機運算能力影響，因此保證數據的精確和降低計算時間選擇2 MHz作為采樣頻率。

3.2 平均加速度分析

靶板為剛體，僅研究平頭長桿彈碰撞時彈體的加速度變化情況。基于數值模擬獲得了上述6種不同初速度加載時的彈體平均加速度峰值。圖4中A1是數值模擬中長桿彈撞擊剛性靶板的平均加速度峰值，A是理論加速度峰值。模擬加速度峰值和理論值有相同的變化趨勢，均隨著侵徹速度的增加而增加。對比發現理論加速度峰值和模擬加速 度峰值有22.5%的偏差。這可能是依據理論公式計算時，把h2取為0，實際上數值模擬時彈體發生了反彈，并且反彈高度會隨著初速度的增大而增大。模擬值和理論值在相同數量級，誤差在許可范圍內，因此本文數值模擬的準確性是可接受的[9]。

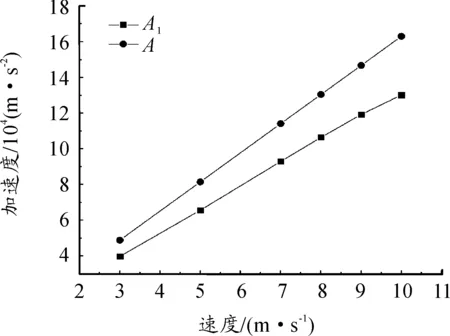
圖4 理論加速度峰值A和模擬加速度峰值A1的比較

當加載速度為3 m/s時，長桿彈的平均加速度曲線如圖5所示。從圖5中可以觀察到，加速度在30 000 m/s2處振蕩。在t=0.196 ms時，長桿彈開始反彈，脫離靶板之后由牛頓第二定律可知，隨著彈體離靶，長桿彈不受靶板的反作用力作用， 然而由于彈體離靶后，還有應力波在彈體中來回傳播，所以加速度在零附近振蕩。對比速度差為2 m/s(3 m/s、5 m/s、7 m/s、9 m/s)撞擊靶板的數據，發現相鄰兩速度的加速度峰值最大相差26 000 m/s2，增長率隨著速度的增大而減小，從66.7%降低到28%，如圖6所示。對比速度差為 1 m/s(7 m/s、8 m/s、9 m/s、10 m/s)撞擊靶板的數據，發現相鄰兩速度的加速度峰值最大相差13 000 m/s2，增長率同樣隨著速度的增大而減小，從14.5%減小到9.1%，如圖7所示。

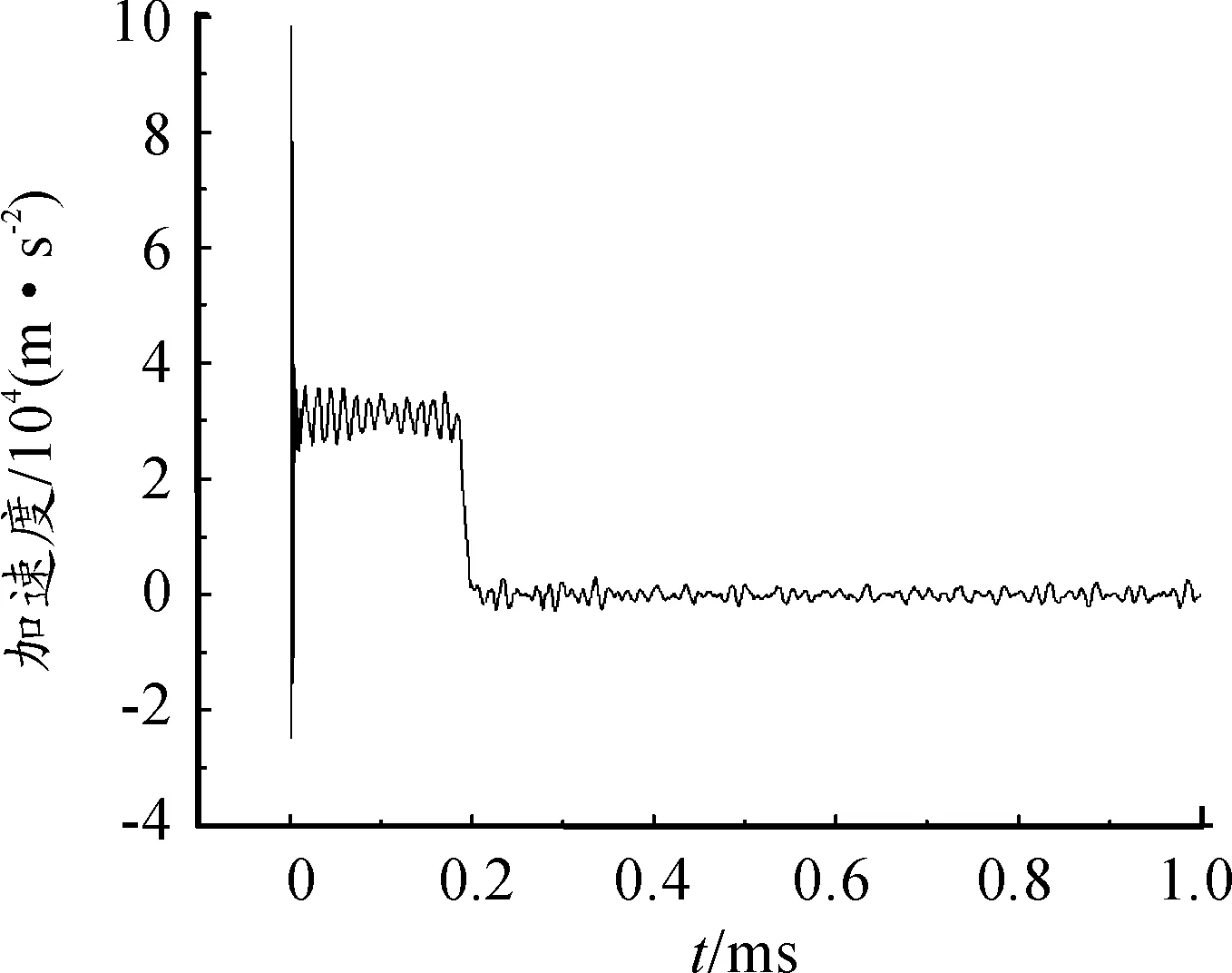
圖5 速度為3 m/s時的平均加速度

分析數據可以發現，加速度波動在一個水平線上，當v=3 m/s時，加速度值在30 000 m/s2處波動；v=5 m/s時，加速度值在50 000 m/s2處波動；當v=7 m/s時，加速度值在 70 000 m/s2處波動；以此類推，當v=8、9、10 m/s時，加速度值在80 000 m/s2、90 000 m/s2、100 000 m/s2處波動。由此可見長桿彈低速撞擊剛性靶板，在彈體材料的彈性階段，彈體平均加速度a滿足：

a=105v

(13)

式中v為加載初速度。

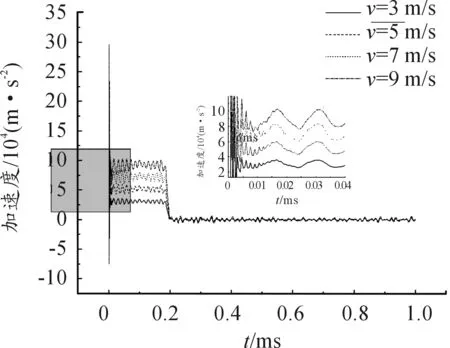
圖6 速度差為2 m/s的平均加速度

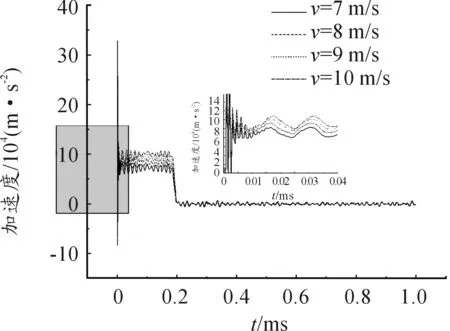
圖7 速度差為1 m/s的平均加速度

3.3 節點加速度分析

本文數值模擬模型中彈體撞擊端中心節點為N28，非撞擊端中心節點為N48364。

對比兩端中心節點的加速度峰值，結論是加載速度越大，撞擊端與非撞擊端加速度的比值λ越大。當v=3 m/s時，比值λ為7.7；當v為10 m/s時，比值λ為15。不同加載速度下，λ的變化曲線如圖8所示。

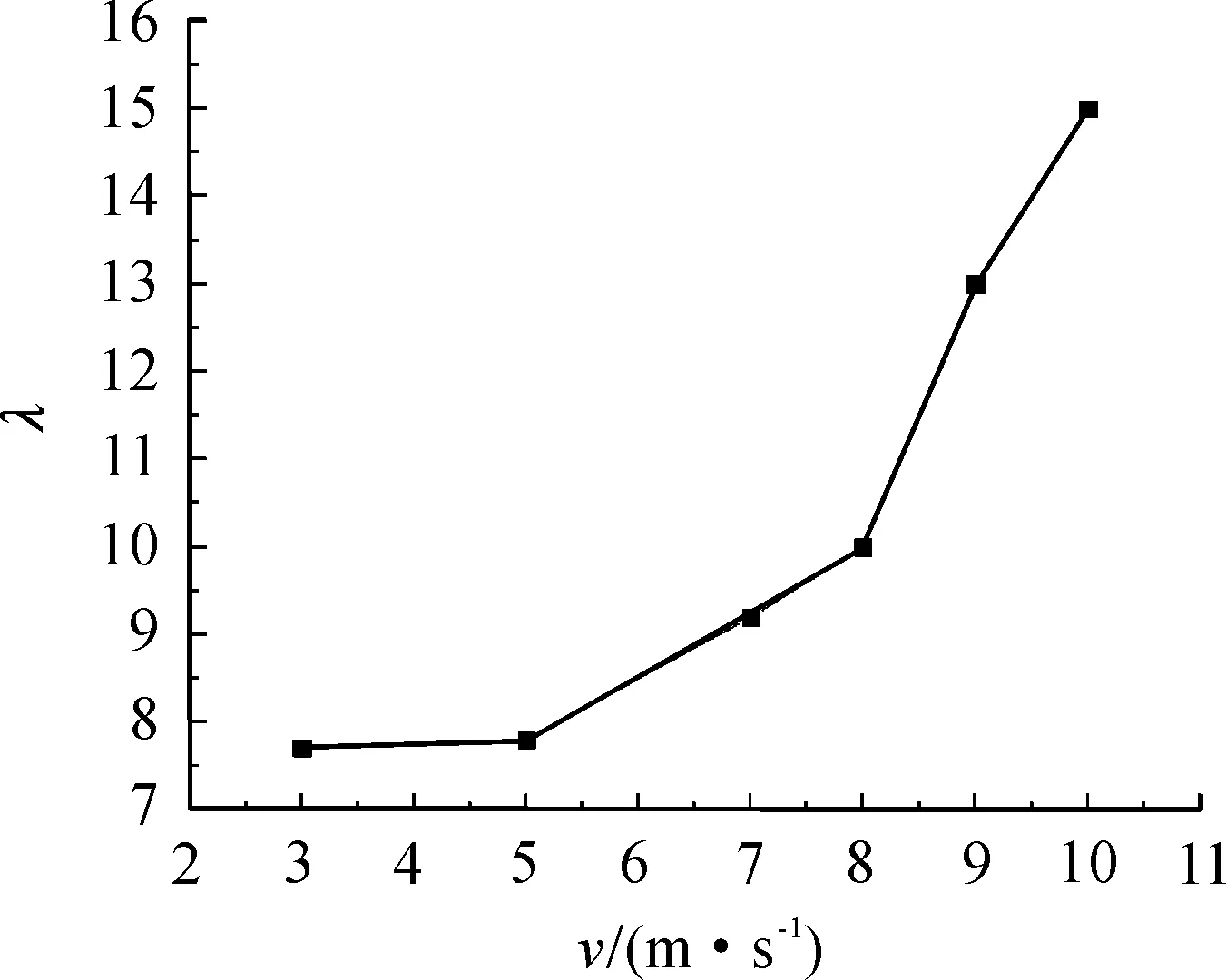
圖8 加速度峰值比

從圖8可以看出，低速撞擊下，撞擊端加速度至少是非撞擊端的7.7倍，隨著加載速度的遞增，λ值迅速增大，這與文獻[10]結果一致。

中心節點N28處加速度一次積分后的速度曲線和撞擊速度曲線對比如圖9所示，圖10所示為加速度二次積分后的位移和靶板形變的對比圖。其中“v*”代表加速度積分后得到的數據，“v”表示未積分的數據。發現節點N28的加速度積分得到的速度與撞擊速度之間的差異以及積分位移值和靶板形變之間的差異，均隨著加載初速度的增加而減小。

非撞擊端中心節點N48364處加速度積分后的速度和撞擊速度的對比如圖11所示，圖12所示為加速度二次積分后的位移和靶板形變對比。“v*”代表加速度積分后得到的數據，“v”表示未積分的數據。

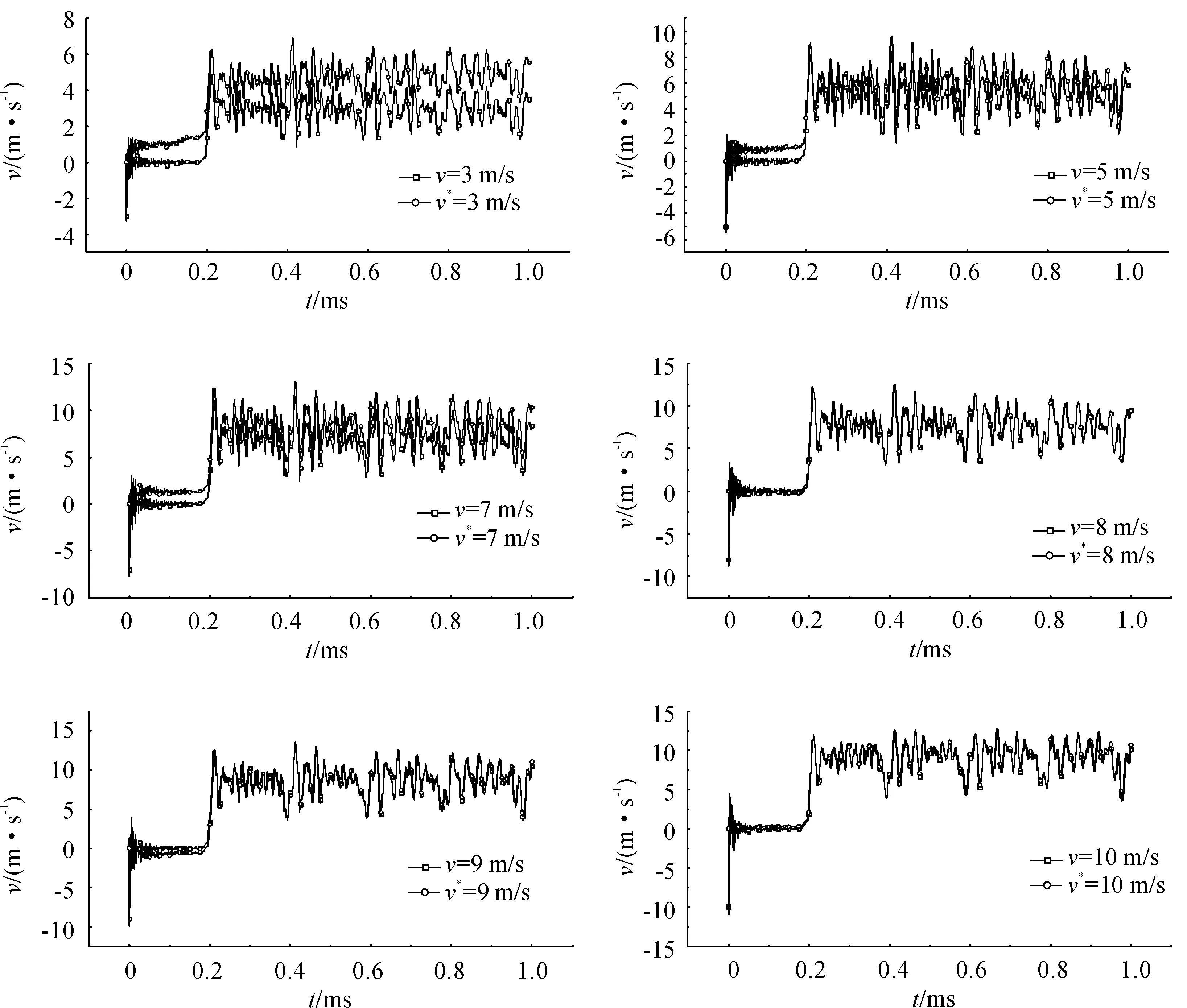
圖9 節點N28加速度積分后速度和撞擊速度

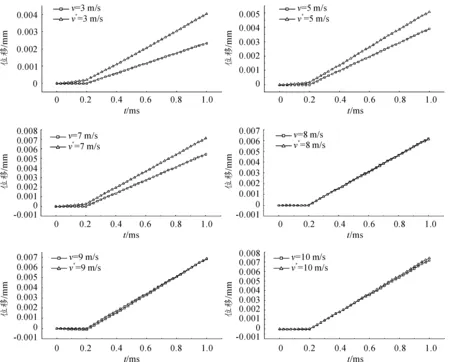
圖10 節點N28加速度積分后位移和靶板形變

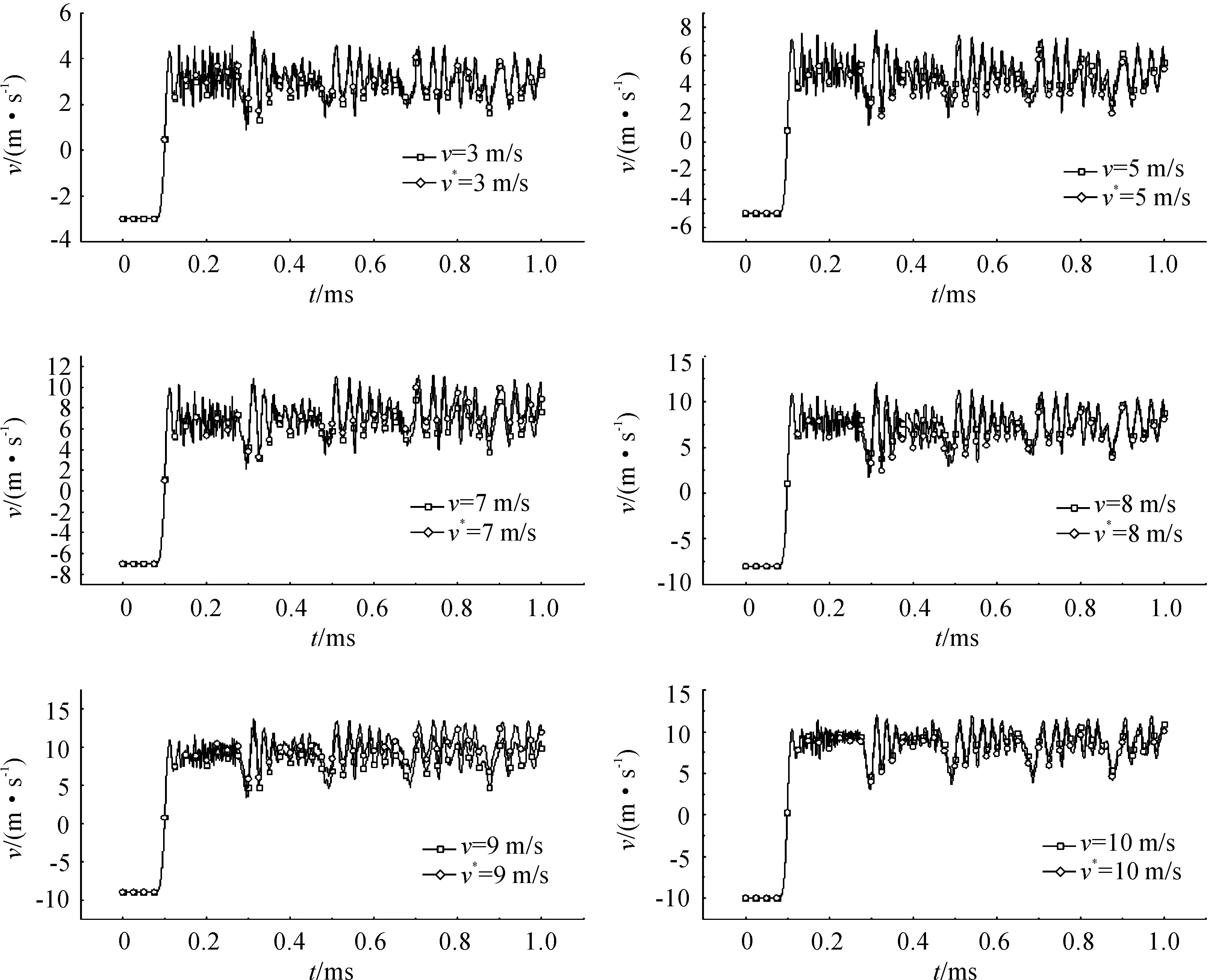
圖11 節點N48364加速度積分后速度和撞擊速度

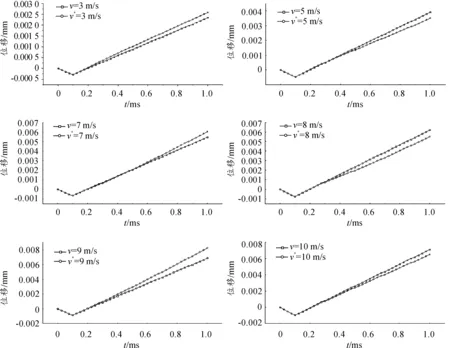
圖12 節點N48364加速度積分后位移和靶板形變

發現節點N48364加速度積分后得到的速度以及位移與加載初速度和靶板形變均能較好地吻合。說明在低速碰撞情況下，彈尾安裝加速度傳感器，采集的信號經過一次和二次積分后，得到的速度和位移應能很好的符合實際測量值，也就意味著此時所測量的加速度信號是準確可用的。由此可以推測，在中、高速侵徹下，過載信號積分值與實際值之間有較大偏差的原因很有可能是因彈體在侵徹過程產生的應力波嚴重影響了過載信號測量的準確性，為了提高過載信號測量的準確性，應采取措施降低或隔離應力波的影響，如在過載記錄儀中引入泡沫材料。

4 結論

1) 在長桿彈材料的彈性極限范圍內，低速撞擊過程中的平均加速度值隨加載速度的增加而提高，端面節點的加速度峰值亦隨加載速度的增大而增大，加速度峰值提高了一個量級。通過本次數值模擬實驗，為今后進行侵徹實驗提供了一定的理論支持，為加速度傳感器的安裝提供可參考的指導意義。

2) 低速碰撞情況下加速度信號經一次和二次積分后，得到的速度和位移與實際對應數據的差值很小。