基于ANSYS Workbench的搖擺裝置模態和瞬態分析

□余楊杰 □熊瑞平 □黃文強 □喬治

四川大學制造科學與工程學院 成都 610065

1 問題的提出

核能作為一種重要的能源，主要應用于軍事和發電領域。燃料組件是核能裝置非常重要的組成部分。燃料組件應用于不同場合時，可能產生不同程度的變形。一旦燃料組件發生較大的變形，則會影響控制棒的插入，導致卡棒，危及核能裝置的安全運行[1]。燃料組件應用在艦艇上時，會隨著艦艇的晃動而晃動。在晃動過程中，燃料組件可能出現變形。當燃料組件晃動的頻率接近自身固有頻率時，燃料組件甚至會出現較大的變形，對性能和壽命產生較大的影響。

針對上述問題，筆者結合燃料組件的擺動工況，設計了一種模擬燃料組件在艦艇上的搖擺裝置。首先對搖擺裝置進行動力學分析，確定了搖擺裝置的驅動變力矩。然后對搖擺裝置的擺動特性進行分析，研究搖擺裝置在擺動過程中的變形量和共振問題。最后對搖擺裝置整體進行瞬態分析，保證搖擺裝置結構的可靠性[2]。

2 動力學分析

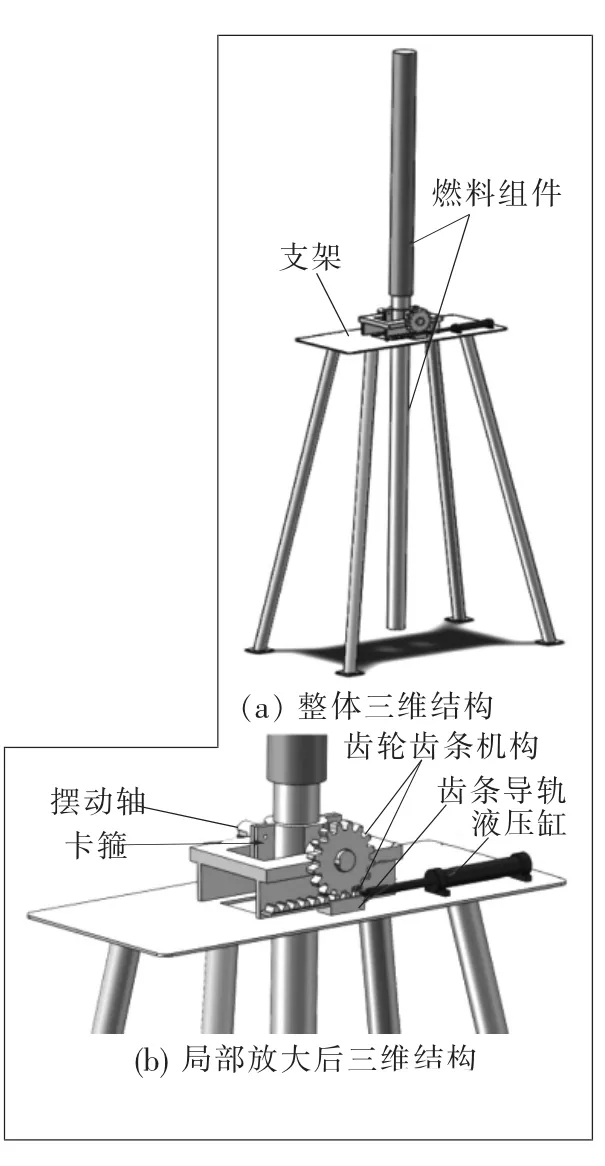
▲圖1 搖擺裝置三維結構圖

圖1所示為搖擺裝置的三維結構圖。圖1中上下兩段直徑不同的圓柱棒為燃料組件，燃料組件下段通過卡箍箍緊，在卡箍端面中心焊接擺動軸，燃料組件、卡箍和擺動軸共同構成擺動件。擺動軸放置在支架上，通過驅動裝置驅動擺動軸，使擺動件在支架上來回擺動。驅動裝置由齒輪齒條機構、齒條導軌、液壓缸等組成，通過液壓缸帶動齒輪齒條機構中的齒條沿著導軌來回運動，進而帶動齒輪轉動，最終使與齒輪相連的擺動軸同步轉動。根據燃料組件實際擺動情況，確定擺動件的擺動中心，將擺動件的擺動軸安裝在燃料組件下段距離過渡端面0.325 m處，擺動軸的直徑初定為0.1 m。搖擺裝置結構尺寸如圖2所示。

已知搖擺裝置存在三種比較危險的工況，這三種工況下的擺動角度和時間滿足正弦關系。搖擺件的擺角 θ為 3°、7.5°、22.5°，對應的擺動周期 t依次為 12 s、24 s、40 s[3]。

根據擺動件的三維模型，借助計算機軟件求得擺動軸到質心的距離為0.822 m。由于搖擺裝置的運動為簡諧運動，因此其擺長L=0.822 m，擺動周期T′為：

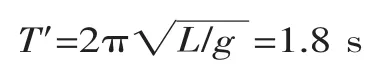
式中：g為重力加速度，g=9.8 m/s2。

可見，搖擺裝置自由無阻尼狀態下的擺動周期遠小于實際工況下的最小擺動周期。為了模擬搖擺裝置的真實運動，需要施加一個額外的驅動變力矩，使搖擺裝置的擺角和周期滿足要求。對搖擺裝置擺動件進行受力分析，如圖3所示。圖3中FN為擺動件所受支撐力，G為擺動件自身重力，Tf為擺動件所受摩擦阻力矩，T為擺動件驅動變力矩。

擺動過程中，擺動軸處的摩擦阻力矩很小，且數值不確定，為簡化計算，將其忽略，則擺動件驅動變力矩為：

式中：m為擺動件質量；J為擺動件轉動慣量；α為擺動件角加速度。

三種工況下的角位移函數分別為：

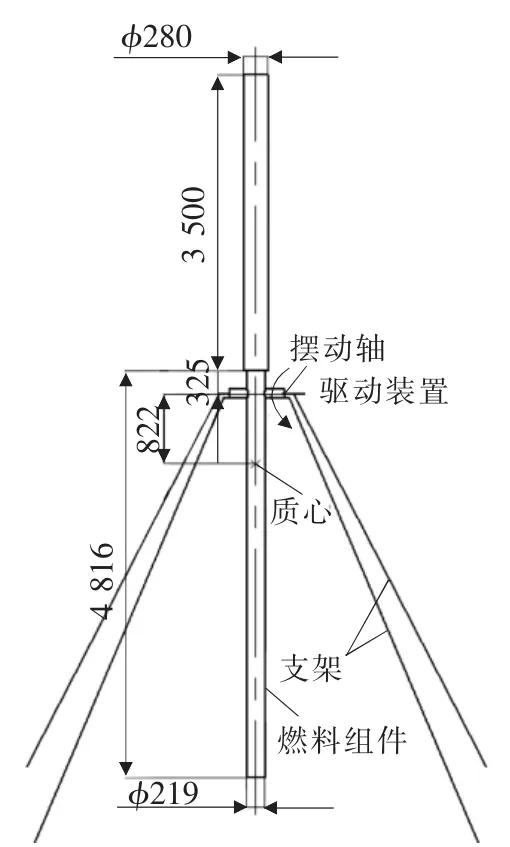
▲圖2 搖擺裝置結構尺寸

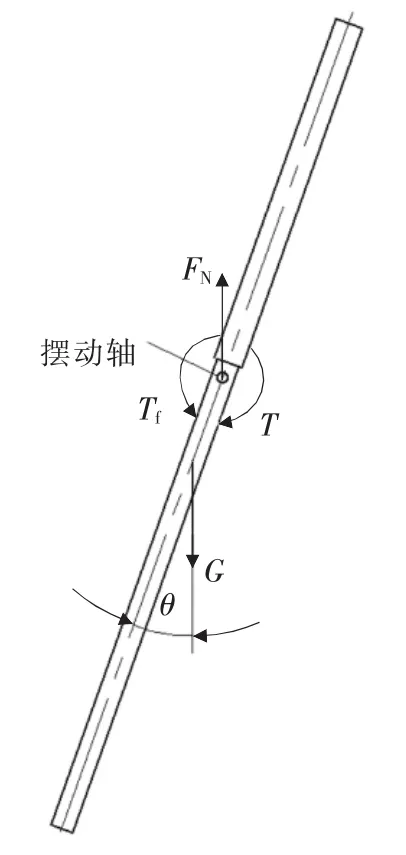
▲圖3 擺動件受力分析

對角位移函數求二階導數，可得角加速度函數[4]：

通過軟件求得擺動件的轉動慣量J=11 991 kg·m2，聯立式（2）～式（7），可求得三種工況下擺動件所需施加的驅動變力矩：

3 有限元建模

應用ANSYS Workbench軟件對搖擺裝置進行模態和瞬態分析，需要建立搖擺裝置的三維模型。應用SolidWorks軟件建立搖擺裝置的三維模型，通過SolidWorks與ANSYS Workbench的接口，將模型導入ANSYS Workbench，進行搖擺裝置的有限元分析。

由于驅動裝置只對擺動軸提供一個驅動力矩，且其質量較小，因此為了減少計算量和求解時間，將驅動裝置用一個外力代替，其提供的驅動變力矩直接施加在擺動軸上[5]。

3.1 材料特性

由于燃料組件的實際材料構成非常復雜，因此筆者對其材料構成進行簡化替代，上段材料采用鋁合金，下段材料采用結構鋼。搖擺裝置的其它結構，包括卡箍、擺動軸及支架同樣采用結構鋼材料。擺動過程中受力部位主要集中在卡箍及支架上，所以在對燃料組件進行有限元分析時，主要考慮結構鋼的材料特性能否滿足要求。結構鋼為45號鋼，其彈性模量為200 GPa，泊松比為 0.3，密度為 7 800 kg/m3[6]。

3.2 網格劃分

網格劃分是建立有限元模型的重要環節，網格劃分的質量對模型有限元分析結果的準確度和速度有重要影響。對搖擺裝置進行自由網格劃分，燃料組件單元類型為Solid187，卡箍、擺動軸及支架單元類型為Solid186。此外，擺動軸、螺栓連接處及支架凸臺根部結構強度可能較弱，在自由網格劃分的基礎上對這幾處網格進行局部加密細化。劃分網格后，搖擺裝置的網格數為 109 314，節點數為 215 362[7]，有限元模型如圖 4所示。

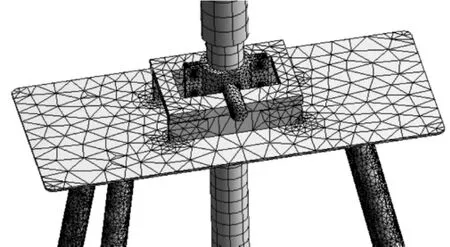
▲圖4 搖擺裝置有限元模型

▲圖5 搖擺裝置振型

4 模態分析

在搖擺裝置有限元模型建立完成后，對其進行模態分析，得到搖擺裝置的振動特性，包括固有頻率和振型，判斷搖擺裝置在擺動過程中是否會發生共振，同時也為瞬態動力學分析奠定基礎。

在分析時，支架處于固定狀態，對支架底部的四個面施加固定約束。對擺動軸施加圓柱面約束，使其徑向和軸向固定，圓周方向處于自由狀態。對于卡箍連接的螺栓處，用僅有壓縮面的約束代替螺栓作用。在約束添加完成后，還需對搖擺裝置施加預應力，包括卡箍處及驅動裝置處的預應力。

提取前十二階固有頻率，對應的最大變形和振型見表1。部分階數振型如圖5所示[8]。

對搖擺裝置各階固有頻率和振型進行分析。

搖擺裝置的前四階振型變形主要位于燃料組件上，且最大變形都位于端部。搖擺裝置的五至十二階振型變形主要集中在支架上，最大變形位于支架立柱中間位置處。

搖擺裝置的振型與其對應的固有頻率呈高度關聯，各階的固有頻率越接近，對應的振型也越相似。

搖擺裝置振型的最大變形理論上應隨固有頻率的增大而增大，但表1數據并非如此，分析其原因，一是最大變形可能出現在兩根立柱上，則該振型的最大變形量可能小于低階固有頻率對應振型的最大變形量；二是出現最大變形位置的面積較大，則該高階振型對應的最大變形量可能小于低階頻率對應振型的最大變形量。

搖擺裝置三種工況下的擺動周期分別為12 s、24 s、40 s，則最大擺動頻率為1/12 Hz，遠小于一階固有頻率6.87 Hz，因此，搖擺裝置在擺動過程中不會發生共振[9-10]。

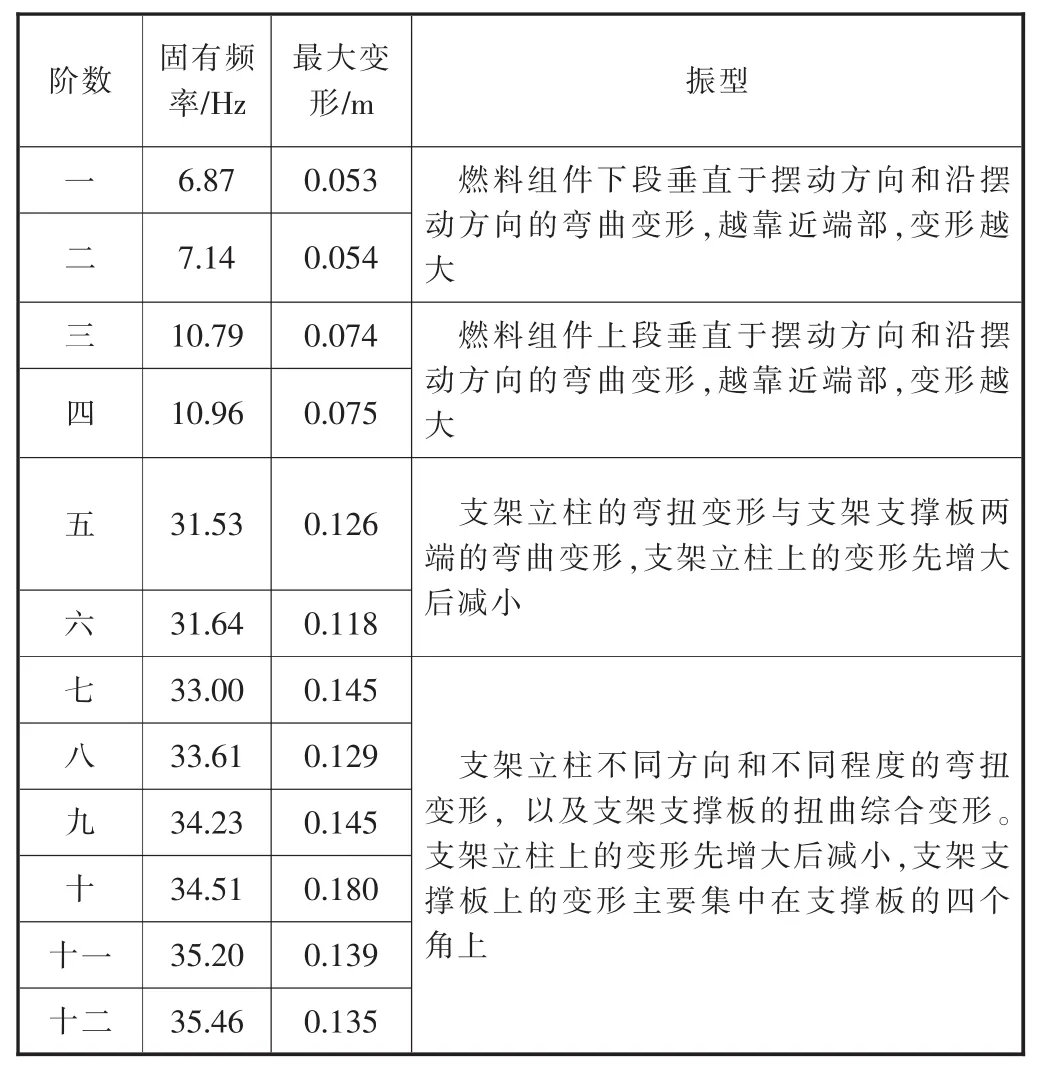
表1 前十二階固有頻率值

5 瞬態分析

雖然對搖擺裝置進行模態分析得出不會發生共振的結論，但仍需進一步對搖擺裝置進行瞬態分析，確保搖擺裝置整體結構設計的可靠性。在瞬態分析過程中，對搖擺裝置添加的約束與模態分析相同。在約束添加完成后，還需在ANSYS Workbench中施加重力。重力方向為-Y軸，同時對擺動件施加旋轉加速度。驅動裝置用一個外力代替，作用在支架支撐板上，然后在擺動軸上施加驅動變力矩。

在動力學分析過程中已求得三種驅動變力矩，則可以確定對應的函數曲線，如圖6所示。

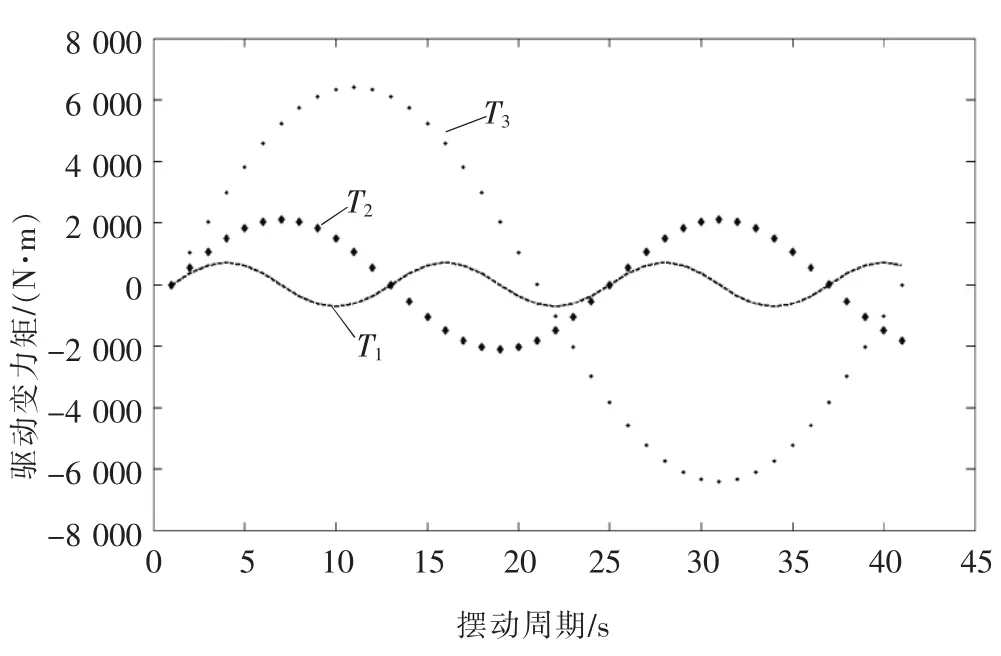
▲圖6 驅動變力矩函數曲線

由圖6可知，驅動變力矩T3的幅值最大，對搖擺裝置結構強度的影響也最大。筆者在驅動變力矩T3作用下進行瞬態分析，計算求解搖擺裝置的應力和最大變形。

對搖擺裝置進行瞬態分析后，提取其在驅動變力矩T3作用下的最大應力圖和總變形圖，分別如圖7、圖8所示。由圖7可見，最大應力為41.5 MPa；由圖8可知，最大總變形為811 μm。

搖擺裝置的最大應力位于卡箍螺栓連接處，最大總變形位于支架立柱中間位置處，兩者出現在不同的位置，原因應該與搖擺裝置不同位置的受力、結構尺寸差異及結構外形設計有關。

在對搖擺裝置施加驅動變力矩T3時，最大等效應力為 41.5 MPa，小于材料的許用拉應力（250 MPa）；最大總變形量為811 μm，相對于搖擺裝置整體尺寸而言很小，滿足結構安全要求。

6 結論

針對燃料組件在艦艇上的擺動問題，筆者設計了一種用于模擬的搖擺裝置。對搖擺裝置進行動力學分析，得出所需施加在搖擺裝置上的驅動變力矩，并在此基礎上應用ANSYS Workbench軟件對搖擺裝置進行模態和瞬態分析。結果表明，搖擺裝置在擺動過程中不會發生共振，且其結構設計安全可靠，滿足強度要求。筆者研究對燃料組件在艦艇上的應用有一定參考價值。

▲圖7 搖擺裝置最大應力圖

▲圖8 搖擺裝置總變形圖