基于模型修正的特殊行車狀態下橋梁動態響應研究

龍關旭,高貴杰,馮 宇,黃平明

長安大學公路學院,陜西 西安 710064

現行的荷載試驗規程中規定，橋梁動載試驗宜首選無障礙行車，而有障礙行車和制動試驗并不是必須項[1]，但在橋梁實際運營過程中，由于橋面不平整度、橋面雜物等原因產生的車輛跳車現象時有發生，而且隨著交通量的增大，橋上駕駛環境的愈加復雜，車輛緊急制動問題也逐漸被學者們所關注。

對于車輛過橋產生的動力響應研究，最初多集中在車輛勻速行駛方面[2-4]，而針對特殊行車狀態下的研究相對較少，例如跳車、剎車、加速行駛等，且存在計算模型簡單、參數分析不足等問題[5]。鄧露[6]基于三維車橋振動模型研究了汽車制動對橋梁的沖擊作用，結果發現車輛制動下產生的沖擊系數明顯大于勻速行駛狀態。蒲軍平[7]考慮了車輪處的摩擦力與剎車制動力共同作用，對車橋耦合振動現象進行了數值模擬。陳斌[8]針對懸索橋采用7自由度平面分析模型，研究了行車速度，橋面不平順，剎車制動三種因素影響下的動力響應。

基于目前研究狀況，綜合考慮橋梁模型的準確性與實橋驗證，本文以許塘橋為依托，對橋梁初始模型進行模型修正，得到反映橋梁真實狀態的有限元模型，并對跳車試驗和剎車試驗進行模擬與實測，進而對特殊行車狀態下的橋梁動態響應展開研究。

1 有限元模型修正方法及流程

在橋梁結構的分析過程中，按照設計圖紙來建立橋梁有限元模型，但這樣建立的有限元模型往往不能反映實際結構的真實狀態，這就需要對建立的有限元模型進行修正。本文采用基于敏感度的參數型修正方法，首先根據設計參數建立初始有限元模型，其次基于敏感分析確定需要修正的參數，并根據現場實測值和理論值的誤差來構建目標函數，最后利用ANSYS進行零階優化迭代直至收斂而得到最優解[9]，具體流程圖如圖1所示。

2 有限元模型修正

2.1 橋梁概況及初始有限元模型建立

以浙江省長興縣許塘橋為工程實例，該橋采用單跨下承式混凝土系桿拱結構，單跨71.96 m，計算跨徑70 m，橋面寬度為9.3 m，橋面凈寬為7.0 m，雙向兩車道。該橋設計荷載為公路-Ⅱ級，計算矢跨比為1/6，橋梁立面圖如圖2所示。

根據橋梁原設計圖紙、結構特點及橋梁結構現狀，并考慮荷載加載位置和有限元模型修正的實現及目的，采用有限元模型ANSYS對該橋建立初始有限元模型，如圖3所示。其中拱圈、系梁、吊桿，橫梁及虛擬縱梁均采用beam44梁單元進行模擬，全橋共劃分557個節點，850個單元。材料的初始質量密度為2420 kg/m3，彈性模量取3.45×1010Pa。

圖2 許塘橋立面圖Fig.2 Elevation of Xutang bridge

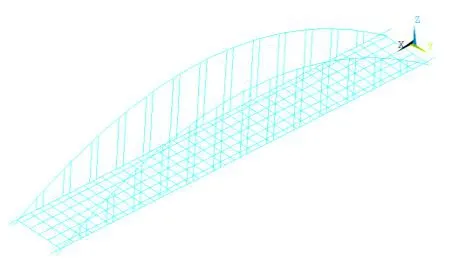
圖3 許塘橋初始有限元模型Fig.3 Initial finite element model of Xutang bridge

2.2 現場試驗

對許塘橋的固有振動特性進行了現場測試，試驗通過加速度傳感器拾取大橋各測點的環境振動響應，測試結構的固有頻率和振動模態。模態測試縱向布置在八分點截面處，對稱布置14個測點，測試三向（豎向、橫向、扭轉）振動特性。

2.3 有限元模型修正

首先進行設計參數選擇，頻率靈敏度分析結果見圖4，給出了豎向前三階（V1、V2、V3）、橫向前三階（H1、H2、H3）和扭轉前兩階（T1、T2）頻率靈敏度變化，各參數對結構動力特性均有不同程度的影響，故選定系梁彈性模量Et、拱肋彈性模量Er、吊桿彈性模量Es、橫梁彈性模量Ec、系梁質量密度Dt、拱肋質量密度Dr、吊桿質量密度Ds、橫梁質量密度Dc作為模型修正參數。

根據設計的有關資料和各個參數靈敏度的分析，設定修正參數的范圍，修正范圍主要以初始值的±10%～±20%控制，在本算例中，基于動力測試數據進行有限元模型修正，采用關于聯合頻率和模態相關性系數MAC構造目標函數，見式（1）。

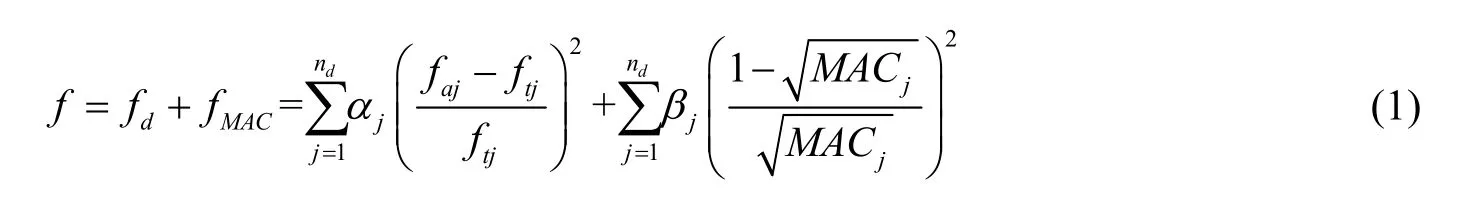
式中fd是基于頻率的目標函數，fMAC為基于MAC的目標函數，αj和βj是權重系數，反映了特征值和MAC相關函數之間的不同的比重，本橋系數均定義為1。nd為模態階數，faj和ftj是第j階理論和試驗的頻率，MACj表示第j階的模態保證準則值，表示第j階試驗和理論振型的相關程度。

圖5給出了采用零階優化算法的優化迭代過程，從圖中可以看出優化迭代初始階段目標函數值浮動跳躍較大，第19次后目標函數值基本趨于平穩，可視為函數已收斂，獲得了最優解。

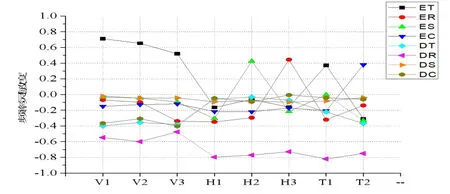
圖4 參數靈敏度分析Fig.4 Parameter sensitivity analysis

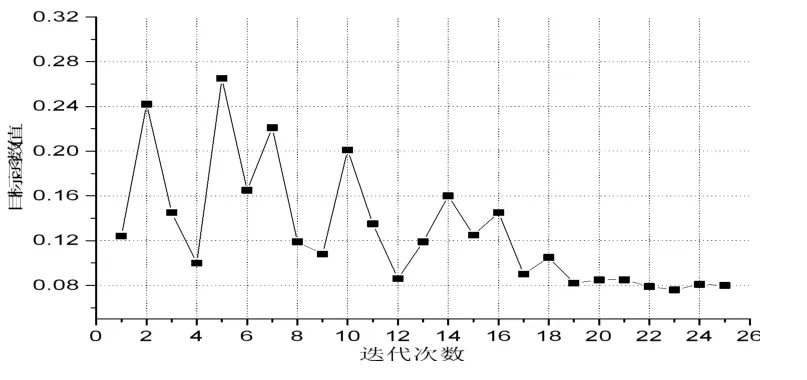
圖5 優化迭代過程Fig.5 Optimizing iterative process

模型修正前后，許塘橋動力特性對比詳見表1，可以看出修正后的橋梁頻率與實際測得的頻率更為接近，MAC也得到了有效的提升。

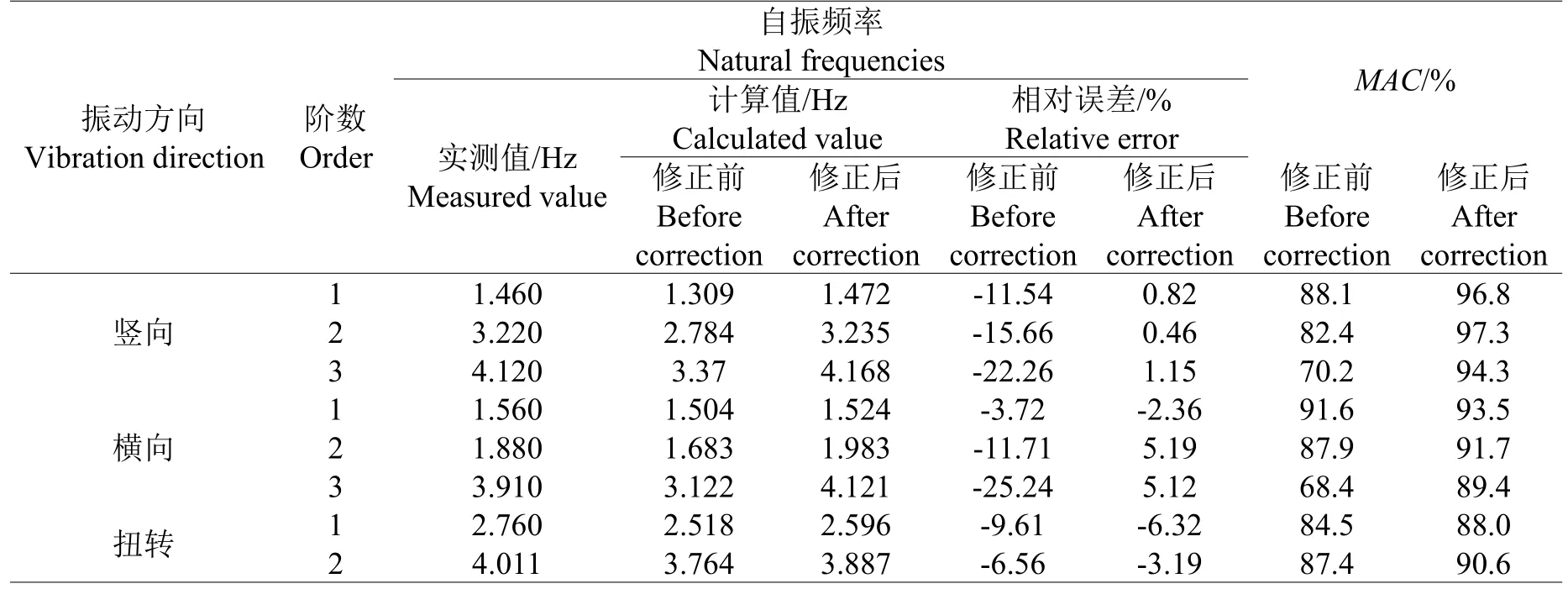
表1 有限元模型修正前后自振特性對比Table1 Comparison of natural vibration characteristics before and after finite element model modification

3 特殊行車狀態下橋梁動態響應

3.1 現場動載試驗

通過前文的有限元模型修正，獲得了能夠反映結構真實狀態的基準有限元模型。基于修正后的模型，對許塘橋進行了動載試驗，包括無障礙跑車、跳車和剎車試驗，測試結構的動力響應并進行驗證。選擇跨中截面作為動應變測試截面，測點布置在系梁上，同時在跨中橋面布置DH610三向加速度傳感器，用以拾取特殊行車狀態下加速度信號。

3.2 跳車試驗

跳車試驗在橋面跨中位置放置半弓形障礙物，高度分別選用5 cm、7 cm和10 cm，采用30 t三軸（雙后軸）汽車作為試驗車輛，以0 km/h(原地跳車)、10 km/h、15 km/h和20 km/h的速度行駛過障礙物，采集跨中位置動力響應。

針對跳車試驗，主要關注橋梁豎向振動特性。以5 cm高的障礙物0 km/h原地跳車為例，豎向加速度隨時間變化如圖6所示，基本能看出試驗車輛三個輪軸過障礙物產生沖擊的現象。圖7給出了不同速度、不同障礙物高度的豎向加速度極值變化趨勢，可以看出除個別點跳躍點外，隨著障礙物高度的增大和車速的增大，豎向加速度極值整體呈現變大的趨勢。

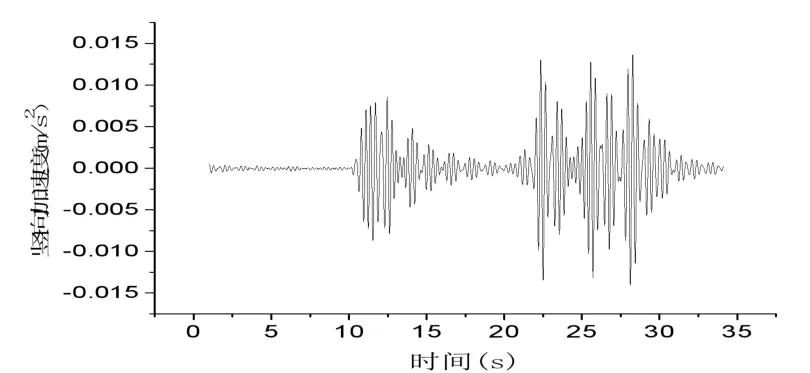
圖6 跳車試驗豎向加速度曲線Fig.6 Vertical acceleration curve of bumping test

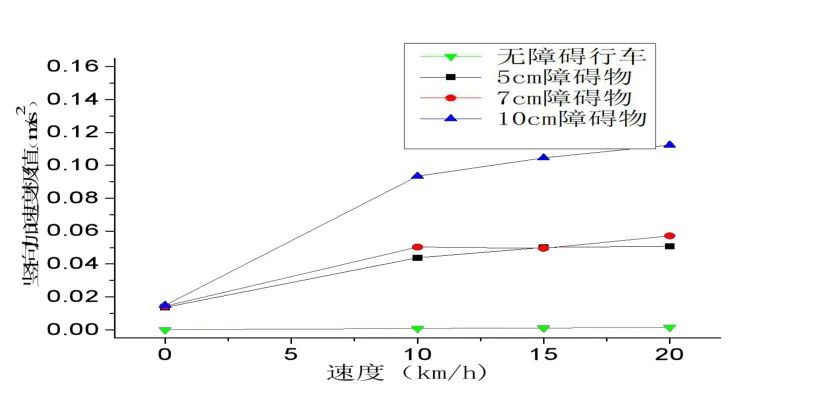
圖7 豎向加速度極值變化Fig.7 Vertical acceleration extrema variation

根據實驗過程中測得的動應變數據，對橋梁沖擊系數進行計算，詳見表2，從表中可以看出相比于無障礙行車，跳車情況下橋梁沖擊系數明顯增大，可以達到1.80以上。

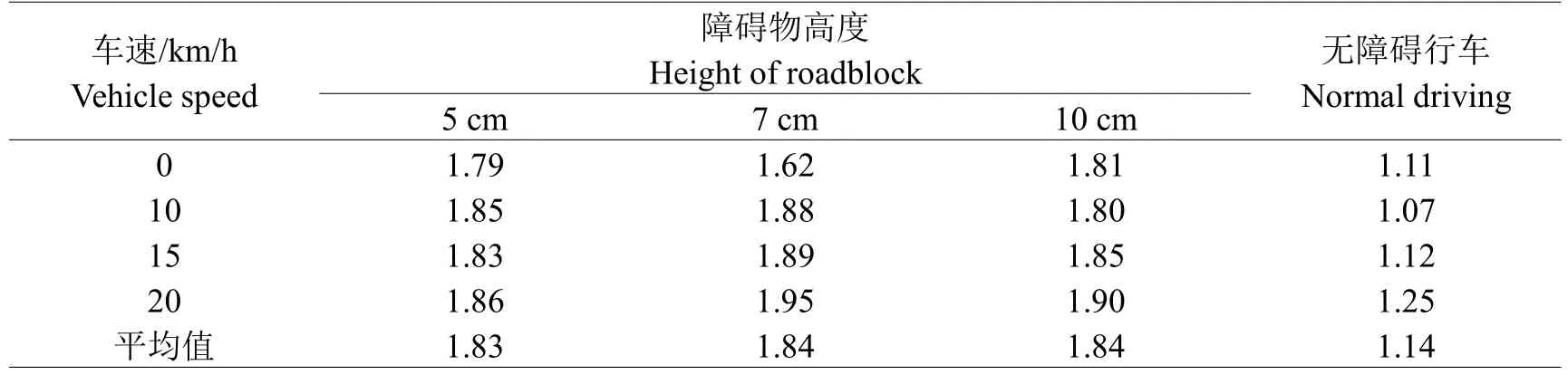
表2 不同工況下沖擊系數Table 2 Impact coefficient under different conditions

3.3 剎車試驗

剎車試驗將模擬前方出現交通事故情況，車輛發生緊急制動。采用與跳車試驗相同的30 t三軸（雙后軸）加載車，控制的主要參數有：（1）剎車初始速度：10 km/h～40 km/h（以10 km/h為一個間隔）；（2）剎車位置：L/4、L/2、3L/4。由于現場控制剎車加速度難度較大，因此通過控制剎車距離來控制剎車減速度大約在3.5 m/s2，并使用手持式速度儀核對剎車初始速度。

針對剎車試驗主要研究橋梁縱向振動特性。以30 km/h速度跨中剎車工況舉例，圖8給出了主梁跨中縱向應變的時程變化曲線，可以看出隨著車輛的駛入縱向應變逐漸增大，在16 s左右時達到最大值，相比于正常跑車，縱向應變有一個明顯的突變現象，極大值增加約20%左右，可見剎車對結構縱向響應有明顯影響。圖9為主梁跨中縱向加速度時程曲線，理論值和實測值變化趨勢基本一致，理論值結果偏大。

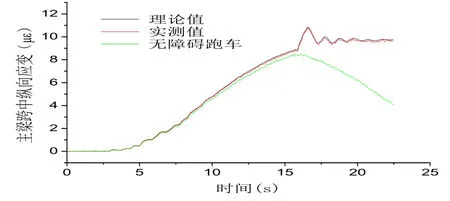
圖8 剎車試驗縱向應變曲線Fig.8 Longitudinal strain curve in braking test

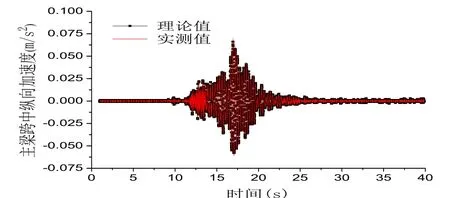
圖9 縱向加速度曲線Fig.9 Longitudinal acceleration curve

圖10和圖11分別對不同速度下，不同剎車位置橋梁響應的進行了對比。由圖10可看出，主梁縱向加速度極值隨車速的增加而變大，且L/2處和3L/4處剎車響應較為接近，L/4處剎車橋梁響應增大趨勢明顯，梁端縱向位移隨車速也呈現出相同的規律。

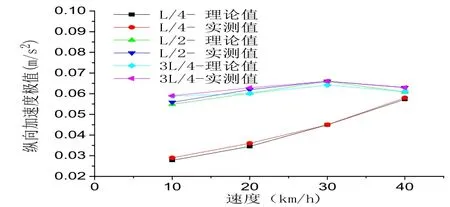
圖10 縱向加速度極值變化Fig.10 Extreme changes of the longitudinal accelerations

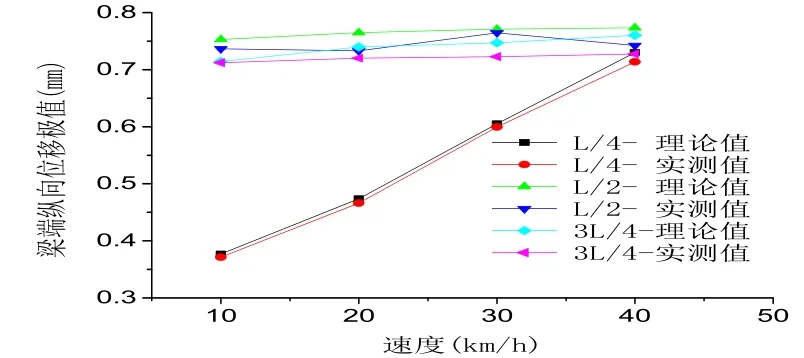
圖11 縱向位移極值變化Fig.11 Extreme changes of the longitudinal displacements

4 結 論

本文利用模型修正獲得了橋梁基準有限元模型，并通過跳車和剎車試驗采集主要動力參數，將實測數據與理論數據對比分析，得出以下主要結論：

（1）經過模型修正后的基準有限元模型與初始模型相比，其動力特性與實測數據吻合度更好；

（2）跳車工況下，跨中加速度峰值隨著障礙物高度和行車速度的增加而變大，且沖擊系數達到1.84左右；

（3）剎車工況下，實測與理論跨中動應變和縱向加速度時程變化趨勢基本一致，隨著車速的增加縱向加速度極值和梁端縱向位移極值也逐漸增大，且L/2和3/4處剎車動力響應明顯大于L/4處，說明車輛在橋梁后半段剎車能引起更大的縱向響應。