基于高光譜數據和SVM方法的土壤鹽漬度反演

池 濤,曹廣溥*,李丙春,孜克爾·阿不都熱合曼,王文龍

1.上海海洋大學 信息學院,上海 201306

2.喀什大學 計算機科學與技術學院,新疆 喀什 844006

土壤鹽漬化是一種常見但危害巨大的土壤退化現象，會降低農作物的產量，嚴重時農作物無法生長而且會破壞當地生態環境。中國領土廣泛，不同區域的地質、氣候、領海情況不同，造成了中國鹽漬土種類豐富，很難定量分析。國內外對鹽漬化土壤光譜機理[1-4]和模型反演[5-8]已進行了深入研究，形成了很多研究成果，但這些成果大多體現在定性分析和論文描述中，至今無應用于實際儀器儀表記錄。

本研究是基于不同鹽度土壤反射光譜數據分析，采用多元線性回歸、BP神經網絡和支持向量機三種在數據回歸領域中使用較廣的兩種算法，對土壤含鹽量進行非線性定量擬合，代碼通過MATLAB編程實現。創新點是在PC機中驗證機器學習算法在土壤含鹽量預測領域的適用性，以便于后期移植到實際的儀器儀表制作中。

1 樣本采集與數據處理

1.1 樣品的采集

實驗以不同區域的土壤為研究對象，一類供試土樣采自上海市濱海地區，二類供試土壤采自新疆省喀什區域，隨機土樣共270個（上海鹽土150個，喀什鹽土120個）并將每個土樣分為兩份，一份土樣用于含鹽量檢測，一份用于土壤光譜測定。

1.2 土樣含鹽量檢測

本研究使用重量法檢測土壤含鹽量，土壤進過篩孔、溶解、去有機質、風干和稱重等過程，測得土壤樣本含鹽量情況如下表：

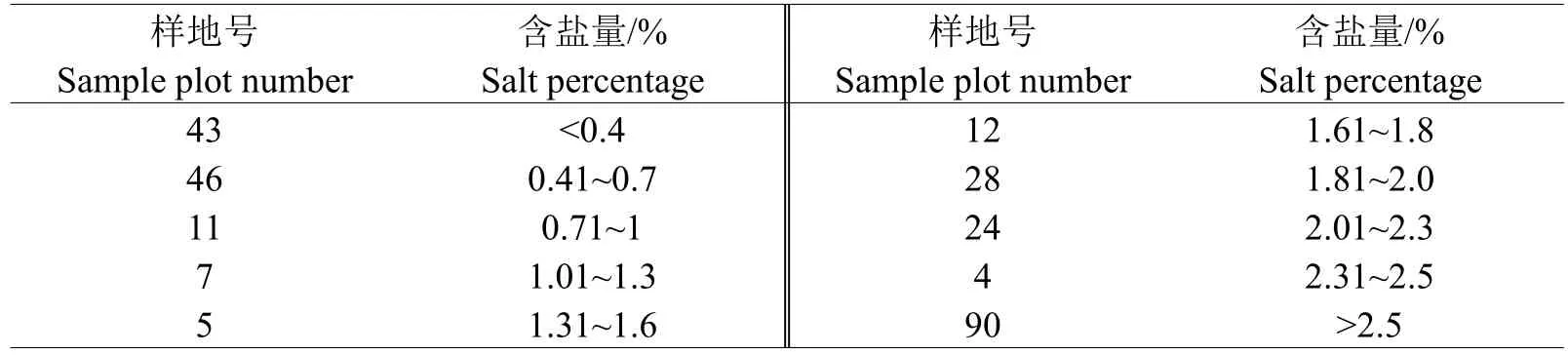
表1 土壤含鹽量樣地統計表Table 1 Statistics tables of soil salinity sample plots

1.3 土樣光譜測定與處理

土壤光譜測定使用了Field Spec Pro FR（美國Analytical Spectral Devices公司）光譜儀，波長范圍為350～2500 nm。在暗室中測定樣本光譜，350～1000 nm波段光譜分辨率為3 nm，1000～2500 nm波段光譜分辨率為10 nm，采樣間隔都是1 nm。光源使用了1000 W的鹵素燈，光譜儀傳感器探頭放置在土壤樣本的正上方，探頭接收的樣本區域應遠小于土壤樣本的整體面積，確保探頭接受的所有反射光譜都是來自土壤樣本的[9]。重復采樣土壤樣本光譜曲線并取均值作為處理好實驗數據供后面實驗使用。

在MATLAB中對采集到的光譜曲線進行去噪處理，處理后的光譜曲線如圖1。

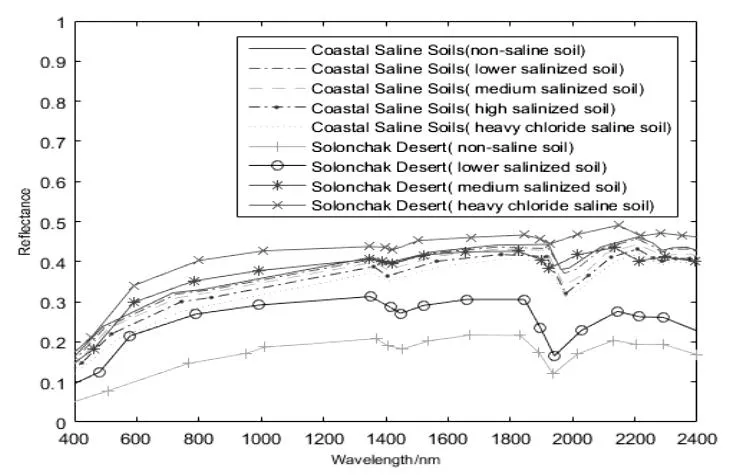
圖1 不同鹽漬土光譜反射率Fig.1 Spectral reflectance of different saline soils

兩種供試土壤的土壤類型不同，第一類土壤采集自上海臨海區域的鹽土，土壤中的鹽類大多是氯化鹽，如NaCl和MgCl2，因為氯化物吸收水分的能力強導致氯化鹽土中水分較高，所以該類土壤的光譜反射率會隨著鹽漬化程度的增加而降低。而第二類供試土壤采集自新疆的喀什戈壁地區，由于天氣干燥，土壤含水量極低而出現了鹽結晶溢出的現象，這也導致了二類土壤的光譜反射率會隨著鹽漬度程度增加而增加。

由于光譜波段數量較多，直接對原始數據進行擬合實驗會造成實驗模型復雜且運行效率低，所以需要采集一些特征值來表征某個土壤樣本的整條光譜曲線。本研究選取鹽漬土在350 nm、700 nm、1350 nm、1400 nm、1500 nm、1850 nm、2050 nm、2200 nm和2500 nm的光譜反射率曲線值以及土壤表征參數（特征波段斜率）：

Xa(350～700 nm)，Xb(700～1350 nm)，Xc(1350～1400 nm)，Xd(1400～1500 nm)，Xe(1500～1850 nm)，Xf(1850～2050 nm)，Xg(2050～2200 nm)，Xh(2200～2500 nm)。

通過這種方法簡化后的17個參數，不但涵蓋了土壤光譜曲線的所有信息，而且可以避免樣本少輸入數據多而導致的擬合模型不穩定的問題。

2 鹽漬化反演模型的構建

2.1 多元線性回歸模型

多元線性回歸是一種常用的線性擬合方法，適用于自變量數量多的數據回歸中，因變量與多個自變量都存在相關性，然后通過回歸分析得出因變量與自變量的映射關系。多元線性回歸方法是農學數學分析最常用的方法，本研究對土壤光譜數據進行多元線性回歸，除去大于0.05大于顯著水平的輸入變量，得到土壤光譜數據與含鹽量的映射方程，擬合公式如下：

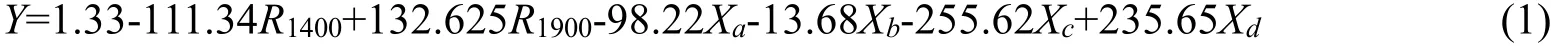
2.2 BP神經網絡模型

BP神經網絡(BPNN)是一種采用了誤差逆向傳播算法來訓練的前饋式神經網絡，如果已有神經元之間的權值和閾值正向傳播無法達到期望值，則反向傳播計算誤差大小來修改各節點的權值和閾值，逐步減小代價函數，使預測誤差降到預先設定的數值[10]。當誤差達到期望或者多次迭代后無法降低誤差，則BP網絡訓練完成，此時的BP網絡就是輸入與輸出之間的映射關系。

本研究中的BP神經網絡在MATLAB中實現，分為模型構建、自動訓練和結果預測三個過程，通過MATLAB自帶神經網絡實驗箱中的newff、train、sim三個函數來實現。將表征光譜曲線的17個參數作為BP神經網絡的17個節點，隱含層的數量在不斷實驗中確定，輸入層為土壤含鹽量一個節點。代碼實現過程如下：

其中：input是輸入的土壤光譜數據；output是土壤含鹽量；input_test是測試數據；BPoutput是預測結果。

通過mapminmax函數對輸入數據、輸出數據和訓練樣本數據進行歸一化，輸入層到隱含層使用S型對數函數logsig，隱含層到輸出層使用純線性函數purelin，通過多次實驗，選擇了收斂效果最好、誤差最小的trainlm作為訓練函數。訓練步數設置為100步，學習速率為0.1，理想誤差為0.00004。將土壤光譜數據作為輸入數據，土壤含鹽量作為輸出數據，訓練模型，在誤差達到理想誤差時或是多次迭代后誤差不在下降時，模型訓練結束，得到的權值閾值矩陣就是BP神經網絡模型。訓練完成之后，將訓練樣本導入輸出層，計算出預測結果并與實際結果相比較，得出BP神經網絡的誤差率。

由于BP神經網絡模型受訓練樣本數目影響較大，在小樣本實驗中，BP神經網絡易出現局部誤差大、模型不穩定等情況，所以本文對實驗進行了2個調整：

（1）從輸入的17個節點中挑選出6個權值貢獻率最大的節點作為輸入節點，減少了輸入節點的數量，簡化了BP神經網絡模型。

（2）加一個BP神經網絡模型用于土壤種類的分類，減少了土壤種類對模型精確度的影響。

修改后的模型如圖2。

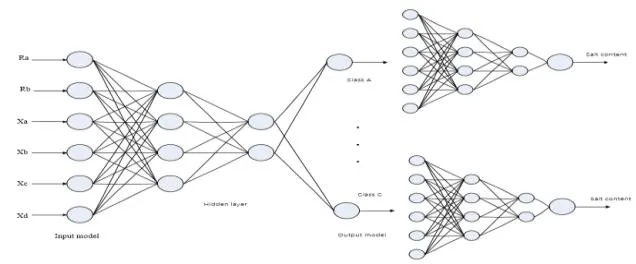
圖2 復合BP神經網絡模型Fig.2 Compound BPneural network model

2.3 SVM模型

支持向量機（Support Vector Machine）是Cortes和Vapnik于1995年首先提出的用來解決函數擬合的問題。支持向量機一般用于分類和回歸兩種情況，本研究中土壤鹽漬化反演模型就是使用支持向量機進行回歸。在使用支持向量機進行回歸時，需要調整的參數是懲罰參數c、不靈敏損失參數ε、核函數類型和核函數參數[11,12]。

控制支持向量機回歸的參數主要有懲罰參數c、不靈敏損失參數ε、核函數類型和核函數參數。c越大，表示經驗風險越小，即模型越復雜，泛化能力越差；c越小，模型越簡單，泛化能力越強，但可能犧牲了模型的擬合能力。ε用于修改支持向量的數量，ε越小，支持向量機數量越大，模型相對來說約復雜。已有學者研究表明，徑向基核函數在土壤鹽漬化反演模型中效果更好。因此，本研究的選擇徑向基（RBF）作為核函數，其表達式為：

式中：σ為核函數參數。

代碼實現流程如下：

支持向量機輸入輸出數據初始化、測試樣本和訓練樣本的設置與BP神經網絡模型的設置相同，然后通過libsvm-mat的網格參數尋優函數的調用，對懲罰參數c和核函數參數g進行最優值尋找。先進行參數粗略選擇，c的搜索范圍設置為10-5～1010，g的搜索范圍設置為10-5～105，迭代步長設置為1，然后進行參數精細選擇，c的搜索范圍設置為100～1010，g的搜索范圍設置為10-5～100，迭代步長設為0.3。參數選擇完成后，再利用回歸預測分析的最佳參數進行SVM模型訓練。

3 結果與分析

3.1 多元線性回歸、BP神經網絡和SVM模型對土壤含鹽量預測比較

本實驗采集鹽漬土光譜數據，處理后作為輸入數據，并檢測土壤含鹽量作為輸出數據，將這些數據分為訓練集和預測集來進行建模。

在多元線性回歸實驗中，除去大于0.05大于顯著水平的輸入變量后建立的模型擬合精度為76.8%，效果并不理想，這是因為多元線性回歸方法適用于線性數據的擬合，而土壤光譜數據是機理尚不明確的非線性數據，使用線性回歸方法處理難免會出現誤差較大的情況。圖二是BP神經網絡收斂過程，經過17步訓練，測試集誤差達到目標誤差以下，為4.036×10-5，但測試集誤差下降到5×10-4左右時就會出現反復迭代無法下降的情況，這是因為BP神經網絡模型對樣本數量要求較高，在小樣本實驗中，訓練集和測試集都會出現數量不夠，從而導致模型不穩定、測試集不具有普遍性、部分測試數據誤差較大的情況。圖三、圖四是支持向量機參數模糊、精確選擇結果，經過網格尋優得到的最優參數為c=9.849、g=0.0583，模型的擬合精度為99.4119%。從以上實驗可以看出，線性回歸方法、BP神經網絡和支持向量機都可以完成收斂任務，BP神經網絡和SVM的誤差收斂穩定，訓練、預測效果好。

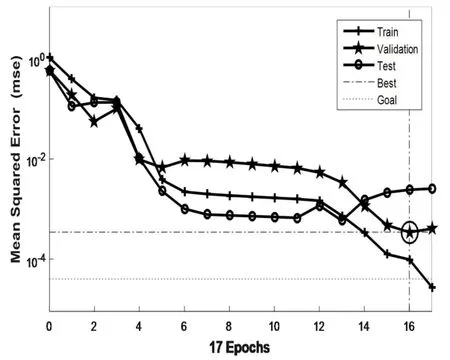
圖3 BP神經網絡均方差變化曲線Fig.3 Variation curve of BP neural network mean square error

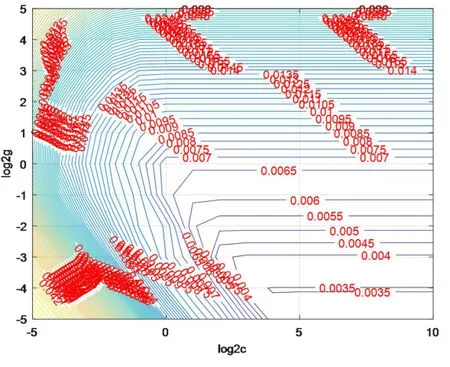
圖4 SVM參數模糊選擇結果Fig.4 SVM parameter fuzzy selection results

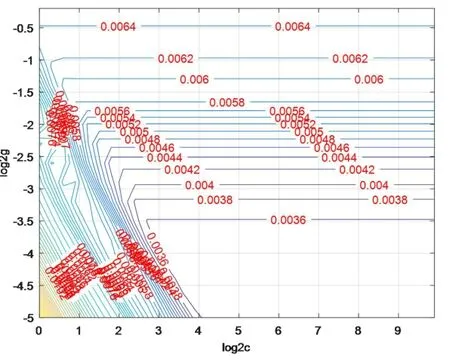
圖5 SVM參數精細選擇結果Fig.5 SVM parameters precision selection results

3.2 土壤鹽漬化預測模型對比

對實驗使用的三種模型進行誤差分析對比，對比結果如圖6。

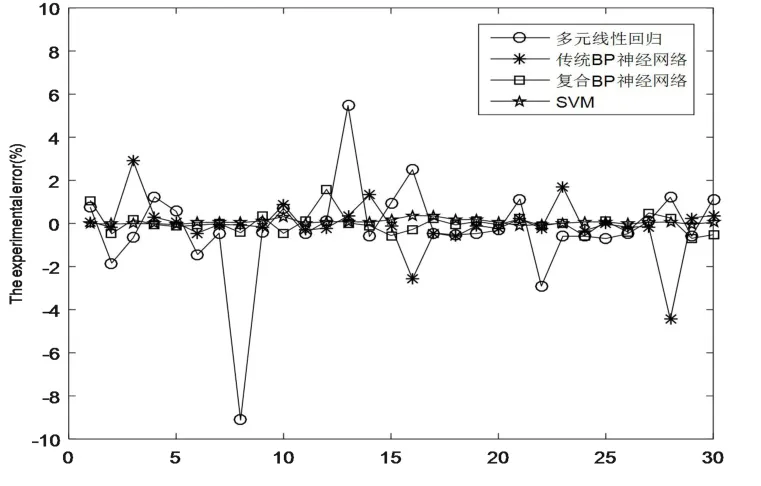
圖6 多模型誤差對比Fig.6 Multi-model error comparison

線性回歸方法最大相對誤差為912.32%，最小相對誤差為10.03%，由于個別測試值誤差巨大，所以導致平均相對誤差達到128.25%，這也說明線性回歸方法并不適用于土壤光譜數據這種復雜非線數據的擬合；BP神經網絡模型的最大相對誤差為444.68%，最小相對誤差為2.79%，平均相對誤差為67.45%，增加土壤分類功能的復合神經網絡模型的最大誤差為158.35%，最小誤差為0.55%，平均相對誤差為32.213%，比較而言，傳統的BP神經網絡還是有部分預測數據誤差較大的情況，百分35.84%的擬合精度也不理想，而改進后的復合BP神經網絡模型的擬合精度達到了67.78%，預測精度遠遠高于傳統BP神經網絡模型，說土壤種類對土壤光譜數據的影響較大，通過修改模型減少這種影響可以提高預測模型精度；SVM模型的最大相對誤差為37.341%，最小相對誤差為0.431%，平均相對誤差為9.253%，擬合精度明顯高于BP神經網絡模型，也達到了一個理想的精確度。之所以出現這樣的實驗現象，是因為BP神經網絡模型對訓練樣本數量要求高，需要對數據進行大量的預先處理，而且在調試過程中需要大量的調整技巧，并不適用與土壤含鹽量反演這樣的小規模數據實驗。支持向量機在這樣的小規模數據實驗中表現較好，因為支持向量機有著嚴格的數學理論作基礎，會先經過大量計算來求出全局參數最優解，省去了數據預處理的階段，并且可以有效避免神經網絡易出現的局部極值問題，因此支持向量機模型的預測精度會高于多元線性回歸模型和BP神經網絡模型。

4 結 論

本文以新疆喀什地區和上海沿海地區為研究區，采集了270個土壤樣品進行土壤鹽漬化預測研究。實驗選取了多元線性回歸模型、BP神經網絡模型和支持向量機模型來預測土壤含鹽量，探究這三種模型在土壤含鹽量預測中的適用性，結論如下：

（1）多元線性回歸方法在預測土壤含鹽量時，會出現個別預測結果誤差極大，整體預測精度也不高，不適用于復雜非線性數據的擬合實驗中；

（2）BP神經網絡模型受樣本數量影響較大，樣本數量不足會導致模型不穩定，所以會出現土壤類型對精度影響大的現象，經過改進后的BP神經網絡模型，實際實驗中均方誤差為32.213%，基本可以完成預測任務；

（3）SVM模型有著嚴格的數學理論基礎，在小樣本實驗中表現也更好，擬合精度達到99.4119%，在實際實驗中均方誤差為9.253%，預測結果非常理想。