以生為本 順學而教
——淺談《三角形的面積》的教學策略

浙江溫州市仰義第一小學 林志輝 林 迪

人教版數學以兩個完全一樣的三角形拼成一個平行四邊形的“雙拼法”為主要方法來推導三角形的面積計算公式，承接了平行四邊形的面積計算公式，公式表達和幾何直觀聯系緊密，易于學生聯系圖形和公式之間的關系。但求平行四邊形的面積時采用沿高剪開割補的轉化方法，學生又缺乏圖形拼組的經驗。因此，學生理解“雙拼法”不難，怎么想到“雙拼法”反而有難度。

一、從人教版教材探究學生的知識起點

人教版的圖形面積教學部分，以單位面積度量圖形為基本方法，以長方形為基礎圖形，依次將平行四邊形轉化為長方形，將三角形轉化為平行四邊形。但在轉化方法上卻經歷了圖形單側先割后補—圖形拼組這樣的跳躍。在教學如何計算長方形、平行四邊形的面積時都有用單位面積量一量、數一數、算一算的過程，而在教學三角形的面積計算公式時卻省略了格子圖和計算面積的過程，直接跳到了三角形面積計算公式的推導上。

將三角形轉化為已知圖形的方法較多，人教版教材中僅僅出現了“雙拼法”，其他方法需不需要介紹，學生是否要掌握，就很難取舍了。

二、通過動手操作探究學生的思維過程

教師為A、B兩個班共67名五年級學生（已經學習了平行四邊形的面積計算公式）提供三角形紙片，研究這批學生在探索三角形的面積計算公式時的思維過程。

1.原有的轉化方法失效

教師第一次提供給A班32名學生每人一個非等腰三角形紙片，其中有28名學生利用轉化成平行四邊形的經驗，將三角形沿高剪開再拼組，但全部學生都無法將三角形轉化成平行四邊形或長方形。

教師第二次提供給A班每個學生一個非等腰三角形紙片，僅有3名學生能采取如圖1所示的雙側割補法將三角形轉化為長方形，其他學生均轉化失敗，并且沒有學生想到用多個三角形進行拼組。

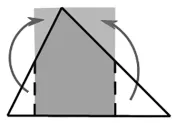
圖1

2.新的轉化方法突兀出現

教師提供給B班35名學生多個不同形狀的三角形，62.56%的學生會利用多個三角形進行圖形的拼組，但教師的教學鋪墊痕跡過重。由于單個三角形轉化的難度，學生在利用兩個相同的三角形拼成一個平行四邊形后，就不再做其他嘗試了。

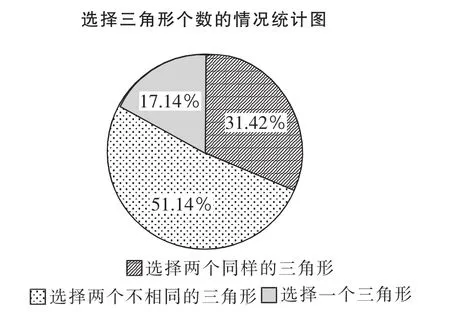
圖2

二、三角形面積教學的策略

1.搭橋牽線，讓“雙拼法”不是空穴來風

教師可以提供給學生等腰和非等腰兩種三角形紙片進行操作，學生借助沿高剪拼的圖形轉化經驗，會出現轉化成功和不成功兩種結果。教師引導學生對比結果，反思原因，從而獲取成功轉化不等腰三角形的經驗：（1）不沿高剪;（2）兩個完全一樣的三角形可以拼成長方形或平行四邊形。

2.借助格子圖,提供合適的形狀素材

對C、D兩個班共65名五年級學生（已經學習了平行四邊形的面積計算公式），教師提供給C班的學習素材如圖3，提供給D班的學習素材如圖4。

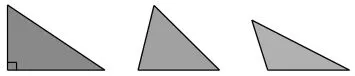
圖3

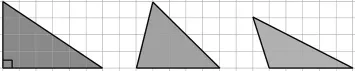
圖4

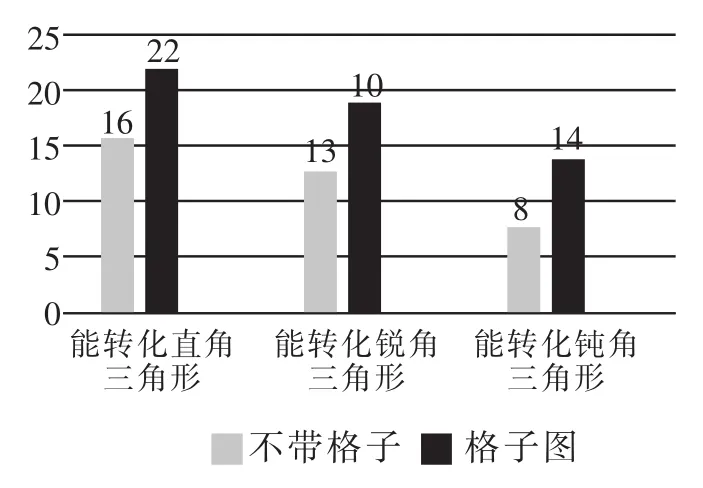
圖5

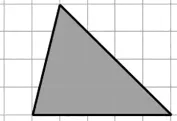
圖6

數據顯示(如圖5）,學生對格子圖上三角形轉化的成功率都高于沒有格子圖的三角形，因此可采用格子圖輔助學生突破單個三角形的轉化難點。學生轉化直角三角形時容易受直角的影響而局限了思路，轉化鈍角三角形時容易受到高在三角形外面的干擾，因此可提供給學生如圖6的學習素材。

3.釜底抽薪，先教學三角形的面積

（1）轉化方法的正遷移

既然平行四邊形的面積教學中轉化方法不能對三角形的面積轉化有所借鑒，平行四邊形的面積計算公式對三角形的面積計算公式又有負遷移，那可以嘗試先教學三角形的面積。

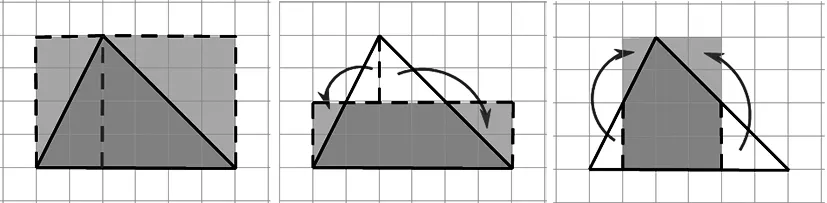
圖7

如圖7，這三種三角形面積的轉化方法都不依賴于平行四邊形的面積計算公式，反過來還可以運用到推導平行四邊形的面積計算公式中來 （如圖8）。

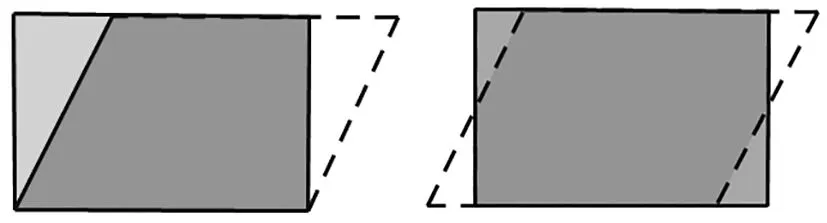
圖8

（2）另辟蹊徑，幾何證明

小學數學中“圖形與幾何”領域的教學偏向于培養學生合情推理的能力，初中階段偏向于培養學生演繹推理的能力，從而造成初小脫節。因此，在小學“圖形與幾何”的教學中，不妨讓學生接觸一些簡單的幾何證明。新加坡的教材在三角形的面積教學中就進行了這種嘗試。

對于格子圖中的直角三角形，可以利用兩個相同的直角三角形拼成一個長方形，計算直角三角形的面積為3×4÷2=6cm2。離開格子圖，借助前面的計算經驗，就可以推導出S直角三角形=ah÷2。

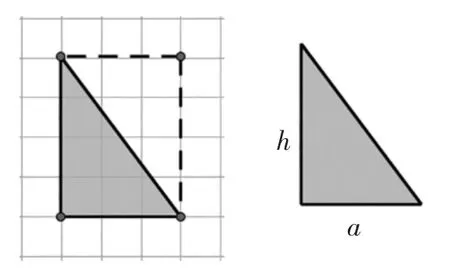
圖9

接著以直角三角形為知識基礎，計算并推導銳角三角形和鈍角三角形的面積計算公式。

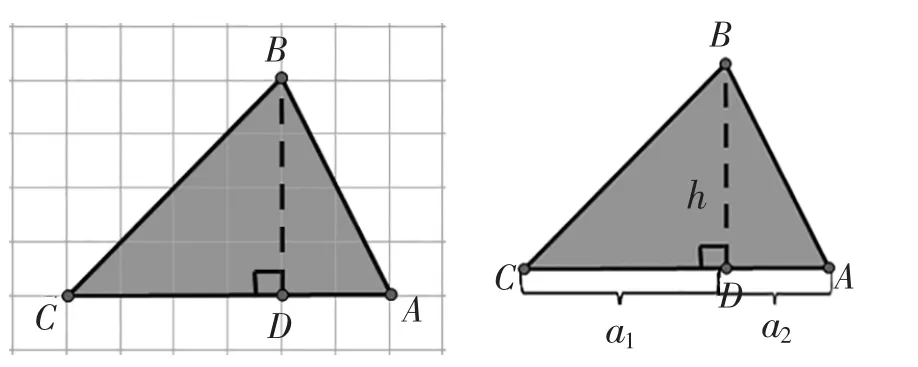
圖10

S△ABC=S△BCD+S△BDA

S=4×4÷2+2×4÷2=12

S=a1×h÷2+a2×h÷2=（a1+a2）×h÷2=AC(底）×h÷2

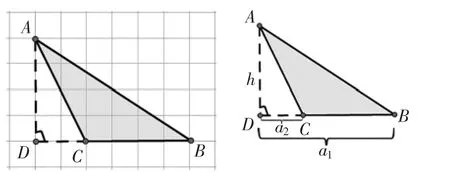
圖11

S△ABC=S△ABD-S△CDA

S=6×4÷2-2×4÷2=12-4=8

S=a1×h÷2-a2×h÷2=（a1-a2）×h÷2=BC(底）×h÷2

雖然這樣的證明方法對學生的思維水平要求比較高，但不妨早一點讓學生接觸，不要求掌握，但試著理解方法。

4.以算促理解，抽象出三角形的面積計算公式

教師將D班中能夠成功轉化銳角三角形的19名學生隨機分為兩組(一組10人，一組9人），提供兩種不同的學習單如圖12。

圖12

A組能推導出面積計算公式的學生比例為70%，而B組僅為22.2%，可見借助具體的數字運算能夠幫助學生更好地理解三角形的底、高與面積之間的關系。

5.用“讀圖讀式”理解多種轉化方法

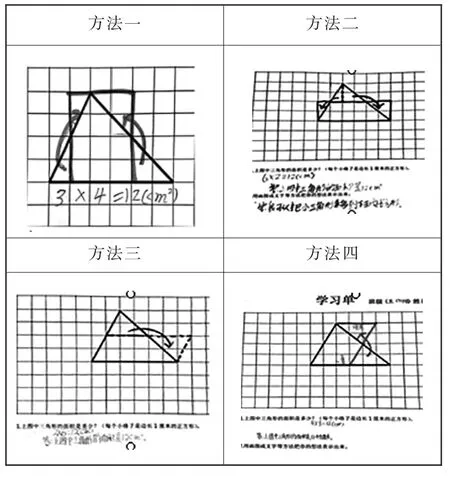
當學生們出現多種方法時，怎么處理？可以參考日本小學數學教材中的方法——“讀式”。

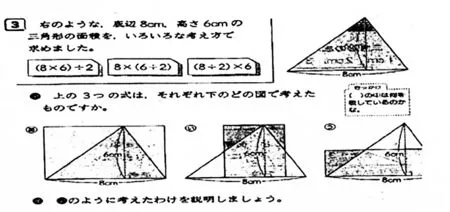
圖中日文翻譯為：“用各種方法求右圖底為8、高為6的三角形的面積， 算式分別為 （8×6）÷2，8×（6÷2），（8÷2）×6， 請說出每道算式對應的是哪幅