思維品質：讓思維更有“格”

江蘇南京市共青團路小學 尹鴻斌

現代教育學認為，數學教學不僅是數學知識的教學，更重要的是數學思維活動的教學，而數學思維能力的高低具體反映在思維品質上，它包括思維的深刻性、靈活性、創造性、廣闊性等品質。因此，學生思維品質的培養既是數學教學的根本目標，又是完成數學教學任務的基本途徑，下面以執教蘇教版數學五年級下冊《解決問題的策略——轉化》的經歷，談談自己的一些體會。

一、從舊知引入新知，培養思維的深刻性

思維的深刻性主要表現為在活動中深入地思考問題，從問題中進行概括并且歸類，然后抓住事物的本質和規律，開展系統的理解活動，能否透過表面現象看本質，這是思維深刻與否的主要表現。

在引入環節，我設計了這樣幾個層次：

（2）圖形中的轉化。出示平行四邊形轉化成長方形的圖：你能說說其中的轉化嗎？

（3）數量關系中的轉化。出示下圖，讓學生說說其中的轉化。

像這樣用“轉化”這一全新的視角，來重新審視學習過的內容，讓學生通過對這些具體的數學材料進行比較、歸納與概括，對具體的計算方法、數量關系和空間圖形進行抽象，從復雜多樣的表面現象中發掘教學內容的本質，溝通知識間的內在聯系，為新知學習進行了鋪墊，達到了溫故知新的目的。進一步地，引導學生透過現象看本質，促進他們思維的深刻性。

二、給學生探究的時間，培養思維的創造性

思維的創造性具體表現為小學生在學習活動中，通過思維活動而得到新穎的思維成果，除了思維的創造性以外，多角度尋求解決問題的方法。

在新授環節，研讀了例題和練習后，我對教材進行了一些處理，設計了這樣的問題 （如下圖），讓學生進行探索。

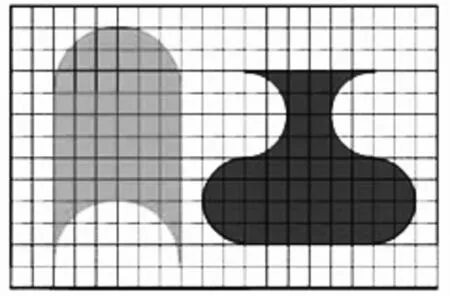
1.下面兩個圖形，哪個面積大一些？你能想辦法比較這兩個圖形的面積嗎？

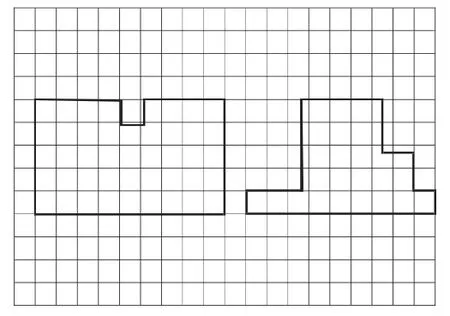
2.下面兩個圖形，哪個周長大一些？你能想辦法比較這兩個圖形的周長嗎？現轉化的具體途徑豐富多彩、精彩紛呈，體現了學生思維品質創造性和廣闊性的統一。

當下的數學教育，教學內容的呈現方式越來越多樣，而解決問題策略的選擇也越來越豐富，在這樣的過程中，要求教師以學定教，順學而教，在課堂上盡可能留給學生充分的時間和空間進行探究，讓學生經歷知識的形成過程，引導學生發現問題，提出問題，并培養解決問題的能力，引導學生多角度進行數學思考。

三、精心設計有效練習，培養思維的靈活性

思維的靈活性是指思維活動的靈活程度，能迅速地從不同的方面、不同的角度來思考問題，并且能用不同的方法來解決問題，它反映了智慧能力的遷移。在教學實踐中，學生往往思維定式，不仔細審題，忽視隱含條件或者解決問題不夠靈活，造成解題錯誤。

練習中，我出示了這樣一題（如下圖），用分數表示其中的涂

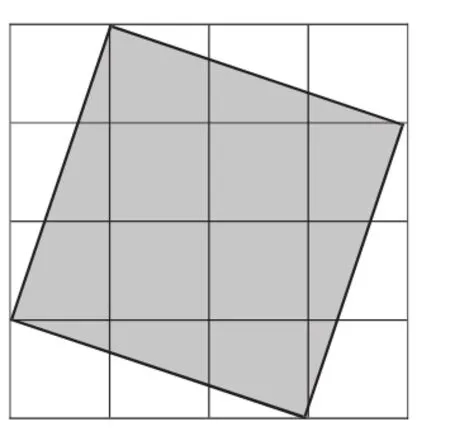
學生在匯報交流的過程中，展示了多種不同的方法。有的在我預料之中，有的在我預料之外。有的同學想出了數格子的方法，有的同學想出的是轉化的方法：通過平移、旋轉，把不規則的圖形變成規則的圖形后，再計算。即使轉化的策略相同，但實色部分。有些思考不嚴謹的同學立即報出答案是，不過并沒有得到大多數同學的響應。這時，就聽到教室里傳來幾聲 “哦—哦—”，于是，我不急著要答案了，讓同桌互相討論討論，為什么答案不是？怎樣才能得到正確答案呢？討論的時候，開始就報答案的同學笑了，說旋轉后只要比一比就能發現，涂色正方形的邊長不是3格，比3格多一點，又不到4格，我看錯了，開始就把邊長當成3格了。邊長無法用整數確定，怎么辦呢？同學們開動腦筋，有的說可以數格子，先把整格的4個數出來，再通過旋轉和平移，就能把剩下的4個直角三角形的涂色部分合并成2個1×3的小長方形再合并，涂色部分有10格，所以答案是；還有的說，把空白部分的4個直角三角形合在一起，它們占6格，那么涂色部分就占10格，也就是

由思維不嚴謹的錯誤引發的思考特別有意義，大家都從中感悟到：要全面地看問題，問題才能得到真正的解決。在解題時，對題目中條件的理解一定要聯系成整體進行理解，想得多了，思維的嚴密性自然就提升了。培養學生思維的靈活性，主要方法就是強調方法最優化和在“大同中找出小異”。

四、及時總結與反思，培養思維的批判性

數學思維的批判性是指，在數學教學中學生對學習過程和結果能主動進行各種方式的檢驗和反思，對已有的數學表述或論證能提出自己的看法，或者提出新的想法和見解。

新授部分的小結中，除了讓學生交流轉化的好處之外，還讓學生體會一下，在轉化過程中要注意的問題。這下學生沉靜下來了，再次回顧學習過程，沉浸到深入思考之中。注意什么呢？要注意在面積轉化的時候，轉化前后的面積不能變；在轉化周長的時候，周長的大小也不能改變。轉化是變形不變質的，因此，同學們在運用轉化策略時一定要關注這一點。很快在練習“用分數表示涂色部分面積”時，學生的學習經歷又一次強化了對這一點的認識。

數學思維品質是一個統一的整體，各個組成部分彼此聯系，密不可分。學生數學思維品質的培養，是在數學教學過程中潛移默化的。無論是在備課還是在教學過程中，教師都應該從學生學的角度出發，有意識地創造條件，有計劃、有目的地強化思維訓練，培養學生良好的數學品質。?