單軸旋轉捷聯慣導系統誤差分析與轉位方案

石瀟竹，胡 杰

（1.空中交通管理系統與技術國家重點實驗室，南京210007；2.中國電子科技集團公司第二十八研究所，南京210007）

0 引言

光纖陀螺是一種無機械轉動的全固態陀螺，被廣泛應用于捷聯慣導系統（SINS）中[1]。光纖陀螺的常值漂移是引起慣導系統導航誤差的主要因素，需要采用相關技術予以補償，旋轉調制技術是SINS中一種常用的誤差自校準方法，可以在不使用外部信息的情況下，通過對慣性測量單元（Inertial Measurement Unit，IMU）周期性轉動以調制IMU的常值誤差，減小對系統精度影響[2]。美國在20世紀70年代開始了此類系統的研究，典型的研究成果有MK39Mod3C、WSN-7B單軸旋轉系統，MK49、WSN-7A雙軸旋轉系統以及ADMII、ADMIII三軸旋轉系統。目前，國外的單軸、雙軸旋轉式慣導系統已經在國內得到應用，三軸旋轉慣導系統也已經完成各項驗證實驗，并有望替代靜電陀螺平臺式慣導系統應用于核潛艇[3-5]。

近年來，國內許多研究機構也展開了旋轉式慣導系統的研究工作[6-9]。文獻[6]分析了單軸旋轉慣導系統自補償基本原理，對影響旋轉調制效果的各項誤差進行了研究。文獻[7]分析了IMU誤差模型和旋轉式捷聯系統誤差傳播方程，設計了單軸正反轉停和雙軸轉位的系統旋轉方案，并進行了相應的數學仿真。文獻[8]提出了一種帶傾斜轉位機構的單軸旋轉調制方案，將IMU放置一定的傾斜角度可以消除轉軸方向上陀螺常值漂移誤差對導航精度的影響，其定位精度與雙軸旋轉慣導系統相當。上述文獻對旋轉調制誤差補償的原理都做了詳細的研究，但對系統的旋轉方式以及工程適用性缺少必要的研究與說明。本文在對IMU誤差調制機理分析基礎上，給出了單軸單向連續旋轉、兩位置正反轉停（大于360°）、四位置正反轉停（小于360°）3種旋轉方式，對不同旋轉方案的誤差調制效果進行了分析與研究，并在單軸旋轉慣導系統上進行了驗證實驗。

1 旋轉調制原理

傳統的SINS中，IMU直接與載體固連，它們之間沒有相對運動。旋轉式SINS中，IMU安裝在轉位機構上，導航計算機控制轉位機構使其做周期性轉動。本文中的IMU由3個光纖陀螺和3個石英撓性加速度計正交安裝組成，旋轉機構具有繞天向軸單軸旋轉功能，IMU固連在旋轉機構上。

定義：s系為旋轉坐標系，b系為載體坐標系，n系為導航坐標系，i系為慣性坐標系，初始時刻s系與b系重合。

單軸旋轉慣導系統中，IMU繞ozb連續旋轉，在t時刻旋轉角速度為Ω，b系相對s系的變換矩陣為：

在旋轉式SINS中，考慮標度因數誤差與安裝誤差，陀螺和加速度計輸出誤差為：

式中，Kg、Ka為陀螺和加速度計的標度因數誤差陣，θg、θa為陀螺和加速度計安裝誤差陣，Bg為陀螺常值漂移，Ba為加速度計常值偏置，δω、δf為陀螺和加速度計隨機誤差。

根據式（1），可以將陀螺和加速度計輸出誤差由旋轉坐標系s轉換到載體坐標系b：

由式（3）可以看出，IMU經過周期性轉動后，x軸和y軸慣性元件的常值誤差，呈現周期性變化，一個積分周期內其誤差為0，z軸誤差沒有變化。

2 旋轉式捷聯慣導系統誤差調制機理分析

考慮標度因數誤差以及安裝誤差，陀螺組合件誤差模型可寫成：

ω，Bg和δω分別表示陀螺一次啟動常值漂移與隨機噪聲誤差。

2.1 標度因數誤差旋轉調制分析

當只考慮標度因數誤差時，陀螺組合件誤差為：

通過分析推導可得：

由式（6）可以看出，經過旋轉調制后標度因數引起的水平方向誤差依然存在直流分量，即單軸旋轉調制對水平方向上的補償作用有限，但在方位軸上引入了大小為KgzΩ的常值漂移。例如：當方位軸陀螺標度因數誤差為1×10－5時，轉位機構16（°）/s的轉速將引入 0.576（°）/h 常值漂移，這對于高精度慣性導航系統是不可容忍的。為了避免轉動引起的標度因數耦合誤差，需要采取正反交替的旋轉方式。

2.2 安裝誤差旋轉調制分析

同理，只考慮安裝誤差時，式（4）可簡化為：

通過分析推導可得：

式中，

由式（8）可以看出，經過旋轉調制后，旋轉軸方向上安裝誤差能夠被調制，水平方向誤差依然存在。

2.3 常值漂移誤差旋轉調制分析

當只考慮常值漂移誤差時，陀螺組合件誤差為：

當轉軸做周期性旋轉時，與轉軸垂直平面上的常值誤差被調制，而轉軸上的陀螺常值誤差沒有補償效果。等效北向陀螺常值漂移和天向陀螺常值漂移決定了系統最終的經度誤差，單軸旋轉調制系統中，水平方向上的陀螺常值漂移經過旋轉調制后誤差被抵消，所以系統能在一定程度上抑制經度誤差的積累，提高了SINS的定位精度。

2.4 隨機漂移誤差旋轉調制分析

陀螺隨機漂移誤差項Cbsδω均值為0，隨機變量經過旋轉調制后依然為隨機變量，因此旋轉調制對隨機漂移沒有調制作用。

加速度計組合件輸出誤差的調制結果與陀螺組合件輸出誤差的調制結果類似，具有相同的結論。

3 旋轉方案設計

3.1 單軸單向連續旋轉

單軸連續旋轉調制系統描述如下：初始時刻s系與b系重合，啟動上電后轉位機構以一定的角加速度加速至角速度為Ω，然后轉位機構一直以該恒定角速度連續旋轉，直到導航系統關機停止工作為止。

3.2 大于360°兩位置正反轉停旋轉

大于360°兩位置正反轉停旋轉方案如圖1所示，轉動方案描述如下。

次序1：IMU從位置A點出發逆時針轉180°到達位置B點，停止時間Ts；

次序2：IMU從位置B點出發順時針轉180°到達位置A點，停止時間Ts；

次序3：IMU從位置A點出發順時針轉180°到達位置B點，停止時間Ts；

次序4：IMU從位置B點出發逆時針轉180°到達位置A點，停止時間Ts。

然后按照次序1～次序4的順序循環運動，不同位置處停留5min。

3.3 小于360°四位置正反轉停旋轉

小于360°四位置正反轉停旋轉方案如圖2所示，轉動方案描述如下。次序1：IMU從位置A點逆時針轉動180°到達位置C點，停止時間Ts；

次序2：IMU從位置C點逆時針轉動90°到達位置D點，停止時間Ts；

次序3：IMU從位置D點順時針轉動180°到達位置B點，停止時間Ts；

次序4：IMU從位置B點順時針轉動90°到達位置A點，停止時間Ts；

然后按照次序1～次序4的順序循環運動，不同位置處停留5min。

4 仿真研究

4.1 慣性器件參數設置

假設3個陀螺的常值漂移均為0.01（°）/h，隨機游走系數為0.001（°）/h，標度因數誤差為 1×10－5，陀螺組件的6個安裝誤差角為10″；3個加速度計的偏置均為100μg，隨機白噪聲標準差為200μg，標度因數誤差為1×10－5，加速度計組件的6個安裝誤差角為10″；轉位機構測角精度為5″。

4.2 載體運動參數設置

初始經度為 106.6906°，緯度為 26.5019°；系統模擬搖擺運動，姿態角變化規律分別為：俯仰角，橫搖角，航向角

假設初始航向角誤差為1′，初始俯仰角誤差和橫搖角誤差均為15″，旋轉機構測角誤差為5″，陀螺和加速度計采樣間隔時間為5ms，由于連續旋轉方式不具有工程應用價值，這里僅對以下3種方案進行仿真，仿真時間設置為72h。

1）沒有旋轉；

2）大于 360°兩位置正反轉停旋轉，轉速為16（°）/s，每個位置停留時間為 5min；

3）小于 360°四位置正反轉停旋轉，轉速為16（°）/s，每個位置停留時間為 5min。

圖3給出了3種轉位方式下的導航定位誤差曲線。

由圖3可以看出，兩位置正反轉停方案與四位置正反轉停方案72h的定位精度相當，分別為18.37nmile和18.36nmile。而非旋轉式 SINS中，同樣的慣性器件誤差條件下，其72h的定位誤差為55.52nmile，這充分體現了旋轉調制的作用，同時也說明了四位置轉停方案與兩位置轉停方案具有同樣的抑制導航誤差性能。

5 實驗及分析

利用實驗室三軸轉臺、車載實驗系統和自行研制的單軸旋轉SINS進行驗證實驗，其中IMU由3個光纖陀螺與3個石英撓性加速度計組成。轉臺實驗環境和車載實驗環境分別如圖4和圖5所示，單軸旋轉SINS的主要技術參數如表1所示。

在實驗室環境下，轉位機構轉位方式采用四位置轉停方案。四位置轉停方案中采用的轉位機構不需要導電滑環，因此具有更高的可靠性，產品上電后轉位機構初始化使得載體坐標系b與旋轉坐標系s重合。圖6詳細描述了慣導系統實驗過程中各個時間段的工作狀態，前3min進行粗對準，采用的是慣性系解析法[10]；然后進行精對準，精對準時間為20min，精對準結束后，轉入到純慣性導航工作模式。轉臺實驗和車載實驗分別進行了兩組驗證實驗，其中一組實驗轉位機構停止旋轉；另一組實驗啟動轉位機構，進行誤差調制。

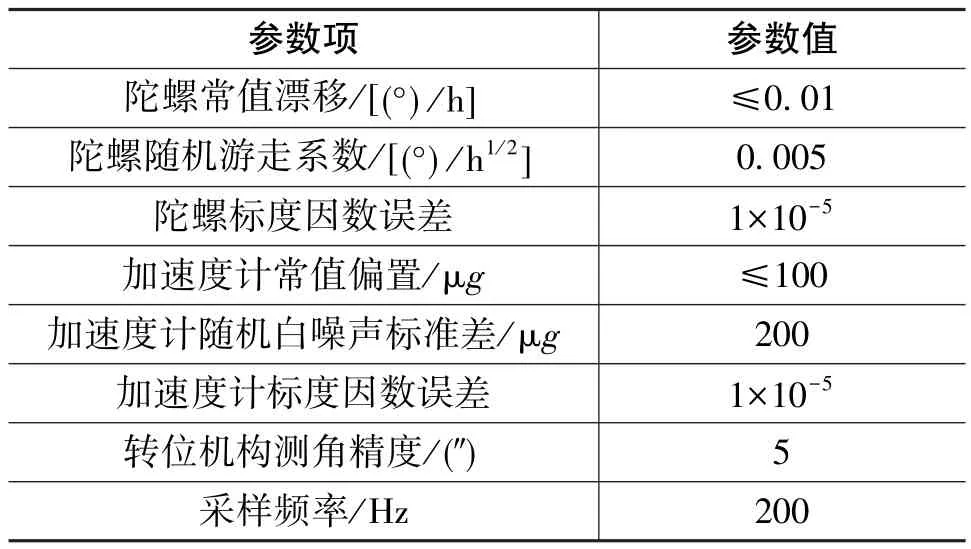
表1 單軸旋轉捷聯慣導技術參數Table 1 Specifications of the single-axis rotary SINS

圖7為轉臺實驗誤差對比曲線，由圖7可知，當系統IMU不進行旋轉時，5h導航結束后的定位誤差為1.98nmile。當IMU進行四位置轉停旋轉后，其5h導航結束后的定位誤差為0.51nmile，說明了單軸旋轉調制能夠抵消IMU誤差對系統精度的影響，提高了SINS的定位精度。

圖8是某次車載實驗路線圖，在起始點先進行初始對準實驗，對準結束后啟動車輛開始實驗。沿著路線以10km/h的車速到達某處調頭繼續行進到實驗結束，驗證實驗共進行了5h。

由圖9可知，系統不進行旋轉調制導航時，5h內位置誤差最大為2.2nmile。當采用四位置單軸旋轉調制方案時，5h系統定位誤差最大為0.81nmile，系統最終定位精度得到了很大的提高。

結合轉臺搖擺實驗和車載環境動態實驗定位誤差結果可知：水平方向陀螺誤差對定位精度的影響基本被調制，系統實驗結果滿足初始設計指標，可以為單軸旋轉SINS的研制提供理論與實踐指導。

6 結論

本文對旋轉式SINS誤差特性進行了分析，給出了旋轉調制對陀螺標度因數誤差、安裝誤差、常值漂移和隨機誤差的調制作用。單軸旋轉調制能將與轉軸垂直方向上的慣性器件的常值誤差調制成周期性分量，通過積分運算，可以消除其對導航定位精度的影響。轉軸方向上的標度因數誤差會與旋轉角速度相耦合，這樣會進一步放大其對導航定位精度的影響，因此在工程應用中需要采取正反旋轉的方案，以抵消該項誤差。旋轉調制對安裝誤差以及隨機噪聲誤差的調制作用很小，高精度導航系統前期轉臺標定時應盡可能減小該項誤差。

給出了單軸旋轉SINS的3種常用轉位方式，在數學仿真環境下對其中兩種轉位進行了仿真驗證，指出兩位置與四位置具有同樣的旋轉調制功能，但是四位置轉停方式不需要滑環，工程應用中具有更高的可靠性。利用三軸搖擺轉臺、車載實驗系統以及單軸旋轉SINS進行了靜態和動態驗證實驗，結果能夠滿足系統初始設計指標，具有工程參考價值。