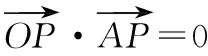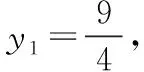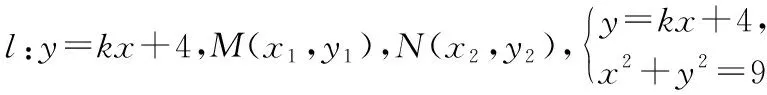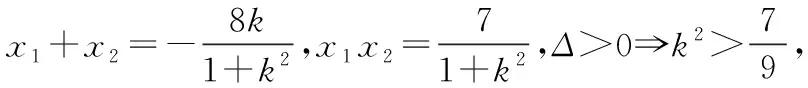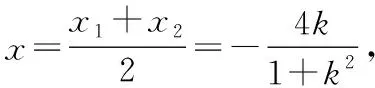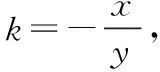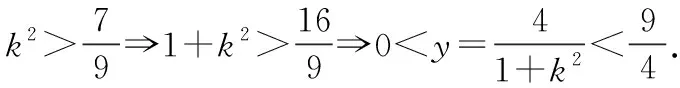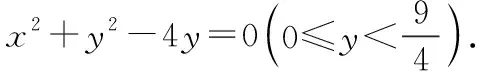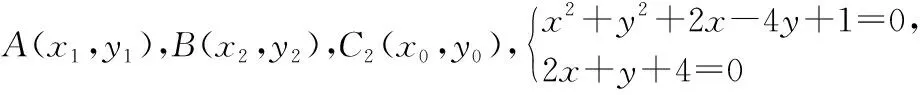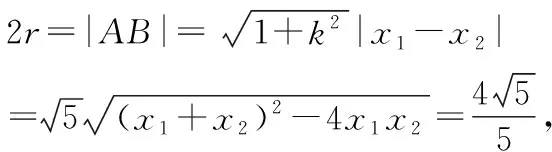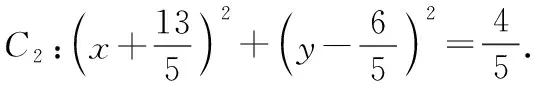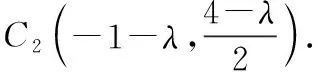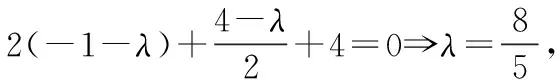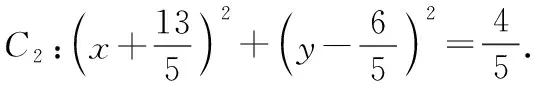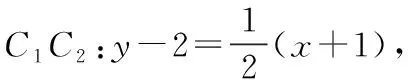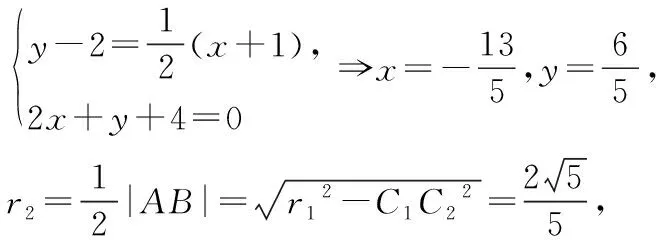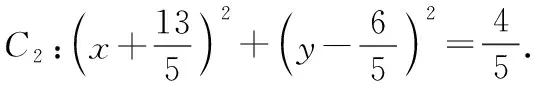“直線與圓的位置關系”的教學思考

◎蘇仕剛

(安徽省肥東第一中學，安徽　合肥　231600)

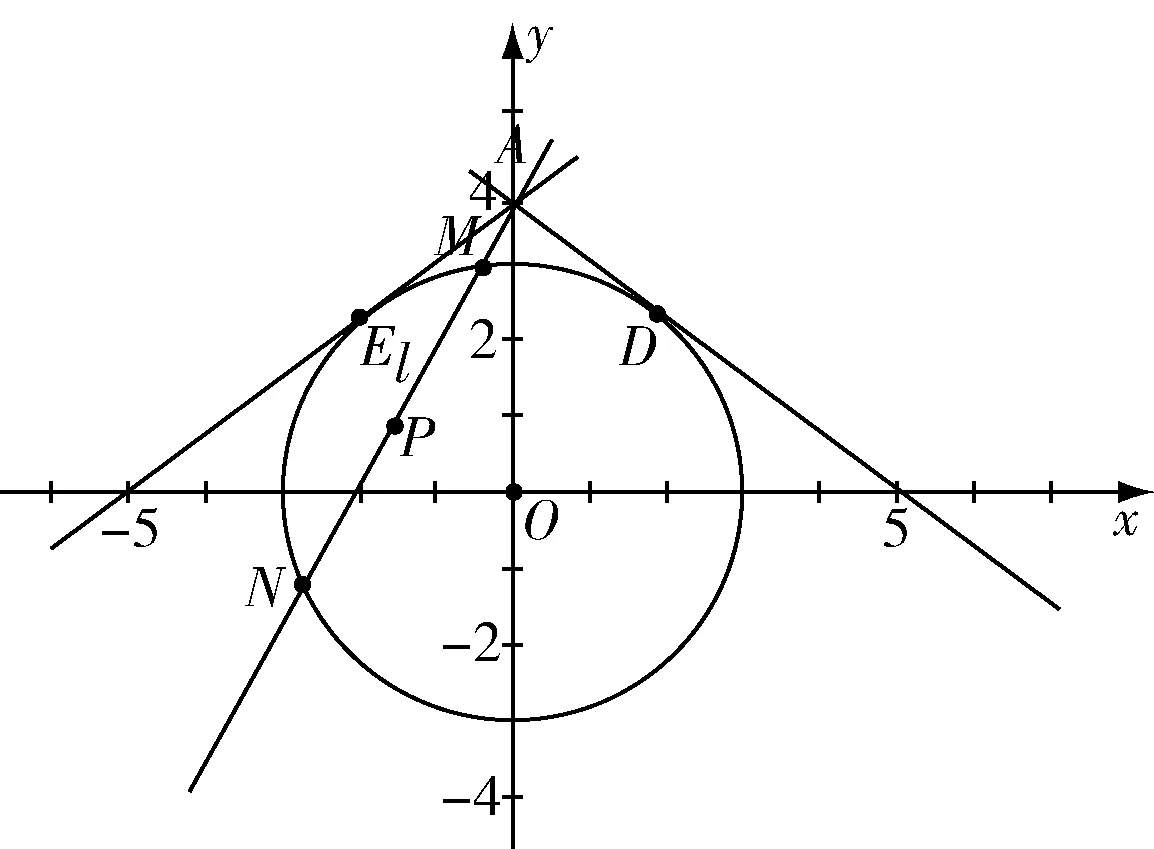
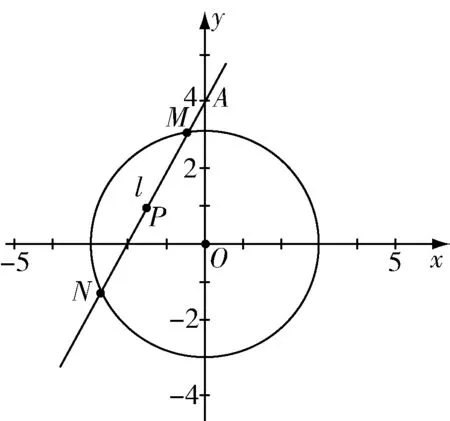
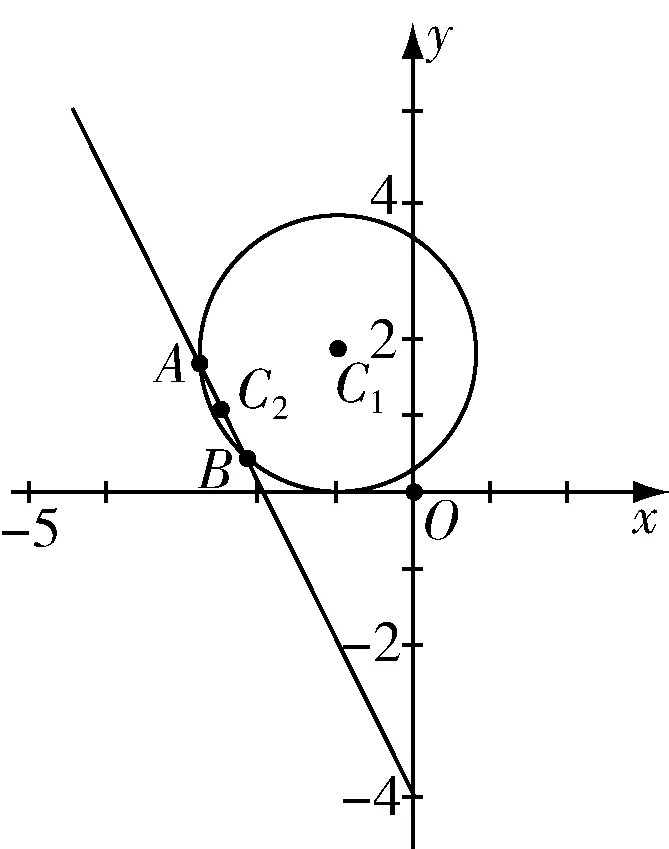
由平面幾何知識可知，直線與圓有三種位置關系：(1)直線與圓相交，有兩個公共點；(2)直線與圓相切，只有一個公共點；(3)直線與圓相離，沒有公共點.判斷直線與圓的位置關系的方法有：一種是幾何觀點，即通過計算圓心到直線的距離d與半徑r的大小來判斷，若d>r，則相離；若d=r，則相切；若d

淡化方程觀點的方法，這與教材的精神也不符.教材在內容的設置上也體現出要我們認真對待用方程的觀點來研究這部分相關內容的，如，人教版必修2的137頁，首先就用這樣的思考：“現在如何用直線的方程與圓的方程判斷它們之間的位置關系？”來引入用方程的觀點來探究直線與圓之間的位置關系，也容易讓學生在回顧第三章已經運用直線的方程研究了直線之間的位置關系，以及直線與直線間位置關系的簡單運用，很快就過渡到本節也可以采用這種方法來研究直線與圓的位置關系及其相關的一些問題，從而把這種方法推廣為一種研究直線與曲線之間關系的通法.此外教材在本節138頁的例1給出了兩種解法，首先就給出了從直線與圓的方程出發，通過它們的方程組成的方程組的實數解的情況，來判斷直線與圓之間的位置關系，并把這種解法作為該例題的方法一，從而也突出了這種思維方法的重要性，所以我們在教學的過程中理應重視它.

也有的觀點認為在這里運用方程的觀點來聯立方程組，有時方程處理起來又非常麻煩，浪費了教學時間，不如用幾何的觀點簡單快捷，學生易操作.特別是高中數學課堂教學時教師們普遍感到平時教學的時間很緊，在這里再來花時間強調乃至拓展強化這種方程的觀點，總覺得有點不值.這種觀點我認為是教學目光短淺的一種表現，若把它放到整個教學體系上去看待本節知識，認識這種方程的觀點，在這里花點時間來幫助學生對這種解題理念的形成，你就會覺得很值很有必要了.在解析幾何中，直線與圓的位置關系是很重要的一個知識，不僅可以對學生的數學思維有一個很好的鍛煉和提升，還將“曲線與方程聯系起來，實現形與數的統一”的這種重要的解析幾何的數學思想傳輸給學生，也為學生后續學習直線與圓錐曲線的位置關系奠定良好的基礎.所以除了講好教材中直接體現這種方程觀點的知識內容外，還應引入一些問題來幫助學生形成這種數學思想，并會用這種思想方法來獨立地分析問題解決問題.

問題一已知圓O的方程：x2+y2=9，求過點A(0，4)所作的圓的弦中點P的軌跡方程？

方法一如圖所示，設弦MN中點P(x，y)，

?x2+y(y-4)=0?x2+y2-4y=0.

?

以方程?的解為坐標的點都在弦中點P的軌跡上嗎？∵A點在圓外，∴過A點所作的直線與圓O不一定相交，故只能是方程?的部分解為坐標的點所對應的軌跡.現在過A點作圓O的切線，切點分別是D，E，并設D(x1，y1)，E(x2，y2)，∴直線AD的方程：xx1+yy1=r2=9.

①

②

問題二已知直線l：2x+y+4=0，圓C1：x2+y2-4y+2x+1=0.當l與圓C1交于A，B兩點，求過A，B的圓C2的面積最小時圓C2的方程.

分析以|AB|為直徑的圓的面積最小.

方法二以AB為直徑的圓方程

(x-x1)(x-x2)+(y-y1)(y-y2)=0

?x2+y2-(x1+x2)x+x1x2-(y1+y2)y+y1y2=0.

?

其中y1y2=4x1x2+8(x1+x2)+16，

y1+y2=-2(x1+x2)-8.

代入方程?可得圓C2的方程：

方法三設x2+y2-4y+2x+1+λ(2x+y+4)=0

∵C2在直線l上，

方法四∵AB是圓C1的弦，且C2是AB的中點，

∴直線C1C2垂直平分AB，

通過上述問題的引入與講解，不僅能引導學生在學習解析幾何時要有“方程觀點”的意識，還能讓學生初步形成用代數的方法解決解析幾何問題的能力，也為將來學生進一步學習選修1-1、選修2-1中的“圓錐曲線與方程”打下堅實的數學基礎.

所謂“方程的觀點”就是解析幾何中坐標法這一重要數學思想的體現.我們在平面解析幾何初步的教學中，一定要讓學生真正地經歷這樣的學習過程：通過建立平面直角坐標系，將所研究的幾何問題代數化，用代數的語言描述幾何要素及其關系，即建立曲線與方程的等價性.再通過處理代數問題，分析代數結果的幾何意義，最終解決幾何問題.這種教學思想理念應貫穿平面解析幾何的教學始終，一定不能偏離這個主線，否則對學生數學能力(數形結合的思想方法)的形成就會產生很不利的影響.