再探究柯西不等式在2017年高考數學中的應用

◎王立榮

(陜西省商洛市商州區大荊中學，陜西　商洛　726001)

柯西不等式是高中數學中的一個重要不等式，它在中學數學中有多方面的應用.近幾年柯西不等式在全國各地高考試題中的應用屢見不鮮.2017年全國及各地高考數學試題中，柯西不等式又體現了其應用的廣泛性.下面略舉幾例，供大家參考.

一、在不等式證明中的應用

例1(2017年全國Ⅱ理23)已知a>0，b>0，a3+b3=2.證明(a+b)(a5+b5)≥4.

證明由二元柯西不等式，得

∴(a+b)(a5+b5)≥4.

例2(2017年江蘇21D)已知a，b，c，d均為實數，且a2+b2=4，c2+d2=16.證明ac+bd≤8.

證明由二元柯西不等式，得

(a2+b2)(c2+d2)≥(ac+bd)2，4×16≥(ac+bd)2，

∴(ac+bd)2≤64，∴ac+bd≤8.

二、在向量中的應用

解如圖所示，建立以B點為原點的平面直角坐標系，則B(0，0)，A(0，1)，C(2，0)，D(2，1).

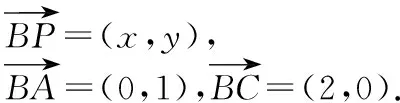
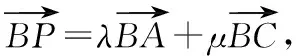
∴(x，y)=λ(0，1)+μ(2，0)=(2μ，λ)，

∴x=2μ，y=λ.

∵已知圓與BD相切，設切點為E，連接CE，則CE⊥BD，且CE是圓的半徑.

∴(2μ+2λ-4)2≤4，∴2μ+2λ-4≤2，

∴λ+μ≤3，∴λ+μ的最大值是3.

∴此題答案為A.

三、在最值中的應用

例4(2017年北京文11)已知x≥0，y≥0，且x+y=1，則x2+y2的取值范圍是________.

解由柯西不等式，得

(12+12)(x2+y2)≥(1·x+1·y)2=(x+y)2=1，

四、在解析幾何中的應用

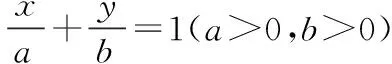
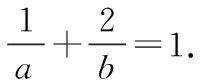
∵a>0，b>0，由柯西不等式，得

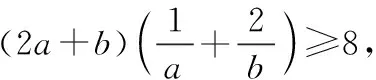
即(2a+b)×1≥8,∴(2a+b)≥8,

∴2a+b的最小值是8.

五、在三角函數中的應用

例6(2017年全國Ⅱ文13)函數f(x)=2cosx+sinx的最大值為________.

解由柯西不等式，得

(22+12)(cos2x+sin2x)≥(2cosx+sinx)2,

即5≥(2cosx+sinx)2,

總之，柯西不等式的廣泛應用在多年的高考試題中均有體現，尤其在2017年全國和地方高考試卷中都有柯西不等式應用的影子.因此，在高三數學復習中，柯西不等式應引起足夠重視.當然，在應用柯西不等式時，柯西不等式形式的靈活構造這一數學構造思想顯得尤為重要.