地方應用型本科院校高等數學教學改革研究
——以函數的連續性為例

◎張府柱　杜　云　張文林

(六盤水師范學院，貴州　六盤水　553001)

地方新升本院校定位為應用型本科院校時，這類學校在教育教學上基本模仿研究型大學辦學.在教學過程中產生了諸多問題，例如，隨著實踐學分的增加，給理論教學在學時分配上提出了挑戰，以高等數學為例，升本前專科生每學期18周的上課時間，周學時達到6節，升本后的本科生每學期16周的理論授課時間，2周的實踐教學，高等數學的周學時一般是4學時，從108節減少到64節，反映出來的情況是理論掌握不好，計算能力薄弱，應用能力較差，與應用型的定位不相匹配.所以，在教學方法上要進行相應的改變.下面將以函數的連續性教學為例，介紹一下我們的做法，以供同行參考交流.

用極限討論函數的分析性質，連續性是第一個.

同濟大學數學系編寫的高等數學第七版教材，是通過自然界中的一些連續的現象，如氣溫的變化、河水的流動、植物的生長等給學生一些連續的映象，然后分析變量的增量引入點連續的概念，然后介紹右、左連續的概念，很多教材基本上以它為藍本進行編寫.而對地方新升本的應用型本科學生來說，還是不能適應，依然不知道連續性是什么？連續性有什么用處？

下面介紹一下我們的處理方式.

一、由觀察幾個函數圖形，在學生的腦海中產生直觀的函數在一點連續的映象

提問：根據你們對“連續”的理解，說說下面幾條曲線的連續性.

學生都能說出圖1、圖2和圖3的曲線都不連續，圖4的曲線連續.其實學生對連續的直觀映象是正確無誤的.

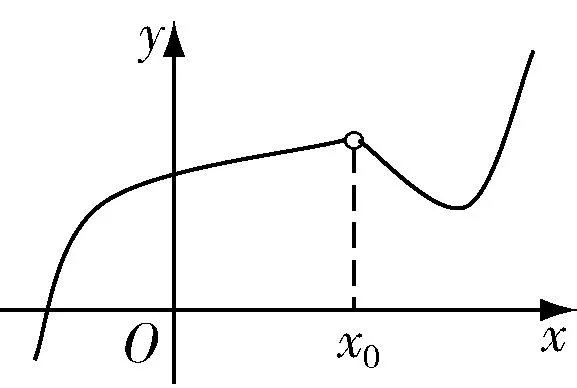
圖1　不連續

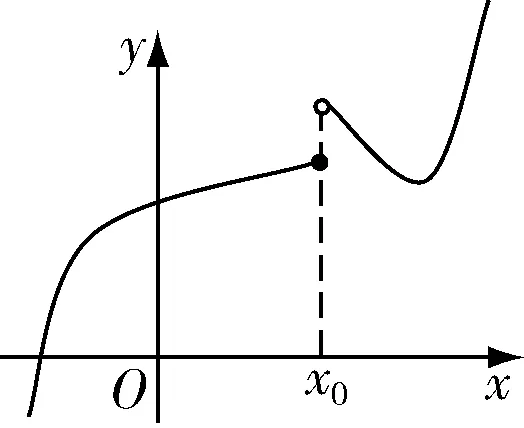
圖2　左連續

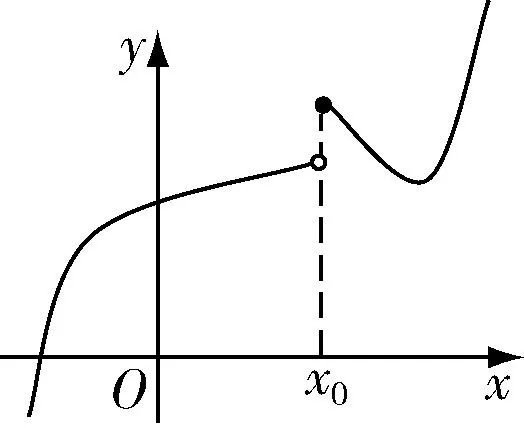
圖3　右連續

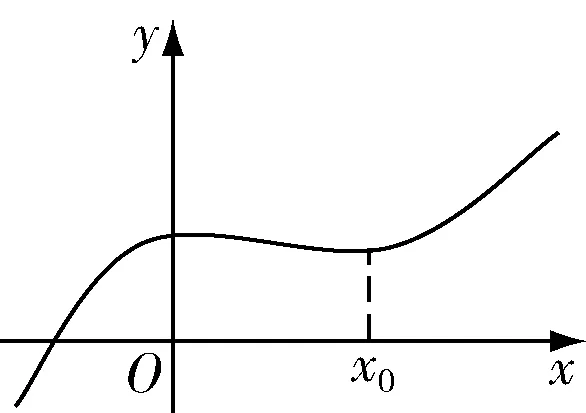
圖4　連續

提問：前三條曲線不連續，它們之間有什么區別？

第一條曲線在x0是斷開的，第二條曲線在x0處也是斷開的，但是，點(x0，f(x0))和左邊的曲線是連在一起的，教師引導學生這就是左連續.這時，學生就能正確地回答圖3的曲線是右連續，圖4是連續的.

從這一問一答中，學生基本上對函數的連續性有了正確的直觀映象.

二、用語言來描述函數在一點的左連續、右連續和連續

先這樣啟發學生，設想一個人沿著曲線行走，不連續的曲線從左端能走到右端嗎？左連續、右連續和連續情況如何？學生基本上能回答：不連續的曲線從左端不能走到右端；左連續的曲線可以從左邊到達(x0，f(x0))點，右連續的曲線可以從右邊到達(x0，f(x0))點，連續的曲線可以從左端走到右端.通過這樣的設想，在啟發學生回憶一下函數極限，函數的連續性就與極限過程聯系起來，于是得到了下面的一些關系.

左連續?點(x0，f(x0))左邊的圖形連接起來?

右連續?點(x0，f(x0))把右邊的圖形連接起來?

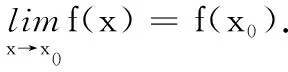
到了這里，函數的連續性已經在學生的腦海里基本建立起來了，而且三者之間的關系也被揭示出來了，連續?既左連續又右連續.上述直觀定義還缺少嚴格性，我們需要附加一些條件才能得到嚴格的定義.

三、函數在一點的連續性

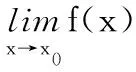
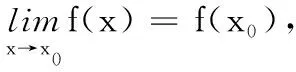
那么就稱函數y=f(x)在點x0連續.

其本質就是極限值等于函數值，于是我們得到下面的等價定義.

定義1′函數y=f(x)在點x0連續??ε>0，?δ>0，當|x-x0|<δ時，有|f(x)-f(x0)|<ε.

提醒學生注意這個定義與極限的ε-δ定義的區別與聯系，并類比函數極限的幾何意義寫出函數連續性的幾何意義.

若記Δx=x-x0，稱為自變量x在點x0處的改變量(或增量)，函數對應的增量Δy=f(x0+Δx)-f(x0)，則有下面的等價定義.

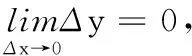
這個定義可以很好地解釋動物和植物的生長是連續地變化著的，因為當自變量時間趨于無窮小時，因變量高度也趨于無窮小，所以我們看不到它們在往高處生長.

類似地，我們可以定義單側連續以及單側連續與連續的關系.

四、函數在一點的單側連續性

設函數y=f(x)在點x0的某一鄰域內有定義.

單側連續性也同樣具有連續類似的等價定義，可以由學生作為練習.

定理1連續?既左連續又右連續.

五、總　結

以上的教學過程，打破了傳統的先給出一系列的定義，再舉若干例子，最后到若干定理的教學過程.它首先通過觀察圖形，給學生連續與不連續的直觀認識，通過教師不斷啟發，用自己的語言對函數的連續性進行描述，通過一個設想和前面學習的極限過程對比，得出了用極限來給連續性下定義.再由極限的變形得出函數連續性的其他形式的定義.從教學效果來看，學生對函數在一個點的連續性有了深刻的理解，對下一步學習函數的間斷點的區間連續打下了堅實基礎.

地方應用型本科院校的教學目標與研究型大學的教學目標不同，對于一個數學對象，前者需要掌握是什么?了解為什么?重點是怎么做(應用)?后者遵循一種不完全的公理化線索，不但要掌握是什么，而且通過嚴格的邏輯推導為什么，了解怎么辦(應用).所以，根據不同的教學目標，選擇不同的教學方法，這才是真正的因材施教.