一種基于CLEAN的稀疏陣列波達方向估計方法

楊　剛　袁子喬　杜　力

(西安電子工程研究所　西安　710100)

0　引言

在雷達和通信系統中，陣列天線應用極其廣泛。到目前為止，均勻間隔分布的天線是最簡單且應用最廣的陣列天線之一。然而均勻間隔分布的天線陣列存在出現柵瓣的可能性，為避免柵瓣的出現，通常要求天線陣列的間距不大于波長的一半。因此，如果想要獲得較高的角度分辨力就需要很多的陣元，這不僅會增加天線的成本，而且產生的大量數據也會增加數字信號處理系統的負擔。

對均勻分布的陣列進行稀疏化處理，也就是從均勻陣列中隨機去掉一些陣元，使得陣元不再規則排列得到稀疏陣列。稀疏陣列能夠有效的抑制柵瓣的出現，并且能夠提高角度分辨力，但它的峰值旁瓣和均值旁瓣都比較高，有出現假目標的可能性。

波達方向(Direction of Arrival， DOA)估計一直是陣列信號處理領域的熱點之一，精確的DOA估計對后續處理至關重要。當前對DOA估計算法的研究主要集中在MUSIC[1]和ESPRIT[1-2]兩種優秀的算法上[3]。雖然MUSIC算法具有很好的分辨力，但該算法需要在所有可能的角度進行譜峰搜索，運算量極大，而且測角精度和所選的搜索角度的間隔相關。Root-MUSIC[4]是在MUSIC的基礎上提出的，其無需進行譜峰搜索，直接得到閉式解。不過，Root-MUSIC算法的策略是求方程的根，隨著陣元數的增加，方程求根的時間會急劇增加，所以在陣元數較多的場合Root-MUSIC會增加時間上的負擔。

為了避免高旁瓣可能出現假目標的問題，本文提出了一種基于CLEAN的測角算法，并通過與Root-MUSIC算法的仿真實驗對比說明了該方法的有效性。為表述方便，本文用一維陣列來進行描述，但本文所提算法同樣適用于二維陣列。

1　算法描述

1.1　陣列天線接收信號模型[5]

對于一個由N個陣元組成的一維線性陣列天線，在其中隨機去除一些陣元可以得到稀疏陣列。為描述方便，用一個包含N個元素的一維數組Arr表示稀疏陣列，其中，去除的陣元對應的元素為0，保留的陣元對應的元素為1。假定陣元間距為d，有p個入射信號，方向分別為θi(i=1,…p)，各陣元接收到的噪聲為零均值高斯白噪聲。則接收到得信號可以表示為：

X=(AS+N)·Arr

(1)

式中，X為采樣數據，S為信號矢量，N為噪聲矢量，A為導向矢量矩陣，具體為：

A=[a(θ1)a(θ2) …a(θp)]

(2)

式中，a(θi)為第i個信號的導向矢量，具體為：

a(θi)=[1,ejkdsinθi, …,ejk(N-1)dsinθi]T

(3)

式中k=2π/λ，d為陣元間距。

1.2　FFT多波束形成

在做FFT形成多波束之前，需要判斷目標的個數。目標個數的準確確定對DOA估計十分重要，如果目標數選擇過大，則會出現虛假目標，如果選擇過小，則會漏掉目標。本算法中采用最小描述長度(MDL)準則來計算目標個數。

在形成波束時，對各陣元的采樣數據進行加權求和，得到陣列輸出

y=WHX=WH{(AS+N)·Arr}

(4)

其中，W=[w1,w2,…wN]T為各陣元對應的權值。當W=a(θi)時，波束將指向θi方向。

此時，

(5)

若進行量化，

(6)

則式(5)就是X(t)的DFT表達式，實際中，經常用FFT來實現。所以對陣列得到的采樣值進行M點FFT，就可以得到M個接收波束數據，各波束號與對應的波束指向角度的關系如式(6)所示。

對于快拍數為L的數據，通過對得到的波束數據進行模的平方累加，最終數據為：

(7)

1.3　等信號和差測角法[6]

由FFT形成的兩個波束之間的差波束與和波束之比與目標同等信號軸的偏差近似成正比，類似的，先對兩波束的幅度求平方，然后再求和波束Σ和差波束Δ，Δ/Σ仍然與目標偏離等信號軸的偏差成正比。因此，利用式(7)求得各波束的累加結果后，P中相鄰兩波束的差波束與和波束之比與目標偏離等信號軸為線性關系。找出P中最大值對應的波束號p1，以及該目標對應的次大值的波束號p2。

(8)

然后，利用以下公式得到該目標對應的“精確波束號”pt。

(9)

其中，k為陣列對應的比幅測角斜率，與具體陣列相關，利用式(5)，求得多波束響應y，然后取P=|y|2，將p1和p2選為0…M-1中任意相鄰的值，再將pt取為p1和p2之間的值，利用式(9)可求出k。sign為符號位，取值如下：

(10)

利用式(6)可得該目標對應的角度為：

(11)

1.4　CLEAN算法的應用

由于稀疏陣列的旁瓣比較高，產生的假目標在P中對應的值很可能大于真實的弱目標在P中對應的值，所以P中的極大值點有可能對應的是假目標。因此，當MDL求得有T個目標時，在P中取最大的T個極大值點認為是目標是不正確的。

為了抑制假目標的影響，應用CLEAN的思想，在每得到一個目標后，在計算結果P中清除該目標的響應。精確的做法應該是在每個快拍清除該目標帶來的影響，但這樣做算法復雜度會很大，在實時性要求高的場合達不到系統要求。通過仿真實驗，我們發現，把所有快拍的計算結果(即P)看作是一個快拍的計算結果，僅作一次清除操作得到的結果與每個快拍做一次清除操作得到的結果十分接近。假設目標Tm在Pm-1中對應最大波束號為zm，由式(11)求得的角度為θm，其對應的幅度為：

(12)

在Pm-1清除目標Tm的響應后，得到：

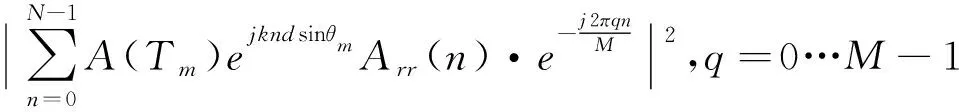
(13)

利用遞歸的思想，在清除操作后的結果中繼續找最大值點，繼續清除，直至計算完T個目標時停止。

2　仿真實驗與結果

不是一般性，我們選用了稀疏陣列Arr=[1 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1 1 1 1 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 0 1 1 1 0 1 1 0 0 0 1 1 1]，陣元間距為0.5909λ，所有涉及蒙特卡羅實驗的次數(MC)都是200。實驗中所加噪聲均為加性高斯白噪聲，快拍數為64，所有FFT的點數均為128點，除了實驗一外，其他實驗都用2個目標并且加了泰勒窗。在后文中，FAC代表本文提出的算法，RM代表Root-MUSIC算法。對比方法主要是平均均方誤差(RMSE)，2個目標對應的計算公式為：

(14)

實驗一：本論文實驗中采用的稀疏陣列有效陣元數(Arr中為1的個數)為28，將此稀疏陣的方向圖與陣元間距為0.5λ的28個均勻線陣的方向圖進行對比，結果如圖1所示。可以看出，相同(有效)陣元情況下，稀疏陣(對應圖中紅色)可以獲得更窄的主瓣，但均值旁瓣和峰值旁瓣都比較高。

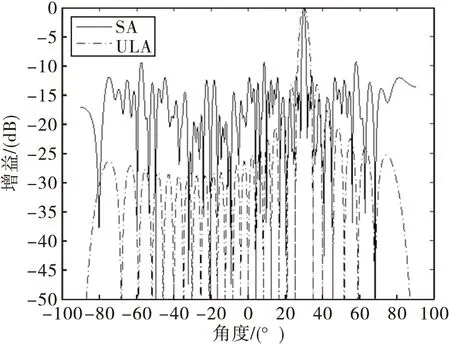
圖1　均勻陣與稀疏陣方向圖對比

實驗二：為對比FAC與Root-MUSIC的時間復雜度，選取陣元數為6至60的一維均勻線陣，兩個目標的入射方向分別為20°和40°，SNR為都是20dB。實驗結果如圖2所示。由圖2可以看出在陣元數小于20時，RM耗時較少，在陣元數大于等于20時，FAC耗時較少；同時可以看出，當陣元數增加時，RM的時間快速增加，但FAC的時間增加十分緩慢。可以說明FAC方法的時間對陣元數不敏感，耗時總是很少。

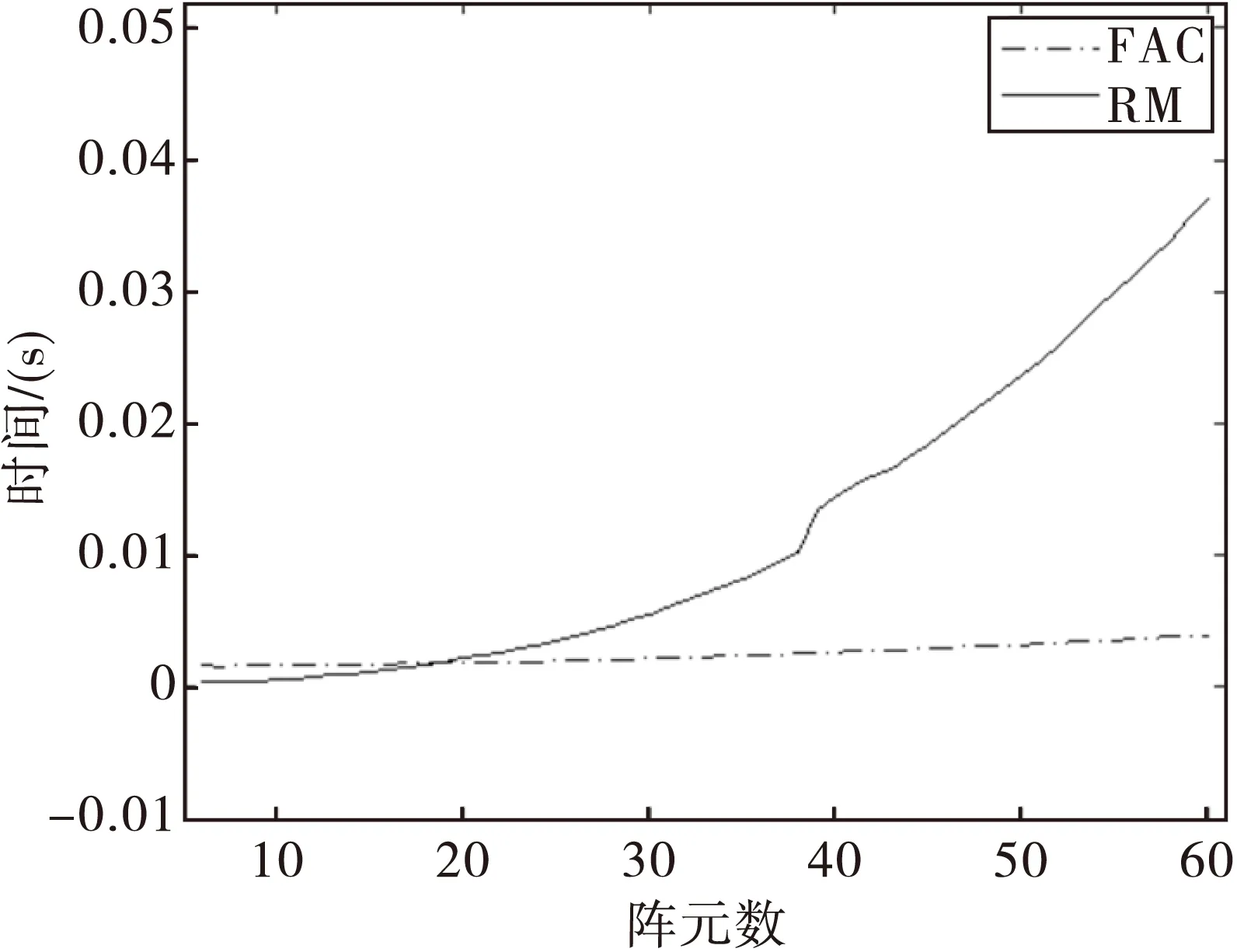
圖2　FAC與RM的時間對比

實驗三：為驗證當強目標旁瓣的響應大于弱目標的響應情況下FAC的性能，本實驗中，兩目標的SNR分別選為20dB和40dB，入射角度分別為10°和30°。利用式(7)計算的響應圖見圖3(a)，可以看出最大值點對應的是30°的目標，而10°目標對應的響應并不是一個極值點，因為30°目標帶來的旁瓣響應超過了10°目標對應的響應。30°目標對應的響應(也即式(13)中第二項)如圖3(b)所示，在圖3(a)中去除圖3(b)得到圖3(c)，可以看出30°目標對應的響應被很好地清除了，10°目標對應的峰值顯現了。FAC求得的結果為：10.031°和29.999°，RM計算的結果為：10.044°和29.946°。通過本實驗說明，FAC在強目標旁瓣響應大于弱目標響應的情況依然能夠精確的估計出所有目標的入射角度。

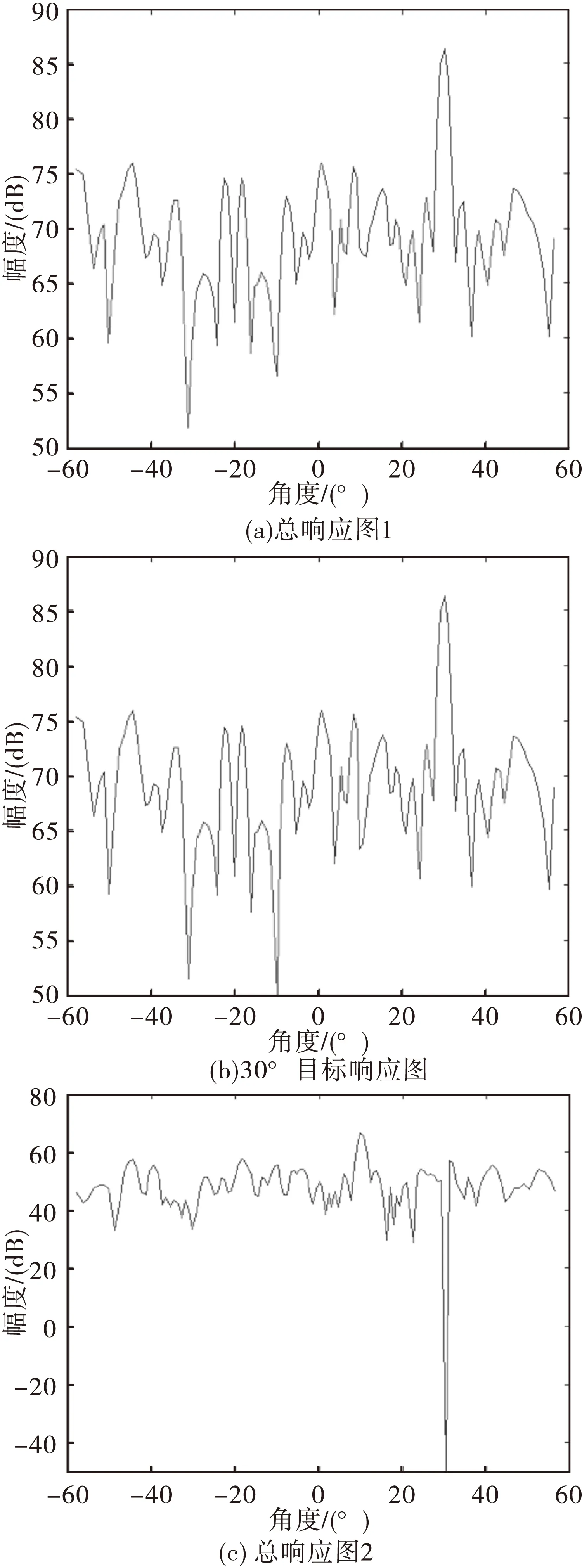
圖3　FAC結果圖

實驗四：兩個目標角度選為10°和30°，SNR相等，都是從10dB變化到70dB，間隔為1dB，實驗結果如圖4所示。

由圖4可以看出，當兩目標入射角度相差較大，且SNR相同時，FAC和RM的精度都很高，FAC優于RM，且FAC與RM都對SNR變化不敏感。

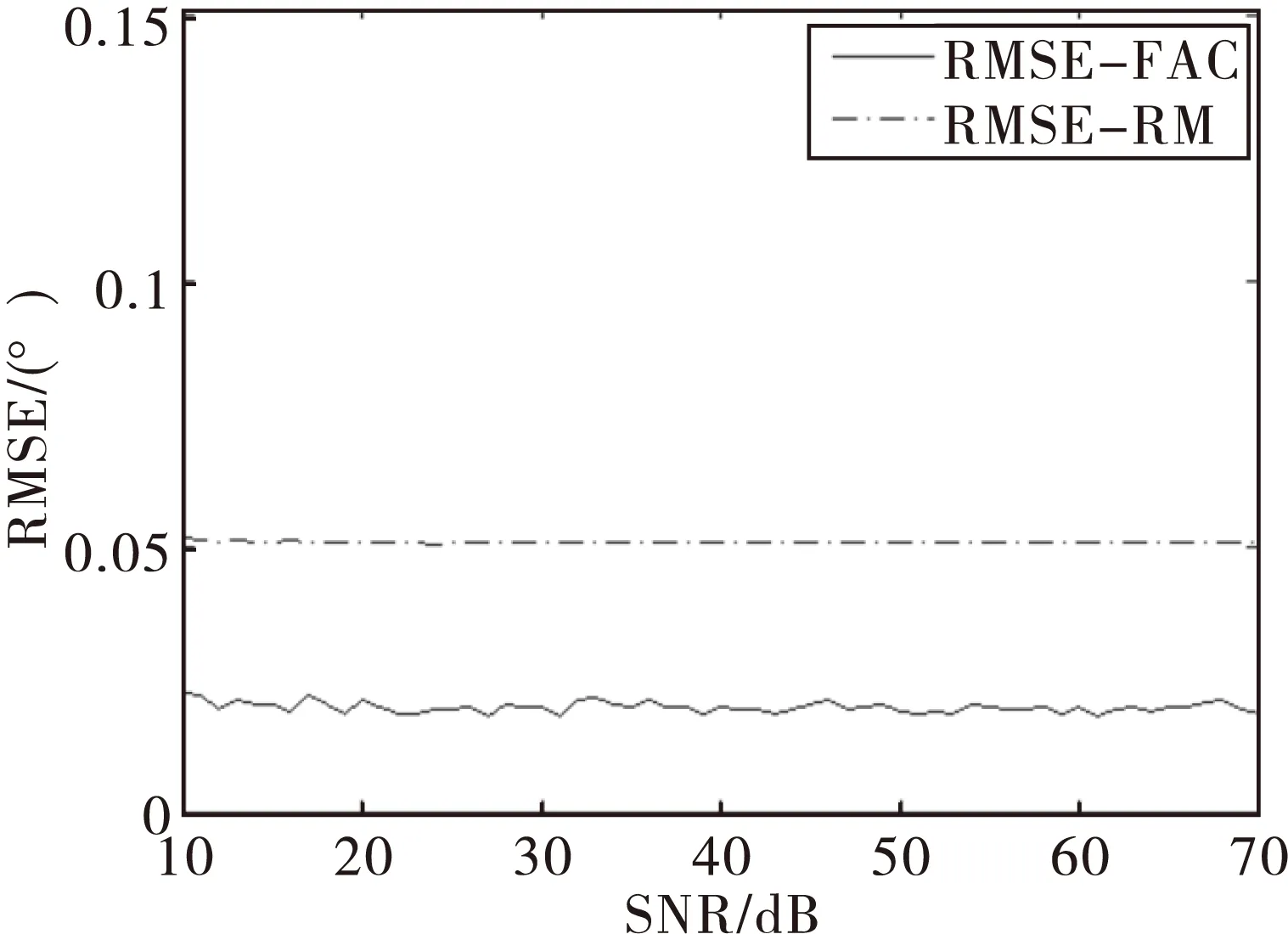
圖4　實驗四結果圖

實驗五：為驗證目標SNR相同，角度接近時FAC算法的性能，兩目標的SNR都選為20dB，一個目標的入射角度固定為20°，另一個目標的入射角度從20.15°變化到26°，間隔為0.1°，實驗結果如圖5所示。

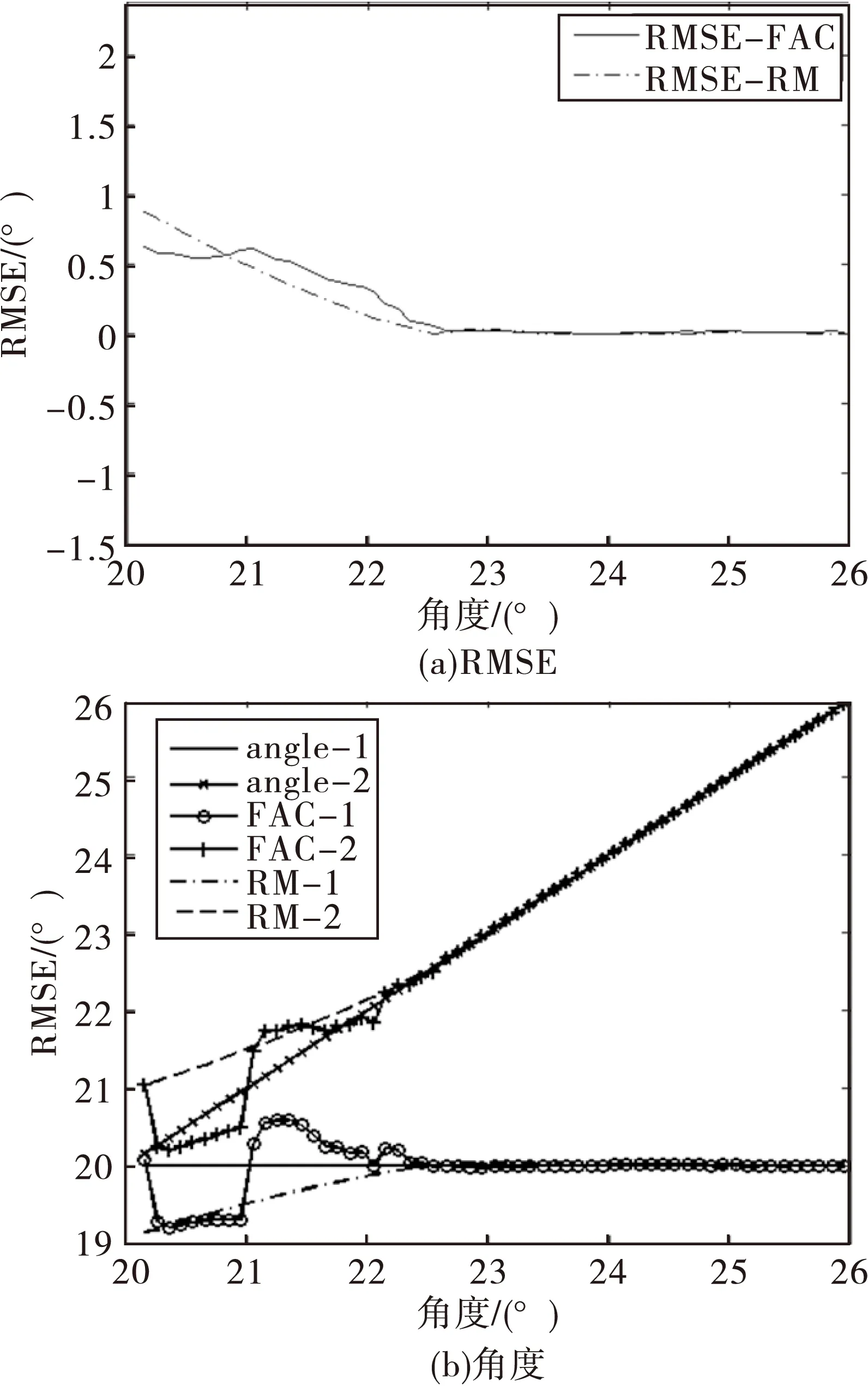
圖5　實驗五結果圖

由圖5(a)可以看出，當SNR相同，兩個目標入射角度很接近時，RM和FAC效果都比較差，在角度十分接近時FAC效果較好，隨著角度的增加，逐漸變得RM效果較好，當角度相差較大時，二者效果都很好。

圖5(b)中實線(angle-1)和虛線(angle-2)表示兩個目標的真實角度，觀察FAC和RM求得的角度,可以看出，在兩個目標角度相近時，FAC和RM都不是很精確。當兩目標入射角度相差較大時，FAC和RM都很精確。

實驗六：為驗證目標SNR不同，角度接近時FAC算法的性能，第一個目標的SNR取為20dB，第二個目標的SNR取為25dB，第一個目標的入射角度固定為20°，第二個目標的入射角度從20.15°變化到26°，間隔為0.1°，實驗結果入圖6所示。

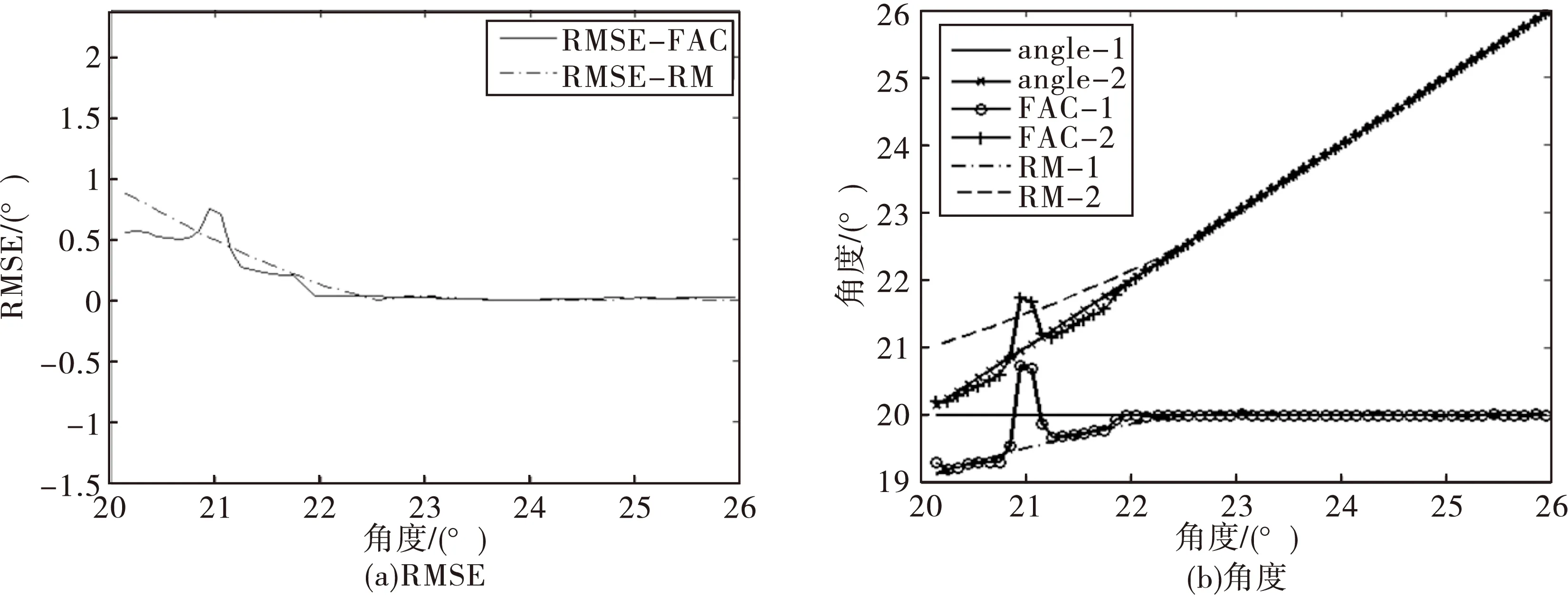
圖6　實驗六結果圖

由圖6(a)可以看出，當兩個目標的SNR不同時，在入射角度比較近時，大多數情況下FAC的結果優于RM的結果。從圖7(b)可以看出，當兩目標的SNR不同時，在大多數情況下，FAC算法幾乎可以精確的估計出SNR較高的那個角度，而另一個角度的值和RM估計的基本一致。

3　結束語

本文針對稀疏陣旁瓣比較高的問題，提出了一種基于CLEAN的DOA估計方法。實驗結果表明，本文所提出的算法耗時很少，且耗時對陣元數不敏感，對目標角度的估計精度很好，能夠很好的抑制稀疏陣強目標與高旁瓣作用結果對弱目標角度估計的影響。