寧波軟土地區基坑數值計算中HS模型參數試驗研究

楊蘭強， 周立波， 夏　雯， 管仁秋， 張　浩， 羅偉錦

(1. 浙江省工程勘察院， 浙江 寧波　315000； 2. 國網寧波供電公司， 浙江 寧波　315010)

0　引言

隨著城市的快速發展，土地已成為稀缺資源，在建筑向高空發展的同時，地下空間的利用也必然成為一個重要方向。基坑工程經常鄰近敏感的建(構)筑物，如地鐵、頂管電力隧道、淺基礎建筑和橋梁等。面臨這些問題時，基坑支護結構除了需滿足強度要求外，還需滿足變形要求，以保護周圍的建(構)筑物，而目前規范提供的方法并不能解決基坑開挖對周圍環境的影響[1-2]。

隨著有限單元法的發展，有限元已逐漸成為解決基坑變形預估問題的主要方法，而有限元數值模擬方法的核心問題之一是選取合適的土體本構模型和計算參數。目前，對于軟土地區基坑工程的數值模擬，HS模型(hardening soil model)具有明顯的適應性[3-4]。王培鑫等[5]借助有限元方法結合監測結果，驗證了土體HS模型在評估基坑開挖對鄰近鐵路變形影響的數值模擬中的適用性。姜寶臣等[6]借助MIDAS GTS有限元軟件以及理正深基坑軟件分析總結了復雜敏感環境下的深大基坑采用土體HS模型數值模擬獲取的結果，同時指出土體參數選取是關鍵。白成生[7]利用Plaxis 軟件以及HS模型分析了基坑工程的變形特性，并對各本構模型進行了對比分析。由于HS 模型采用雙曲線擬合應力和應變特性，能夠反映土體的非線性特性，而且HS 模型采用與應力相關的模型參數，能夠反映基坑工程不同的應力路徑，因此，HS 模型比較適用于深基坑工程的計算分析。劉暢[8]從土體不同強度、變形參數以及基坑空間效應角度考慮，驗證了土體HS模型與實際結果較為吻合。

HS模型參數較多，想要獲取完整的模型參數非常困難，而目前HS模型參數主要通過工程實際監測數據反分析或通過室內土工試驗得到，其中，室內土工試驗法能直接測得土體的物理力學性質指標，更真實地反映土體的實際狀態。王衛東等[9]通過固結試驗、三軸試驗等手段較完整地總結了上海軟土地區的HS模型參數。由于巖土材料具有明顯的地域性，對于寧波軟土地區尚無關于HS模型參數的報道。為此，本文將對寧波典型軟土開展室內土工試驗獲取其HS模型參數，并對其模量關系進行分析，以期為寧波地區類似基坑工程數值模擬提供參考。

1　土體HS模型及其參數求解

HS模型是由T.Schanz在P.A.Vermeer的雙硬化模型基礎上提出的一種等向硬化彈塑性模型，該模型可以同時考慮剪切硬化和壓縮硬化，并滿足Mohr-Coulomb破壞準則[10]。

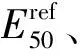
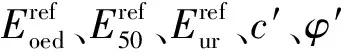
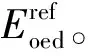
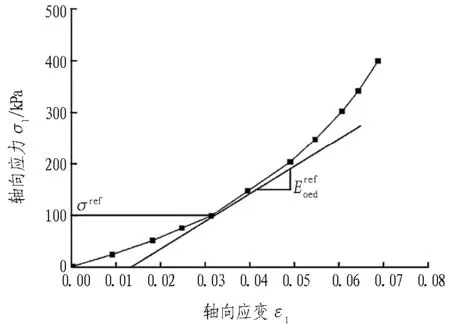
圖1　由標準固結試驗σ1-ε1 曲線定義的

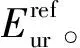
Fig. 2Hyperbolic stress-strain relationship in primary loading for a standard drained triaxial test

(1)

(2)

式中：qf為土體強度偏應力；qa為土體極限偏應力；σ1、σ3分別為土體軸向應力和圍壓；c′為有效黏聚力；φ′為有效內摩擦角。

2　試驗內容及試驗方案

2.1　試驗材料

寧波為典型的軟土地區，基坑范圍內各土層起伏不大。寧波城區13個建筑工地的土層物理力學參數見表1。由表1可知，基坑開挖范圍內主要涉及的是第1層粉質黏土(局部為黏土)，與雜填土相連，土層厚0.5～1.6 m。其下為第2層淤泥質粉質黏土(局部會出現淤泥質黏土)，其中，第2層土又細分為②1、②2、②3，但總體土性差別不大，第2層土厚度9.4～24.3 m，寧波幾乎所有的基坑工程均受這層土影響。再往下為第4層粉質黏土和第5層粉質黏土，局部會出現黏土層，其中，第4層土局部地區會缺失。2層土土層厚度8.2～68.6 m，其中，第5層土又細分為⑤1、⑤2和⑤3，總體土性差別不大。

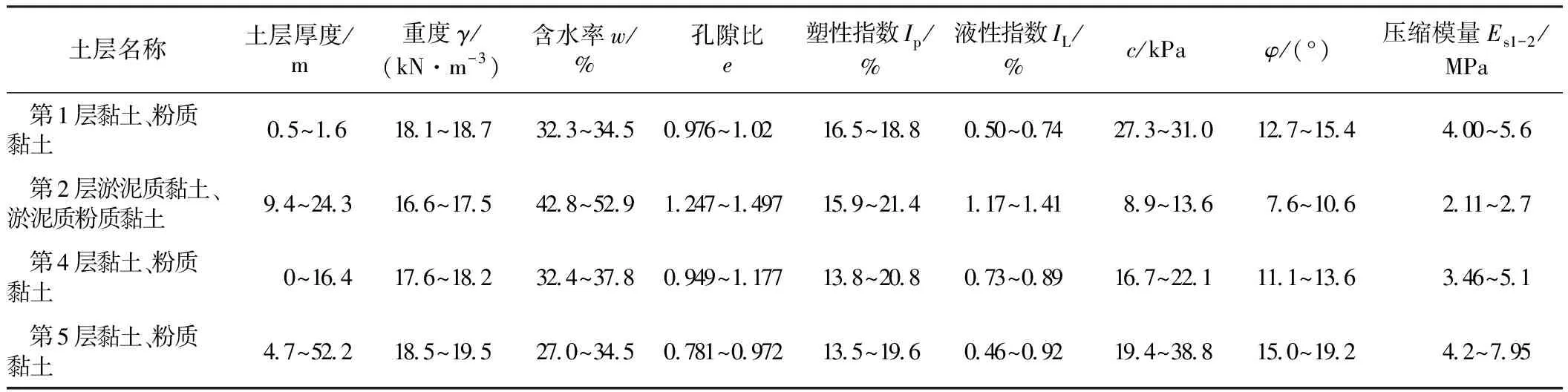
表1　寧波城區典型土層物理力學參數

對于基坑工程而言，寧波城區的土層以淤泥質土、粉質黏土為主。為此，試驗材料取自寧波地區某一建筑工地的2種典型土層(淤泥質土、粉質黏土)為試樣，并對采集的試樣開展基本物理性質試驗，如表2所示。采集的淤泥質土及粉質黏土的試樣照片見圖3。

表2　采集土樣的基本物理參數指標

圖3　采集的淤泥質土、粉質黏土試樣

2.2　試驗方案及步驟

試驗在浙江大學寧波理工學院的土工實驗室進行。對采集的淤泥質土和粉質黏土試樣分別進行標準固結試驗、三軸固結排水剪切試驗(CD)和三軸固結排水加載—卸載—再加載試驗。試驗設備如圖4所示。

(a) 三軸試驗儀

(b) 固結試驗儀

1)標準固結試驗步驟： 淤泥質土做3組，制樣密度按1.73 g/cm3控制，試樣初始含水率w0按30 %、35%和40%3種進行控制。粉質黏土做3組，制樣密度按1.91 g/cm3控制，試樣初始含水率w0按20%、25%和30%3種進行控制。

給試樣施加不同等級的荷載，試驗采用5 級荷載，分別為50 kPa、100 kPa、200 kPa、400 kPa和800 kPa，每級荷載固結穩定時間取24 h。

2)三軸固結排水剪切試驗步驟：淤泥質土選取3種圍壓，分別為100 kPa、200 kPa和300 kPa。制樣密度按1.73 g/cm3控制，試樣初始含水率w0按35%控制。粉質黏土選取3種圍壓，分別為50 kPa、100 kPa和200 kPa。制樣密度按1.91 g/cm3控制，試樣初始含水率w0按30 %控制。

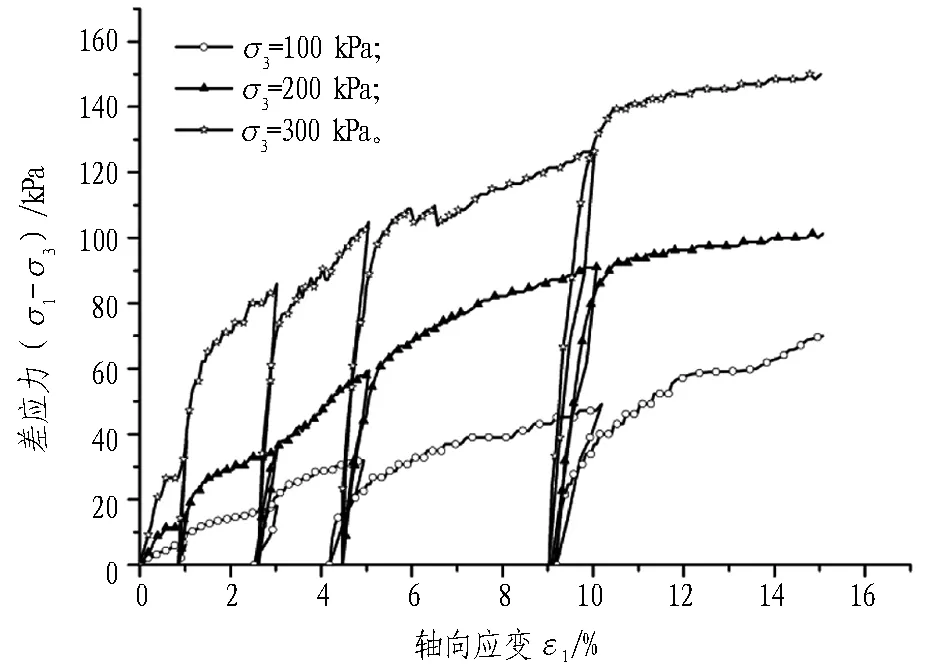
采用位移控制，軸向剪切速率為0.003 7 mm/min。當軸向應變達到17 %時或出現明顯峰值后結束試驗。試驗期間上下孔隙水閥始終打開，保持排水順暢，測其差應力-軸向應變和體應變-軸向應變的關系。

3)三軸固結排水加載—卸載—再加載試驗步驟： 淤泥質土選取3種圍壓，分別為100 kPa、200 kPa和300 kPa。制樣密度按1.73 g/cm3控制，試樣初始含水率w0按35%控制。粉質黏土選取4種圍壓，分別為50 kPa、100 kPa、200 kPa和300 kPa。制樣密度按1.91 g/cm3控制，試樣初始含水率w0按30%控制。

在相同圍壓下，每個試樣需在4個軸向應變(即軸向應變ε1達到1%、3%、5%和10%)時分別進行卸載—再加載試驗，當軸向應變達到17%時或出現明顯峰值時結束試驗。試驗期間上下孔隙水閥始終打開，保持排水順暢。

3　試驗結果及參數確定

3.1　標準固結試驗結果及參數確定

寧波淤泥質土、粉質黏土試樣的標準固結試驗e-p曲線見圖5。由圖5可知，寧波淤泥質土在不同孔隙比的初始條件下，隨著軸向力p的不斷增大，3種不同初始孔隙比的e-p曲線很快重合成1條曲線。而寧波粉質黏土由于土體強度、模量均大于淤泥質土，所以3種不同初始孔隙比的e-p曲線未能很快重合成1條曲線，但隨著軸力p的不斷增大，其重合的趨勢明顯。從圖5可得知寧波淤泥質土試樣在荷載間隔p1=100 kPa至p2=200 kPa時，對應的壓縮模量Es1-2為2.55～2.73 MPa。寧波粉質黏土試樣在荷載間隔p1=100 kPa至p2=200 kPa時對應的壓縮模量Es1-2為2.94～5.35 MPa，而且這2種土層試樣的壓縮模量Es1-2隨初始孔隙比e0增大而減小，充分表現土體密實度越高，壓縮模量越大的特點。

寧波淤泥質土、粉質黏土試樣的標準固結試驗軸向荷載與軸向應變的關系曲線見圖6。由圖6可知，不同初始孔隙比e0下的寧波淤泥質土、粉質黏土的軸向應力p與軸向應變ε1的關系曲線可由式(3)擬合。

p=keηε1。

(3)

式中k、η為試驗擬合參數。

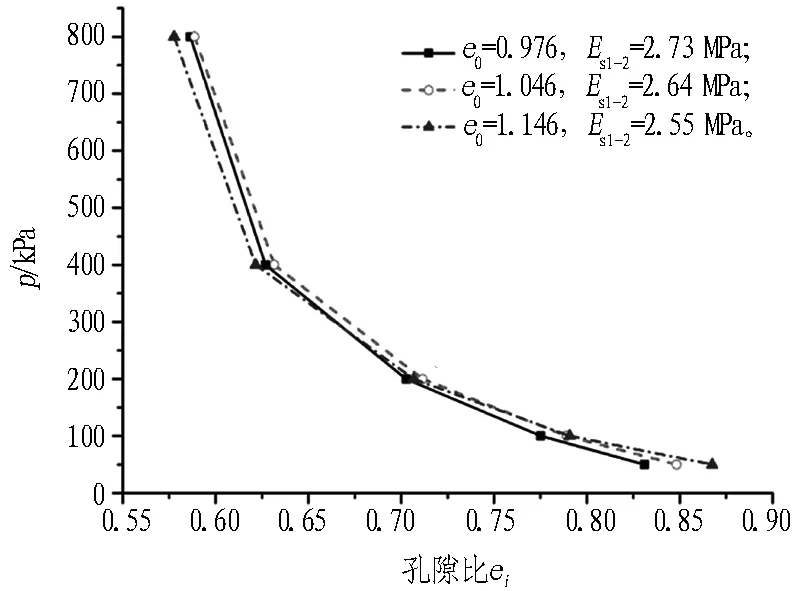
(a) 寧波淤泥質土

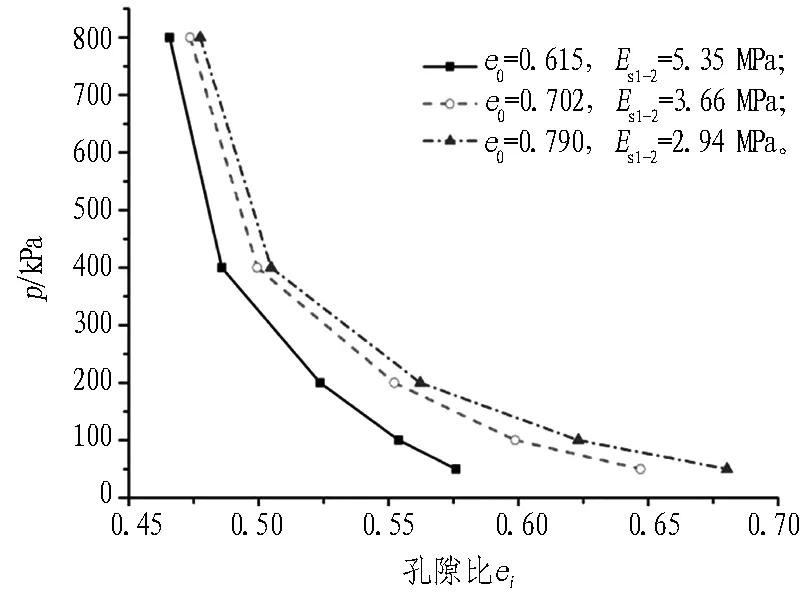
(b)寧波粉質黏土

Fig. 5Relationships between load and void ration of soil layers in consolidation test

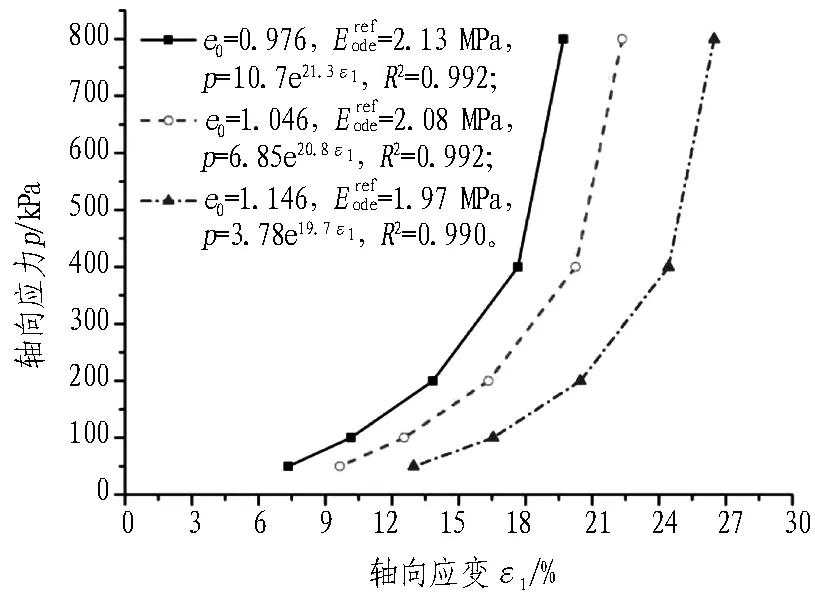
(a) 寧波淤泥質土

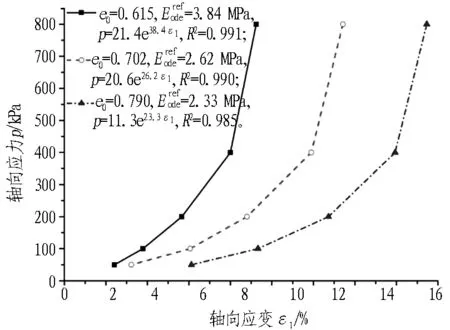
(b) 寧波粉質黏土

3.2　三軸固結排水剪切試驗結果及參數確定

寧波淤泥質土、粉質黏土試樣的三軸固結排水剪切試驗的差應力與軸向應變的關系曲線見圖7。由圖7可知，寧波淤泥質土隨著圍壓的逐漸增大，其應力-應變曲線表現為應變軟化型，而粉質黏土表現為應變硬化型。根據Konder的建議，其土體試樣的應力-應變曲線可擬合出雙曲線函數

(4)

式中a、b為試驗擬合參數。

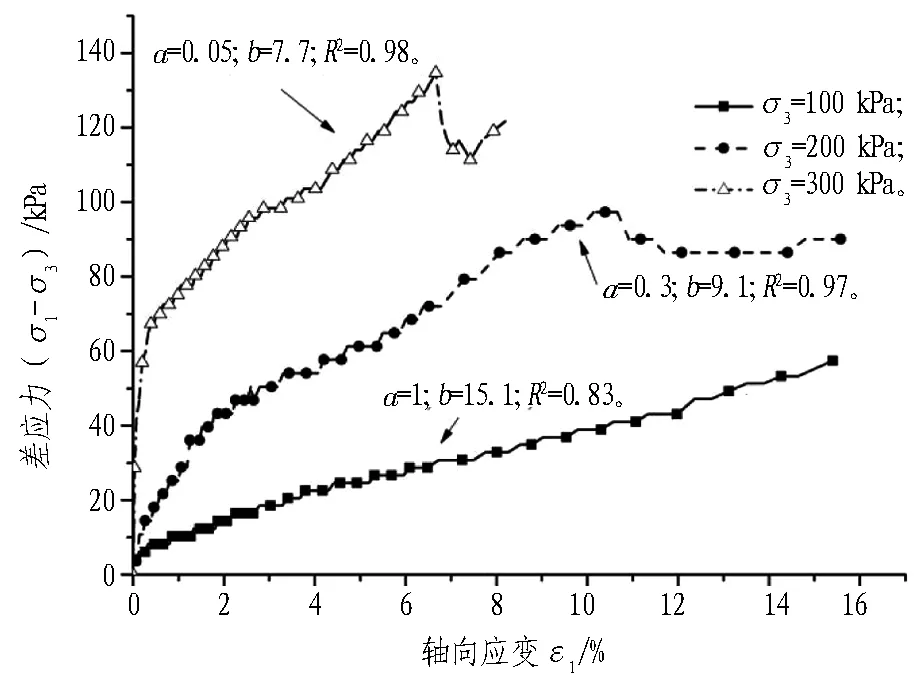
(a) 寧波淤泥質土

(b) 寧波粉質黏土

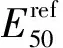
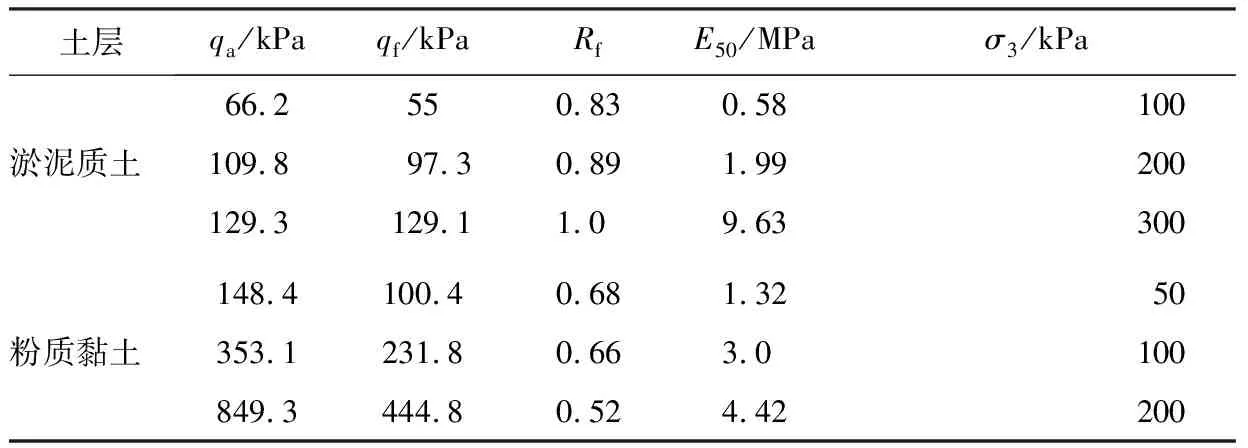
表3　各土層試樣計算參數統計表

3.3　三軸固結排水加載—卸載—再加載剪切試驗結果及參數確定

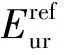
3.4　試樣抗剪強度

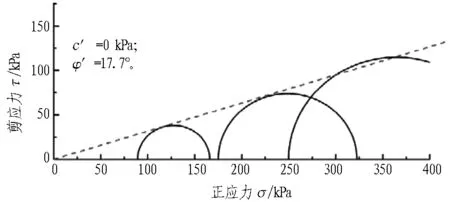
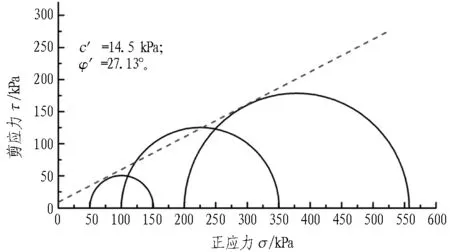
寧波淤泥質土和粉質黏土試樣在不同圍壓下的摩爾圓和抗剪強度包絡線見圖9，試驗結果符合

τf=σtanφ′+c′。

(5)

式中:φ′為有效內摩擦角，°；c′為有效黏聚力，kPa。

一般認為，對于三軸固結排水試驗，正常固結軟黏土的黏聚力c′≈0[15]，所以，對于寧波淤泥質土的強度

τf=σtanφ′。

(6)

計算得到寧波淤泥質土的有效黏聚力c′為0 kPa，有效內摩擦角φ′為17.7°。粉質黏土的有效黏聚力c′為14.5 kPa，有效內摩擦角φ′為27.13°。

由于目前勘察報告一般僅提供固結快剪試驗的c、φ值，與表1統計的數值大體相當，因此，HS模型中的c、φ值采用勘察報告提供的固結快剪試驗的c、φ值是合適的。

(a) 寧波淤泥質土

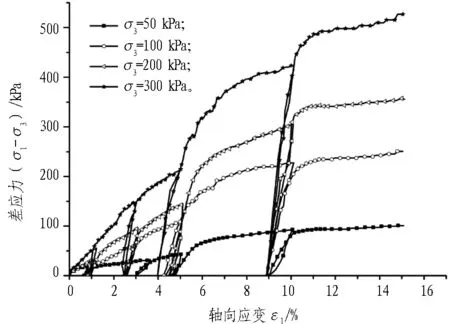
(b) 寧波粉質黏土

Fig. 8Strain-stress curves of triaxial CD loading-unloading-reloading test of each sample

(a) 寧波淤泥質土

(b) 寧波粉質黏土

4　HS模型參數取值討論

4.1　寧波土層各模量之間關系

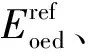
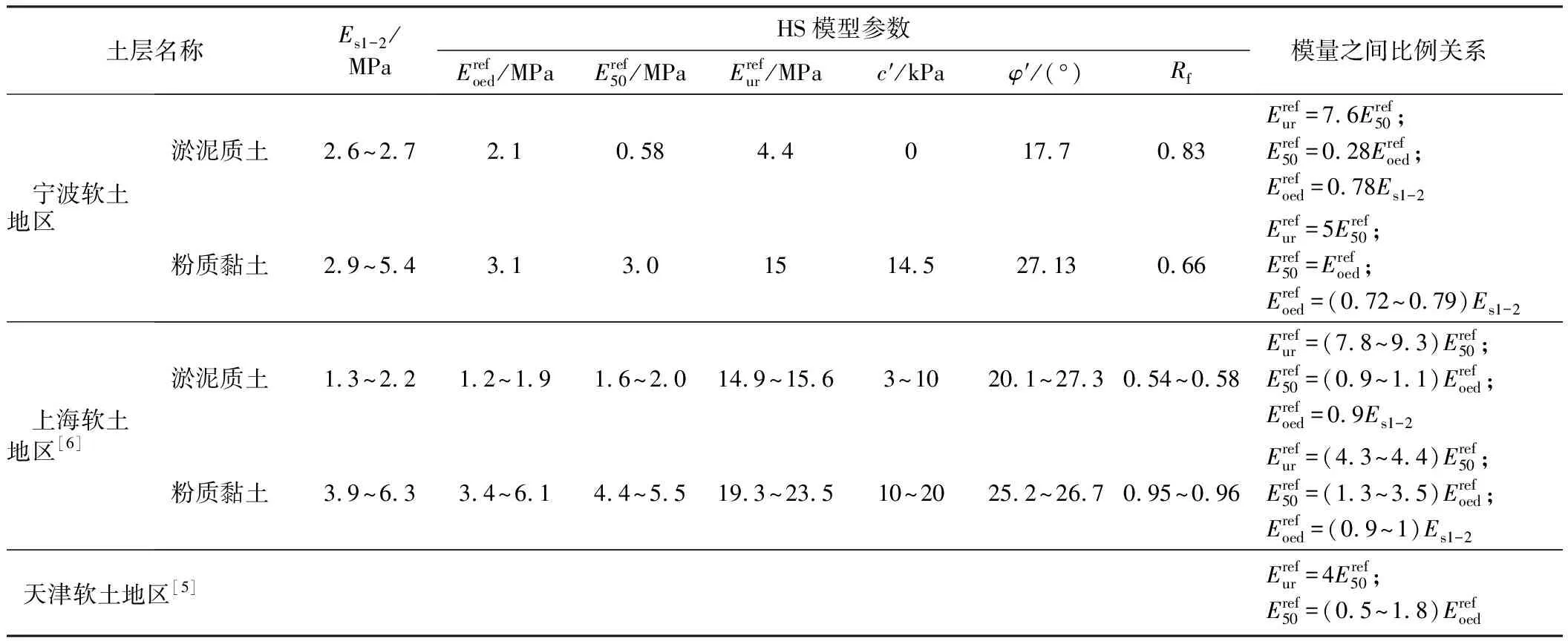
表4　土體HS模型參數對比表

表4中還給出了上海軟土地區及天津軟土地區的HS模型參數。由表4可知，寧波地區的淤泥質土、粉質黏土與上海地區的淤泥質土、粉質黏土的壓縮模量Es1-2大體相當。寧波地區的淤泥質土的有效內摩擦角φ′小于上海地區的淤泥質土的有效內摩擦角。易坤津[16]、趙國強[17]通過大量的工程實踐統計，也同樣發現這一規律。此外，對于淤泥質土的孔隙比、含水率，整體上寧波高于上海和天津，而滲透性遠低于上海和天津。

淤泥質土、粉質黏土的破壞比Rf寧波地區與上海地區有明顯差異。土體破壞比Rf是土體強度偏應力與土體極限偏應力的比值，其中，土體強度偏應力是按峰值強度或15%軸向應變取值；土體極限偏應力概念的前提是假設土體滿足雙曲線規律。為此，寧波地區和上海地區的淤泥質土、粉質黏土的破壞比Rf的差異本身無概念意義，但可直接說明寧波地區和上海地區的淤泥質土、粉質黏土的應力-應變關系曲線存在較大差異，間接說明地區土體的差異性。

4.2　工程實例驗證

4.2.1工程概況

選取寧波城區的新典路過街通道的基坑實例進行驗證。該項目位于寧波市鄞州區長豐橋南端，擬建地下通道的基坑深度5.9～12.05 m，基坑開挖范圍內土體以淤泥質土、粉質黏土為主。基坑支護采用φ900～1 100@1 200～1 300 mm鉆孔灌注樁+4道支撐的形式。其中，第1道支撐為鋼筋混凝土支撐，其余3道支撐為609鋼管支撐。鉆孔灌注樁樁長19～23 m，具體如圖10所示。

圖10　新典路過街通道基坑實例

該基坑鄰近1條頂管電力隧道，要求基坑變形對頂管電力隧道的變形影響控制在20 mm以內。該頂管電力隧道為混凝土管節結構，隧道直徑為3 m，管壁厚250 mm，管節長2.5 m，管節間的連接方式為預埋鋼套環F型承插式接頭，橡膠止水，埋深為7.69～8.35 m。基坑邊距離電力隧道6.5～13 m。

4.2.2數值計算模型及其參數

采用MIDAS/NX三維有限元軟件對新典路過街通道基坑進行模擬分析，其土體本構模型采用HS模型，參數按照表4統計的關系式確定。

基坑支護結構和電力隧道結構單元網格見圖11，由圖可知，基坑支護鉆孔樁采用剛度等效的原理模擬，等效為地下連續墻，采用板單元進行模擬，支撐和環梁采用梁單元進行模擬。頂管電力隧道的管片采用板單元進行模擬。

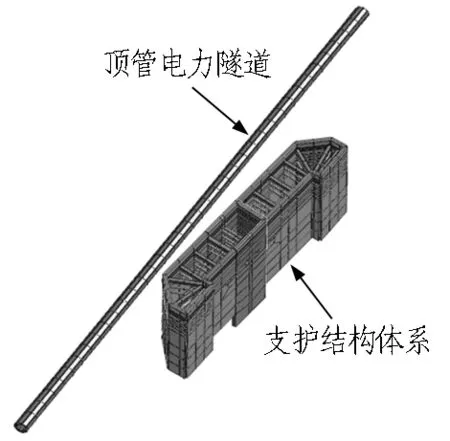
圖11　基坑支護結構、頂管電力隧道結構單元網格圖

土體三維實體單元模型見圖12，由圖12可知，基坑內外土體均采用實體單元(4節點單元)進行模擬。該模型尺寸為110 m×150 m×40 m(長×寬×高)。邊界條件為土體左右、前后界面上固定x、y方向的位移；底部界面固定x、y、z方向的位移。

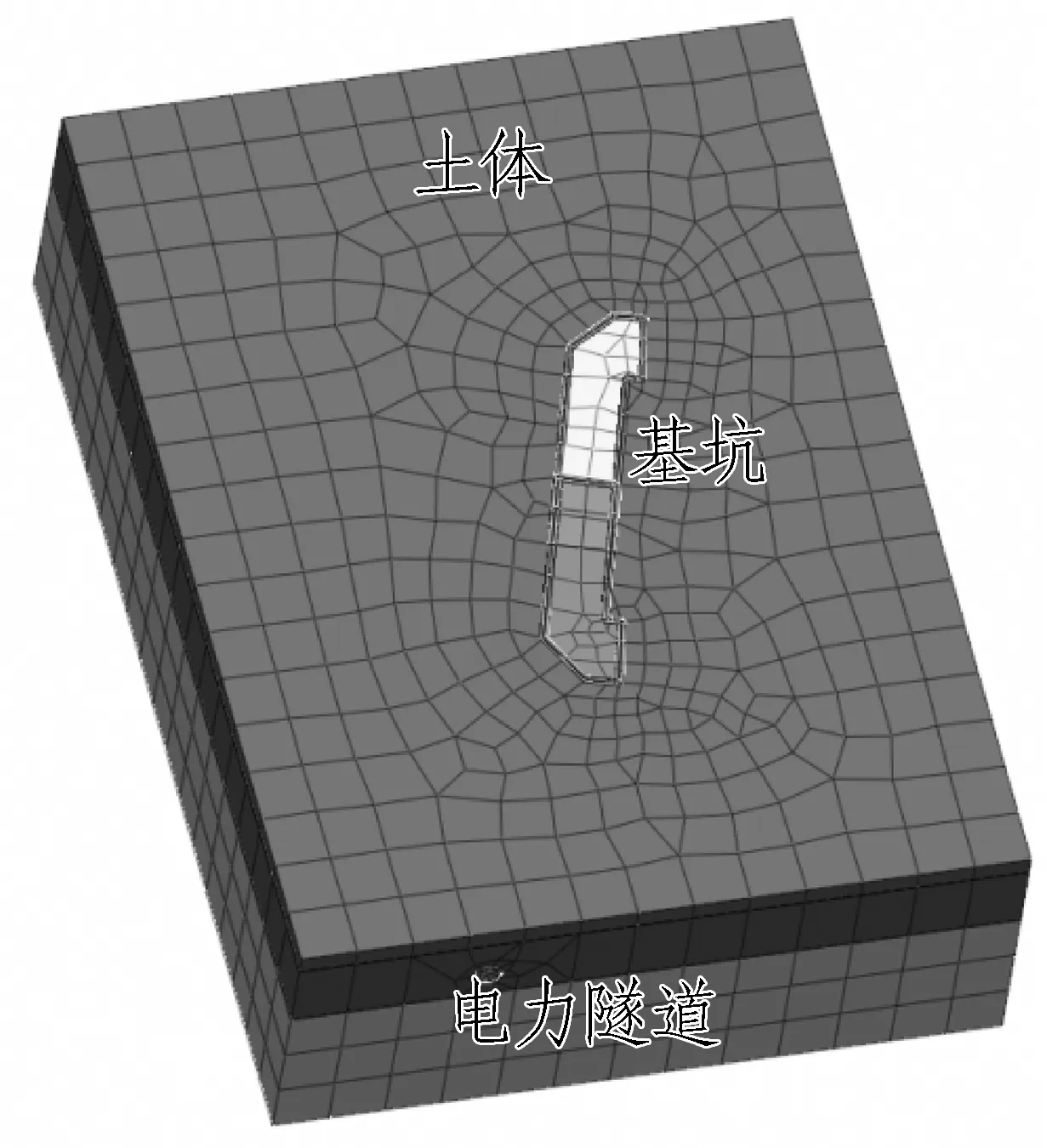
圖12　土體三維實體單元模型

4.2.3模擬結果與驗證

文獻[4]較系統地總結了基坑數值模擬中較常用的土體本構模型，并根據算例分析了各本構模型的適用性。該研究指出，彈-理想塑性M-C模型和D-P模型由于采用單一剛度，導致墻體變形及墻后變形過大，與實際差別較大。而修正劍橋模型、HS模型考慮了土體應變硬化特征，能區分加荷與卸荷的區別，且考慮剛度依賴于應力歷史和應力路徑的情形，基坑數值模擬中模擬的墻體變形及墻后土體變形情況與實際較吻合，但由于HS模型需要輸入的參數較多，因此，選用合適的土體參數是關鍵。

支護樁水平位移和頂管電力隧道位移對比分別見圖13和圖14。由圖13和圖14可知，當基坑開挖至坑底(深度5.9 m)時，實際監測的支護樁水平最大位移為23.1 mm，而數值模擬的結果為24.5 mm。鄰近的頂管電力隧道實際監測最大位移為4.6 mm，而數值模擬的結果為5.1 mm。基坑按實際工況進行模擬，模擬基坑開挖至基坑底，之后的主體結構向上施工、土方回填等工況對支護結構變形、鄰近的頂管電力隧道變形影響不大，故之后的工況本次未模擬。結果說明在寧波軟土地區，當采用土體HS本構模型以及表4總結歸納的土體參數時，其基坑開挖數值模擬的墻體變形及墻后建(構)筑物變形情況與實際較為吻合，從而驗證了HS模型以及總結的土參數在寧波軟土地區基坑開挖數值模擬中的適用性。

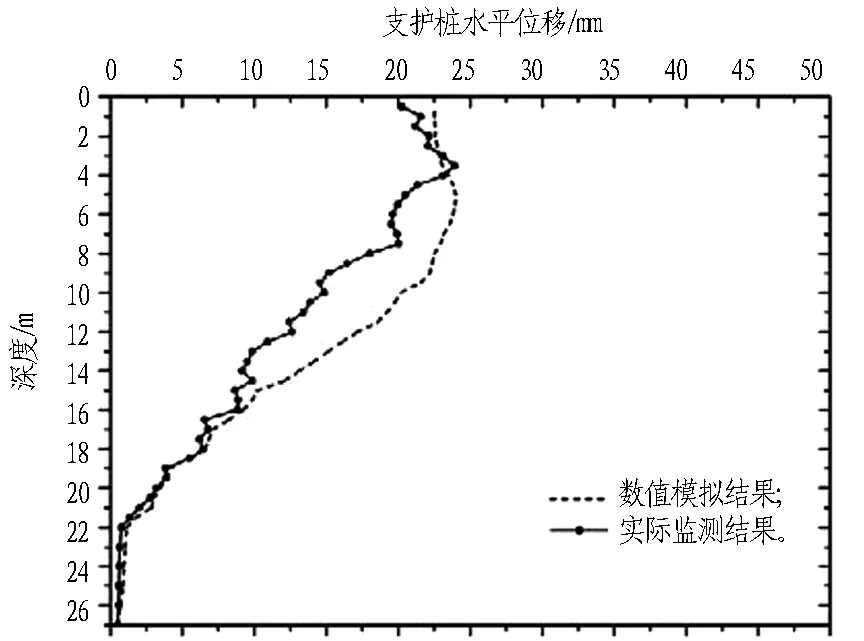
圖13　支護樁水平位移對比圖

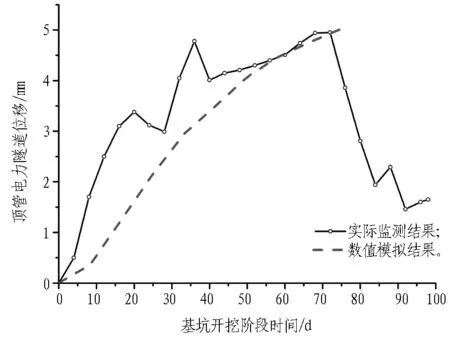
圖14　頂管電力隧道位移對比圖

Fig. 14Comparison of displacements of pipe-jacking power tunnel

5　結論與討論

通過選取寧波典型的2種土層(淤泥質土、粉質黏土)，開展標準固結試驗、三軸固結排水剪切試驗和三軸固結排水加卸載試驗，獲得了寧波地區典型軟土的HS模型參數數值，以及模型參數之間的比例關系，主要結論如下：

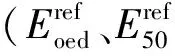
3)對寧波新典路過街通道深基坑工程進行三維分析，計算結果與實測數據較為接近，從而驗證了HS 模型及本文統計的HS參數在寧波地區基坑開挖數值計算中的適用性。

4)由于巖土材料的離散性較強，對于寧波地區土體參數，尤其是HS模型中幾個模量之間的關系，還需要通過開展大量的土工試驗以獲取統計學規律。