客運專線縱斷面線形重構的思路與方法
楊嘉岳, 周 錟, 楊文昕
(西南交通大學土木工程學院, 四川成都 610031)
客運專線具有高平順性、高穩定性的特點,但是在多年的運營和維護后,客運專線的線路難免會發生偏移,線路的平順性受到影響,在線路的平面曲線地段和縱斷面豎曲線地段,軌道的幾何形位和線形的改變相對于直線地段尤為明顯,目前針對平面線形的重構已經取得了較多的成果[1-3],提出了根據曲率、斜率、方位角等參數的變化對平面線形進行分段,結合迭代擬合[4]的思想,實現了平面線形的重構,在縱斷面線形的重構中,擬根據相同的思路,首先對縱斷面線形的里程和高程數據進行測設,在得到滿足測設精度要求的各項數據后,對縱斷面測設數據進行粗略分段和精確分段,在此基礎上,根據縱斷面起落道量在直線地段為點位到擬合直線的距離,在曲線地段為點位到擬合的豎圓曲線圓心的距離與半徑的差值,進行縱斷面起落道量的計算,恢復縱斷面線形的平順性,以滿足客運專線的平順、安全和舒適。
1 里程與高程數據的測設
客運專線對線路的平順性要求相對于普速鐵路更高,意味著對測設點位的里程數據與高程數據提出了更高的精度要求,隨著現代測量技術的發展,在客運專線中線的測量中,已經有比較多的成熟的測量技術,通過全站儀和軌檢小車系統,在軌道控制網的基礎上,對客運專線線路中線的里程與高程數據以及對應里程處左右鋼軌的高程數據進行測量,得到眾多高精度的線路中線、左右鋼軌里程與高程數據。
客運專線對平順性的要求比普速鐵路更高,需要測量得到的里程數據與高程數據盡可能全面地體現縱斷面的實際位置,因此測設數據點位之間的里程間隔應該足夠小,相鄰測點的間隔可以考慮取為一個軌枕間距0.625 m,在高精度高密度的線路中線、左右鋼軌里程與高程測量數據的基礎上,展開客運專線縱斷面線形重構的探討,為恢復客運專線在縱斷面上的平順性提供一定的參考。
2 縱斷面線形分段
在進行縱斷面線形重構前,汲取平面線形重構的經驗[5],首先需要根據縱斷面線形的特點,對縱斷面線形進行分段,鑒于基準鋼軌縱斷面線形不受超高的影響,故縱斷面線形的重構擬針對基準軌展開。在基準軌縱斷面線形中,最明顯的特征即是相鄰直線坡段坡度發生改變,故可以根據坡度的變化對基準軌縱斷面線形進行粗略分段。
在粗略分段完成的基礎上,為了提高線形重構的準確性,需要提高線形分段的精確程度,故在粗略分段的基礎上,展開線形的精確分段。
在平面線形的精確分段中,迭代擬合的思想應用廣泛,在平面線形的精確分段中取得了很好的效果,線形分段的精確程度達到了一個軌枕間距0.625 m以內。在縱斷面線形的精確分段中,擬采用同樣的思路,實現縱斷面線形的精確分段。
2.1 粗略分段
粗略分段即根據測設點位信息,對其歸屬做出大致判斷,不要求達到非常高的精度,只需粗略分段結果能滿足后續的線形擬合即可。粗略分段流程如圖1所示。

圖1 粗略分段流程
粗略分段步驟:
(1)根據實測里程與高程數據計算一定間隔的測點位置的坡度大小;
(2)繪制坡度圖,并根據坡度變化規律確定直線坡段的近似坡度大小與分段點位置的近似里程,主要依據為:由上一直線坡段過渡到下一直線坡段的過程中,坡度發生明顯的變化,在直線坡段,坡度理論上為定值,由于線形可能發生改變,故直線坡段的坡度將在某一定值附近波動,故可根據此變化規律確定坡度近似值與分段點近似里程位置。
2.2 精確分段
精確分段需對測設數據的歸屬盡可能地做出準確的判斷,直至最終確定的分段點里程不再影響數據的分段結果,即連續兩次確定的分段點的里程差值不超過限值,限值可根據實際需求確定,精確分段流程如圖2所示。

圖2 精確分段流程
精確分段步驟:
(1)在粗略分段的基礎上,將測設點位數據分為豎圓曲線段和兩側相切直線坡段三種區段,對各自坡段內的測點數據分別進行線形的擬合,通過擬合得到豎圓曲線圓心位置、豎圓曲線半徑以及豎圓曲線兩側直線坡段的斜率和截距;
(2)在擬合結果的基礎上,根據直線坡段擬合結果,計算變坡點里程位置與坡度代數差;
(3)根據豎圓曲線擬合結果,計算豎圓曲線切線長,以此確定分段點里程位置;
(4)根據分段點里程位置,對測設點位數據重新進行分段,并參與到各自對應線形的擬合中去,當連續兩次得到的分段點里程差值不超過確定的限值時,即認為縱斷面線形的分段達到了精確分段的效果。
3 縱斷面線形擬合
在縱斷面線形分段中,將涉及到到直線線形與圓曲線的擬合問題,需采用不同的模型分別進行擬合計算。
3.1 擬合模型
直線線形的擬合模型為:
Y=kX+b
式中:k為直線斜率;b為直線截距。
豎圓曲線的擬合模型為:
(X-XO)2+(Y-YO)2=R2
式中:XO為豎圓曲線圓心O的里程;YO為豎圓曲線圓心O的高程。
擬合問題中,需要找到使得誤差達到最小的直線和豎圓曲線的線形表達式,常用的衡量標準為偏差的平方和達到最小:
式中:ri為任意點位的偏差。
3.2 擬合方法
在曲線的擬合中,常用的擬合方法[6]主要有以下三種。
3.2.1最小二乘法
最小二乘法基于最小二乘原理,認為點位的橫坐標或者縱坐標存在但并不同時存在偏差,并使得偏差的平方和最小,下面以直線的擬合來說明。
當橫坐標作為自變量時,基于最小二乘法的偏差如圖3所示。

圖3 最小二乘法沿Y軸方向的偏差
當縱坐標作為自變量時,基于最小二乘法的偏差如圖4所示。
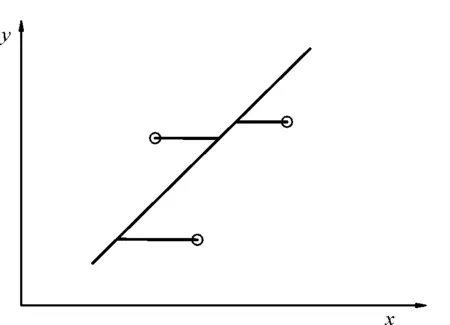
圖4 最小二乘法沿X軸方向的偏差
3.2.2基于距離最短的最小二乘法
在最小二乘法的基礎上,將偏差視作點到直線的最短距離,則基于距離最短的最小二乘法的偏差如圖5所示。

圖5 基于距離最短的最小二乘法的偏差
3.2.3引入穩健評估的最小二乘法
在基于距離最短的最小二乘法的基礎上,引入穩健評估,即根據偏差的大小,給每個測設點位數據一個新的權重,降低偏差較大的點位對擬合結果的影響。
在基于距離最短的最小二乘法的基礎上引入穩健評估,可以減小偏差較大的測設點位數據對擬合結果的影響,效果優于上述兩種擬合方法。
結合縱斷面線形可能存在一些點位發生了較大偏差的情況,因此,在縱斷面線形的擬合中,可以考慮采用引入穩健評估的最小二乘法來分別擬合縱斷面線形中的直線和豎圓曲線,得到更加優化的線形擬合參數。
4 縱斷面線形的優化
在縱斷面線形分段和擬合的基礎上,可以得到滿足偏差最小的直線和縱斷面擬合線形,但是在縱斷面中,還包含了縱多的約束條件,比如豎曲線與平面緩和曲線不得重合,豎圓曲線與道岔位置不能重合,縱斷面中某些點位的最大高程和最小高程滿足要求,擬合結果中的直線坡度不得超過允許的最大坡度等,考慮養護維修時,還應對縱斷面的直線坡度大小以及豎圓曲線半徑大小的取值精度進行約束,即需要對直線線形與豎圓曲線線形擬合結果進行一定的調整,以滿足規范和養護維修的要求。
在滿足所有約束條件后,得到的直線和豎圓曲線擬合結果才是滿足實際工程需求的最終擬合結果,在此基礎上,通過計算各個測設點位的起落道量,并將點位恢復至擬合后的參考線形位置,恢復客運專線在縱斷面上的平順性,實現客運專線縱斷面線形的重構。
5 結束語
在分析客運專線平面重構的基礎上,展開了針對縱斷面重構的探討,闡述了縱斷面線形重構的主要思路及方法,為縱斷面重構的相關研究提供一定的參考,為了滿足實際工程應用,后續工作中,還應開展約束條件如何影響重構結果的研究。

