單炮多發同時彈著的局部插值算法與并行加速

程李東,姜 毅,牛鈺森

(北京理工大學 宇航學院,北京 100081)

20世紀80年代后期,美國人機工程研究所針對野戰炮兵射擊提出了單炮多發同時彈著法(multiple round simultaneous impact,MRSI),通過調整火炮的發射裝藥和射角,使連續發射的多發炮彈同時擊中目標[1-3],其技術構想如圖1所示[2]。

目標受到火炮的首群炮彈打擊后會迅速采取規避或保護措施,如車輛機動、人員臥倒或進入掩體等,后續射擊對目標的毀傷概率大大降低。統計資料表明,暴露步兵遭受炮擊后2 s內有一半就地臥倒,8 s內全部轉為臥姿或隱蔽狀態,后續炮彈殺傷力將降低50%～80%[4]。采用MRSI射擊方法可在不增加火炮數量的條件下將首輪打擊的炮彈密集度增大數倍,大幅提升對目標的毀傷概率,進而提高炮兵部隊的作戰效率和生存能力。

MRSI射擊是現代火炮的發展趨勢,國外先進的自行加榴炮均具有同時彈著功能[5]。美國在1988～1993年間實現了AS90,M109A6等155 mm自行火炮的四彈同時彈著,同時測試和對比了標準裝藥模塊和液體裝藥的MRSI性能,1995年研究了先進牽引式火炮系統(ATCA)的MRSI性能,部分火炮的四彈MRSI可覆蓋其打擊范圍的85%[3]。2001年,陸欣等將MRSI的概念引進國內[2],祝軍利等給出了國內某型火炮在13～30 km射程范圍內的MRSI彈道分布[5],隨后李開龍、程恭等研究了MRSI射擊方法在大口徑艦炮上的應用,提出了彈道解算流程并分析了射擊效力[6-7],近年來相關研究逐漸轉向增程修正彈等新型可控炮彈[8-10]。

自動化火炮的火控系統擔負目標定位與跟蹤、氣象數據的測定和接收、射擊諸元的解算、瞄準與射擊控制等任務,其中射擊諸元的解算直接關系到打擊的速度和精度[11]。在機動作戰的條件下,戰場情形瞬息萬變,這對彈道計算機的解算速度提出了較高的要求,如裝備在我國69-II式坦克上的簡化輕型坦克火控系統要求彈道計算時間小于1 s[1]。現有的MRIS彈道算法[6-7]為滿足計算耗時的要求,均采用稀疏射擊序列計算,再結合線性插值的方式確定裝藥和射角。由于彈道方程具有非線性,稀疏序列插值將造成較大的彈道偏差。

為解決原有算法彈道偏差較大的問題,本文提出一種局部插值算法(local interpolation algorithm,LIA),并基于MPI編程模型實現多核并行計算,在大幅提升射角計算精度的同時滿足戰場對火控計算時間的要求。最后將研究結果應用于一定條件下5～15 km射程內的MRSI彈道計算,以檢驗算法的有效性和高效性。

1 數學模型

炮兵實際使用的彈道方程組是高維微分方程組,如美軍使用的修正質點彈道方程組[3,12],該彈道方程組考慮了地球自轉和彈體轉動帶來的影響。本文重點研究彈道算法和并行加速方法,因此僅以標準條件下二維質點彈道方程[4,13]為例,但研究結果可以直接應用于修正質點彈道方程、旋轉穩定炮彈彈道方程[14]、高空遠程彈箭精確彈道模型[15]等復雜彈道方程的解算。

1.1 標準條件下二維質點彈道方程

二維質點彈道方程考慮了空氣阻力,同時計及高度變化對大氣物理特性的影響：

虛溫τ按標準氣象條件計算,g=9.81 m/s2,ρ0,.N=1.206 kg/m3,d為榴彈彈徑,阻力系數cx0,N(Ma)由阻力定律確定,i為所選阻力定律下的彈形系數,m為彈體質量,p為大氣壓強。

1.2 真空二維彈道斜射程公式

真空彈道為拋物線彈道,不考慮空氣阻力,其射程總是大于同一裝藥在同一射角下的空氣彈道射程。根據外彈道學,真空彈道斜射程公式為[13]

式中:v0為炮口初速,α為瞄準角,ε為炮目高低角。

最大射程:

2 約束條件

2.1 射程重疊區間與裝藥分級

榴彈炮為達到射程要求,需要對發射裝藥進行一定的分級。從同時彈著射擊的角度來說,分級越多可實現同時彈著的彈道數量越多。但同時又必須盡可能簡化戰場操作,并考慮補給等問題,因此各級裝藥的射程重疊量通常為8%～12%,對于30 km射程的火炮,其裝藥常分為7級[4-5]。

2.2 最小發射時間間隔

2次射擊之間需要完成彈藥的再裝填、關閉艙門、重新瞄準等操作,且射擊之前需要保證炮身冷卻至容許溫度以下[16]。不同型號的火炮完成這些操作所需的時間不同,按常規火炮8 min-1的射速計算[5],2次射擊之間的最小時間間隔為Δtmin=8.75 s。這一間隔將作為彈道篩選的條件,即相鄰的2條同時彈著彈道的飛行時間差不小于Δtmin。

2.3 最小與最大射角

火炮的最小與最大射角受外彈道設計、火炮射界和炮身縱向傾角的共同限制,如圖2所示。

圖2中,OA與水平線平行,OB為目標視線,OC與炮臺平行;θ為火炮射角,φ為炮身縱向傾角,為射擊高低角。

一方面根據彈丸飛行動力學特性和跟隨性確定最大射高,進而確定理論最大射角θt,max[5]。另一方面,火炮射界受炮架結構的限制,射界越大炮架質量越大,榴彈炮的最小高低角γmin一般取-3°～-5°,最大高低角γmax可達70°甚至更大[1]。據此,實際火炮的射角范圍為

γmin+φ≤θ≤min{θt,max,γmax+φ}

2.4 命中精度

以人員殺傷為例,榴彈對人員的殺傷有2種方式:一是爆炸后飛散的破片造成人體組織穿透、斷離或撕裂,二是爆炸沖擊波對人體造成沖擊損傷[17]。2種殺傷方式的殺傷效果都隨爆炸距離的增大而迅速減小,前者是由于受空氣阻力影響,破片速度隨飛行距離增大而迅速減小,后者是由于沖擊壓力在空氣中迅速衰減。可對人員造成殺傷的最大爆炸距離即榴彈對人員的殺傷半徑。

由于彈道數學模型、陣地位置與高度測量、敵方距離和方位測量、氣象修正、初速修正以及數值求解過程中均存在誤差[18],實際采用MRSI方式射擊時一輪炮彈幾乎不可能同時到達目標點,最先和最后達到的炮彈的落地時差表征了MRSI彈道的時間精度。為保證殺傷效率,該時差應盡可能小。

3 局部插值算法

確定同時彈著射擊方案的思路是通過求解彈道方程組,選擇出覆蓋給定射程的裝藥,然后確定出各裝藥對給定射程的射角,最后根據限制條件得出射擊方案[2]。為滿足計算耗時的要求,已有文獻[6-7]的算法是給定一個較稀疏的離散射擊序列:

(v0,j,θj,I),j=1,2,…,M,I=0,1,2,…,Nj

式中:M為裝藥種數,Nj+1為第j號裝藥待計算的射角數量。求解該射擊序列對應的射程序列,再通過線性插值的方式確定可以命中目標的射擊序列:

(v0,j,θj,b),b=0,1,2,…,n

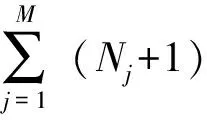
為克服上述算法彈道偏差較大的問題,可采用局部插值算法。對于第j號裝藥：

①根據真空彈道斜射程公式判斷其最大射程是否可以覆蓋目標；

②在火炮最大容許射角范圍[θmin,θmax]內采用二分法確定真空彈道達到或超過目標射程的射角范圍[θj,min,θj,max],θj,min和θj,max作為空氣彈道計算的射角下邊界和上邊界；

③給定某較小的射角增量Δθ,從θj,min開始向上逐個射角求解彈道。即給定(v0,j,θj,min+bΔθ),采用四階Runge-Kutta方法[19]求解彈道微分方程組,若存在命中目標(彈道落點與目標的距離不超過殺傷半徑)的彈道,則直接保存其彈道參數(v0,j,θj,min+bΔθ,tj,g)；若不存在命中目標的彈道,則計算直到第1條超過目標射程的彈道時停止向上遍歷,對最后2條彈道的參數做線性插值,得該裝藥對目標的低伸彈道；

④從θj,max開始向下逐個求解彈道,直到找到命中目標的彈道或第1條超過目標射程的彈道,結束對該裝藥的彈道求解,采用與③相同的方法得到該裝藥的曲射彈道；

⑤對全部裝藥求得的所有彈道按彈道飛行時間tj,i遞增排列,去除與前1條彈道的飛行時間差小于Δtmin的彈道,得到MRSI彈道的射擊序列。

記低伸彈道射角為θj,r,曲射彈道射角為θj,q,采用局部插值算法可將第j號裝藥求解的射角范圍限制于θj,use=[θj,min,θj,r]∪[θj,q,θj,max]。在本文第5節的計算條件下,第5號裝藥對10 km射程的θ5,use只占火炮容許射角范圍的4.58%,在計算量相當條件下可以將原有算法的稀疏彈道序列加密20倍左右。第7號裝藥在45 km附近的彈道偏差小于1 m,彈道計算精度得到了很大提升。第5號裝藥對10 km射程的邊界射角彈道曲線如圖3。θ5,use中包含61條彈道,與文獻[7]所給計算序列包含的射角數量51相差不大。

圖3中彈道曲線Ⅰ和Ⅱ為拋物線低伸和曲射彈道,射角分別為θj,min和θj,max；曲線Ⅲ～Ⅶ為空氣彈道,其中曲線Ⅲ和Ⅳ為低伸彈道,射角分別為θj,min和θj,r；曲線Ⅴ和Ⅵ為曲射彈道,射角分別為θj,max和θj,q；曲線Ⅶ為射角在[θj,r,θj,q]范圍內的彈道。

采用局部插值算法實現MRSI彈道計算的流程如圖4所示。

4 并行計算

在高性能并行計算中,基于消息傳遞的MPI(message passing interface)編程模型是科研和工程領域中的事實標準[20],本文采用MPI實現MRSI彈道的并行計算。在進行大量空氣彈道解算之前,需要先根據拋物彈道斜射程公式判斷各裝藥是否能達到目標射程,并確定可達到目標射程的裝藥的空氣彈道上、下邊界,所有裝藥的空氣彈道計算結束后需要對命中目標的彈道排序、篩選以確定MRSI彈道射擊序列,以上任務計算量較小,單個CPU便可迅速完成；大量空氣彈道的解算則由多個CPU并行完成。因此本文采用MPI模型中的1?N集合通信模型[21],在所有參與計算的CPU中,存在一個Host(主CPU),負責數據前處理、任務分配和最終的彈道序列生成；其余均為Device(設備CPU),只負責大量空氣彈道的并行解算。本文研究所用計算平臺的CPU為6核12線程,型號為Intel(R)Core(TM)i7-5820k,主頻3.30 GHz；內存32 GB；操作系統為Windows Server 2012R2 Standard。

4.1 任務分配方案

為確定MRSI射擊序列,需對局部插值算法確定的射角范圍內的密集彈道序列進行解算,為此可有以下3種任務分配方案供選擇(設有k個Device)。

① 每個Device負責一種裝藥的彈道解算,M種裝藥需要k=M；

② 依次計算各裝藥的彈道,每個裝藥的θj,use被均分為k段,每個Device計算其中一段；

③ 依次計算各裝藥的彈道,各Device計算的彈道按插空分配,設裝藥j需要計算的射角序列為

[θj,0,θj,1,θj,2,…,θj,Nj]

則第h個Device負責計算的射角序列為

[θj,h,θj,h+k,θj,h+2k,…,θj,h+fk],h+fk≤Nj

式中:f為滿足h+fk≤Nj的最大自然數。

方案①為粗粒度并行,方案②和方案③為細粒度并行。為減少計算耗時,需要盡可能提高并行算法的并行度。由于各裝藥的炮彈初速差別較大,θj,use占火炮最大容許射角范圍的比例相差也會較大,所以按照方案①分配時,各Device的計算量明顯不均勻,算法的并行度較低。根據外彈道學,曲射彈道的彈道飛行時間總是大于低伸彈道。按方案②分配計算任務時,由于各Device求解彈道方程的時間步長為統一值,曲射彈道的時間步數量總會大于低伸彈道,算法并行度低。按方案③分配任務時,由于同一裝藥相鄰射角的彈道差別不大,各Device之間可實現最大程度的并行。綜合上述分析,任務分配應采用方案③。

圖5為采用不同的任務分配方案計算10 km射程的MRSI彈道所消耗的計算時間,數值實驗結果與上述分析相吻合。計算耗時為tc,計算中保證Device數量k=M,其余計算條件見第5節。

4.2 并行效率

由圖6可知,隨著Device數量的增加,并行效率在遞增,但遞增的速度減緩。這是由于隨著Device數量的增加,彈道計算所消耗的時間減少,數據處理消耗的時間占總耗時的比重上升,且用于通信和數據處理的時間消耗會增加。由此可以預測,存在某個Device數Mη使得并行效率取最大值,之后再增加Device的數量,并行效率將降低,實際系統的Mη可由實驗確定。從并行效率、硬件復雜程度、可靠性和經濟性等角度考慮,彈道計算機的Device數量不應該超過Mη。

5 應用實例

為驗證局部插值算法和并行算法的有效性,取如下條件做MRSI彈道仿真計算。

①榴彈彈徑d=122 mm,cx0,N(Ma)采用43年阻力定律,彈形系數i=1.035；

②各級裝藥的炮彈初速如表1所示。

表1 裝藥初速表

③兩次射擊之間的最小時間間隔Δtmin=8.75 s；

④火炮最大容許射角范圍為5°～85°；

⑤命中精度：榴彈殺傷半徑為10 m,MRSI彈道時間精度為0,即計算狀態下所有炮彈同時落在距離目標10 m以內；

⑥射程范圍5～15 km,計算間隔為1 km,目標相對我方陣地高度為100 m；

⑦Δθ=0.06°,Runge-Kutta法求解彈道方程時,為保證彈道計算精度,時間步長取1 ms。

計算結果：15 km射程計算耗時最大,為14.16 s,與文獻[2]相符,所得MRSI彈道數量Q隨射程X的分布如圖7。文獻[3]的彈道數量分布在2～6條,與本文相符。

圖7中,10 km射程的MRSI彈道射擊序列見表2,j為裝藥號,θ為射角,t為彈道飛行時間,ts為射擊時刻。

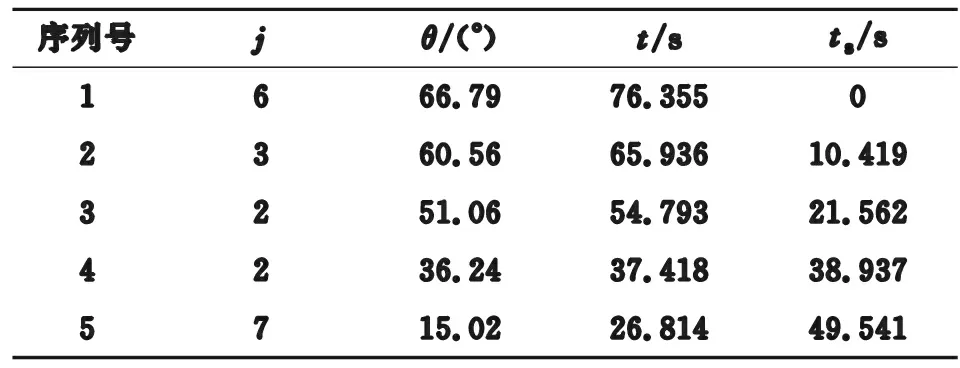
表2 10 km射程MRSI彈道射擊序列

10 km射程的MRSI彈道曲線如圖8,其中編號Ⅰ～Ⅴ對應表2中的序列號1～5.

6 結論

本文分析了已有的MRSI彈道算法和彈道分布規律,在此基礎上做了以下研究工作：

①提出了一種局部插值算法,可大幅提高彈道計算精度,同時引入MPI并行計算,保證計算耗時滿足戰場要求；

②在并行算法設計中,分析了不同任務分配方式的并行度,結合數值實驗結果,選擇并行度最高的第③方案；

③根據并行效率與CPU核心數量的關系,指出彈道計算機的CPU數量不應該超過Mη；

④應用局部插值算法結合并行計算,在一定條件下計算了5～15 km射程的MRSI彈道,驗證了算法的有效性和高效性。

雖然本文的研究對象只是普通自動化榴彈炮,但局部插值算法和并行計算方法可直接推廣到基于瞄準點排布的面積殺傷法[7]和一維修正彈[8-10]的MRSI彈道計算中。近年來,通用圖形處理器(general purpose graphics processing units,GPGPU)并行加速技術已經在計算傳熱學[22]、計算流體力學[23]以及信號處理[24]等多個領域取得了應用。相比于CPU,GPGPU更適合于進行大規模重復性計算,未來可以考慮將GPGPU并行加速應用于MRSI彈道求解,以解決更復雜的新型可控炮彈[25]MRSI彈道解算問題。

[1] 談樂斌,張相炎,管紅根,等. 火炮概論[M]. 北京:北京理工大學出版社,2005.

TAN Lebin,ZHANG Xiangyan,GUAN Honggen,et al. Introduction to artillery[M]. Beijing:Beijing Institute of Technology Press,2005.

[2] 陸欣,周彥煌. 單炮多發同時彈著的數學模型和數值分析[J]. 火炮發射與控制學報,2001(3):5-6,27.

LU Xin,ZHOU Yanhuang. Mathematic model and numerical simulation of single gun multiple round time-on-target technology[J]. Gun Launch & Control Journal,2001(3):5-6,27. (in Chinese)

[3] KOGLER T M. Single gun,multiple round,time-on-target capability for advanced towed cannon artillery[R]. Maryland:Army Research Lab Aberdeen Proving Ground,1995.

[4] 謝黎焱,廖瑞,王雪琴. 信息化條件下單炮多發同時彈著研究[J]. 指揮控制與仿真,2009,31(4):30-32,36.

XIE Liyan,LIAO Rui,WANG Xueqin. Study on single cannon multiple round time-on-target under informationizated condition[J]. Command Control & Simulation,2009,31(4):30-32,36. (in Chinese)

[5] 祝軍利,高效生,侯曉峰. 自行加榴炮多發同時彈著技術[J]. 火炮發射與控制學報,2005(1):6-8.

ZHU Junli,GAO Xiaosheng,HOU Xiaofeng. Technique of MRSI of self-propelled cannon/howitzer[J]. Gun Launch & Control Journal,2005(1):6-8. (in Chinese)

[6] 李開龍,石章松,龔馳,等. 大口徑艦炮多發同時彈著射擊效力分析[J]. 艦船電子工程,2011,31(9):31-33,42.

LI Kailong,SHI Zhangsong,GONG Chi,et al. Analysis of time-on-target fire effectiveness of large caliber naval gun[J]. Ship Electronic Engineering,2011,31(9):31-33,42. (in Chinese)

[7] 程恭,石章松,王航宇. 基于瞄準點排布模型的多發同時彈著射擊諸元解算[J]. 艦船電子工程,2011,31(11):29-32,42.

CHENG gong,SHI Zhangsong,WANG Hangyu. Firing data solutions for multiple rounds simultaneous impact based on aiming point distribution model[J]. Ship Electronic Engineering,2011,31(11):31-33,42. (in Chinese)

[8] 黃義,汪德虎,汪匯川,等. 艦炮發射一維修正彈多發同時彈著研究[J]. 彈箭與制導學報,2012,32(5):127-129.

HUANG Yi,WANG Dehu,WANG Huichuan,et al. The research on MRSI of one-dimensional trajectory correction projectile fired by shipborne gun[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(5):127-129.(in Chinese)

[9] 劉劍威,王海川. 增程修正彈單炮多發同時彈著火控技術研究[J]. 指揮控制與仿真,2012,43(1):70-72,77.

LIU Jianwei,WANG Haichuan. Research on method of multiple rounds simultaneous impact of extended range and trajectory correction projectile[J]. Command Control & Simulation,2012,43(1):70-72,77. (in Chinese)

[10] 石章松,傅冰,胡獻君,等. 基于增程修正彈的同時彈著火控機理[J]. 海軍工程大學學報,2013,25(3):7-12.

SHI Zhangsong,FU Bing,HU Xianjun,et al. Time-on-target fire control mechanism based on extended-range trajectory correction projectile[J]. Journal of Naval University of Engineering,2013,25(3):7-12. (in Chinese)

[11] 孟燦,毛征,孟博,等. 彈丸飛行時間與射擊諸元關系分析[J]. 兵工自動化,2016,35(11):24-27.

MENG Can,MAO Zheng,MENG Bo,et al. Analysis on relation of projectile flight time and firing data[J]. Ordnance Industry Automation,2016,35(11):24-27. (in Chinese)

[12] LIESKE R F,REITER M L. Equations of motion for a modified point mass trajectory[R]. Maryland:Army Ballistic Research Lab Aberdeen Proving Ground,1966.

[13] 韓子鵬. 彈箭外彈道學[M]. 北京:北京理工大學出版社,2008:72-77.

HAN Zipeng. Exterior ballistics of rockets and missiles[M]. Beijing:Beijing Institute of Technology Press,2008:72-77. (in Chinese)

[14] 錢明偉,王良明,郭錫福. 火炮武器高原射擊時的彈道特性研究[J]. 彈道學報,2009,21(4):21-25.

QIAN Mingwei,WANG Liangming,GUO Xifu. Ballistic analysis for artillery systems firing on plateau[J]. Journal of Ballistics,2009,21(4):21-25. (in Chinese)

[15] 李臣明,舒敬榮. 高空遠程彈箭精確彈道模型[J]. 彈道學報,2008,20(4):8-11.

LI Chenming,SHU Jingrong. Precise exterior ballistic model for long-range missile versus high altitude[J]. Journal of Ballistics,2008,20(4):8-11. (in Chinese)

[16] 朱文芳,王育維,郭映華,等 某火炮身管溫度仿真計算及其影響因素分析[J]. 火炮發射與控制學報,2016,37(4):58-62.

ZHU Wenfang,WANG Yuwei,GUO Yinghua,et al. Temperature simulation calculation and analysis of influential factors of a certain gun barrel[J]. Journal of Launch & Control,2016,37(4):58-62. (in Chinese)

[17] 王志軍,尹建平. 彈藥學[M]. 北京:北京理工大學出版社,2005:106-116.

WANG Zhijun,YIN Jianping. Ammunition[M]. Beijing:Beijing Institute of Technology Press,2005:106-116. (in Chinese)

[18] 武瑞文,王兆勝. 自行火炮武器系統射擊精度研究[J]. 兵工學報,2004,25(4):407-409.

WU Ruiwen,WANG Zhaosheng. A study on the firing accuracy of self-propelled artillery systems[J]. Acta Armamentarii,2004,25(4):407-409. (in Chinese)

[19] BURDEN R L,FAIRES J D. Numerical analysis[M]. Boston,Massachusetts:Brooks/Cole,2011:282-291.

[20] 龔春葉,包為民,湯國建,等. 航天領域高性能并行計算研究進展[J]. 計算機工程與科學,2014,36(9):1629-1636.

GONG Chunye,BAO Weimin,TANG Jianguo,et al. Recent progress in high-performance parallel computing of the aerospace aera[J]. Computer Engineering & Science,2014,36(9):1629-1636. (in Chinese)

[21] 張武生,薛巍,李建江,等. MPI并行程序設計實例教程[M]. 北京:清華大學出版社,2009:152-157.

ZHANG Wusheng,XUE Wei,LI Jianjiang,et al. Examples of MPI parallel programming[M]. Beijing:Tsinghua University Press,2009:152-157. (in Chinese)

[22] OUYANG A,TANG Z,ZHOU X,et al. Parallel hybrid PSO with CUDA for lD heat conduction equation[J]. Computers & Fluids,2015,110:198-210.

[23] PICKERING B P,JACKSON C W,SCOGLAND T R W,et al. Directive-based GPU programming for computational fluid dynamics[J]. Computers & Fluids,2015,114:242-253.

[24] LOBEIRAS J,AMOR M,DOALLO R. BPLG:a tuned butterfly processing library for GPU architectures[J]. International Journal of Parallel Programming,2015,43(6):1078-1102.

[25] 克里斯托弗·福斯,庫宗波. 智能彈藥:野戰炮兵精確制導彈藥[J]. 國外坦克,2016(10):20-26,31.

FUSS C,KU Zongbo. Intelligent munition:precision-guided munitions of field artillery[J]. Foreign Tanks,2016(10):20-26,31. (in Chinese)