考慮距離因素的多方式交通超級網絡均衡配流模型及算法

周豪，四兵鋒，汪勤政

(北京交通大學交通運輸學院，北京 100044)

經濟的快速發展和城市化進程的不斷推進，使得居民出行距離不斷增加，供出行者選擇的交通方式也越來越多。不同方式在不同距離范圍內有著不同優勢，例如，自行車適合較短距離出行，小汽車適合較長距離出行，而電動汽車因為受到電量約束，出行距離具有上限。因此，出行距離是影響出行者方式選擇的重要因素。此外，隨著出行距離的增加，出行者所花費的出行成本也會相應上升，因此，距離因素也會影響出行者的路徑選擇。在多方式交通系統中，出行者的選擇行為會直接決定其出行活動，所有出行活動的聚集現象則形成了網絡流量狀態。因此，研究考慮距離因素的出行者選擇行為及在此基礎上的多方式交通配流問題對于現代綜合交通管理具有重要的現實意義。

自Wardrop在1952年提出了“用戶平衡條件”的概念，尤其是Beckmann在1956年提出與之等價的數學模型后，基于用戶平衡思想的交通配流理論得到了快速發展。然而，大部分研究是針對單一模式的交通網絡展開的。例如，城市公交網絡客流分配[1]、城市軌道交通網絡客流分配[2]等。目前，有些學者開始關注多方式交通網絡的配流問題，例如，Wu等[3]考慮了步行和公交兩種方式，建立了一個分層網絡模型，并提出了多方式網絡平衡配流模型；黃海軍等[4]研究了組合出行方式下的混合均衡分配問題，提出了與用戶均衡條件等價的變分不等式模型；四兵鋒等[5]提出了一種分層網絡結構來描述多方式交通網絡，并提出了考慮不同方式之間相互干擾的變分不等式模型；汪勤政等[6]構建了多方式交通系統的可換乘超網絡模型，考慮出行者的出行規律、出行行為和換乘等條件，基于圖的遍歷算法和Dijkstra算法，提出了超網絡有效超路徑的搜索算法和最短有效超路徑算法。近年來，隨著電動汽車等新能源交通工具的發展，有些學者開始關注考慮路徑約束的網絡配流問題。例如，Kang等[7]采用基于活動的方法，對出行者的充電路徑選擇進行了研究；He等[8]考慮了電動汽車單一模式交通網絡，提出了基于出行距離約束下的用戶平衡配流模型。然而，在該研究中，所建立的廣義費用函數均沒有考慮距離因素對出行者選擇行為的影響，路徑約束條件只是針對電動汽車單一模式，沒有考慮多方式組合出行條件下距離因素對出行行為的影響。

在以往的研究中沒有考慮出行距離對出行者廣義費用和出行選擇的影響，且只考慮對單一方式進行路徑約束，沒有綜合考慮出行者在整個多方式交通系統中的出行選擇行為。本文針對多方式交通網絡的流量分配問題展開研究，綜合考慮距離因素對出行者的方式選擇和路徑選擇，特別深入分析了距離因素對出行者廣義感知費用的影響，定義了超路徑，提出了最短超路徑搜索算法。并提出了考慮距離因素的多方式交通網絡均衡流量分配模型及算法。最后，通過一個簡單算例對模型及算法進行了驗證分析。

1 多方式交通超級網絡模型

在多方式交通網絡中，出行者完成一次出行往往需要經歷4個階段：從出行起點行走或行駛到達某一網絡節點，即上網過程；采用某種交通方式行駛到達換乘節點，即運行過程；在換乘節點從一種交通方式步行換乘到另一種交通方式，即換乘過程；從目的網絡節點行走或行駛到達最終的出行終點，即下網過程。根據出行者的出行特征，本文采用超網絡結構來描述多方式交通系統。在多方式超級交通網絡中，每種交通方式都有自己的運行子網，不同交通子網之間通過換乘節點進行連接。多方式超級交通網絡可描述為：

G=(M,V,A)，

(1)

其中，G表示多方式超級網絡；M表示交通方式集合；V表示交通節點集合；A表示各類弧的集合。

在多方式超級網絡中，根據節點和弧的不同屬性，可將其分為不同的類別，不同類別的節點和弧可通過不同的狀態向量進行描述。節點可分為出行端點和非出行端點，出行端點表示一次出行的起點或終點，這類節點集合用V1來表示，其中的元素用單變量r或s表示，即r,s∈V1；而非出行端點表示出行過程中的中間節點，這類節點集合用V2來表示，其中的元素用二維向量(m,v)表示，即(m,v)∈V2，m和v分別表示節點的交通方式屬性和位置屬性。在多方式超級網絡中，弧可以分為上網弧、運行弧、換乘弧和下網弧等四類，不同類型的弧的集合分別用A1、A2、A3、A4表示，即：

A=A1∪A2∪A3∪A4，

(2)

可用所連接的兩個相鄰節點來表示一條弧，例如上網弧可表示為{r,(m,v)}，運行弧可表示為{(m,v1),(m,v2)}，換乘弧可表示為{(m1,v),(m2,v)}，而下網弧可表示為{(m,v),s}。

在多方式超級網絡中，出行者從起點到終點完成一次出行，需要經歷上網、乘車、換乘、下網等一系列出行活動，這些活動可通過超網中具有序列關系的點或弧進行描述。

在此，本文提出超路徑的概念來描述出行過程，定義：超路徑是指在多方式超級網絡中由起點到終點有連接關系的多方式交通網絡節點所組成的序列。例如，從起點r到終點s的一條超路徑可表示為：

r→(m1,v1)→(m1,v2)→…→(m1,vn)→(m2,vn)→…→(mn,vw)→s

(3)

在實際出行中，出行者不會考慮起點到終點之間所有連通的超路徑，因此，需要對超路徑進行限定，本文將滿足下述條件的超路徑定義為有效超路徑，并假定出行者進行出行選擇時僅考慮有效超路徑，將r-s之間的有效超路徑所組成的集合記為Krs：

(1)換乘次數不超過一個給定的最大值nmax；

(2)不存在連續換乘弧；

(3)不包含回路；

在一條有效超路徑中，通常會包括多段連續運行弧，也就是說，出行者在進行換乘之前，會在某一種交通子網中出行一段距離，然后在適當的換乘點轉換到另外一種交通子網中。本文定義子路徑為：在多方式超級網絡的一條有效超路徑中，相鄰的上網弧、換乘弧和下網弧之間的運行弧序列。顯然，有效超級路徑可以看成是由上網弧、子路徑、換乘弧以及下網弧所組成的。例如，在式(3)表示的超路徑中，以下節點序列則構成了該超路徑的一條子路徑。

(m1,v1)→(m1,v2)→…→(m1,vn)。

(4)

圖1給出了一個簡單的多方式超級網絡，在這個超網中包含4個子網，分別為小汽車子網(c)、電動車子網(e)、自行車子網(b)和公交車子網(p)。

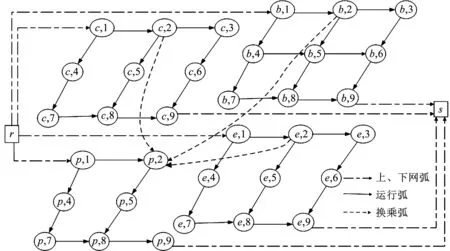
圖1 多方式超級網絡Fig 1 The multimodal super network

圖1中，r→(b,1)→(b,2)→(p,2)→(p,5)→(p,8)→(p,9)→s就是該超網絡中的一條有效超路徑，該有效超路徑中包含了自行車和公交兩種方式的子路徑。(p,2)→(p,5)→(p,8)→(p,9)是其中的一條公交車子路徑。

2 考慮距離因素的出行廣義費用

在多方式交通網絡中，出行者在出行中既要選擇交通工具，還要選擇出行線路，影響出行者選擇的因素有很多，包括時間、花費、換乘、舒適度等。在以前的研究中，很少考慮距離因素對出行者交通選擇的影響，然而，距離因素是影響出行者交通選擇，尤其是方式選擇的重要因素。例如，隨著距離的增加，出行花費會增加，舒適度會下降，且不同方式對于距離的敏感性也是不同的。

根據以上分析，出行者的出行過程包括上網、車輛運行、換乘及下網4個過程。相應的，出行者在這些過程中所承擔的費用可用這些弧段上的費用來表示。超路徑費用由上網費用、子路徑費用、換乘費用和下網費用組成，其中上網費用、換乘費用和下網費用均為常數，是對時間費用的適當放大；而子路徑費用可以由運行弧費用求得。

首先，構建上、下網弧以及換乘弧的廣義費用。而子路徑費用可以由運行弧費用求得，包括時間費用和價格費用。其中，時間廣義費用通過對子路徑的運行時間適當放大得到，放大因素包括道路擁擠、公交車車內擁擠以及距離增加帶來的舒適度損耗成本；而子路徑的價格費用則是距離的單調遞增函數。

根據以上分析，對各弧段的廣義費用進行分析和建模。

(1)上網弧和下網弧的廣義費用

上網弧費用是指出行者從出行起點到達相鄰網絡節點所花費的時間，而下網弧費用則表示出行者從最后的網絡節點到出行終點所花費的時間。通常，這兩類弧上的費用可以假定為常數，即：

(5)

(6)

(2)換乘弧廣義費用

換乘弧的費用是指換乘時間，由步行時間和等待時間組成，本文假定換乘時間為常數。由于換乘通常需要消耗體力，因此，換乘時間所產生的出行者心理感知費用是對換乘時間的適度放大。節點(m1,v)到(m2,v)間的換乘費用可表示為：

(7)

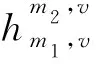
(3)子路徑廣義費用

根據前面的定義，子路徑是由同一方式的運行弧組成的，子路徑上的費用表示出行者在某一方式子網內出行一段距離所承擔的費用。通常，影響出行者出行選擇的因素包括時間、價格、舒適度等，其中時間因素就是車輛的行駛時間，價格因素包括票價、油耗等，而舒適度則是指車輛內部擁擠所產生的心理費用。在實際的出行過程中，價格因素和舒適度因素均和車輛行駛距離有關，例如，交通價格(或者油耗)一般會隨著距離的增加而增加，而車內的舒適度會隨著出行距離的增加而下降，并且不同方式的廣義費用隨距離變化的趨勢也是不同的。

首先，在多方式超級網絡中，方式m的車輛在運行弧上的行駛時間可表示為路段流量的單調增函數，如果考慮不同方式車輛之間的相互干擾，可采用式(8)所示的函數形式進行計算[9]：

(8)

由于不同方式車輛的平均載客人數不同，因此，選擇不同交通方式的出行需求所形成的道路流量是不同的，可采用下式計算不同方式車輛的道路流量[9]：

(9)

此外，出行者乘坐車輛行駛過程中，除了出行時間的之外，還需要承擔由車內擁擠所帶來的舒適性成本，尤其對于公交出行而言。因此，將方式m的出行時間放大，表示舒適度對于出行的影響，如式(10)所示。

(10)

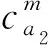
同時，隨著出行距離的增加，由時間和舒適度所產生的費用會逐漸放大，并且不同交通方式對距離的敏感性是不同的。因此，某一超路徑k上子路徑lk上的出行時間和舒適度成本如式(11)所示。

(11)

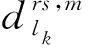
(12)

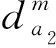
(13)

其中，am和bm表示與不同方式相關的待定參數。

在子路徑費用中，除了時間和舒適度的心理感知費用外，影響出行者交通行為的因素還有價格因素。對于小汽車來說，這部分費用包括油耗、過路費等，對于公交而言，則為票價。通常，價格費用與出行距離直接相關，距離越長，所花費價格越高。可以用式(14)來表示OD對r-s之間方式為m的有效超路徑k上子路徑lk的價格費用：

(14)

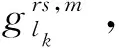
(15)

式中,τ為待定參數。

(16)

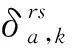
(17)

以路段流量為變量，超路徑的廣義費用可表示成如下形式：

(18)

3 多方式交通網絡均衡配流模型

本文采用用戶平衡(user equilibrium，UE)準則對網絡中的流量進行分配，該準則也被稱為Wardrop平衡原則。當交通網絡的流量分配達到平衡時，在OD對r-s之間的所有有效超路徑中，出行者所采用的各條路徑上的廣義費用均相等，且不大于未被使用路徑上的出行費用。其費用和流量有如下關系：

(19)

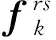
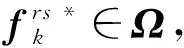
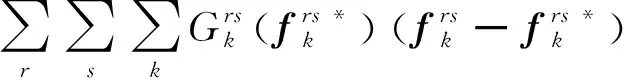
(20)

其中：

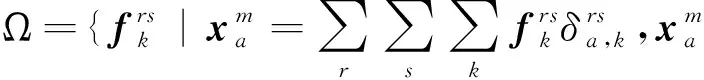
r,s∈V1,k∈Krs,a∈A,m∈M}。

(21)

4 求解算法

本文采用連續平均算法(MSA算法)求解該UE平衡配流問題[10]，具體步驟如下：

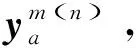
Step4:迭代更新，計算：

(22)

Step5:收斂性檢查。如果滿足

(23)

算法結束；否則，令n=n+1，轉Step2。

在求解本文的UE問題時，需要確定最短有效超路徑，傳統的最短路徑搜索算法對本文所考慮的子路徑問題無法描述，因此本文基于Dijkstra算法，提出考慮子路徑的超網絡最短有效超路徑搜索算法，具體步驟如下：

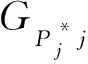
Step2：取Ci中的某一節點，如j：

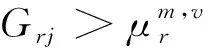
(2)若弧(i,j)∈A2，判斷：

b)若弧m(i,j)=0，轉Step3；

(3)若(i,j)∈A3，判斷弧(pi,i)∈A3是否成立，是，則轉step6；否，轉Step4；

Step4：令n(r,j)=n(r,i)+1，判斷n(r,j)?nmax是否成立，是,轉step5；否，則轉Step6；

Step6: 將j從集合Ci中移除, 判斷Ci是否為空，是，轉入Step7；否，轉入Step2；

Step7:找出標號為0的點中費用最小的點，如j，令s(j)=1,并將j設為當前節點，令K=K+1，轉Step8；

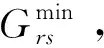
5 算例分析

以圖1所示的多模式交通網絡為例對說明模型及算法進行驗證，對文中參數作如下取值：

(1)η=1.1，ε=0.001，τ=0.2；

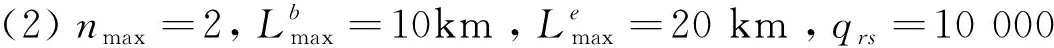
各交通方式相關信息如表1～表3所示：

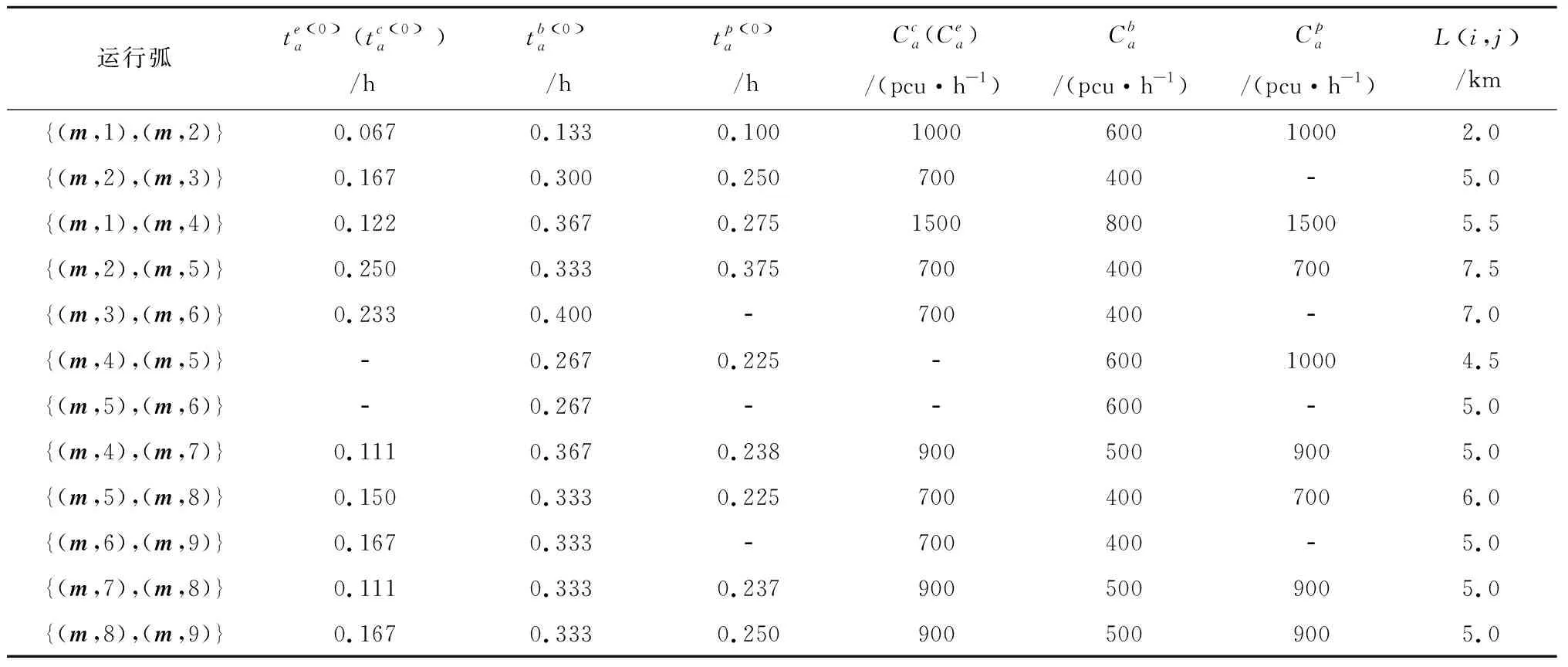
表1 弧段的相關信息

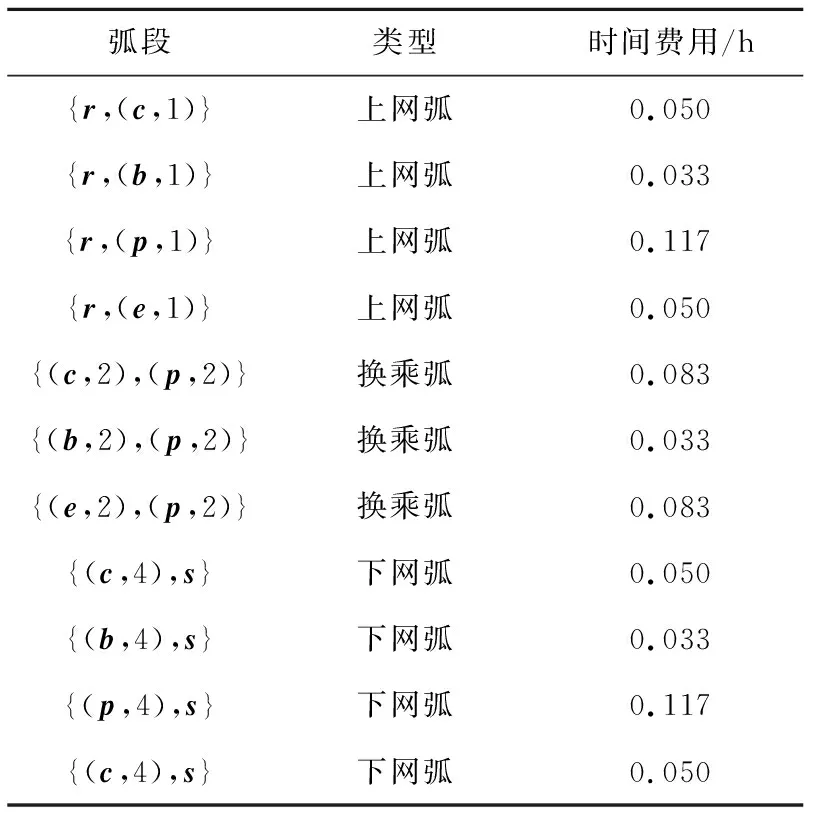
表2 上、下網弧及換乘弧相關數據

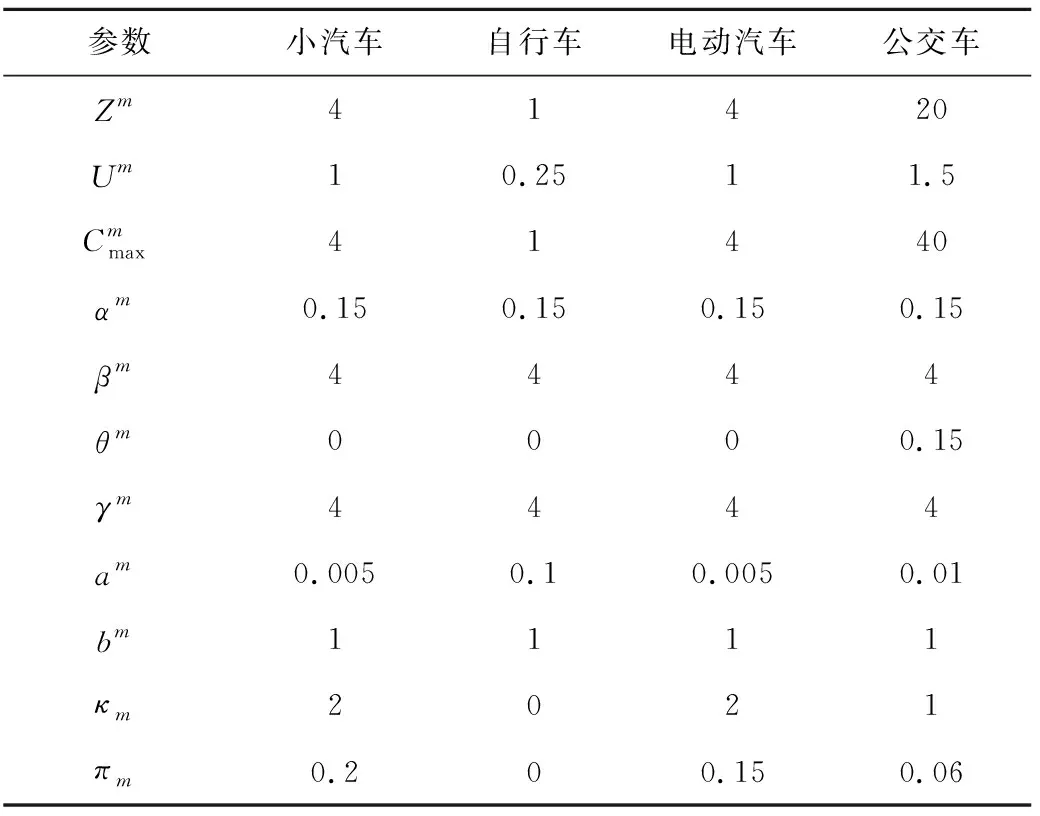
表3 交通模式的相關數據

首先分析MSA算法的收斂性，通過每次迭代中弧段{(c,1),(c,2)} 上小汽車和{(e,1),(e,2)}上電動汽車出行需求的變化來表示算法的收斂性。圖2給出了MSA算法的前30次的計算結果。可以看出，MSA算法具有明顯的收斂性質。

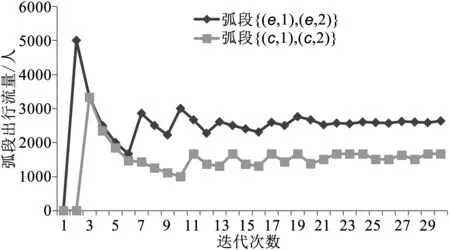
圖2 交通需求隨迭代次數的變化Fig.2 Variations of demands of car and electric car vs iteration times

用MATLAB對算例進行求解，首先對網絡中的參數賦值，求得各弧段以及子路徑的費用，用第4部分中的最短超路徑搜索算法尋找最短路徑。對最短路徑采用全有全無配流，得到附加交通流，并更新各弧段的流量。重復以上過程，直至達到網絡平衡的收斂條件。本文中的簡單算例，共有18條超路徑，經程序計算，當網絡達到平衡狀態時，超網絡中的有效超路徑一共有5條，每條路徑的出行模式如表4所示。當達到平衡狀態時，根據本文算法得到的各弧段上的交通需求如圖3所示。

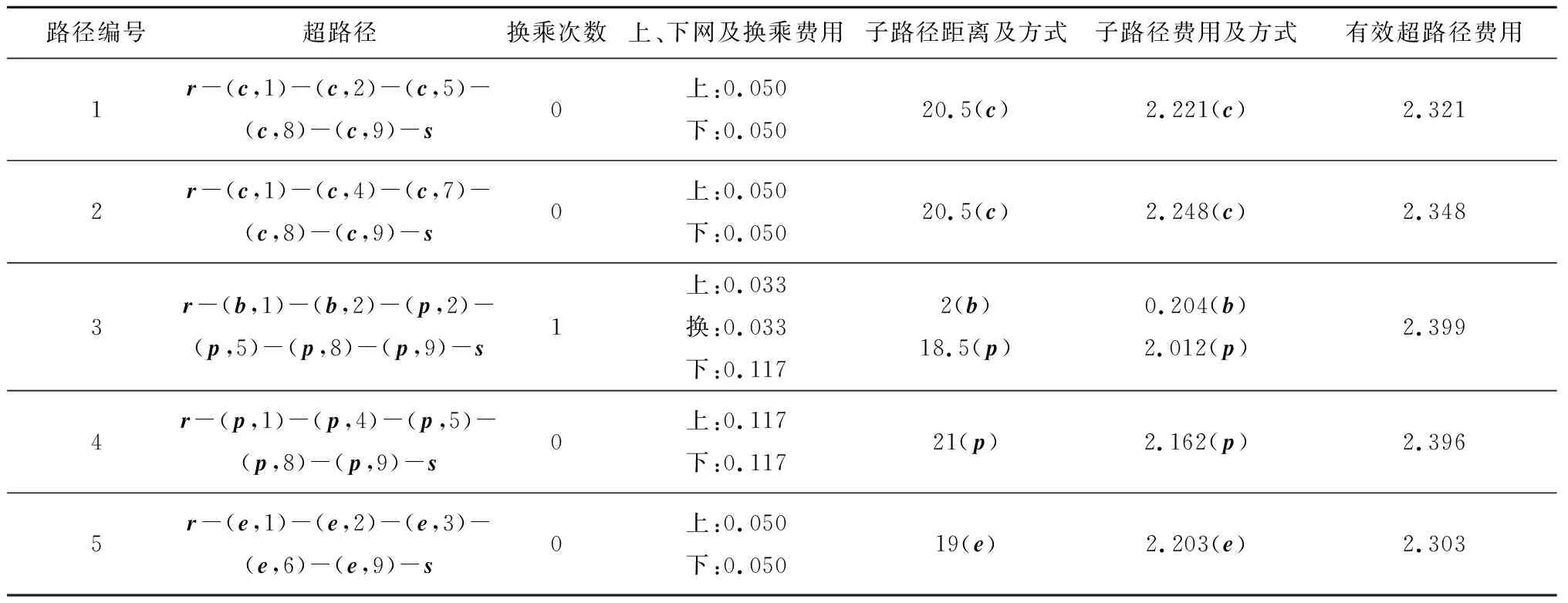
表4 有效超路徑分配結果

從圖3的配流結果中可以看出，在有電動汽車行駛的路段上(例如路段{(m,2),(m,3)})，小汽車的流量均為0，這是因為相同路徑上電動汽車的廣義費用比小汽車低，因此出行者會全部選擇電動汽車。但是當路徑的距離超出電量限制時，例如超路徑r-(e,1)-(e,4)-(e,7)- (e,8)-(e,9)-s，出行者便不能選擇電動車出行。自行車流量只分布在路段{(b,1),(b,2)}上，其他路段上自行車的流量為0。這是因為自行車只適宜在較短的距離內出行，當距離較長時，自行車將消耗較大的人力，出行者便不會選擇，為了發揮自行車短距離出行的優勢，自行車通常在多方式組合出行中采用。選擇單模式的出行量占90.75%，選擇多方式組合的出行量占9.25%，這是因為多方式換乘的費用較高，導致出行廣義費用增加，因此選擇多方式組合出行的流量較少。

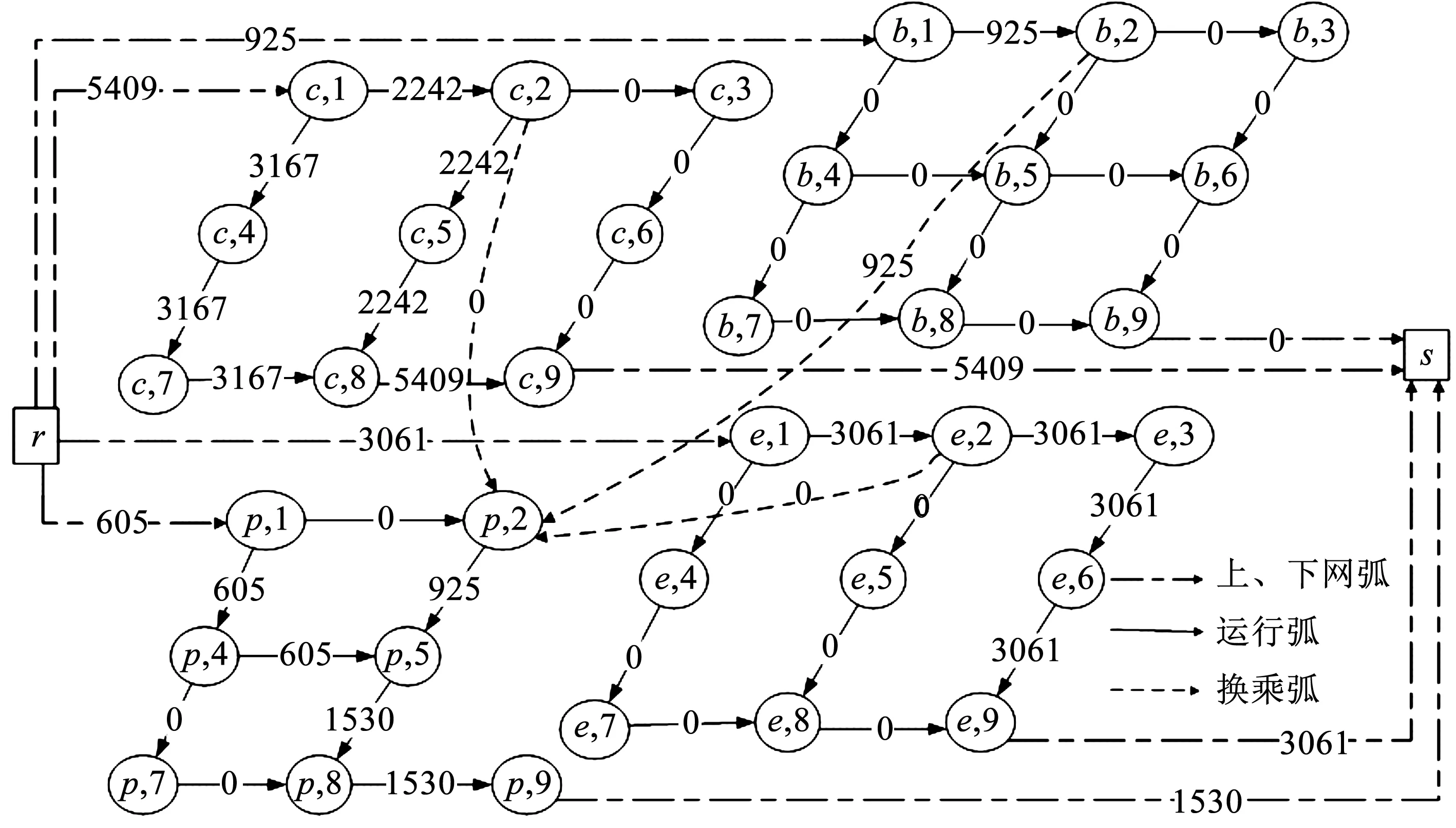
圖3 平衡時超網絡的路段流量Fig 3 The link flow of super network at equilibrium

6 結語

本文基于圖論方法建立了用于描述多方式組合出行的超網絡模型，驗證結果表明本文提出的模型和算法是有效的，并且說明了距離是影響出行者方式選擇和路徑選擇的重要因素。距離既影響時間，又影響價格，無論是對出行者的路徑選擇或方式選擇都有著重要的影響，考慮距離因素更符合出行者的實際出行選擇。通過算例說明了距離對出行選擇的影響，例如出行者僅在短距離出行中會選擇自行車，而長距離中選擇其他交通工具，這一結果是與實際相符的。

參考文獻：

[1]楊新苗, 馬文騰. 基于GIS的公交乘客出行路徑選擇模型[J]. 東南大學學報(自然科學版), 2000, 30(6):87-91.

[2]SI B F, ZHONG M, LIU J F, et al. Development of a transfer-cost-based logit assignment model for the Beijing rail transit network using automated fare collection data[J]. Journal of Advanced Transportation, 2013; 47(3):297-318.

[3]WU Z, LAM W. A network equilibrium model for congested multi-mode transport network with elastic demand[C]// Proc. 7th Conf. Hong Kong Society for Transportation Studies,Hong Kong,2002:274-283.

[4]黃海軍, 李志純. 組合出行方式下的混合均衡分配模型及求解算法[J]. 系統科學與數學, 2006, 26(3):352-361.

[5]四兵鋒, 楊小寶, 高亮,等. 基于出行需求的城市多模式交通配流模型[J]. 中國公路學報, 2010, 23(6):85-91.

[6]汪勤政, 四兵鋒. 換乘約束下城市多方式交通分配模型與算法[J]. 交通運輸系統工程與信息, 2017, 17(4):159-165.

[7]KANG J, RECKER W. An activity-based assessment of the potential impacts of plug-in hybrid electric vehicles on energy and emissions using 1-day travel data[J]. Transportation Research Part D Transport & Environment, 2009, 14(8):541-556.

[8]HE F, YIN Y, LAWPHONGPANICH S. Network equilibrium models with battery electric vehicles[J]. Transportation Research Part B Methodological, 2014, 67(3):306-319.

[9]四兵鋒,鐘鳴,高自友.城市混合交通條件下路段阻抗函數的研究[J]. 交通運輸系統工程與信息, 2008, 8(1):68-73.

[10]四兵鋒,高自友.交通運輸網絡流量分析與優化建模[M]. 北京：人民交通出版社, 2013.