基于組合近似模型的GCHE連桿結構優化設計
徐方超,張洪信,趙清海,徐東,王東
(青島大學 a. 機電工程學院; b. 動力集成及儲能系統工程技術中心,山東 青島 266071)
0 引言
傳統內燃機布局復雜、消耗大量化石能源、環境污染嚴重等缺點嚴重阻礙其發展。能源緊張問題使得新型發動機的研究越來越多,缸間齒輪聯動液壓發動機(gear-linked cylinders hydraulic engine,GCHE)便是其中一種。GCHE剛性動力傳輸,它能將熱能轉化為流體的壓力能,工作效率更高,運行更加平穩,缸間齒輪齒條無側隙嚙合傳動[1],其結構原理如圖1所示。
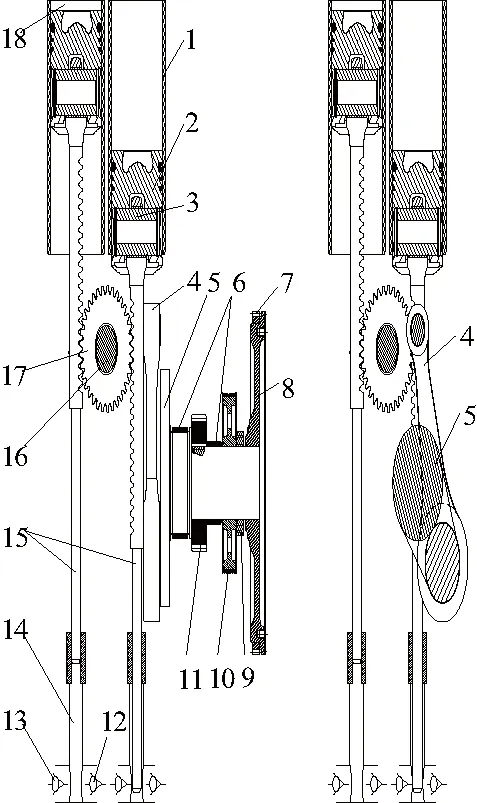
1—缸套;2—活塞;3—活塞銷;4—連桿;5—曲軸;6—滑動軸承;7—啟動齒圈;8—飛輪;9—密封圈;10—驅動帶輪;11—正時主動齒輪;12—入口單向閥;13—出口單向閥;14—泵腔;15—柱塞;16—支撐;17—缸間齒輪;18—動力腔圖1 兩缸GCHE結構原理示意圖
曲柄連桿機構位于右側柱塞的右側,與傳統發動機曲柄連桿機構置于活塞下端不同,減少了整機高度。發動機啟動時,外部動力驅動飛輪與曲軸轉動,連桿隨曲軸運動,帶動柱塞上下往復運動,氣缸內工作情況同傳統發動機[2]。連桿受力復雜,一是受到活塞組件交變載荷作用,二是連桿本身擺動及自身慣性力作用[3]。故連桿的優化設計對GCHE樣機研制有著重要意義。
1 GCHE連桿參數優化模型
連桿優化問題可以描述為:將連桿結構尺寸定義為設計變量,將變形、應力等定義為約束函數,將最小體積定義為優化目標[4]。為方便優化,用連桿的1/2模型簡化來代替進行優化,如圖2所示。
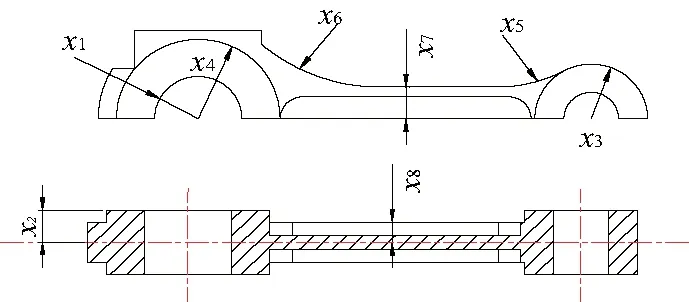
圖2 連桿優化模型
1.1 設計變量
連桿設計變量的尺寸參數選擇應滿足以下要求:對連桿應力、體積、穩定性等影響較大;能反映出連桿的結構外形;對連桿整體結構影響較大,同時不影響其他零部件主要尺寸等。連桿模型中設計變量有8個[5]。初始取值如表1所示。
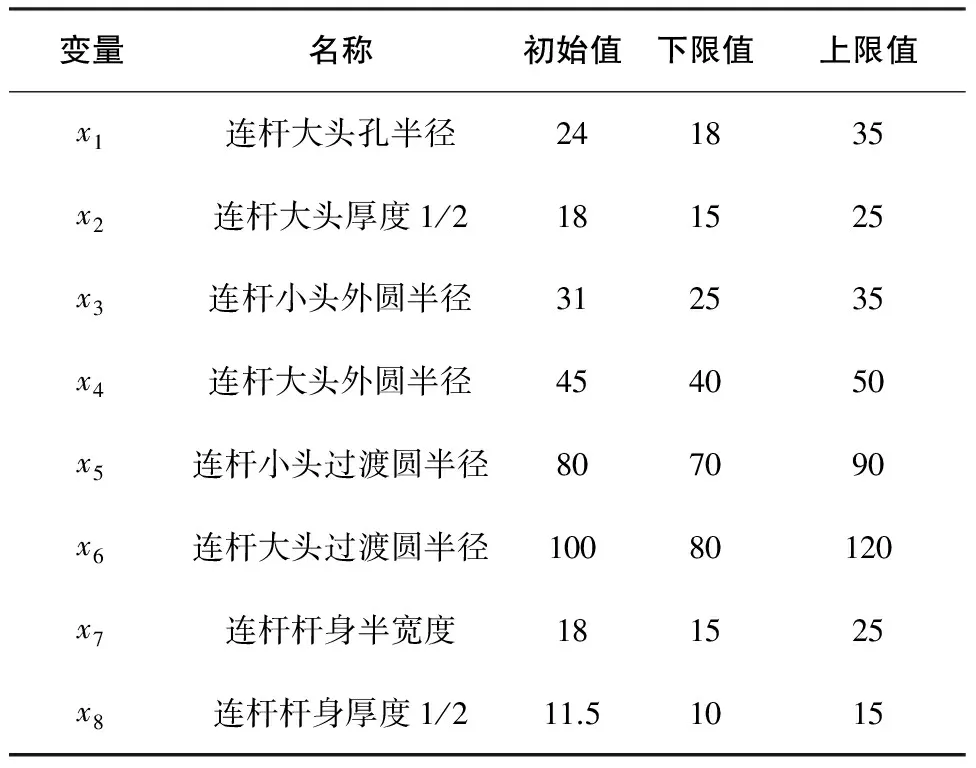
表1 連桿模型設計變量及取值范圍 mm
1.2 約束函數
連桿在運動過程中,由于受力復雜,會發生疲勞斷裂或過量變形等損壞。所以,連桿在滿足輕質的同時,還必須要保證有足夠的強度和抗疲勞性能,同時又要求有一定的剛度和韌性[6]。
1) 疲勞應力約束
σmax≤σ-1/[n1]
(1)
式中:σ-1為連桿疲勞應力極限;[n1]為安全系數。
其中:
(2)
式中:Kσ為油孔邊緣應力集中系數;εσ為結構尺寸影響系數;β為工藝系數;σα為應力幅,單位為MPa;ψα為角系數;σm為平均應力,單位為MPa。將式(2)代入式(1)求得連桿疲動應力。
2) 穩定性約束
σx≤σcr/[n2]
(3)
式中:σx為連桿壓應力;σcr為臨界壓應力;[n2]為穩定性安全因數。
臨界壓應力σcr可由式(4)求得:
(4)
式中:E為彈性模量;I為連桿慣性矩;μ1為連桿長度因數;l為連桿長度;A為橫截面面積。
3) 剛度變形約束
(5)
式中:ΔRmax為連桿大頭的最大變形量;T為配合間隙,取值為0.12mm。由于在分析過程中對連桿小頭外徑末端施加全約束,所以最大剛度水平方向上的變形只考慮連桿大頭部分。
1.3 目標函數
目標函數為連桿體積V(Xr)最小。綜上所述,GCHE連桿的優化模型為:
(7)
式中:△Rmax(Xr)為連桿大頭最大變形,最大值為0.18mm;σmax(Xr)是連桿疲勞應力,最大值為2.78×108Pa;σx(Xr)是連桿穩定應力,最大值為1.865×108Pa,目標函數是使連桿體積V(Xr)最小。
2 近似組合模型分析
組合近似模型(ensemble of metamodel)是由多個近似模型(如多項式、徑向基函數、Kriging和支持向量回歸等)加權線性疊加構成的[7]。公式如式(8):
(8)
式中:yEN為響應預測值,M是單一近似模型的個數;ωi和yi分別為第i個模型的權系數和響應預測值;設計變量x為矢量。此外,式中權系數之和應等于1[8]。
組合近似模型的關鍵是計算權重系數,公式如式(9)-式(11):
(9)
(10)
(11)
式中:Ei為第i個單一近似模型的方均根誤差 (generalized mean square error, GMSE);為所有單一近似模型的平均GMSE;M為近似模型的個數,這里為2。α和β為近似模型控制參數,α和β分別為0.05和-1時,組合近似模型精度較高。
為進一步提升優化的精度,建立如圖3的優化流程。由式(8)-式(11)得到精確權系數值,并由此對組合近似模型輸出連桿優化后的體積,如圖4所示。連桿應變及應力擬合圖如圖5、圖6。組合近似模型得到的響應值基本能和試驗中ANSYS計算出的數值相符合,嚙合程度非常高,可以用此組合模型代替實體模型來進行模擬仿真與優化。
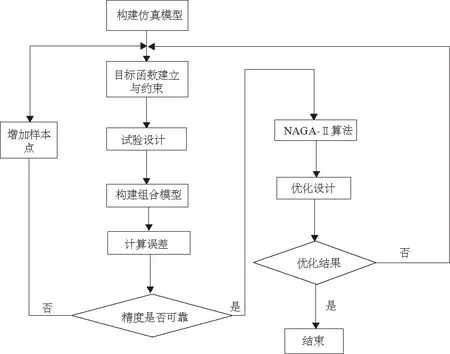
圖3 優化流程圖

圖4 組合優化連桿體積擬合圖

圖5 連桿應變擬合圖

圖6 連桿應力擬合圖
近似模型的精度具有一定限制,采用組合近似模型的方法可以充分考量精度最大化,以使模型精度達到能夠代替實體模型進行優化的目的。如表2,以均方根誤差RMSE和確定性系數R2來檢驗模型的精度,并附以確定性系數R2的箱線圖來比較幾種近似模型的精度差別,如圖7所示。

表2 近似模型精度檢驗
3 模型求解
在Isight軟件中搭建優化平臺,該優化模型由兩個組件構成:Simcode組件與Optimization優化組件,如圖8所示。連桿優化方法選用NSGA-II (Non-dominated sorting genetic algorithm II)算法。
經過73次迭代優化,最終滿足約束條件的最小體積為1.425 0×10-4m3,與初始體積1.929 2 ×10-4m3相比減小了26.13%,優化效果顯著,其體積變化如圖9所示,優化后結果如表3。連桿各設計變量均有明顯的減小,滿足實際工程應用所需。
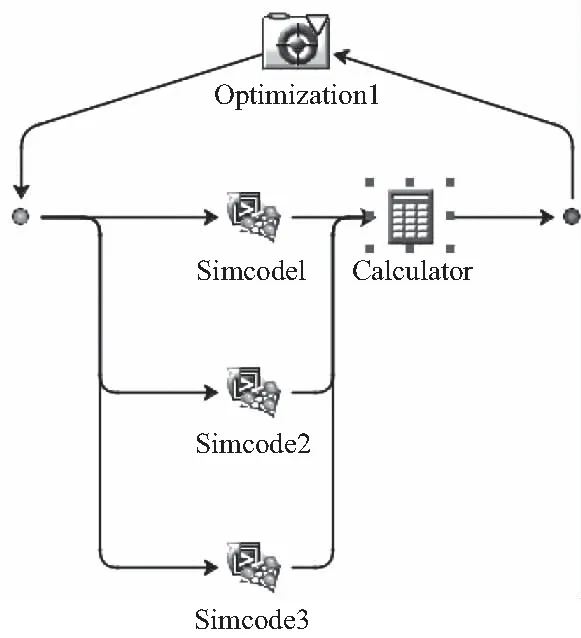
圖8 Isight中連桿優化模型

圖9 連桿體積變化
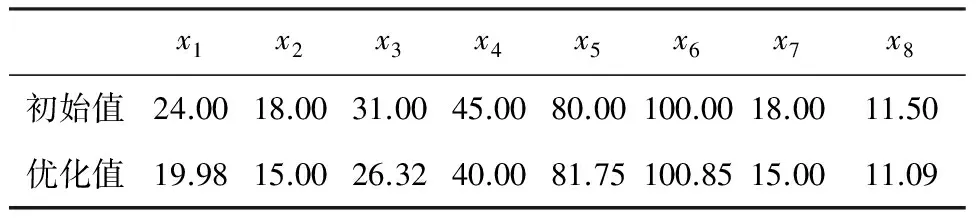
表3 連桿優化結果mm
4 優化結果驗證
經驗證連桿最大疲勞應力為2.647 5×108Pa,穩定應力為1.297×108Pa。拉力下最大變形為1.75×10-4m,如圖10所示,受力云圖如圖11所示。
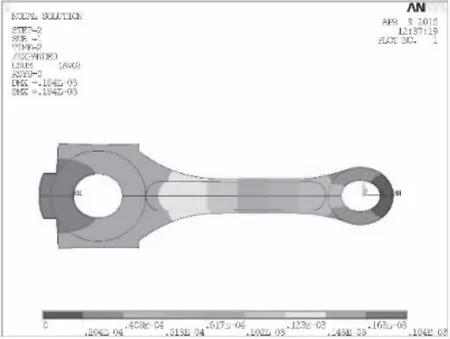
圖10 連桿受拉力時變形云圖
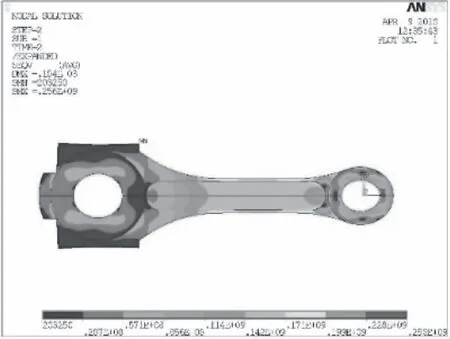
圖11 連桿受拉力時受力云圖
連桿受壓力時最大變形為7.13×10-5m,變形云圖、受力云圖見圖12,圖13。

圖12 連桿受壓力時變形云圖

圖13 連桿受壓力時受力云圖
通過優化結果驗證,得到最優值下各約束條件數值,均符合要求,并分別得到最大拉力、最大壓力兩種工況下變形、受力云圖,該優化結果可應用于連桿設計中。
5 結語
近似模型方法,能夠快速方便地開展各種類型的優化設計研究,包括無約束(有)優化、多目標優化、可靠性優化、穩健優化以及多學科優化設計等。幾種主流近似模型雖各有優勢,在某些特定場合及特殊條件下仍然具有一定的局限性。組合近似模型充分考慮到連桿優化中的問題,較精確地反映出連桿在各種工況下的優化問題,明顯優于單一的近似模型對連桿進行的優化。優化后連桿體積明顯減少,優化效果顯著。基于組合近似模型的GCHE連桿優化,能夠精確得出設計變量對輸出響應的影響程度,可有效減小計算量,在優化中有很好的工程價值。
[1] 張洪信. 一種齒輪聯動液壓發動機: 中國, CN201310015184.4[P]. 2013-04-18.
[2] 舒培, 張洪信, 肖汝琴,等. 缸間齒輪聯動液壓發動機結構設計與研究[J]. 現代制造工程, 2015(5):53-57.
[3] 趙清海, 張洪信, 張鐵柱,等. 液壓約束活塞發動機連桿優化設計[J]. 機械傳動, 2010, 34(1):30-34.
[4] 舒培. 缸間齒輪聯動液壓發動機虛擬樣機技術與動態特性研究[D]. 青島:青島大學,2015.
[5] 高雷. 缸間齒輪聯動液壓發動機曲柄連桿機構協同優化設計[D]. 青島:青島大學,2016.
[6] 孟祥蹤. 基于三缸HCPE虛擬樣機的動力學仿真分析及連桿優化設計[D]. 青島: 青島大學, 2012.
[7] 潘鋒. 組合近似模型方法研究及其在轎車車身輕量化設計的應用[D]. 上海:上海交通大學,2011.
[8] 呂曉江,谷先廣,王國榮,等. 基于組合近似模型的可靠性優化方法在行人柔性腿型碰撞中應用研究[J]. 機械工程學報,2016,52:142-149.

