月球著陸器用磁流變液緩沖器設計與研究

趙鑫光，陳金寶，王宸，魏君

(南京航空航天大學 航天學院，江蘇 南京 210016)

0 引言

磁流變液(MRF)是一種通過在特定的載液(硅油、礦物油等)中添加磁性粒子形成的“智能”懸浮液。無磁場時，磁流變液呈現出流體的狀態；施加磁場時，呈現出半固體的狀態。目前，它已經在工業中得到廣泛應用，包括緩沖器、阻尼器剎車和離合器等[1-3]。

目前，很多國家都對磁流變液進行了研究，其中美國在磁流變液工程化應用方面做出了突出的貢獻。1991年，TRW公司的Shtarkman研制了一種應用到汽車懸架主動控制系統中的旋轉式吸震器；1993后, Lord公司在磁流變液研制方面取得很多重要成果,并已有多款產品面市[4]；Notre Dame 大學的Dyke和Spender等人將其應用到了大型結構的地震響應控制中； Ford公司的 Ginder等人通過有限元分析軟件分析了磁流變液的屈服應力[5]；GM公司的Foister和Gopal Swamy等人研制了幾種磁流變液和磁流變離合器[6-8]；美國加州州立大學的Zhu和Liu 等人對磁流變液微觀結構的流變特性進行了研究；美國匹茲堡大學的Gence和Phule 對不同尺寸粒子的磁流變液的屈服應力進行了研究[9]；Ciocanel等人根據粒子對模型建立了磁流變液的動力學理論，并推導了在不同磁感應強度和剪切速率下的磁流變液的瞬態剪切應力[10]。

除此之外，德國BASFAG 的Kormann 等人研制了穩定的納米級磁流變液；日本的Yamagata 大學對磁流變離合器進行了研究[11]；白俄的Kordonski等人在磁流變液性能以及磁流變拋光、密封等方面的研究取得了重大進展；法國Nice 大學的Bossis 和Cutillas等人對磁流變液的流變機理以及微觀結構進行了大量的研究；韓國Inha 大學對車載可控保險杠磁流變緩沖器進行了研究[12]。

在國內主要是研究所和高校對磁流變液的流變機理、產品開發、控制策略和應用進行了一些研究，并取得了一定的成果。重慶材料研究所研制了一種橋梁拉索抗風振阻尼器，并應用到重慶外環觀音巖大橋上；哈爾濱工業大學的歐進萍、關新春等人研制了不同尺寸和類型的磁流變液阻尼器，并應用到山東濱州黃河大橋和渤海某海洋平臺的振動控制中[13-15]。

通過工業應用，人們在磁流變液的設計和生產制造方面已經積累了大量的經驗，并且其應用到月球著陸器的可行性由李洪波得到驗證[16]。月球著陸器在最終著陸階段會受到強烈的沖擊，緩沖系統在此過程中將發揮重要作用。目前，“軟著陸”是著陸的主要形式，表1是目前被廣泛使用或研究的3種緩沖器，液壓緩沖器、鋁蜂窩緩沖器和磁流變液緩沖器的性能比較。

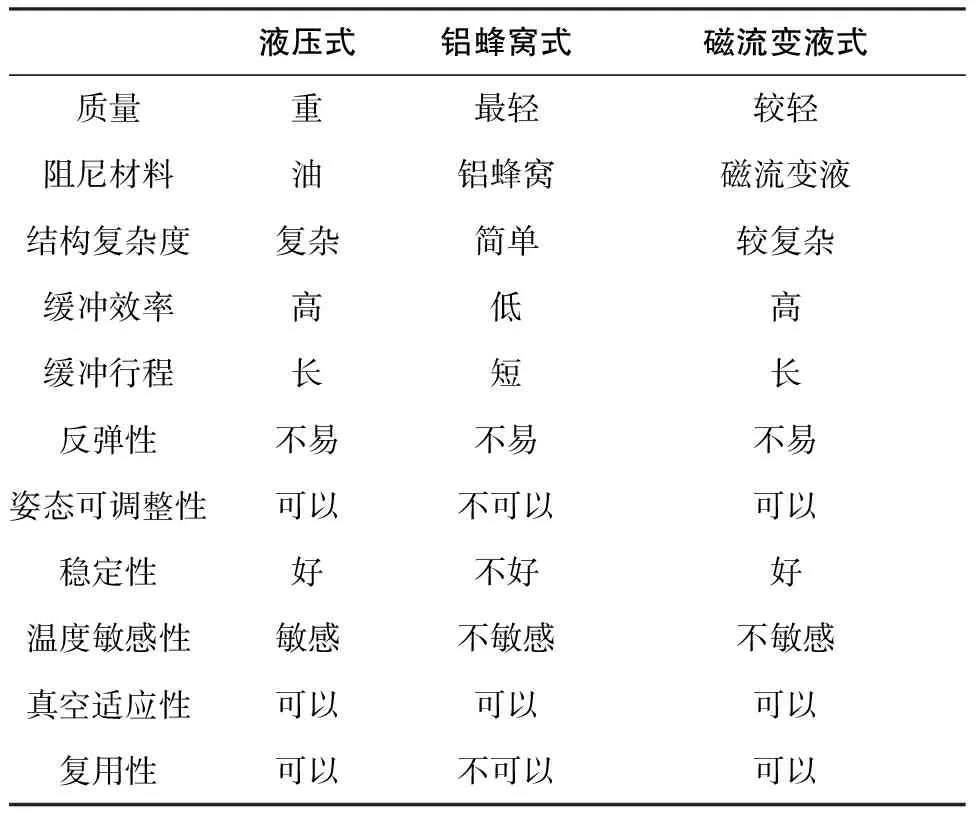
表1 3種緩沖器的性能比較

由表1看出，和鋁蜂窩緩沖器相比，磁流變液緩沖器具有高緩沖效率、長緩沖行程、姿態可調整、良好的穩定性和可重復使用的優勢。并且，和液壓緩沖器相比，它還具有質量較輕和溫度不敏感的優點，這在緩沖器的設計中尤為重要。

通常，軟著陸的時間在0.5s左右，因此對磁流變液緩沖器的控制策略要求很高。由于在線計算時間短，像狀態控制的半主動控制策略被廣泛研究并應用到磁流變液緩沖器的控制中。時間延遲可以被急劇減小，使得將其應用到月球著陸器的緩沖系統中變成可能。同時，隨著我國地外天體探測的深入發展，需要研制出一種可以在復雜著陸環境中使用的著陸緩沖系統。因此，磁流變液緩沖器是設計中一個不錯的選擇。

1 緩沖器選擇

MRFD通常被分成以下4類:

1) 單頭閥式

2) 單頭剪切閥式

3) 雙頭剪切閥式

4) 雙頭旁路剪切閥式

月球著陸器通常會被從一個設定的高度以一定的初始速度釋放，且不能承受大過載，則需要緩沖器具有較大的緩沖行程。和單頭式相比，雙頭式一般具有更大的緩沖行程，其中旁通式的設計，使其更易于進行熱控制，則雙頭旁路剪切閥式緩沖器在應用到月球著陸器中，具有獨特的優勢。

因此，選用雙頭旁路剪切閥式緩沖器作為研究目標，結構簡圖如圖1。L0、L為主缸和旁通缸的長度；D0、D為主缸和旁通缸的直徑；vh為活塞的速度；Lh為活塞的厚度；d為間隙的厚度。

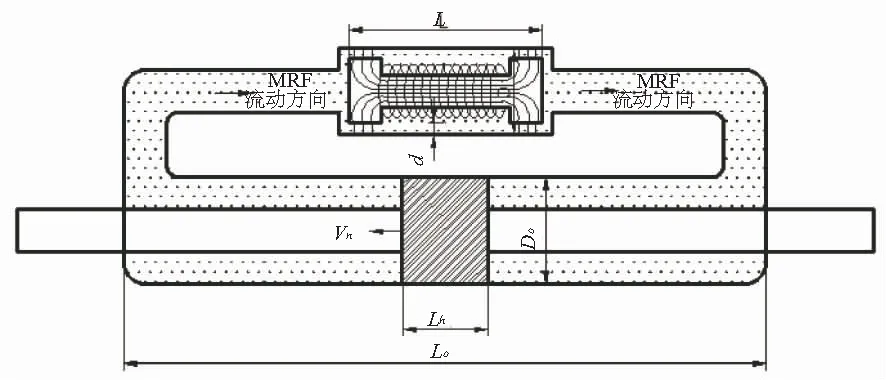
圖1 MRFD的結構簡圖

2 旁通缸阻尼力

Bingham模型并沒有反映出，當磁流變液在高剪切速率下出現剪切稀化的現象，而Herschel-Bulkley模型修正了此模型，考慮了流變過程中的剪切稀化的現象[17]。間隙處的速度分布如圖2所示，其剪切應力τ和剪切應變率dv/dy的關系式是:

(1)

式中：τy(H)是在不同磁場強度下的剪切屈服應力；K是磁流變液的粘度；n是磁流變液的表現系數。

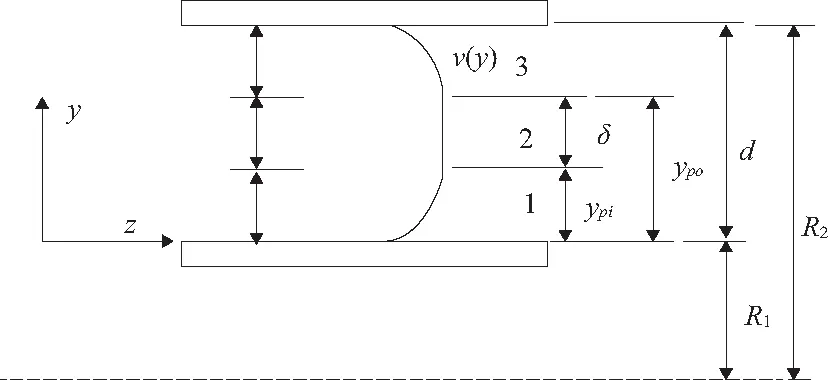
圖2 Herschel-Bulkley模型間隙速度分布圖

圖2中v(y) 是不同y對應的速度；R1和R2分別是內桿直徑和外筒內徑；d,ypi和δ分別是間隙、屈服前區域1和屈服后區域2的厚度。間隙處速度的分布是對稱的，則有：ypi=(d-δ)/2和ypo=(d+δ)/2。

文中，把磁流變液看成是不可壓縮的。則根據Herschel-Bulkley模型，具有以下關系式：

(2)

其中，L是指阻尼區的長度。積分后，可以得到：τ(y)=(ΔP/L)y+C。利用邊界條件：τ(ypi)=τy和τ(ypo)=-τy, 則屈服后區域厚度δ可以得到：δ=2Lτy/ΔP。

聯合式(1)和式(2), 可以得到:

(3)

其中,A1和A2是常數。

對于屈服前區域1、3和屈服后區域2，有以下邊界條件：

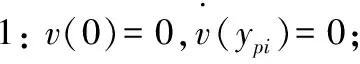
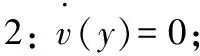
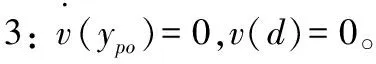
代入式(3)中，各個區域的流速：

(4)

(5)

(6)

則，每個區域的流量：

(7)

(8)

(9)

總流量為:

(10)

即：

(11)

流量和流速具有以下關系：

|Q|=A|v|

(12)

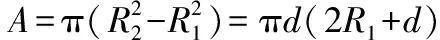
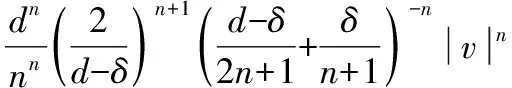
(13)

將δ=2L*τy/ΔP帶入式 (13)中，有：

(14)

當n=1時，式(14)可以簡化為Bingham模型：

ΔP(dΔP-2L*τy)2(dΔP+L*τy)=12KL*dΔP3|v|

(15)

(16)

式中第三項遠小于前兩項的和，則式(16)可以簡化為：

(17)

根據基本的壓力公式：

F=A·ΔP

(18)

對于間隙處，有A≈πd(R1+d)，則有：

(19)

根據流量守恒Av=Ahvh，式(19)也可以寫成以下形式：

(20)

其中，Ah=π(D02-Dr2) /4表示主缸處的橫截面積，vh是活塞的速度。

3 旁通缸參數設計

旁通缸參數包括：長L，直徑D，外筒厚度Δ，間隙厚度d，內桿兩端直徑R，內桿中部直徑D1，內桿中部長度L1，和內桿兩端長度L2，如圖3所示。

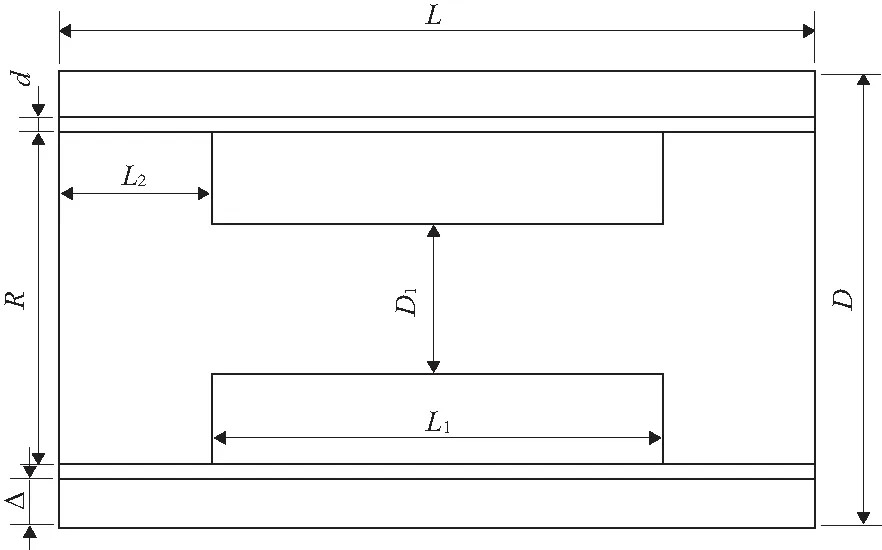
圖3 旁通缸阻尼區結構簡圖

3.1 間隙厚度

內桿和外筒采用高磁導率的材料，并忽略漏磁影響。間隙處的磁場強度遠遠大于其它區域的磁場強度。根據Kirchhoff定律:

NI=∑Hili

(21)

則有：

NI≈2Hd

(22)

說明間隙厚度越小，磁場強度越大。通常，旁通缸的間隙厚度的范圍是0.25～2mm，考慮到加工的難度，取d=1mm。L=2L2，A≈πd(R1+d)，則式(20)可化為：

F=2.688×106×Ah|vh|L2+6π(R1+0.001)×L2τy(H)=L2×(2.4×107×KAh|vh|+6π(R1+0.001)×τy(H))

(23)

由于τy(H)是隨旁通缸的尺寸和外加磁場變化的，而磁場強度是由外加電流決定的。所以，下面的工作就是探究旁通缸的其它尺寸、電流和線圈對阻尼力的影響。

3.2 線圈

本文選用Lord公司的MRF-132DG，采用烴基載液，可以工作在閥模式或剪切模式下，工作溫度是-40 ℃～130 ℃，閃點高于150 ℃，則MRF-132DG可以基本滿足設計的需要。通過改變所加磁場，間接控制MRF-132DG的屈服應力。其特性如圖4所示。

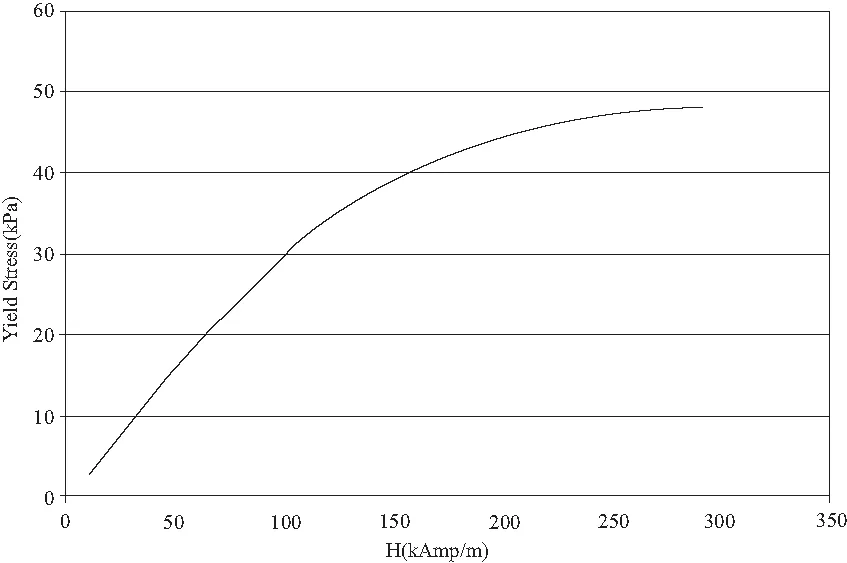
圖 4 屈服應力磁場強度的關系曲線

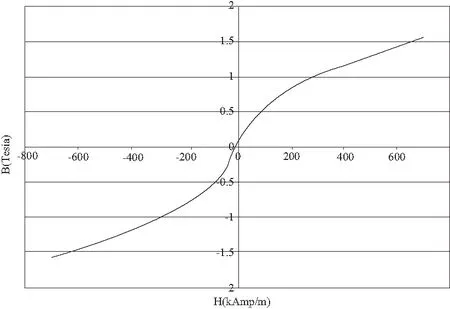
圖5 磁感應強度與磁場強度的關系曲線

對圖4采用5階近似，得到擬合曲線關系式：

(24)

同樣，對圖5的第一象限的曲線擬合得到關系式：

H=288.1×B2+3.654×B+8.277

(25)

對式(23)和式(24)進行數字擬合，得到磁感應強度和屈服應力的關系曲線，如圖6所示。

圖6 屈服應力隨磁感應強度B的變化曲線

通過改變線圈的電流的大小，可以改變阻尼區的磁感應強度，如果知道電流與磁感應強度的關系式，則磁流變液的屈服應力就可以算得。如圖4所示，當磁場強度≥286 kA/m時，屈服應力達到最大。根據公式NI≈2Hd，則設計中的最大NI應≥572A。如果最大電流I已知，則線圈的圈數就可以求得。

3.3 內桿尺寸

由圖7所知，內桿中部的磁感應強度通常遠小于兩端的磁感應強度，則可以忽略中部產生的阻尼力。仿真發現，當NI一定時，內桿中部的尺寸長度對磁感應強度影響不大。因此，內桿中部的尺寸主要取決于使用何種線圈。

為了探究內桿尺寸對阻尼力的影響，經試驗分析，暫令NI=800 A,L1=60 mm,L2=10 mm,Δ=4 mm,D=50 mm,D1=20 mm，通過ANSYS仿真，可以得到不同內桿兩端直徑時，對應的磁感應強度分布圖，圖7是當R=32 mm時的仿真結果。取其平均磁感應強度，通過式(24)和式(25)來求得對應的屈服應力。

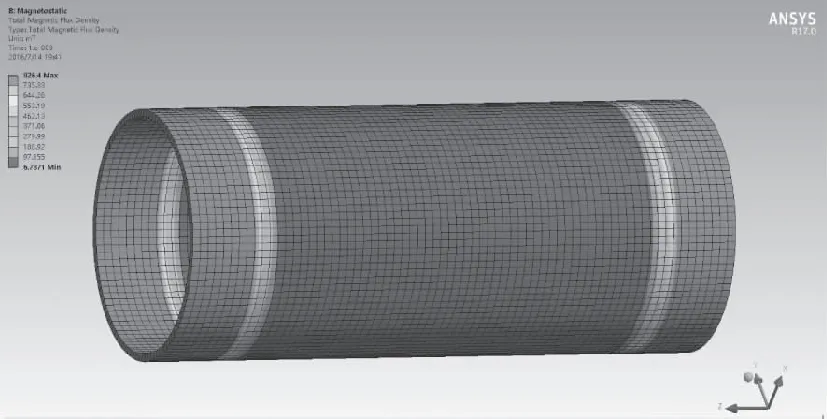
圖7 R=32 mm時，磁感應強度分布的仿真結果

當活塞速度確定時，間隙處的流速會隨內桿兩端直徑的變化而變化，不能達到控制變量的目的，則我們可以采用式(20)求阻尼力。這里令主缸尺寸：D0=100mm,Dr=40mm。將其帶入式中，結果如圖7所示。

由圖8、圖9可知，一定范圍內，磁感應強度和阻尼力都隨R的增大而增大。考慮到R增大帶來的額外質量，取R=44mm。

圖8 R變化對磁感應強度的影響

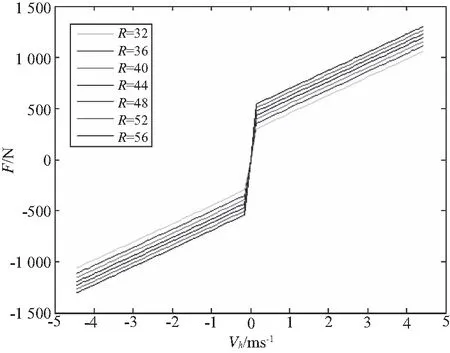
圖9 R變化對阻尼力的影響

3.4 內桿兩端長度L2

為探究L2的變化對磁感應強度的影響，令NI=480 A，以減小電流過大使得磁感應飽和帶來的影響。經試驗分析，取L1=60mm，R=44mm，Δ=4mm，D=50mm和D1=20mm，研究L2的變化對磁感應強度和阻尼力的影響，結果如圖10、圖11所示。

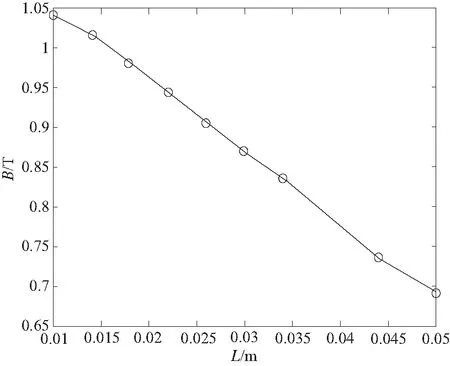
圖10 L2變化對磁感應強度的影響

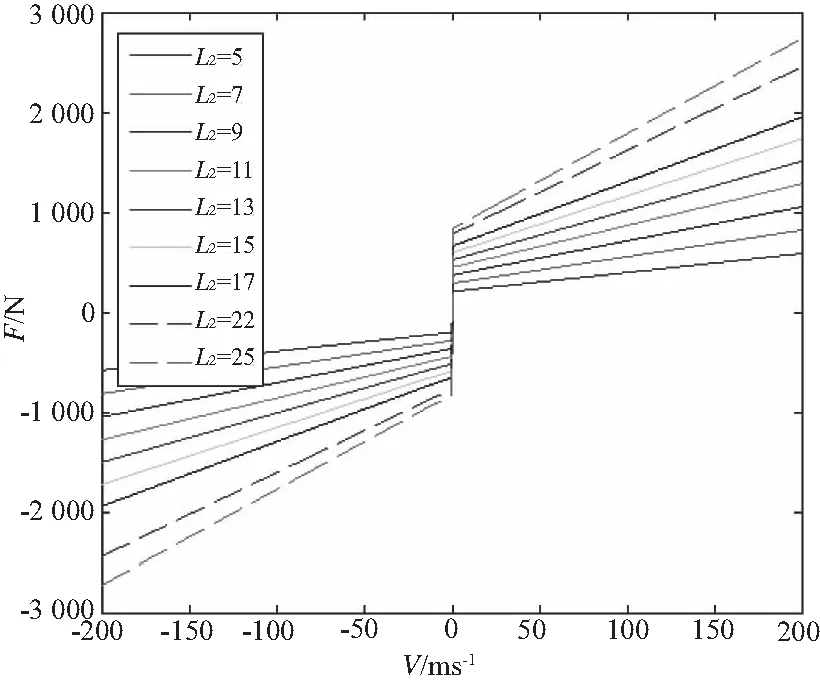
圖11 L2變化對阻尼力的影響

由圖10、圖11可知，在一定范圍內，磁感應強度隨L2的增大而減小，阻尼力隨L2的增大而增大。這里取L2=20mm。

3.5 外筒厚度Δ

令NI=480A，L1=60mm，L2=20mm，D=50mm。根據一般設計準則：Δ/(R+2d)∈(0.08,0.3), 則Δ∈(3.68,13.8)mm。仿真結果如圖12、圖13所示。

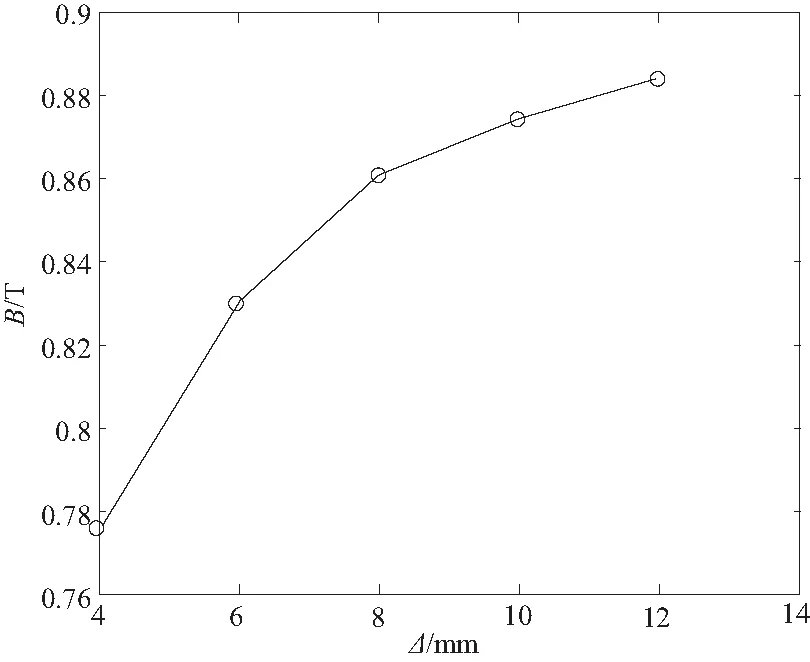
圖12 Δ變化對磁感應強度的影響

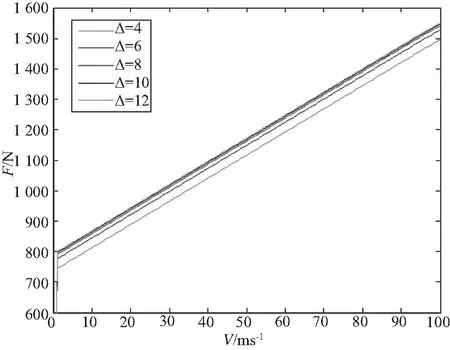
圖13 Δ變化對阻尼力的影響

由圖12、圖13可知，在一定范圍內，隨著Δ的增大，B逐漸變大，并趨于穩定，阻尼力受厚度變化的影響幾乎不大。取Δ=6mm，則緩沖器旁通缸的尺寸如表2所示。

表2 兩種不同硬質合金的物理參數及用途

3.6 電流對阻尼力的影響

根據以上尺寸，建立緩沖器模型。若最大電流Imax=

1A，取N=1 600，則當I=0.5時，NI=800 。研究磁感應強度和阻尼力隨電流大小變化的關系，結果如圖14、圖15所示。

對圖14的磁感應強度和電流的關系曲線采用4階擬合，得到：

B=-0.217 9×I4+1.004×I3-1.889×I2+2.392×I

(26)

聯合式(24)、式(25)和式(26)，屈服應力和電流的關系τy(I)就可以得到。也就是說，可以通過控制電流的變化來改變磁流變液的屈服應力，也就可以間接地控制緩沖器阻尼力的大小。

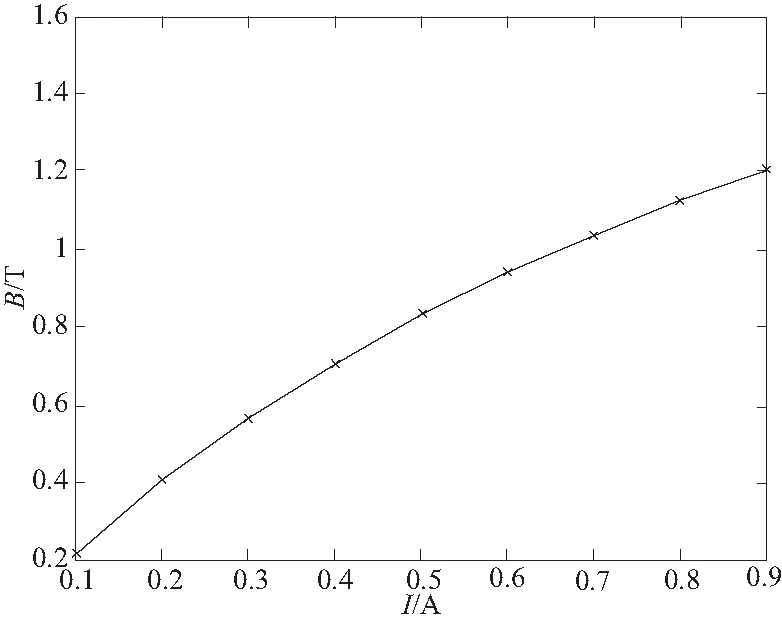
圖14 電流變化對磁感應強度的影響

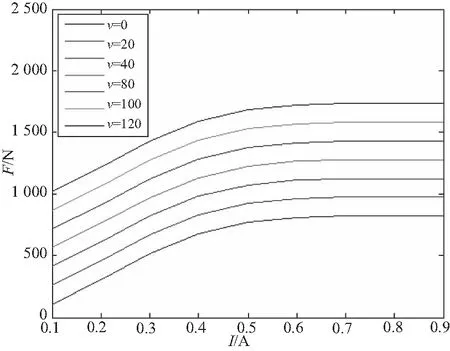
圖15 不同流速下電流變化對阻尼力的影響

4 結語

推導了旁通剪切閥式磁流變液緩沖器的阻尼力算式，并提出了其用于月球著陸器緩沖器中的設計方法。通過仿真分析旁通缸各尺寸對阻尼力的影響，得出以下結論：

1) 當增大旁通缸的各個尺寸時，阻尼力具有持續增大的趨勢。阻尼力的增速正比于內桿兩端直徑R和內桿兩端長度L2的增速，為獲得較大的阻尼力，可適當增大R和L2；

2) 在制造工藝允許的情況下，間隙厚度d越小越好；

3) 旁通缸外筒的厚度Δ對阻尼力的影響不大，則外筒的承受能力是需要首先考慮的要素。

此外，當電流大小一定時，阻尼力會隨流速的增大而增大；當流速一定時，阻尼力會隨電流的增大先增大后逐漸趨于穩定。

近年來，人們已經在磁流變液的研究上取得了許多重要成果，一些實驗顯示磁流變液在溫度-60℃以下時仍表現出一定的流動性。月球上的環境十分惡劣，若要將其完美地應用到月球著陸器的設計中，研究具有良好的高低溫特性的載液將是一個重要的發展方向。

[1] Yang. G. Large-scale magnetorheological fluid damper for vibration mitigation: modeling, testing and control[J]. Dissertation Abstracts International, 2001,6:46-74.

[2] Carlson J.D.Magnetorheological brake with integrated flywheel[P]. US Patent (2001): 6,186,290B1.

[3] Kavlicoglu B M, Gordaninejad F, Evrensel C A, et al. High-torque magnetorheological fluid clutch[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2002, 4697:393-400.

[4] Carlson J.D., Catanzarite D.M., K.A. St. Clair. Commercial magneto-rheological fluid devices [J]. International Journal of Modern Physics B, 2012, 10(10):2857-2865.

[5] Ginder J M. Behavior of Magnetorheological Fluids [J]. Mrs Bulletin, 2013, 23(8):26-29.

[6] Ulicny J C, Mance A M. Evaluation of electroless nickel surface treatment for iron powder used in MR fluids[J] .Materials Science and Engineering, 2004, 369(1/2):309-313.

[7] Foister R T. Magnetorheological fluids [P]. US Patent: 5667715,1997.

[8] Gopal Swamy S. Magneto-rheological transmission clutch [P]. US Patent: 5896965,l999.

[9] Gen? S, Phulé P P. Rheological properties of magnetorheological fluids [J]. Smart Materials & Structures, 2002, 11(1):140-146.

[10] Ciocanel C, Lipscomb G, Naganathan N G. A Constitutive Equation for Magnetorheological Fluid Characterization [J]. Journal of Phase Equilibria & Diffusion, 2008, 29(4):305-311.

[11] Kikuchi T, Oda K, Yamaguchi S, Furusho J. Leg-Robot with MR Clutch to Realize Virtual Spastic Movements[J]. Journal of Intelligent Material Systems and Structures, 2010, 21 (15): 1523-1529.

[12] Woo D, Choi S B, Choi Y T, et al. Frontal Crash Mitigation Using MR Impact Damper for Controllable Bumper [J]. Journal of Intelligent Material Systems and Structures, 2007, 18 (12): 1211-1215.

[13] 禹見達，陳政清，王修勇，等. 磁流變阻尼器與拉索振動控制研究[J]. 功能材料，2006(5)：823-826．

[14] 李國發，韓明佐，單翠云，等. 磁流變力矩傳動裝置的有限元仿真及試驗[J]. 吉林大學學報(工學版)，2013，43(5)：1284-1289．

[15] 唐龍，盧利平，岳恩，等. 磁流變液的研究與應用[J]. 重慶理工大學學報(自然科學版),2013(12):44-48.

[16] 李洪波. 磁流變緩沖阻尼器在月球著陸車軟著陸過程中的理論與應用研究[D]. 西安:西北工業大學, 2002.