無損大量程張力傳感器的有限元分析

馬敏毓，趙敏

(南京航空航天大學 自動化學院，江蘇 南京 210016)

0 引言

重裝空投測試系統是一種廣泛用于軍用及民用的復雜的投放系統，空投時大氣數據、飛機的飛行狀態、載荷質量、投放方式、降落傘類型等各種因素都會對空投系統的性能產生影響。其中，翼傘作為精確重裝空投系統中必不可少的一部分，其傘帶的受力分析對空投動力學的模型建立提供重要參數，也是影響飛機動態響應的主要因素[1]。因此，需要一個用于重裝空投的翼傘傘帶的張力傳感器，進行載荷的實時測量，為進一步空投系統和飛機控制系統的設計提供參考依據。

目前國內外專門針對翼傘傘繩張力測量的傳感器較少，市面上可借鑒的有扁平帶式拉力傳感器，如日本KYOWA共和的LBT-A-20KNSA1和美國精量MEAS的EL20-S458等，其量程范圍基本在2 t左右，而且無法自行拆卸。另外像鋼絲繩張力傳感器及吊鉤秤測力傳感器，如寧波柯力吊鉤秤測力傳感器，其量程可滿足，但是無法實現扁平帶狀結構的非破壞測量。

針對目前市場上的傳感器在重裝空投試驗系統中傘帶張力測量時的不足，設計研制一種特殊結構的大量程張力傳感器，其量程可達25 t，除了能夠滿足重裝空投的量程要求，還能夠實現對扁平傘帶無損的測量，安裝方便，對降落傘開傘操作沒有影響。針對所設計的無損張力傳感器結構，通過ANSYS workbench14.5進行有限元分析。在量程范圍內，對其進行受力形變的模擬，首先給出不同受力狀況下傳感器整體結構的受力分布情況，并確保其滿足25 t量程的強度要求，其次對應變片進行建模仿真，得到傳感器輸入-輸出的理論上的特性表達式。通過傳感器的測量實驗，驗證本文所采用的有限元分析方法有效性及正確性。

1 設計原理

1.1 測量原理

電阻應變式傳感器仍以其較高的測量精度和穩定性的特點在眾多應力應變測量中獲得廣泛使用[2]。在借鑒鋼索張力測量時常采用的旁壓式測量原理的同時，結合扁平帶狀的結構設計，設計了如圖1所示的無損張力傳感器結構。

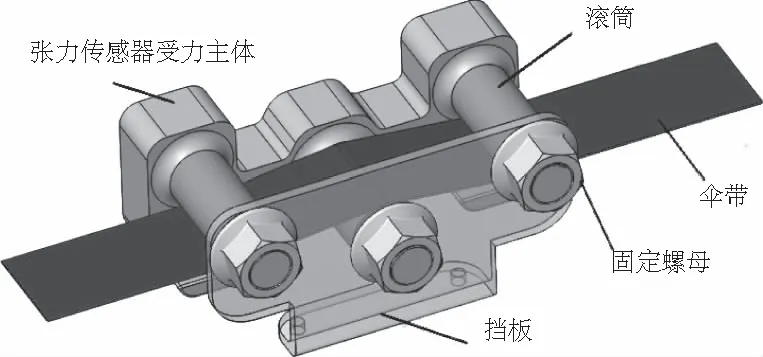
圖1 傳感器整體結構示意圖

傳感器整體由3軸受力主體、滾筒、擋板以及固定螺母組成。其中，受力主體中3個導力圓柱間2個受力梁是承載傘帶張力傳遞的主要彈性結構；滾筒能夠有效地減小摩擦以避免大張力突變情況下傘帶燒蝕現象，實現傘帶的無損測量；擋板及固定螺母起到了對傘帶及傳感器的固定作用。其具體工作過程是：當傘帶受力繃直時會引起傳感器受力主體的變形，從而引起粘貼在受力梁上的電阻式應變片阻值的變化，再通過電橋將應變片的形變轉化為電信號的輸出。

1.2 傳感器受力分布分析

為保證大量程張力傳感器結構的可靠性，一方面需考慮高彈性應變時的超載荷能力，另一方面考慮在低彈性應變時應具有蠕變小、穩定性高等特點，采用的材料最終選擇為42CrMo。該材料屬于超高強度鋼，具有高強度和韌性的特點，常用在負荷較大、可靠性較高的零部件。其力學特性如表1所示。

表1 42CrMO力學特性

在進行有限元分析時，將無損張力傳感器受力主體為主要研究對象，傘帶以Ω型穿行于傳感器3個導力圓柱間，具體見圖2所示。當傘帶兩端受拉力作用時，傘帶繃直對傳感器3個受力軸分別有壓迫作用，從而帶動傳感器彈性結構形變，因此需要建立正確的力學模型進行仿真。本文所設計的無損張力傳感器通過角度轉換[3]的方式，有效減小施加在傳感器上壓迫力，可實現用較輕薄的結構滿足重裝空投25t級張力的測量。

圖2 傘帶傳力模型示意圖

傘帶張力T傳力模型具體可給出的數學關系為：

(1)

可見，α值越小，施加在傳感器上等效力就越小且傘帶接近于拉直狀態，在拉直過程中，傘帶與傳感器接觸面積可視為不變。考慮到張力傳感器3個導力圓柱上套有一定厚度的滾筒，則公式(1)中α值大小采用8° 較為合理。圖3為翼傘傘帶與張力傳感器接觸示意圖，圖中的陰影面積S1、S2、S3為翼傘傘帶和傳感器的接觸面積。根據式(2)可得出具體施加在傳感器上的壓強P，由此就可將傘帶上的張力轉化為對傳感器的壓強加載。

(2)

圖3 傘帶與傳感器接觸示意圖

首先對彈性體進行初步的受力分析，以5t為間隔，分5個載荷步實現力的加載，總量程為25t，受力云圖如圖4所示。應力分布圖顯示出應力較平均的分布在兩側受力梁上，最大的應力即顏色較淺的高亮處，產生在中間的導力圓柱與受力梁的結合處，由表2可知，在25t時最大應力遠小于材料的屈服強度，說明整體結構可滿足強度要求，即測量張力的量程理論上可達到25t。

圖4 彈性體應力云圖

表2 各載荷步最大應力

1.3 應變片的貼片方式及建模分析

張力傳感器的最佳貼片方式的選擇經常采用“應力集中”原則[4]，即在保證應變片所受的應變與彈性體所受的載荷保持嚴格的對應關系的同時，盡可能選擇具有更高應變水平的部位來粘貼應變片，從而提高傳感器的靈敏度。

在張力傳感器實際的應用中，一方面，傘帶在彈性體上的作用點會發生變化，另一方面，彈性體與傘帶間的接觸條件也會發生變化。在這樣的條件下，應變片貼片部位的應力與被測力并不能保證嚴格的對應關系，將造成明顯的測力誤差。為減小這類誤差，在張力傳感器承載強度足夠的條件下，采取在受力臂上打盲孔的方式，具體見圖5 (b)，從而代替傳統的直接將應變片粘貼在梁表面的形式，見圖5 (a)。圖5(c)與圖5(d)表明，盲孔法有效地使應變片貼片位置的應力分布受到盲孔的約束，集中分布在貼片檢測的部位，迫使貼片部分的應變按規律分布，從而減小誤差。另一方面，這種盲孔法貼片還可以將應變片及其接出的引線進行有效保護，避免空投中惡劣的環境對應變片測量準確性產生的影響。

圖5 盲孔法貼片分析

從圖5 (d)中也可看出，盲孔這種突變的結構會引起應力集中，通過這種方法可以將應力引導至合適的位置來粘貼應變片。

張力傳感器上具體的貼片位置如圖6所示，其中位置1處為靠近3個受力軸的所在面，位置2處為背離受力軸的所在面。由于在傳感器標定時采用的應變片是一個矩形片，而不是一個點，為了提高有限元模型求解的準確性，在對應應變片貼片位置處按照應變片的實際大小和形狀單獨劃分網格，如圖7所示。應變片擬采用型號為BE650-4BB(11)的應變片。其特點是“T”型應變計，兩柵互相垂直，見圖7 (a)，主要用于測試軸向應變和橫向應變，也稱為泊松應變，在圖7 (b)中以軸向測量面積來模擬應變片的水平柵測量范圍，以橫向測量面積來模擬垂直柵的測量范圍[5]。

圖6 應變片貼片示意圖

圖7 應變片有限元模型

圖8 擬采用的測量電路

根據四等臂電橋原理，可得：

(3)

其中：

(4)

即：

(5)

有限元仿真分析的加載過程為從0kN開始，以50kN 的差值遞增，直至250kN，共分為5個等級加載，分別測出相應的軸向應變與橫向應變。研究中采用測量面積內所有節點的平均應變作為應變片的測量應變值[7]，仿真數據的匯總見表3所示，其中負值表示應變片所受為壓縮應變。

表3 盲孔中心位置應變片的微應變

由于應變量絕對值的大小最小可以測量到1με的變形量大小，通過表3可看出應變片貼在盲孔中心位置時可以有效反映受力梁形變值，并且在理論上，該傳感器能測量不低于1 000N的張力值[8]。圖9直觀地顯示了張力值與應變值的對應關系呈線性變化，理論上該傳感器的線性度較好。

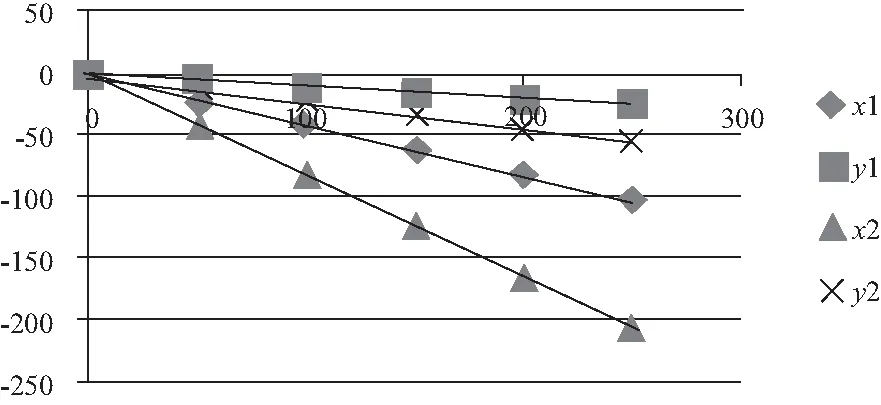
圖9 應變片數據及其擬合曲線

根據擬合直線，可得到盲孔中心位置處載荷與應變之間的對應關系：

(6)

其中，εx1、εy1分別表示位置1處的軸向及橫向應變，εx2、εy2為位置2處的應變，F表示傘帶張力，單位為N。

將式(6)代入式(3)中，并且取靈敏度系數K=2，輸入電壓U=3 300mV，則可獲得傳感器輸出電壓與傘帶張力值之間的關系表達式，即：

Vout=3.3×10-5F-1.04×10-7

(7)

其中，Vout為傳感器實際輸出電壓值，單位mV，F表示傘帶張力，單位為N。

綜上所述，通過有限元法，基于“應力集中”原則，確定采用盲孔法作為應變片貼片方式；通過建立應變片有限元模型，可進一步給出傳感器彈性體加載力與應變值之間的對應關系，從而獲取理論上張力傳感器輸出電壓與傘帶張力間的關系表達式。上述有限元仿真方法可通過與后續實驗數據進行對比驗證。

2 實驗過程及結果分析

2.1 實驗方案

采用實驗結果與仿真結果相對比的方式來驗證上述仿真方法的可行性。具體實驗裝置采用CMT5105的拉力機，該拉力機專用于降落傘強度測試，可提供的標準力最大為100kN。張力傳感器的傘帶可承受250kN拉力。考慮到拉力機本身可提供的最大拉力，將實驗滿量程設定為80kN，可確保拉力機輸出精確的拉力值。

實驗過程中，傘帶以S型穿過張力傳感器，傘帶兩端通過拉力機的夾持裝置將張力傳感器懸吊固定，如圖10所示。拉力機通過對傘帶的拉伸，產生標準力作用于傳感器，后續采用毫伏級電壓表記錄傳感器相對應的輸出電壓值。整個實驗過程，拉力機拉伸傘帶，拉力從零加載至滿量程后，再依次卸載至零，完成一次完整的測量。

圖10 傳感器測量實驗

2.2 實驗分析

實驗的具體加載過程為從0kN開始，以2kN的差值遞增，直至80kN，共分為40個等級加載，分別記錄經放大后的傳感器輸出的電壓值，其中放大倍數設定為105倍。

張力傳感器一次測量實驗數據如圖11所示,其中由于傘帶與傳感器之間仍舊存在的摩擦力，以及拉力試驗機本身在反行程時給出的數據的不確定性導致反行程與正行程存在一定偏差。

經過多次傳感器的測量實驗，采用平移端基直線法對傳感器特性進行分析,并且給出傳感器輸出電壓值與傘帶張力值之間的關系：

Vout=3.475×10-5F+44.375

(8)

其中，電壓輸出Vout單位為mV，傘帶張力F單位為N。并且可得出，未經放大前傳感器輸出電壓值與傘帶張力值之間的關系：

(9)

將式(9)即傳感器輸入-輸出關系式，對比于通過由ANSYS仿真而得的理論數據式(7)，兩者相符合，誤差在可接受范圍內。可見本文所提出的應變片模型及有限元分析方法的正確性，以及其具有的實際指導意義。一方面，可以保證傳感器結構設計的合理性；另一方面，可以從理論上給出傳感器輸入輸出特性的一元線性回歸方程，有效避免復雜結構帶來的復雜數學公式推導。

3 結語

研制一種用于重裝空投中翼傘傘帶的張力傳感器，該傳感器量程大，可達250kN，拆卸及安裝便捷，不會破壞傘帶組織結構。結合有限元方法設計傳感器的彈性體結構，通過有限元法給出的應變分布特性，確定通過盲孔法實現應變片的粘貼，該技術一方面有效地保護應變片及其導線，另一方面能夠顯著提高應力水平，提高測量靈敏度。另外，將應變片結構及貼片位置以軸向與橫向測量面積構建有限元分析測量模型，通過對比ANSYS workbench理論分析出的結果與傳感器實際實驗結果，表明該模型可以正確反映應變片變形，給出正確的理論依據，可以為將來傳感器的進一步研究提供參考。

[1] 黑文靜,林皓. 重裝空投出艙過程對飛機動態響應的影響[J]. 系統仿真學報, 2008(S2):345-347.

[3] 翟慶光,聶杰, 康岳偉. 深海取樣絞車牽引卷筒上鋼纜張力分析[J]. 海洋技術, 2008(2): 28-30.

[4] 孔揚. 對電阻應變片式測力傳感器“應力集中”的探討[J]. 新校園(上旬), 2015(11): 62-65.

[5] 胡玉梅. 應變片敏感柵結構參數對測量精度的影響[J]. 重慶大學學報, 2013(12): 21-27.

[6] 呂泉. 電橋電路對應變片電測法的影響[J]. 鞍山師范學院學報, 2004, 6(4):23-24.

[7] 楊君琦. 應變傳感器的應變傳遞理論及傳感特性研究[D]. 長沙：中南大學,2013.

[8] 楊奕. 微型電子秤用傳感器的研制[J]. 常州工學院學報, 2006(4):9-12，42.