一種新型多自由度混聯運動平臺的設計與仿真分析

羅磊，王培俊，黃琳秦

(西南交通大學 機械工程學院，四川 成都 610031)

0 引言

多自由度運動平臺在模擬駕駛、工業機器人、數控機床等領域應用廣泛，實用性較高[1]。串聯機構工作空間大、結構簡單，但累積誤差大、剛度低；并聯機構剛度大、精度高，但控制難度大、成本高[2]。本文結合串并聯機構的優缺點與實際使用需求情況，設計了一種新型混聯運動平臺，具有4個自由度，以實現剛度大、響應快和應用范圍廣的目標。

新型混聯運動平臺的結構主要由兩部分組成：串聯部分和并聯部分，設計的主視圖如圖1所示。串聯部分由具有回轉機構的轉臺組成，實現動平臺繞Z軸的轉動；并聯部分由3-RPS并聯機構組成，實現動平臺繞X軸、繞Y軸轉動和沿著Z軸的移動，并聯部分的結構簡圖如圖2所示。

根據運動平臺的串聯部分的特點，計算運動平臺在串聯部分的姿態變換矩陣；運用歐拉法計算出并聯部分的姿態變換矩陣，從而計算混聯運動平臺末端執行器的坐標系坐標；運用空間幾何法，建立末端執行器位置與電動缸總長度關系。在MATLAB中，根據機構的逆解，求解運動平臺末端執行器所能夠達到的最大空間位置，將其與3-RPS并聯機構的工作空間進行對比；在ADAMS中，建立該機構的簡易模型，然后進行各個自由度的動力學分析；采集ADAMS動力學分析的多項數據，在MATLAB中進行誤差分析。

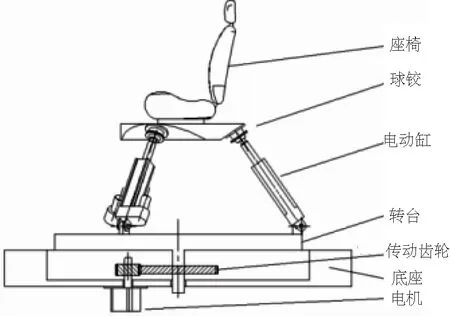
圖1 混聯運動平臺的主視圖

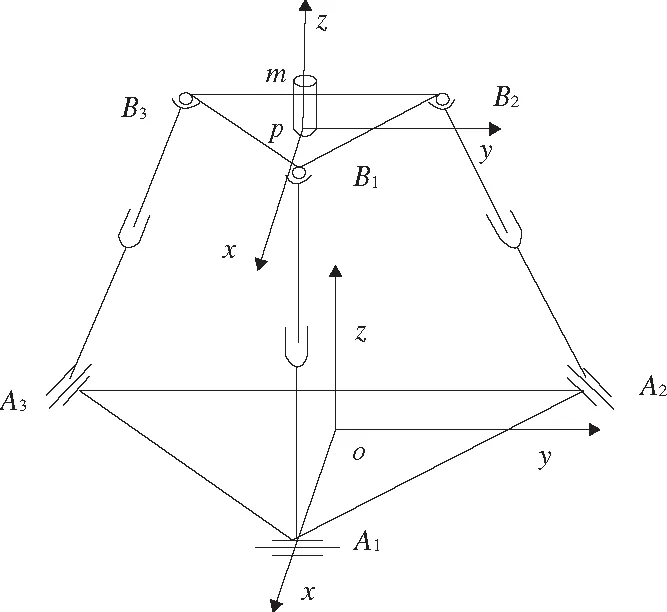
圖2 并聯部分結構簡圖

1 運動學分析

1.1 平臺描述

由于運動平臺的工作環境較為惡劣，需要較大的剛度，運動平臺的工作空間影響著平臺的動力學性能，也決定著運動平臺的使用范圍。運動平臺末端執行器的精度越高，平臺的控制就越精細，累計誤差越小。綜合以上需求，研究設計了一種新型混聯運動平臺，具有結構新穎性和功能新穎性。

結構的新穎性：轉臺的回轉機構由回轉支撐機構和回轉驅動裝置組成。運動平臺工作環境惡劣，對支撐結構的沖擊較大，所以支撐機構的強度必須滿足需求。滾子夾套式機構具有重心低、穩定性高、制造和安裝簡單等優點[3]。設計的回轉支撐機構采用滾子夾套式機構。齒輪機構具有效率高、傳動比穩定和結構緊湊的特點，所以采用齒輪傳動機構作為回轉驅動裝置。在回轉機構的基礎上，在轉臺上安裝3-RPS機構，為整個平臺提供更多的自由度且結構緊湊。

功能的新穎性：相比3-RPS機構，增加回轉機構后，新型混聯運動平臺末端執行器能夠執行更復雜的空間曲線、能夠更真實的反應運動情況。根據運用場合的不同，在轉臺上安裝不同的設備，可構成不同的運動平臺，如汽車駕駛仿真平臺。回轉機構實現平臺的自轉，如實現汽車駕駛仿真平臺的甩尾運動；并聯機構實現平臺的z向移動和繞x、y軸的轉動，如實現汽車駕駛仿真平臺的豎直運動、俯仰運動和側翻運動[4]。

1.2 位置反解

新型混聯運動平臺的運動學逆解求解分兩步，首先求解串聯部分的姿態變換矩陣，再求解并聯部分的姿態變換矩陣。

末端執行器的空間位置可以分解為：o-x0y0z0到o-x1y1z1的旋轉變換、o-x1y1z1到p-x2y2z2的旋轉變換和平移變換[5-7]。整個變換過程，坐標系的位置變化如圖3所示。坐標系o-x0y0z0到o-x1y1z1的姿態變換矩陣為T01，如式(1)所示。

(1)

圖3 運動平臺的坐標變換

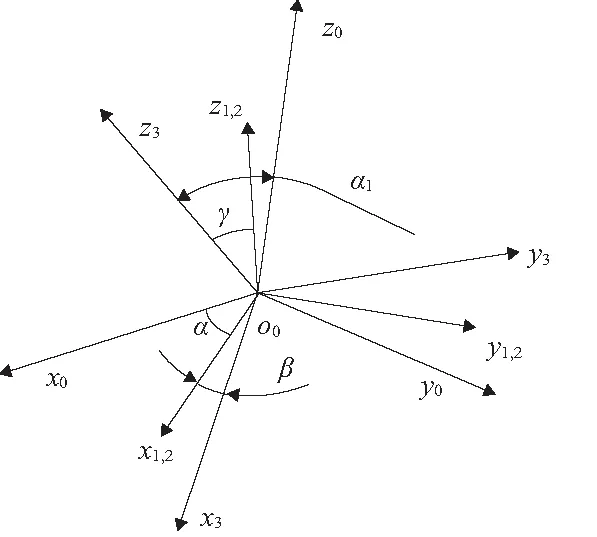
圖4 歐拉角z-y-x坐標系變化

r和R分別為并聯部分的上下平臺的外接圓半徑。根據圖2中鉸鏈和球鉸與對應坐標系的關系，解出A1、A2、A3在o-xyz中的坐標Ai和B1、B2、B3在p-xyz中的坐標bi分別如下：

o-x1y1z1到p-x2y2z2的旋轉變換可用z-y-x歐拉角(α,β,γ)表示，如圖4所示。用z-y-x歐拉角表示的姿態變換矩陣為T12，如式(2)所示。

(2)

其中：sα=sinα，cβ=cosβ,以此類推。

根據歐拉角姿態變換矩陣即可求得Bi的世界坐標系坐標：

(3)

電動缸與轉臺之間以鉸鏈連接。由于鉸鏈結構特性，電動缸只能繞著定軸轉動，那么電動缸所掃過的空間為一個扇形平面。同理，3個球鉸只在3個固定扇形平面內運動，3個平面方程如式(4)所示。

(4)

根據式(2)-式(4)，解得并聯部分的位姿約束方程，如式(5)所示。

(5)

由式(5)可以看出：進動角α是自轉角β和章動角γ的函數，也證明了并聯部分只有2個轉動自由度。

根據式(1)和式(2)，計算出整個運動平臺的姿態變換矩陣為T02，如式(6)所示。

(6)

其中：

為校驗所得到的T02正確性，將平臺的初始位置：θ=0,α=0,β=0,γ=0,xp=0,yp=0,zp=H,帶入矩陣T02計算，計算結果為：

與新型混聯運動平臺的初始位置完全一致，計算結果正確。

在實際使用中，針對不同用途，可以在動平臺上方安裝不同的設備，如汽車駕駛仿真平臺，這將導致動平臺的質心不在動平臺下表面中心處。假設：動平臺的質心在動平臺以上的M點處，將M點設為動平臺參考點。那么，M點的世界坐標系坐標的表示方法，如式(7)所示。

(7)

其中，m為參考點M在p-xyz中的坐標。

1.3 位置正解

根據電動缸的總長度Li、各電動缸軸線與轉臺的夾角φi和轉臺自轉的角度θ，采用立體幾何法，可解出動平臺參考點的世界坐標系坐標。根據已知條件，求解出動平臺B1、B2和B3的世界坐標系坐標，如式(8)所示。

(8)

則，上平臺中心點P的坐標如式(9)所示。

P=B1+B2+B3

(9)

上平臺所在平面的法向量：

(10)

點M位于通過P且與動平臺垂直的空間直線上，直線方程如式(11)所示。

(11)

|PM|=h，即可求出動平臺參考點M繞z軸旋轉之前的世界坐標系坐標。轉臺轉動的角度θ，將其帶入式(1)，解得末端執行器參考點在世界坐標系的坐標如式(12)所示。

(12)

2 工作空間

工作空間是指末端執行器所能夠達到的空間目標的集 合[8]。研究工作空間有利于避免末端執行器與其他部件發生干涉，還能夠為平臺的控制提供數據基礎。

混聯運動平臺的幾個重要設計參數：R=500mm,r=300mm,Lmin=654mm,Lmax=1 152mm,h=300mm。采用數值搜索法，在MATLAB中編寫相應的程序，計算出動平臺參考點M的工作空間，如圖5所示。將其與3-RPS機構的工作空間進行對比。當y=0時，將兩種機構工作空間的xz截面對比，如圖6所示。

圖5 混聯機構的工作空間

圖6 兩種機構的xz截面對比

在MATLAB中，混聯機構的工作空間呈現兩頭尖的錐形分布。根據工作空間截面對比圖，表明混聯運動平臺的工作空間比單一的并聯機構的工作空間大，混聯運動平臺的工作空間在各個方向上都達到了3-RPS的徑向極限位置。

3 動力學分析

在ADAMS中，使用“一般點驅動”和“樣條函數驅動”功能，實現運動平臺的運動。并聯部分的移動副采用樣條函數驅動，串聯部分的轉動副采用STEP函數驅動。

在ADAMS動力學仿真中，整個過程持續10s，分作300步。每個電動缸的鉸鏈中心到球鉸中心的距離為電動缸總長Li，Li的變化曲線如圖7所示。

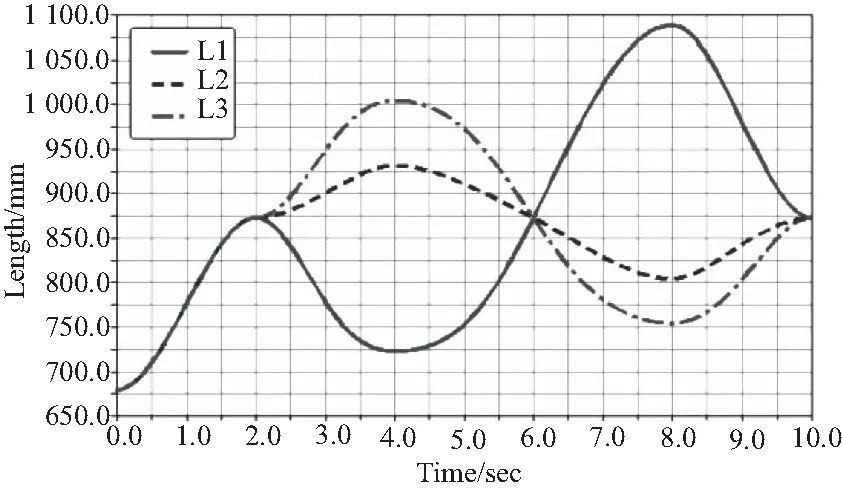
圖7 3個電動缸總長變化

根據ADAMS后處理，獲得電動缸總長、自轉角、球鉸和鉸鏈的夾角變化。利用1.3節中的位置正解方法，在MATLAB中編寫位置正解程序，計算新型混聯運動平臺的參考點坐標。將計算值與仿真值進行比較，得出參考點誤差分析圖，如圖8所示。

圖8 參考點誤差分析圖

由圖8可以看出，xyz向誤差呈現一定的波動。當3個電動缸總長度在接近相等時，參考點的誤差較大，且z向的誤差最小。在xyz方向上，參考點的誤差在4×10-5mm以內，誤差均在允許的范圍內，精度較高，表明運動學方程準確無誤。

4 結語

在MATLAB中，根據位置反解算法，分別對3-RPS機構和新型混聯運動平臺末端執行器的工作空間進行求解。3-RPS的工作空間關于3個鉸鏈約束平面對稱，混聯機構的工作空間關于中心軸對稱。當新型混聯運動平臺的并聯部分與3-RPS機構完全相同時，3-RPS機構的工作空間體積為：V3-RPS=8.313 3×106mm3，運動平臺的工作空間體積為：V混聯=11.687×106mm3，運動平臺的工作空間增加了40.58%。可見，當增加回轉機構后，新型混聯運動平臺末端執行器的工作空間大大增加，體現串聯部分的優勢。

分析新型混聯運動平臺的ADAMS動力學仿真數據，結果表明電動缸的長度、鉸鏈夾角和球鉸夾角變化都在設定的范圍內，末端執行器參考點的空間位置均在工作空間內，表明工作空間求解準確。通過誤差分析，表明新型混聯運動平臺參考點的精度較高，體現并聯部分的優勢。通過動力學分析，為混聯運動平臺的優化和控制提供了動力學依據。

[1] 潘璇，王培俊，聶良兵,等. 基于ADAMS的三自由度汽車運動平臺仿真分析[J]. 機械傳動,2013,37(4):98-100.

[2] 鄭東志,鄭子龍. 六自由度并聯機器人的位置分析及仿真研究[J]. 機械制造與自動化,2016,45(2):163-166.

[3] 高順德,沈云海,苗明. 滾子夾套式回轉支撐輪壓均衡方法研究[J]. 起重運輸機械,2011 (8):81-85.

[4] 張驍,王培俊,張利斌,等. 四自由度混聯運動平臺的分析與仿真[J]. 機械設計與制造,2015(10):241-248.

[5] 鄭魁敬,崔培,郭海軍. 3-RPS并聯機構運動與靜力特性分析[J]. 機械設計,2011,28(9):28-33.

[6] 朱大昌,嚴智敏,崔祥府,等. 基于螺旋理論對3-RPS并聯機器人運動學分析及仿真[J]. 機械科學與技術,2015,32(1):28-31.

[7] K.M.Lee and D.K.Shah. Kinematic Analysis of a Three-Degree-of-Freedom In-parallel Actuated Manipulators[J]. Proc. IEEE Int.Conf. Robotics and Automation,1987(1):345-350.

[8] 王瑞,劉文濤,紀孝娟. 一種新型串并聯機床的工作空間分析[J]. 機械設計,2009,26(5):61-64.