一種面向直接迭代誤差的NLMS-OCF算法研究*
李 茹,翟書穎,李 波
(西北工業大學明德學院,西安710024)
1 引言
歸一化最小均方(NLMS)算法由于其低運算量和易于實現而成為最流行的自適應算法之一。而且此算法針對有限字長的效果是健壯的。但高度相關的輸入信號在一定程度上降低了它的收斂速度[1-3]。在過去幾十年里,有一類等效算法如仿射投影算法(APA)、部分排名算法(PRA)、廣義最佳塊算法(GOBA)、帶有正交校正因子的NLMS算法(NLMSOCF)等已經被用來處理這一問題[4-5]。這些算法的明顯特征就是它們更新權重基于多樣的、延遲的輸入信號向量;而NLMS算法更新權重則是基于一個單一的輸入向量。這整個算法類別可被稱為仿射投影算法,是因為APA在這些算法中是最早出現的,并且APA這個名字比其它的名字更廣泛地使用在現有文獻中[6-7]。當延遲D設置為1時,按文獻[8]中的解釋,APA算法就是NLMS-OCF算法的一個特例。
然而,對于NLMS-OCF算法來說,迭代方向,也稱為自適應權重更新方向,是方向向量;而自適應濾波器的迭代誤差是由輸入向量和自適應濾波器的估計參數引起的。這兩個方向是不一致的,從而對于迭代誤差導致了更多的偏差。在本研究中,嘗試用NLMS-OCF-IE算法解決這一問題。此算法是在無測量噪聲的條件下首次提出;迭代誤差是直接由方向向量引起,方向向量也是自適應濾波器的迭代方向。相應的仿真實驗結果將驗證推導的準確性。
2 NLMS-OCF算法
圖1顯示了一個用在系統辨識模型中的自適應濾波器。如圖,系統的輸入xn和相應的測量輸出dn很可能產生于測量噪聲εn污染之后,是已知的。測量噪聲εn是零均值復雜白噪聲。目標是估計一個N維的權重向量這樣當xn=(xn,xn-1,...,xn-N+1)T是在第n個時刻輸入的向量時,估計輸出在均方誤差意義上,盡可能地接近測量輸出dn。
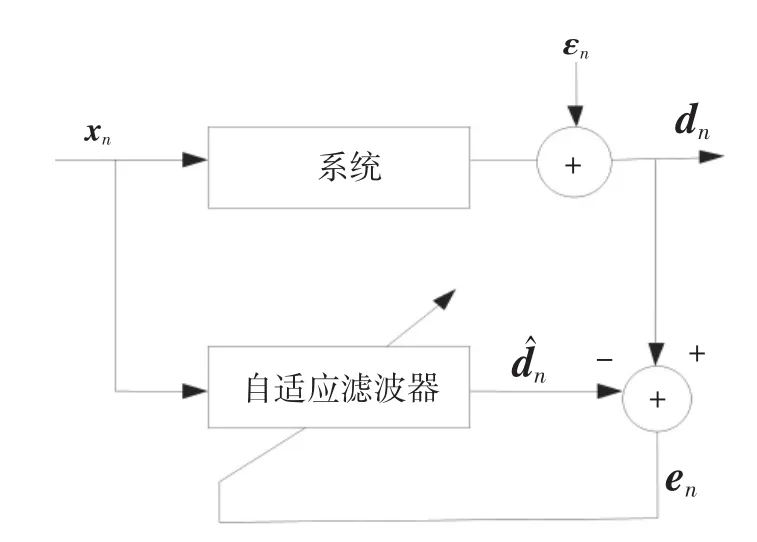
圖1 自適應濾波器的辨識模型
在[8]中NLMS-OCF算法總結如下:任意選取一個正交校正因子的數量對于每一個n重復下面的步驟:
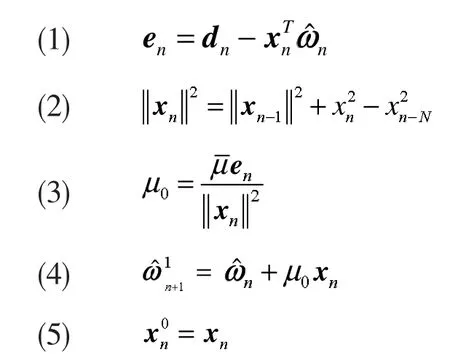
對于 k=1,2,...M,重復步驟(6)~(9)

對于NLMS-OCF算法,從步驟(7)和(9)中可以看出,NLMS-OCF算法權值向量更新的方向是彼此相互正交的,而當D=1時,輸入向量xn,xn-D,...,xn-MD幾乎是平行的,從而延緩了自適應濾波器的收斂速度。權值向量更新的方向分別是向量xn,但是估計誤差分別是由輸入向量xn,xn-D,...,xn-MD引起的,除了向量xn,權值向量更新方向和引起估計誤差的方向是不一致的,即為了解決這個問題,NLMS-OCF-IE算法需要被提出。
3 NLMS-OCF-IE算法
通過分析在權值向量更新方向上的估計誤差,建立了一種NLMS-OCF-IE算法,其估計誤差重新定義為:
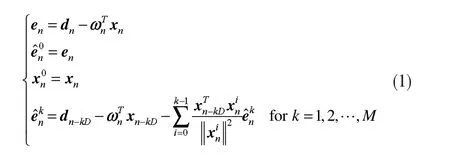
權值向量更新方程式為:
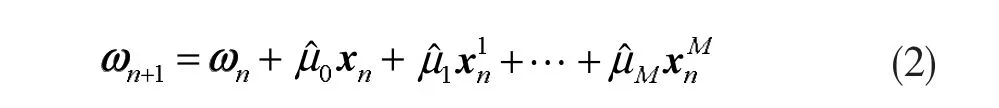
其中
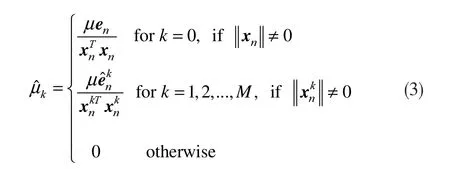
和
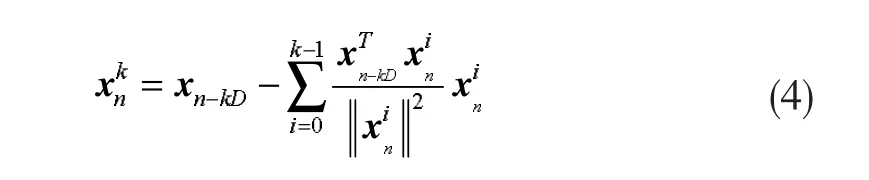
由此,式(1)、(2)、(3)和(4)組成了 NLMS-OCF-IE算法。在下面分析中將證明,在無系統測量噪聲的條件下,估計誤差僅僅是由向量引起的。
假設存在一個真實的自適應濾波器的N維的權值向量ω0,那么理想的輸出應該滿足以下表達式
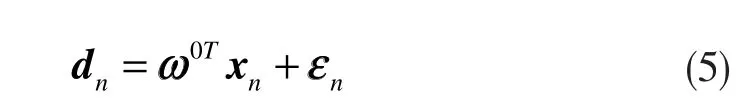
系統測量噪聲是均值等于0、方差是的白噪聲,其獨立于輸入向量xn,那么相應的估計誤差為
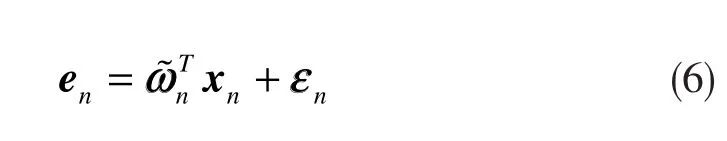
其中

從式(6)中可以知道,在無系統測量噪聲的條件下,估計誤差en僅僅是由輸入向量xn引起的,也就是說它和自適應濾波器的權值向量更新方向是相同的。
從式(1)、(4)、(5)和(6)中,我們可以得到以下的表達形式
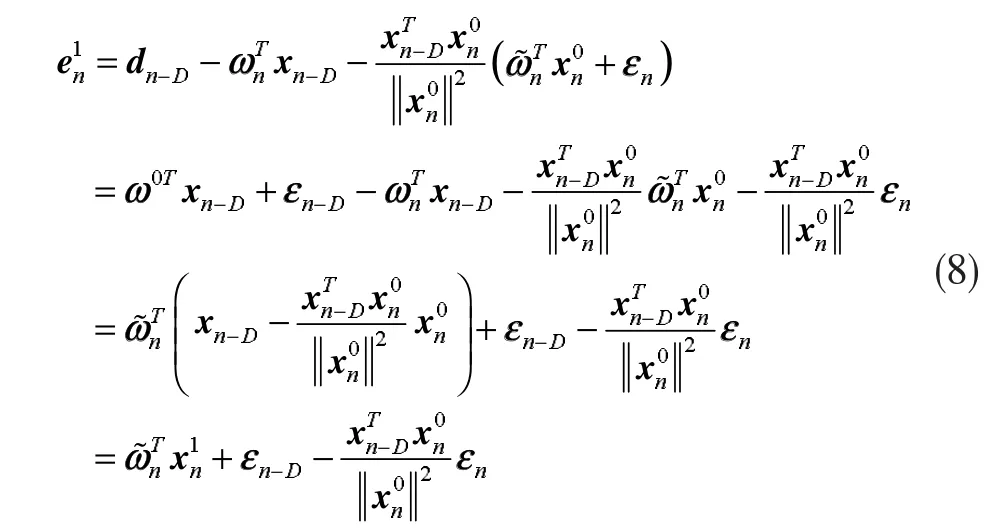
和
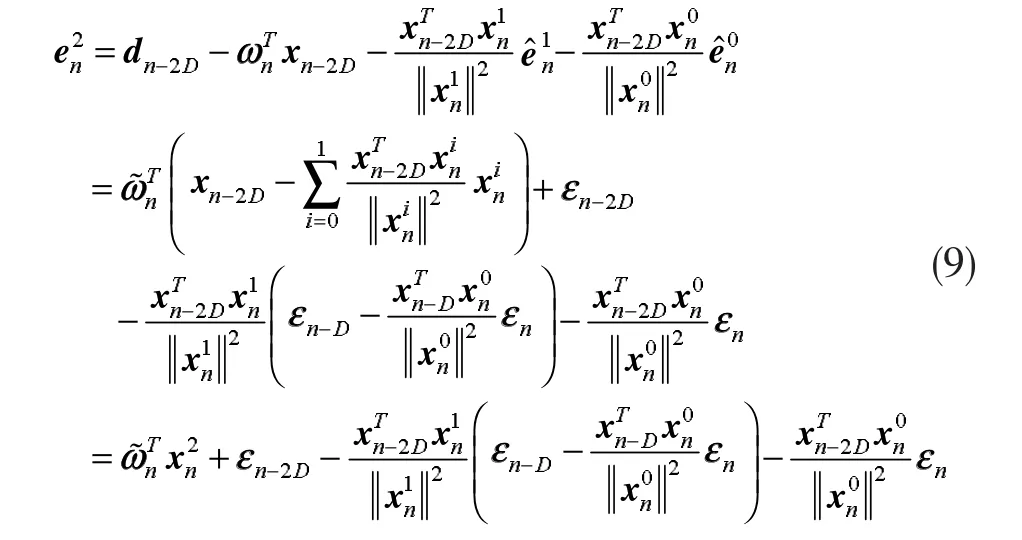
從式(8)和式(9)中可以看出,在無系統測量噪聲的條件下,估計誤差僅僅是由向量引起的,估計誤差僅僅是由向量引起的。下面可以定義:
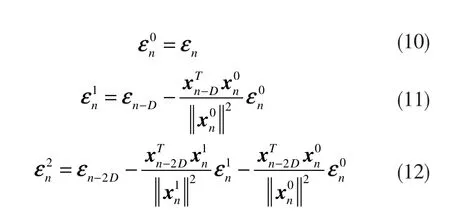
以此類推,可以得到以下表達式
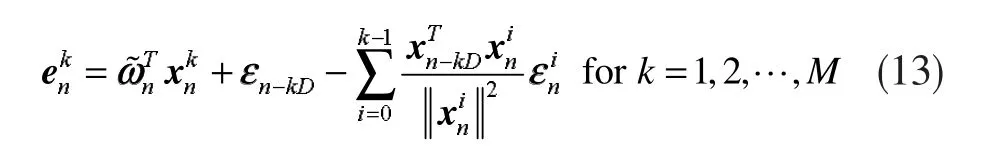
其中
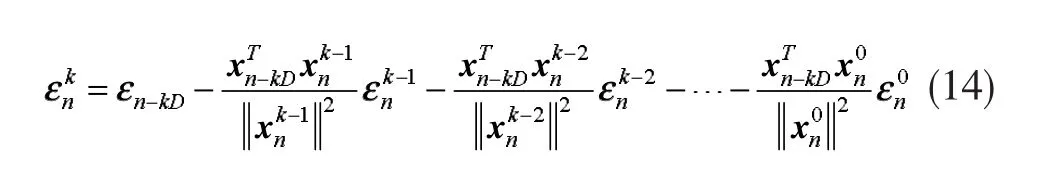
因此,從式(2)、式(3)和式(13)中,可以得出結論:在無測量噪聲的條件下,估計誤差僅僅是由向量引起的,也就是說當k=0,1,...,M時,它也是NLMSOCF-IE算法的權值向量更新方向。
4 仿真示例
以下分別就NLMS-OCF算法和NLMS-OCF-IE算法在MATLAB中進行了仿真,并對兩者的仿真結果做了分析比較。分析包括不同的迭代步長對算法收斂速度產生的影響。仿真結果的MSE學習曲線是通過對100個相互獨立的學習曲線求平均值而得到的。參數迭代步長分別選取為0.1和0.5,參數正交校正因子M=3,維數N=32,測量噪聲是方差等于0-4的高斯白噪聲。當延遲因子D=1時,NLMS-OCF算法與APA算法的特征完全相同,可見APA算法是NLMS-OCF算法的一個特例。因此本文中設置D=1。仿真示例如下。
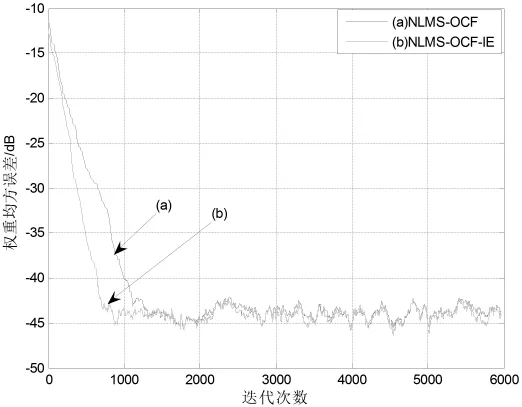
圖2 示例1中迭代步長為0.1時的均方誤差學習曲線
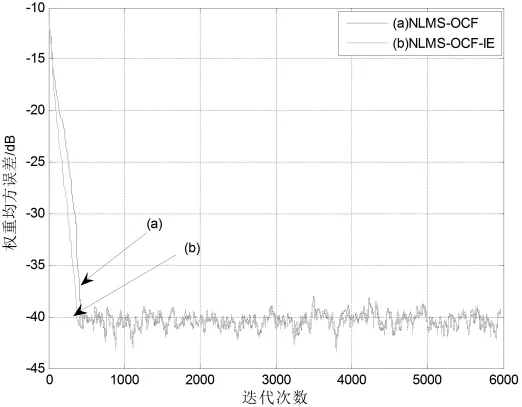
圖3 示例1中迭代步長為0.5時的均方誤差學習曲線
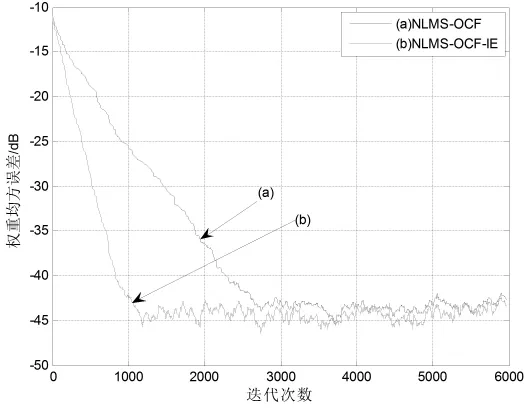
圖4 示例2中迭代步長為0.1時的均方誤差學習曲線
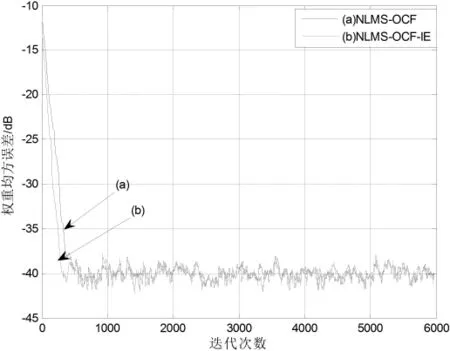
圖5 示例2中迭代步長為0.5時的均方誤差學習曲線
示例1:
考慮表達式為xn=-0.5xn-1-0.3xn-2-0.2xn-3+zn的適度相關的輸入信號模型,其中zn為均值等于0的高斯白噪聲。在此種條件下,對于兩種不同的迭代步長值,NLMS-OCF算法和NLMS-OCF-IE算法的權值向量均方誤差學習曲線如圖2、圖3(見前頁)所示,從對它們的比較中可以看出,NLMS-OCF-IE算法相比于傳統的NLMS-OCF算法得到了比較快的收斂速度,當迭代步長為0.1時效果尤為明顯。
示例2:
考慮表達式為xn=-0.95xn-1-0.6xn-2-0.4xn-3+zn的高度相關的輸入信號模型,其中zn為均值等于0的高斯白噪聲。從圖4和圖5中可以清楚地看出,相比于傳統的NLMS-OCF算法,NLMS-OCF-IE算法表現出了比較快的收斂速度,尤其是迭代步長為0.1時效果比較明顯。通過與示例1的比較,可從中發現NLMS-OCF-IE算法對于高度相關輸入信號的效果比較顯著。
5 結束語
為了修正NLMS-OCF算法迭代方向上的誤差,我們提出了NLMS-OCF-IE算法,使得迭代方向和引起估計迭代誤差方向相同,從而減小迭代誤差,并將改進的算法在MATLAB中進行仿真,仿真結果表明,NLMS-OCF-IE算法相對于傳統的NLMSOCF算法,不僅減小了誤差,而且還加快了收斂速度,提高了自適應濾波器的性能。
[1]WIDROW B,STEARNS S D.Adaptive signal processing[M].Upper Saddle River,N.J.:Prentice Hall,1985.
[2]HAYKIN S.Adaptive filter theory[M].4th ed.Upper Saddle River,N.J.:Prentice Hall,2002.
[3]SAYED A H.Fundamentals of adaptive filtering[J].Control Systems IEEE,2003,25(4):77-79.
[4]MORGAN D R,KRATZER S.On a class of computationally efficient,rapidlyconverging,generalizedNLMSalgorithms[J].1996,3(8):245-247.
[5]SANKARANSG,BEEXAA.NormalizedLMSalgorithmwith orthogonal correction factors[C]//Asilomar Conference on.IEEE,1997:1670-1673 vol.2.
[6]KIM S E,LEE J W,SONG W J.A Theory on the Convergence Behavior of the Affine Projection Algorithm[J].IEEE Transactions on Signal Processing,2011,59(12):6233-6239.
[7]FAN Y,ZHANG J.Variable step-sizeaffine projection algorithm with exponential smoothing factors[J].Electronics Letters,2009,45(17):911-913.
[8]SANKARAN S G.On ways to improve adaptive filter performance[D].Blacksburg,Virginia,U.S.:Virginia Polytechnic Institute and State University,1999.

