非均勻線陣的互耦自校正

張佳佳, 陸曉飛, 陳 輝, 季正燕

(空軍預警學院一系, 湖北 武漢 430019)

0 引 言

一直以來,均勻線陣(uniform Linear array,ULA)以其陣列結構簡單,陣列流型具有范德蒙德矩陣結構特點備受關注,各種高分辨算法都是基于ULA發展推廣而來的。在陣元間距相等的約束條件下,只要陣元數目確定,陣列孔徑就確定了,分辨力也就確定了。要想提高分辨力只能增加陣元數目,這無疑大大增加了成本,而且還會引起高分辨算法計量的增加,因此為解決這一難題非均勻線陣(non-ULA,NULA)[1-2]應運而生。經過精心設計的NULA能夠滿足在相同陣元數的前提下擁有更大的天線孔徑,進而提高波達方向(direction of arrival, DOA)分辨率。同時,相較于ULA來說,NULA更便于實現,給天線排布方式帶來很大的靈活性。

類似于傳統的ULA,NULA也會受到各種陣列誤差的影響,尤其是陣元間的互耦誤差。幾十年來,涌現出很多互耦誤差自校正方法。例如,文獻[3-4]都是基于子空間的原理,利用互耦矩陣的特殊性,使角度和互耦系數解耦合。此類方法不需要高維非線性搜索,計算量小,但對陣列結構有要求。文獻[5-6]同時運用了陣列結構特點和互耦矩陣的帶狀對稱Toeplitz特性,結合旋轉不變子空間(estimation signal parameters via rotational invariance technique, ESPRIT)算法,將角度和互耦系數分離。此類方法無需先驗知識,也不需要迭代搜索。文獻[7]提出了歸一化空間譜的方法去除部分耦合誘導的虛假峰值,成功提高分辨力,穩健估計信號來向。文獻[8]利用源信號的統計特性,由盲源分離算法估計廣義陣列的陣列流型,而后利用互耦矩陣特性將DOA估計問題轉化為多個可分離的非線性最小二乘問題,此類算法無需高維搜索和迭代,對互耦自由度要求低,穩健性高。文獻[9]針對混合信源DOA估計和互耦誤差校正提出方法。首先根據互耦矩陣特點,粗略估計獨立源的DOA,而后結合斜投影和前后平滑實現DOA估計,最后利用估計的DOA,提出非子空間類的校正方法。近年來,壓縮感知的方法在DOA估計方面得到廣泛應用,研究者們也開始將其運用到陣列誤差的校正上來。文獻[10]采用了貝葉斯的方法聯合估計DOA和互耦系數,充分運用到了互耦矩陣稀疏特性,但過程中仍需要迭代運算,計算量大,估計時間久。然而NULA的互耦矩陣并不具備Toeplitz特性,給NULA互耦誤差自校正帶來了很大的困難。文獻[11]針對NULA中的最小冗余陣,將低秩恢復的思想運用到陣列協方差重構中,解決DOA估計和互耦誤差問題。此方法多次運用近似思想,必然會導致估計精度下降,中間的迭代過程也會使計算量增加。文獻[12]比較3種不同的NULA,針對偶極天線和微帶天線,提出解決互耦誤差的方法。文獻[13]在單快拍情況下針對L型NULA互耦校正提出解決方法。算法推導了不具有內插變換的無互耦協方差矩陣與互耦和內插變換的協方差矩陣之間的近似優化,形成了用于互耦校正和DOA估計的全局優化問題。此方法中需要交替的優化過程計算量大。文獻[14]采用了輔助信源的方法,通過選擇天線構造3個分時發射的校正源,得到3個方位校正數據,聯合估計互耦和幅相誤差。在低信噪比(signal-to-noise ratio,SNR)情況下占優勢,但誤差較大或天線旋轉角度小時算法會失效。同樣，針對NULA的互耦和幅相誤差,文獻[15]不需要校正源,而是利用更一般的線性幾何方法來提高估計能力,方法還可推廣到非均勻圓陣中。

本文主要針對關于中心原點對稱的NULA,解決DOA估計和互耦誤差自校正的問題。通過分析陣列結構,發現此類陣列互耦矩陣具有關于反對角線對稱的特點,可將其分解成2個具有Toeplitz特點的矩陣之差的形式,從而方便實現角度和互耦系數的解耦合,而后結合子空間原理,同時估計信號的DOA和互耦系數。算法可以有效地避免高維搜索和迭代過程,簡化計算量,同時具有精度高、分辨力強的特點,可以有效地解決關于中心陣元對稱的NULA互耦問題。

1 數據模型的建立

1.1 理想情況下NULA的數據模型

一個N=5的NULA位于x軸上,陣元位置為xk(k=1,2,…,5),陣列布局如圖1所示,呈現出根據中心陣元對稱分布的形態,其中d=0.5λ表示距離單元,λ代表波長,將原點處作為參考點。為簡化推導過程,僅考慮現實中方位角的應用情況,方位角為θ∈(-180°,180°)。

圖1 NULA的陣列結構Fig.1 Array structure of NULA

第k個陣元的相位差為

(1)

導向矢量可表示為

a(θ)=exp(-jβk)

(2)

整個陣列的流型矩陣為

A=[a(θ1),a(θ2),…,a(θM)]

(3)

式中,M表示信號源數。則陣列的接收數據可以表示為

X(t)=AS(t)+N(t)

(4)

式中,X(t)為數據矢量;A為理想無誤差時的陣列流型矩陣;S(t)為信號矢量;N(t)為均值為0、方差為δ2的高斯白噪聲(white Gaussian noise, WGN)矢量。

1.2 互耦誤差存在情況下的數據模型

由文獻[16]可知,互耦系數與陣元間距之間存在反比關系。當陣元間距較小時,陣元間的互耦效應強,互耦系數大;當陣元間距大到一定程度導致稀疏,陣元間的互耦效應就很小,互耦系數近似為0。根據文獻[8,17],通常情況下對于線陣來說,存在互耦影響的2個陣元之間距離不會超過2.5λ。因此在本文中,假定當陣元間距大于2.5λ時,2個陣元之間的互耦為0。不同于ULA的等距分布,關于中心陣元對稱的NULA的互耦矩陣不再具有Toeplitz特性,卻具有以下特點:

(1) 由互易原理可知,陣元i對陣元j的互耦效應等于陣元j對陣元i的互耦效應,即

zi,j=zj,i

(5)

(2) 陣元對自身的互耦系數為1,即

zi,j=1,i=j

(6)

(3) 當2個陣元之間的距離大于存在互耦效應的最大距離p1時,互耦系數為0,即

zi,j=0,dij>p1

(7)

(4) 具有相同間距的陣元,互耦系數相同,即

zi,j=z(N+1-i),(N+1-j)

(8)

例如當互耦自由度分別為2和3時,互耦矩陣可以表示為

(9.2)

可以看出,互耦矩陣Z可以分解成兩部分矩陣之差,即有

Z=D-B

(10)

式中,一部分是具有帶狀對稱Toeplitz特性的矩陣D,可以由其第一行元素唯一表征;而另外一部分矩陣B則具有以下特性:

(1) 第1行和最后1行、第1列和最后1列均為0。

(2) 除掉特性(1)中為0的行和列,剩下的矩陣仍具有帶狀對稱的Toeplitz特性。

因此,當互耦存在時,整個陣列的接收數據可表示為

X(t)=ZAS(t)+N(t)

(11)

在快拍數L有限的情況下,陣列協方差矩陣可表示為

(12)

2 互耦自校正算法

2.1 原理描述

設互耦自由度為p,則互耦系數矢量z=[g1,g2,…,gp]T,此時陣列流型矩陣為

[Za(θ1),Za(θ2),…,Za(θM)]

(13)

當互耦存在時,根據子空間原理,多重信號分類(multiple signal classification, MUSIC)算法的譜估計可表示為

(14)

若采用聯合搜索來估計角度和互耦系數,搜索維數由無互耦時的一維變為(p+M-1)維,計算量很大,無法滿足實時處理要求。根據式(10),Z可分解為兩部分之差,則有

Da(θ)-Ba(θ)=T1[a(θ)]z-T2[a(θ)]z

(15)

式中,T1和T2分別代表矩陣D和B所對應的重構矩陣。因矩陣D具有帶狀對稱的Toeplitz特點可知,T1可表示為

T1=Ta+Tb

(16)

(18)

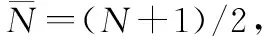
當p=2時

(19)

(20)

(21)

當p=3時

(22)

(23)

(24)

當p=4時

(25)

(26)

(27)

隨著p值的增大,重構矩陣T1和T2的表達式越來越復雜,但他們的表達式是唯一確定的。將得到的T1和T2代入式(15)整理可得

(28)

將式(28)代入式(14)可得

(29)

zHQ(θ)z=0

(30)

很顯然,互耦誤差的存在使得z≠0,那么式(30)成立的條件就是N×p維矩陣Q(θ)出現秩損。當且僅當方位角為真實信號來向時,滿秩矩陣Q(θ)才會變成奇異陣。因此,對信號角度的估計便可由式(31)或式(32)來完成。

(31)

(32)

式中,λmin[·]和det[·]分別為求矩陣最小特征值和矩陣行列式的算子。而后利用角度估計值,結合式(33)進一步估計互耦系數。

(33)

式中,emin[·]表示求矩陣最小特征值對應的特征矢量。

2.2 算法步驟

NULA互耦自校正(self-calibration of mutual coupling for NULA, SCNL)算法的基本步驟如下:

步驟2通過式(16)～式(27)分別獲得相應的重構矩陣T1和T2;

步驟3根據式(28)構造重構矩陣T,并求得Q(θ);

3 仿真分析

一個5元NULA位于x軸上,陣元位置如圖1所示,其中d=0.5λ,λ為波長,噪聲為零均值WGN,在方位角度12°和16°的方位上存在2個非相干信號源。令整個陣列的互耦自由度為p=3,互耦系數矢量為z=[1;0.882 1+0.658 3j;-0.347 6+0.146 9j]。

實驗1NULA互耦校正空間譜圖

當快拍數為300,圖2(a)和圖2(b)分別表示在不同SNR情況下,互耦未知、互耦已知、經典自校正(簡稱WF)算法及本文提出的2種方法的空間譜曲線的比較。

圖2 空間譜圖Fig.2 Spatial spectrum

由仿真結果可以看出,當互耦誤差存在時,普通的MUSIC算法完全失效。WF算法可以估計DOA,但是SNR較小的情況下測得的角度偏離實際值較遠,精度相對較差。而本文提出的SCNLE和SCNLD算法與互耦已知時的MUSIC算法均可以在信號來向處形成一個尖銳的峰值,準確地估計信號的DOA。實驗說明了本文算法的有效性,在SNR較低時,本文算法的性能要優于WF算法。

實驗2角度估計性能分別與SNR和快拍數的關系

當快拍數為300,SNR從0 dB變化到30 dB,間隔2 dB,通過100次蒙特卡羅仿真實驗,比較互耦已知、WF算法、SCNLD算法、SCNLE算法的角度估計性能隨SNR變化的關系。這里限定算法能同時分辨出2個獨立信源,并且估計偏差小于0.5°時視為成功。圖3給出了4種算法成功概率的比較。

圖3 成功概率與SNR的關系Fig.3 Relationship between success probability and SNR

圖4則給出了4種算法均方根誤差(root mean square error, RMSE)隨SNR的變化關系。

圖4 RMSE與SNR的關系Fig.4 Relationship between RMSE and SNR

同理,當SNR為10 dB不變情況下,快拍數從10變化到510,圖5和圖6分別給出了4種算法的成功概率和RMSE隨快拍數變化的關系。

整體來說,SCNLD和SCNLE算法的估計性能相差不大。由圖3和圖5可知,當SNR較低時,本文算法的成功概率低于互耦已知的MUSIC 算法,但明顯優于WF算法,當SNR大于10 dB以后或快拍數大于300,本文算法百分百成功。由圖4和圖6可知,SCNLD和SCNLE算法的RMSE均略大于互耦已知的MUSIC算法的,小于WF算法。

圖5 成功概率與快拍數的關系Fig.5 Relationship between success probability and thenumber of snapshot

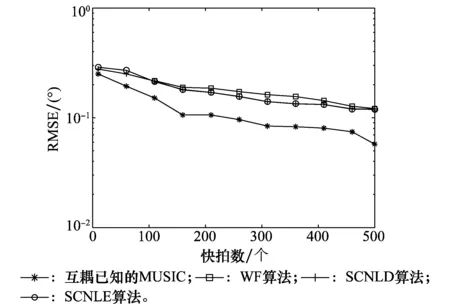
圖6 RMSE與快拍數的關系Fig.6 Relationship between RMSE and the number of snapshot

實驗3互耦系數的估計

本實驗考察了SCNLE算法對互耦系數的估計性能。定義互耦系數矢量的相對校正誤差為

(34)

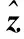
圖7 互耦系數的校正誤差隨SNR變化的關系Fig.7 Relationship between correction error of mutual coupling coefficients and SNR

圖8則表示當SNR為10 dB,快拍數從10到510時,互耦系數的校正誤差隨快拍數的變化。

圖8 互耦系數的校正誤差隨快拍數變化的關系Fig.8 Relationship between correction error of mutual coupling coefficients and the number of snapshot

通過100次蒙特卡羅實驗,表1、表2顯示了在快拍數為300時,不同SNR情況下得到的互耦系數的估計。

表1 互耦系數g2的估計(真值0.882 1+0.658 3j)

表2 互耦系數g3的估計(真值-0.347 6+0.146 9j)

實驗結果表明,隨著SNR的增加,ε值會越來越小。當SNR大于15 dB時,互耦校正誤差趨近0值。同樣,ε也會隨著拍數的增大而逐漸變小,最終趨近0值,說明估計出的互耦系數值十分接近真值。

4 結 論

本文針對關于中心陣元對稱的五元NULA,提出互耦自校正算法。通過對NULA整體結構的分析,發現其互耦矩陣具有關于反對角線對稱的特點,并且可將其分解成2個矩陣之差的形式。其中的一個是具有帶狀對稱Toeplitz特性的矩陣,而另外一個矩陣除掉邊框為0的行和列,也具有Toeplitz矩陣的特性,這樣一來就可以方便地構造出合適的重構矩陣,實現角度和互耦系數的解耦合,而后根據子空間原理,就可實現DOA的估計和互耦系數的求解。本文所提算法不需要額外的輔助陣元和輔助信源,同時可以有效降低搜索的維數,減少運算量,在角度相隔較近的情況下仍然具有較高的估計精度,很好地解決了NULA的互耦問題,具有較大的實際意義。

參考文獻：

[1] KWIZERA E, MWANGI E, KONDITI D B. Direction of arrival estimation based on MUSIC algorithm using uniform and non-uniform linear arrays[J]. Journal of Engineering Research and Application, 2017, 7(3): 51-58.

[2] 張陽,王新民.基于非均勻線性陣列雙遠場信源DOA估計的最小分辨率極限[J].系統工程與科學技術,2017,39(3):465-470.

ZHANG Y, WANG X M. Minimum resolution limit of dual far-field sources DOA estimation with a non-uniform linear array[J]. Systems Engineering and Electronics, 2017, 39(3): 465-470.

[3] LIU K H, ZHENG Z, YANG H F, et al. An approach to robust beamforming in the presence of mutual coupling for uniform linear arrays[C]∥Proc.of the 2nd IEEE International Conference on Computer & Communications, 2017: 1870-1874.

[4] DAI J S, XU B, NAN H, et al. A recursive RARE algorithm for DOA estimation with unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters,2014,13(5):1593-1596.

[5] LI H B, GUO Y D, GONG J, et al. Mutual coupling self-calibration algorithm for uniform linear array based on ESPRIT[C]∥Proc.of the International Conference on Consumer Electronics, 2012: 3323-3326.

[6] LIU S, YANG L S, YANG S Z, et al. Blind direction-of-arrival estimation with uniform circular array in presence of mutual coupling[J]. International Journal of Antennas and Propagation, 2016, 2016(8): 1-7.

[7] CAI S. A normalized spatial spectrum for DOA estimation with uniform linear arrays in the presence of unknown mutual coupling[C]∥Proc.of the International Conference on Acoustics, Speech and Signal Processing, 2016: 3086-3090.

[8] 胡增輝,朱炬波,何峰,等.互耦條件下均勻線陣DOA盲估計[J].電子與信息學報,2012, 34(2): 382-387.

HU Z H, ZHU J B, HE F, et al. Blind DOA estimation in the presence of mutual coupling using uniform linear array[J]. Journal of Electronics & Information Technology, 2012, 34(2): 382-387.

[9] 景小榮,楊洋,張祖凡，等.均勻線陣混合信源DOA估計與互耦誤差自校正[J].系統工程與電子技術,2014,36(9):1696-1701.

JING X R, YANG Y, ZHANG Z F, et al. DOA estimation for mixed signals and mutual coupling self-calibration for uniform linear array[J].Systems Engineering and Electronics,2014,36(9):1696-1701.

[10] WANG Q, DOU T D, CHEN H, et al. Effective block sparse representation algorithm for DOA estimation with unknown mutual coupling[J].IEEE Communications Letters,2017,21(12): 2622-2625.

[11] 曹圣紅. 存在陣列誤差條件下波達方向估計算法研究[D]. 合肥: 中國科學技術大學, 2014.

CAO S H. Direction of arrival estimation algorithms in the presence of array error[D]. Hefei: University of Science and Technology of China, 2014.

[12] BOUDAHER E, AHMAD F, AMIN M G, et al. Mutual coupling effect and compensation in non-uniform arrays for direction-of-arrival estimation[J]. Digital signal processing, 2017, 61(c):3-14.

[13] HOU Y G, ZHANG T Y, WU S C. An optimization estimation for mutual coupling correction of L-shaped nonuniform array with single snapshot[J]. Mathematical Problems in Engineering, 2015, 2015(3): 1-11.

[14] LI W X, LIN J Z, ZHANG Y, et al. Joint calibration algorithm for gain-phase and mutual coupling errors in uniform linear array[J]. Chinese Journal of Aeronautics, 2016, 29(4): 1065-1073.

[15] DAI J S, ZHAO D, YE Z F. DOA estimation and self-calibration algorithm for nonuniform linear array[C]∥Proc.of the International Symposium on Intelligent Signal Processing and Communication Systems, 2010: 1-4.

[16] 王永良,陳輝,彭應寧,等.空間譜估計理論與算法[M].北京:清華大學出版社,2004:392-406.

WANG Y L, CHEN H, PENG Y N, et al. Theory and algorithm of spatial spectrum estimation[M]. Beijing: Tsinghua University Press, 2004:392-406.

[17] DAI J S, XU W C, ZHAO D A. Real-valued DOA estimation for uniform linear array with unknown mutual coupling[J]. Signal Processing, 2012, 92(9): 2056-2065.