基于仿生咀嚼機器人的種植體螺紋結構研究

代 欣，俞經虎，詹民民

（1.江南大學 機械工程學院，無錫 214122；2.江蘇省食品加工技術裝備重點實驗室，無錫 214122）

0 引言

近數十年來，高達90%～95%的牙齒缺失患者選擇以種植牙方式解決口腔問題，這使得口腔種植體受到廣泛的關注和運用[1]。口腔種植修復手術獲得成功的關鍵在于種植體與骨組織能否實現良好的骨結合[2]。雖然一些臨床研究報告中提出種植牙的成功率普遍較高，但是種植牙植入手術的失敗在長期臨床實踐上來說仍舊不可避免[3]。在咀嚼的過程中，種植牙承受壓力過大會導致骨融合缺失，從而導致牙周植入區域的感染和口腔修復手術的失敗。為了避免發生上述情況，關鍵問題在于了解種植牙咀嚼過程中最大應力在何處產生。考慮到骨水平上的應力分布在臨床評估的難度較大，采用有限元方法分析種植體的生物力學性能不可或缺。種植體螺紋結構在口腔種植體生物力學的最優化評價中是一個重要的評估內容[4]，種植牙在咀嚼過程中產生的咀嚼壓力會引起種植牙周圍骨組織界面的改組或重建，改變后的結果對種植牙的壽命和種植成功率有著重要的影響。所以對于臨床試驗的長足發展來講，研究種植牙的力學規律有著深刻的指導意義。

螺紋的幾何結構參數包括螺距、螺紋深度和螺紋形狀[5]。本研究僅分析螺紋形狀，擬在保證種植體的長度、直徑、螺距、螺紋深度、橫截面積等參數完全一致的情況下，改變螺紋形狀并分別對梯形螺紋、支撐形螺紋和反支撐形螺紋進行有限元分析。國內外也有研究人員利用有限元技術對種植牙螺紋結構優化進行了相關研究，楊德圣等[6]提出骨組織類形和螺紋形態都會影響種植體的穩定性，其中支撐形螺紋種植體的穩定性比三角形螺紋好。O.Eraslan[7]等針對四種不同的螺紋結構進行了有限元分析，提出不同的螺紋設計不會影響到支撐骨組織上的應力集中。從上述研究內容可以看出，現有的研究大多將與種植體相連的牙冠簡化處理，并且將作用在種植體上的咀嚼力簡化為軸向和切向作用力，直接給定咀嚼力數值。實驗數據沒有基于真實的咀嚼實驗，也忽略了食物對凹凸不平的牙冠表面作用力的復雜性。本研究擬從實際的咀嚼情況出發，建立真實的牙冠模形，首先通過仿生咀嚼機器人模型進行咀嚼實驗，得出夏威夷果的力-位移曲線。通過力-位移曲線確定施加在牙冠種植體模型上的載荷大小，此舉更加接近真實的咀嚼載荷沖擊效果，并不直接施加不同方向的力作用在牙冠上，而是設置動態的沖擊載荷以一定的初速度和加速度撞擊牙冠-種植體模型，最后得出分析數據并討論結果。本文利用CT掃描成年男子牙冠數據，并通過UG三維繪圖軟件建立三種不同的種植體模型和骨組織模型，利用Hypermesh軟件對三維模型進行網格劃分并采用LSDYNA軟件對種植體和骨組織界面進行力學性能分析。

1 材料和方法

本文利用六自由度仿生咀嚼平臺作為實驗儀器（如圖1所示），模仿人類真實下頜的咀嚼運動，對夏威夷果進行咀嚼過程的力采集，得到咀嚼過程中的咀嚼力與位移的關系曲線。取五次實驗曲線的平均值作為有限元軟件模擬分析的加載條件。

圖1 仿生咀嚼6PSS并聯驅動平臺實體模型

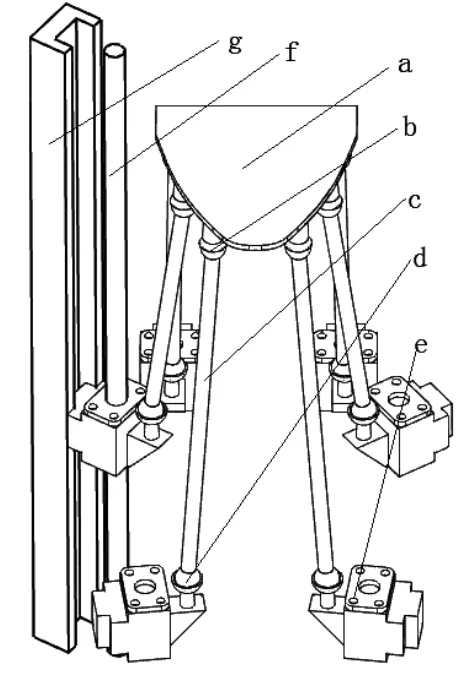
圖2 仿生咀嚼6PSS并聯驅動平臺簡圖

圖2所示給出仿生咀嚼6PSS并聯驅動平臺的機構簡圖，該結構整體沿著YOZ平面對稱，在該圖中，驅動支鏈有6根。模型中驅動支鏈兩兩分為一組，分別模擬下頜系統中的顳肌、咬肌和翼狀肌。每根驅動支鏈由導軌、滾珠絲杠、滑塊組成的移動副、連桿一端與滑塊連接的下球副、連桿另一端與動平臺連接的上球副組成，隨著電機控制絲杠轉動，帶動滑塊移動，通過驅動支鏈實現動平臺的運動。

對于仿生咀嚼平臺樣機進行運動控制，不僅需要各部分硬件相互配合實現位姿變化，同時也需要開發對應的軟件系統來對整個咀嚼機構進行控制，軟件界面及參數設置如圖3所示，采用C++程序對軟件程序進行界面設計，實現下平臺的位置和速度顯示、聯動、停止、二次至多次咀嚼功能，對咀嚼時長、次數、方式和加速度等均可自定義輸入。將夏威夷果放在下頜動平臺上完成咀嚼試驗，通過置于上頜靜平臺頂端的力傳感器采集力數據，得到的力與位移曲線如圖4所示。隨著牙齒的擠壓作用，夏威夷果受力達到400N左右時發生破裂，此后壓力迅速下降，根據人類牙齒的真實使用情況（即正常人類牙齒的咬合力難以咬碎夏威夷果），因而本文設定有限元求解的受載條件為400N的沖擊力。

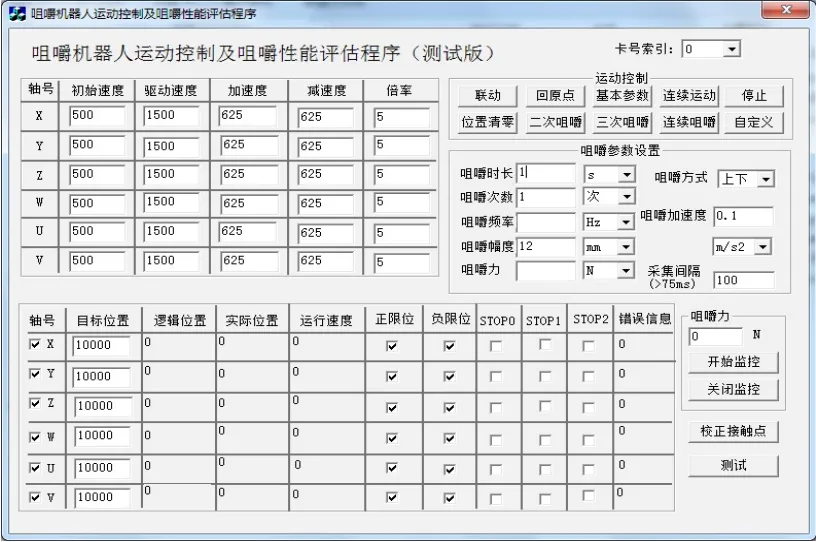
圖3 運動控制程序界面

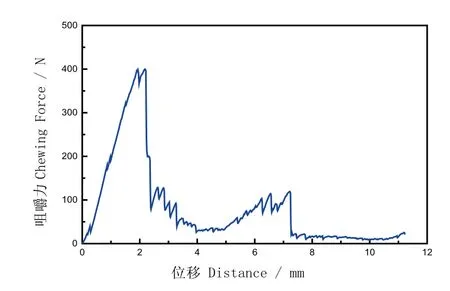
圖4 夏威夷果在仿生咀嚼機器人作用下的力-位移曲線

種植體參考瑞士ITI種植系統建立，將模型分為種植體、基臺、牙冠三部分。骨組織模型模擬人體的下頜骨結構，整體尺寸為20×15×20mm，外部為一層2.00 mm厚的皮質骨，內部為松質骨；牙冠模型借助逆向工程技術得到；種植體如圖5所示，主要建立了梯形、支撐形和反支撐形三種不同的模型，種植體體部直徑為3.75mm，頸部選用常規頸，頸部直徑為4.8mm；種植體螺紋部分長度l3=10.0mm，頜齦距離l1=3.00mm，穿齦高度l2=2.80mm；螺距p=1.25mm，螺高D2=0.40mm，螺深D3=0.35mm。

將幾何模型導入Hypermesh軟件中劃分網格，如圖6所示，考慮到牙冠的不規則性，采用四面體單元。每一個有限元模型大概包含130000個節點和640000個單元。模型的邊界條件如圖7所示，約束骨組織底部所有節點的自由度，在頂部設置一剛性小球模擬咀嚼平臺實驗中的夏威夷果，使其以一定的速度撞擊牙冠，模擬咀嚼過程中產生的沖擊力。

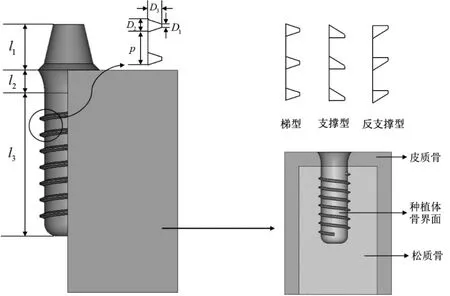
圖5 種植系統模擬配置示意圖

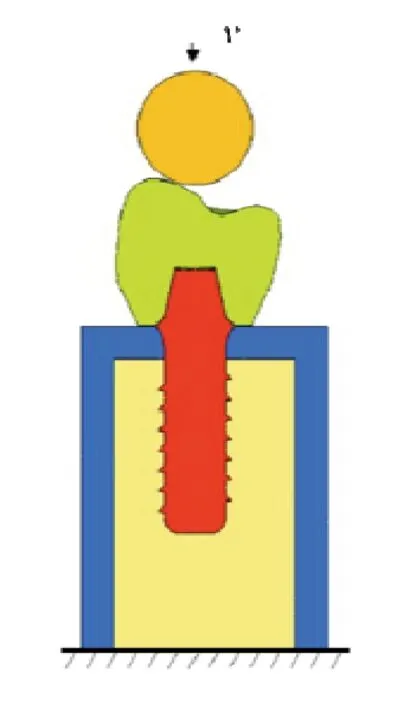
圖7 邊界條件及受載示意圖

有限元模型的材料均簡化為各向同性的彈性材料模型，各部分材料的力學參數（楊氏模量E和泊松比μ翻閱文獻獲得）如表1所示。

2 結果與討論

對于三種不同螺紋形狀的種植體有限元分析結果，采用Von-Mises應力和應變作為主要的評價標準。有限元分析結果表明，有限元模型的最大應力集中出現在種植體的頸部區域和靠近種植體頸部的皮質骨區域上，松質骨上應力分布程度較低并且大多集中在種植體底部區域。這也表明皮質骨的應力集中值比松質骨的應力集中值高。

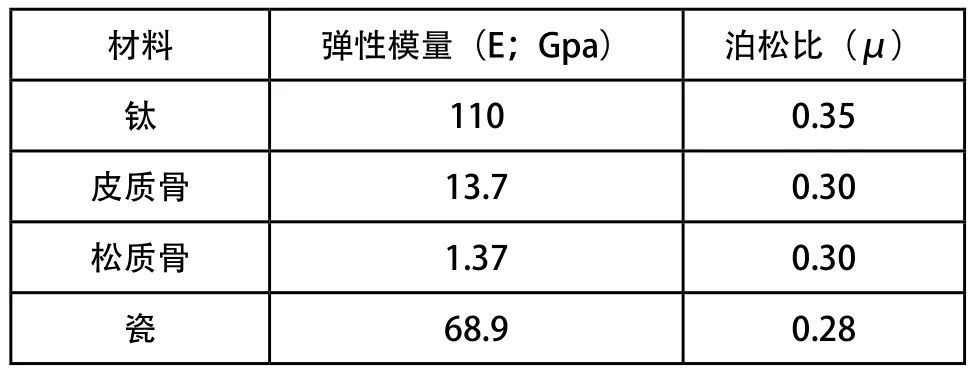
表1 材料的力學性能參數

當剛性小球撞擊牙冠的沖擊載荷大小達到400N時，不同螺紋的種植體模型中的應力分布模式是一致的，但是不同螺紋的Von-Mises應力值大小不同：梯形螺紋的最大應力值是242.8MPa，如圖8(a)所示，支撐形螺紋的最大應力值是278.8MPa，如圖9(a)所示，反支撐形螺紋的最大應力值是253.3MPa，如圖10(a)所示。種植體的最大應力值出現在穿齦部分的頸部區域，螺紋由上至下應力逐漸減小，骨組織中的最大應力值出現在皮質骨頸部區域。種植體中的應變分布模式與應力分布模式類似，在受到同等載荷的作用下，梯形螺紋的應變峰值最小，支撐形螺紋的應變峰值最大。

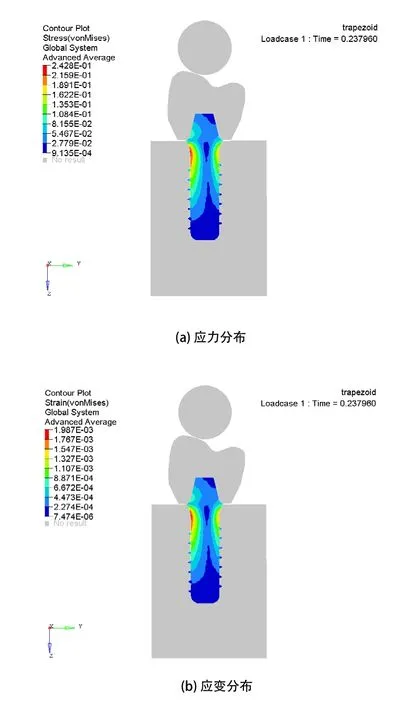
圖8 載荷400N下的梯形螺紋的應力應變分布

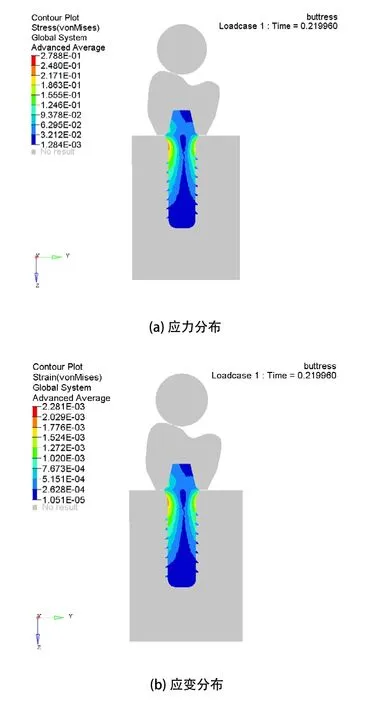
圖9 載荷400N下的支撐形螺紋的應力應變分布

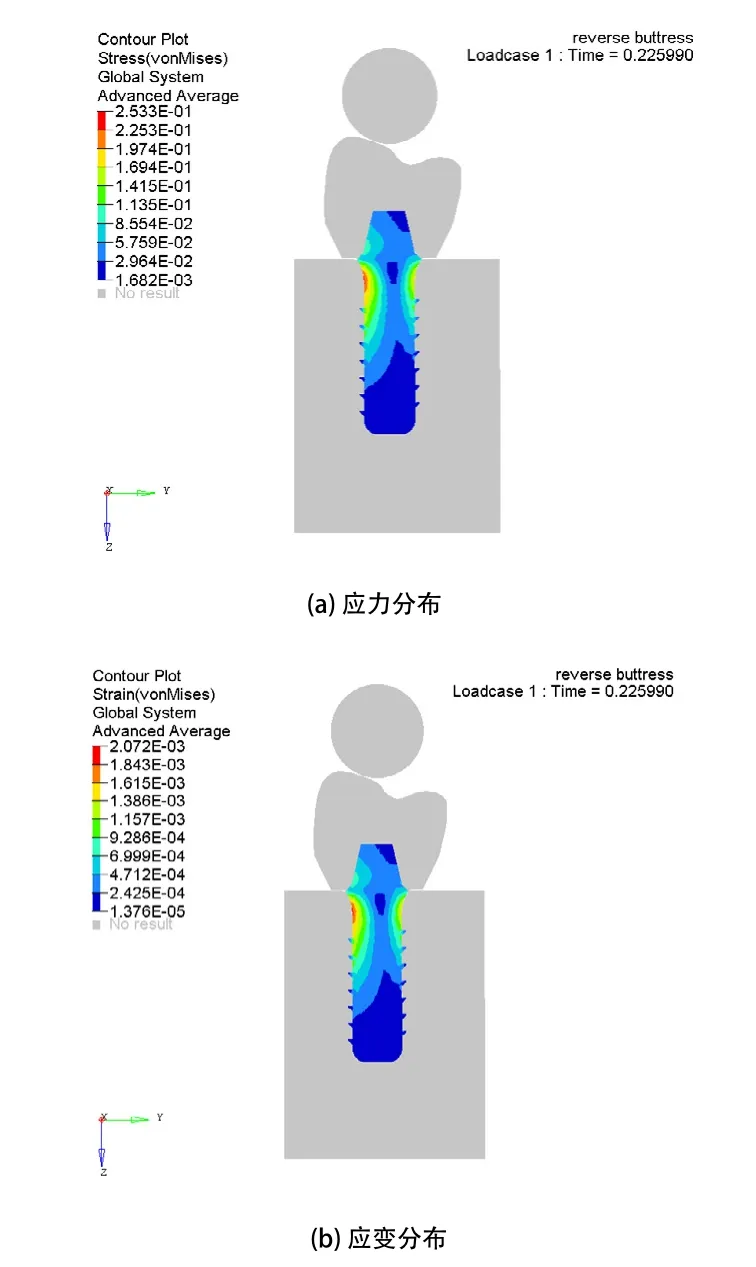
圖10 載荷400N下的反支撐形螺紋的應力應變分布

分別觀察皮質骨和松質骨的橫截面視圖，可以發現普遍情況下皮質骨的應力分布比松質骨的應力分布高；并且皮質骨區第一道螺紋附近骨組織的應力分布比其他道螺紋的應力要高。當評估種植體周邊骨組織上的應力值時（圖11～圖13），最大的應力值是145.1MPa，出現在反支撐形螺紋周圍的皮質骨上。應力分布區域的面積在三種螺紋形狀中基本相當，松質骨中的集中應力主要出現在靠近底部的螺紋區域和種植體骨界面的底部區域。

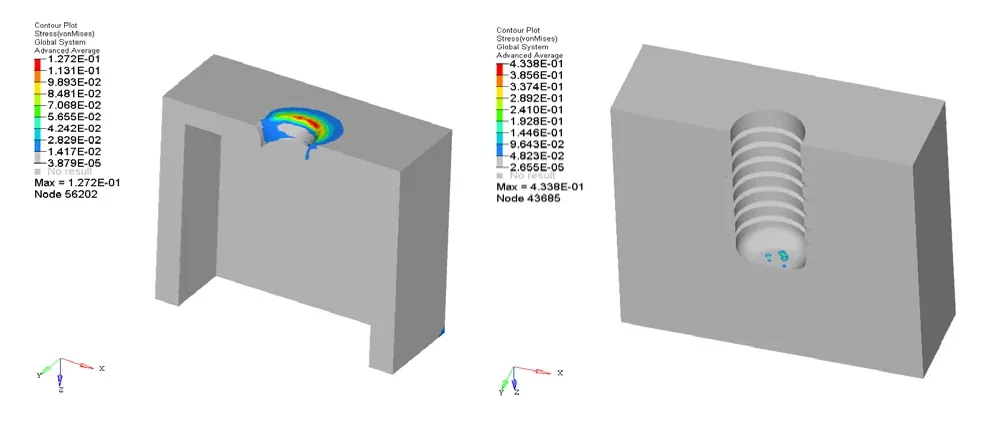
圖11 載荷400N下梯形螺紋的皮質骨和松質骨的應力分布

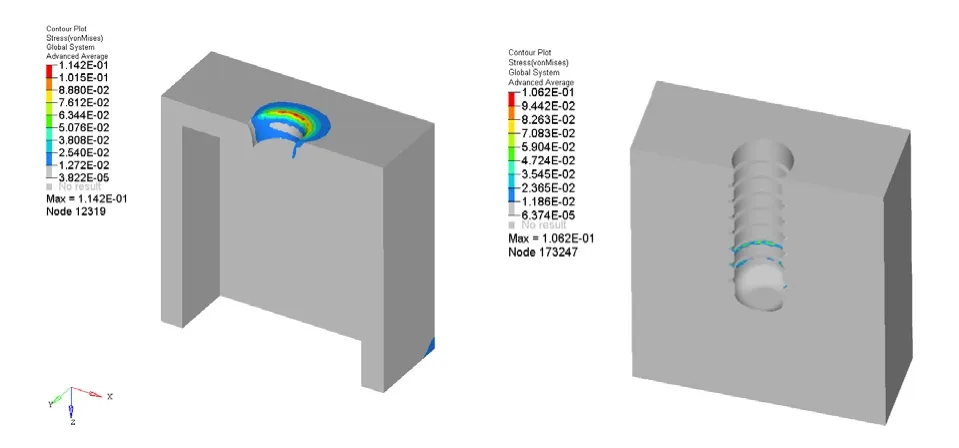
圖12 載荷400N下支撐形螺紋的皮質骨和松質骨的應力分布

圖13 載荷400N下反支撐形螺紋的皮質骨和松質骨的應力分布

到目前為止，國內外對于種植牙的幾何設計還沒有形成普遍共識。種植牙系統的設計目標是優化各項幾何參數來控制生物力學載荷[8]。在實現理想的臨床效果之前，理論研究應該盡量在基于咀嚼實驗的基礎上提供對種植體力學性能的可靠預測，鑒于種植牙臨床實驗的局限性和可行性，有限元分析成為評估種植體系統設計的一個合適工具。本研究采用UG軟件、CT成像技術和有限元分析方法模擬了三種不同的種植體螺紋形狀，結果表明，盡管三種不同螺紋中種植體的Von-Mises應力分布模式類似，但是在相同載荷作用下，梯形螺紋的應力峰值最小，反支撐形螺紋的應力峰值最大。應變分析結果與應力分析結果一致。在骨組織水平上，不同的螺紋應力分布模式類似，但是支撐形的骨組織應力峰值最小，反支撐形螺紋的骨組織應力峰值最大，與種植體上的結果不一致。另外皮質骨的應力集中也明顯高于松質骨，因此推測在種植體中的骨組織缺失將主要體現在皮質骨區域。

以往的研究表明應力集中主要分布在種植體周圍的皮質骨頸部區域并且最高的應力集中值出現在種植體的第一道螺紋周圍的下頜骨區域中[9]。目前的有限元研究也證實了應力集中主要出現在種植體的頸部區域和第一道螺紋周圍。此結果表明壓應力可能就是造成骨組織缺失并引起種植體疲勞失效的一個重要原因[10]，并且在以往研究中證明種植體交界面過高的剪切應力[11]和不充足的機械刺激也是口腔臨床中臨界骨缺失的一個主要原因[12]。在此次有限元研究當中，支撐形螺紋的種植體部分集中應力值最大，但頸部皮質骨區域的應力集中值最小；反支撐形種植體的頸部皮質骨區域的應力集中值最小，但是種植體本身的應力集中值過大，因此綜合考慮整個下頜種植體-骨組織模型的受力情況，螺紋設計成梯形形式會在最大程度上延長種植體的臨床壽命和減小骨組織受到的機械刺激，以期達到最優的種植效果。

3 結論

本文研究了沖擊載荷下不同種植體的應力分布情況，得出了以下結論：

1）不同的種植體螺紋形狀不會影響支撐骨結構中的Von-Mises應力分布模式：種植體的最大應力出現在頸部穿齦部分，螺紋部分的最大應力出現在第一道螺紋附近；

2）種植體的螺紋形狀顯著影響骨界面的應力集中程度，支撐形螺紋對骨組織的作用應力最小，梯形螺紋次之，反支撐形螺紋集中應力最大；

3）皮質骨應力集中區域出現在種植體頸部周圍，松質骨應力集中區域大多集中在靠底部螺紋附近和種植體底部區域，并且皮質骨明顯比松質骨承受更多的集中應力。

本文在已有研究的基礎之上采用真實牙冠模形模擬咀嚼沖擊力，但是針對模形中的下頜組織、材料特性做了一定的簡化，具有一定的局限性。如何更好的模擬口腔環境和更深入全面的進行種植體力學性能研究仍是下一階段的關鍵問題。

[1]Mao Z. Design of dental implant system by FEA[A].Electronics,Computer and Applications, 2014 IEEE Workshop on.IEEE[C].2014:675-677.

[2]Gon?alves W,Adelino V,Bar?o R, et al. 3 FEA in Dentistry:A Useful Tool to Investigate the Biomechanical Behavior of Implant Supported Prosthesis[M].Finite Element Analysis - From Biomedical Applications to Industrial Developments.2013.

[3]Takanobu H, Maruyama T,Takanishi A, et al. Mouth opening and closing training with 6-DOF parallel robot[A].the 2000 IEEE International Conference on Robotics and Automation[C].San Francisco, April 2000:1384-1389.

[4]趙吉奎.牙種植體系統的生物力學有限元分析[D].東北大學,2012.

[5]Brunski J B. In vivo bone response to biomechanical loading at the bone/dental-implant interface[J].Advances in Dental Research,1999,13(1):99.

[6]Schmitter M.Dental implant prosthetics[J].Journal of Prosthodontics,2005,14(3):1-1.

[7]楊德圣,劉洪臣,董軍,等.骨質量和種植體螺紋對種植穩定性影響的三維有限元分析[J].口腔頜面修復學雜志,2005,6(2):118-120.

[8]Eraslan O, Inan O. The effect of thread design on stress distribution in a solid screw implant: a 3D finite element analysis.[J]. Clinical Oral Investigations,2010,14(4):411-416.

[9]Sevimay M, Usumez A, Eskitascioglu G. The influence of various occlusal materials on stresses transferred to implant-supported prostheses and supporting bone: a three-dimensional finite-element study[J]. Journal of Biomedical Materials Research Part B Applied Biomaterials,2005,73(1):140.

[10]李洪友,石茂林,彭云峰.種植牙組件材料力學參數對骨組織接觸應力的影響[J].廈門大學學報(自然版),2015,54(3):409-415.

[11]Duse D M, Pasa A. Dental implants mechanical properties: FEA vs. Physical testing[J]. Annals of Daaam & Proceedings,2011.

[12]Pierrisnard L, Bohin F, Renault P, et al. Corono-radicular reconstruction of pulpless teeth: a mechanical study using finite element analysis[J].Journal of Prosthetic Dentistry, 2002,88(4):442.

[13]Hansson S, Werke M. The implant thread as a retention element in cortical bone: the effect of thread size and thread profile: a finite element study[J].Journal of Biomechanics,2003,36(9):1247.