內化推理策略 提升思維品質
——以“簡單推理——數獨”的教學為例

浙江杭州市蕭山區樓塔鎮中心小學（311200）

數獨是一種需要玩家根據方格內已知的數，利用規則，推理出所有剩余空格的數的填數游戲。這種游戲十分考驗解答者的觀察力和邏輯推理能力。本文以“簡單推理——數獨”（人教版教材二年級下冊第110頁）的教學為例，談談自己的感悟。

一、初次嘗試

我上課前的想法是讓學生掌握好解決數獨問題的一般步驟與方法，并加以拓展應用，從而鞏固推理的知識，感受推理的作用，培養學生解決問題、有序思考的能力，進而提升學生的思維品質。

第一次試教時，我處處圍繞“掌握解決數獨問題的方法”來教，引導學生根據填數規則“（1）每行、每列都有1～4這四個數；（2）每個數在每行、每列中只出現一次。”來解決四個☆處填幾的數獨問題（如圖1），依此形成解決數獨問題的策略。

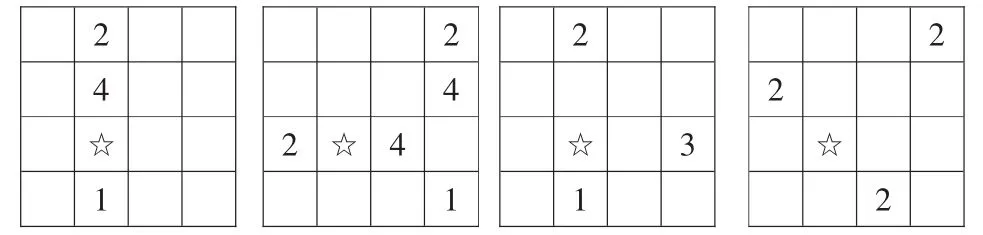
圖1

嘗試應用環節以同桌兩人合作學習的形式，借助上一環節中形成的解決數獨問題的策略，先確定圖2中☆處填幾，最后把整個方格圖填寫完整，從而深化解決數獨問題的策略。

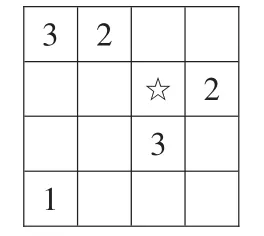
圖2

圖3

鞏固練習環節，學生根據已掌握的解決這類問題的策略，先獨立解決圖3所示的數獨，再同桌交流，最后班級匯報，達到對這種策略的強化和鞏固。

整節課存在以下幾個問題：

問題一：整節課中，都是我帶領著學生學習如何解決具體的數獨問題，學生處于被動學習的狀態，自然不會積極思考問題。

問題二：整節課中，部分學生跟不上教學節奏，教學不能照顧到接受能力較弱的學生。

問題三：很多時候，學生雖然知道☆處填幾，卻不能較好地表述自己的推理過程。

問題四：數獨，既然是數學游戲，那么該節課的游戲味應有所體現。

帶著這些問題，我對該課進行了深入思考，并確定了該課教學的主方向：讓學生自創學習素材，并在完善學習素材的過程中，內化推理策略，提升思維品質。

二、再次實踐

（一）問題指引，形成學習素材

師（出示圖4）：誰能來介紹一下這個圖形？把1、2、3、4這四個數填入16個小方格中的任意四個位置，你會嗎？請在方格紙上用你喜歡的方法填完。

【設計意圖：通過以上兩個問題的指引，既復習了“行和列”的知識，又為新課教學提供了來自學生自身創作的學習素材。】

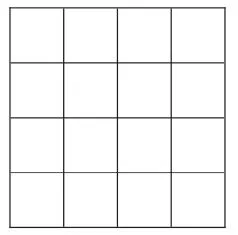
圖4

（二）嘗試完善，獲得推理策略

1.認識規則

師（出示學生作品一，如圖5）：這位同學已經把第一行填好了，接下去需要把余下的三行填寫完整。不過填的時候，需要滿足兩個規則：（1）每行、每列都有1～4這四個數；（2）每個數在每行、每列中只出現一次。

師：誰能用自己的話來介紹一下這兩個規則？

【設計意圖：對填數規則有一個明晰的了解，這對學生后期解決這類問題能起到極大的促進作用，同時有利于指引學生完成該類問題后進行快速檢驗。】

2.完成第二行——應用填數規則

師：根據這兩個規則，第二行可以怎樣填？

生1：2、1、4、3。（如圖 6）

師：你是怎么想的？

生1：只需要和第一行（對應方格）不一樣就行了。

師：還可以怎樣填？

【設計意圖：該環節是借助規則直接填數，只為讓學生再次認識填數規則，并為第三行的填寫埋下伏筆。】

3.完成第三行——獲得推理策略

師：第三行第一個方格，可以填幾？

生2：3。

師：接下去，這行的第二個方格可以填幾？

生3：可以填4。上面已經有了2和1，左邊也有了一個3，所以只能填4。

師：是的，你觀察得很仔細。我們不僅要觀察列中出現的數，還要觀察行中出現的數。你的回答體現了解決這類數學問題的一個很重要的推理策略：當空格所在的行和列中出現了三個不同的數，它里面只能填剩下的那個數。

圖5

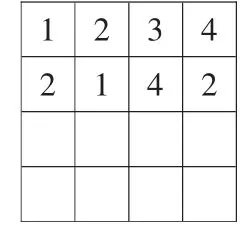
圖6

圖7

師：請大家齊讀這個策略，然后說說這個策略中哪幾個字最關鍵。

生4：三個不同的數。

師：是的，這個策略中最關鍵的就是“三個不同的數”，它是確定一個位置填什么數的關鍵信息。我們可以結合這個策略來描述推理過程。因為它所在的行和列中已經出現了 3、2、1，所以只能填 4。

師：如果第一個方格中填4，那么第二個方格又該怎么填？

【設計意圖：第三行第二個方格的填寫，蘊藏著解決本類問題的關鍵推理策略——“唯一”解法；又因“語言是思維的外殼”，學生能夠清楚地表述推理過程，就能形成思維的邏輯性，所以課堂上不僅要注重推理策略的形成，而且要注重能夠利用推理策略表述推理的過程。】

4.完成第四行——運用推理策略

師：現在只剩第四行了，我們可以怎么填？誰來填？

生5：因為每一列都出現了3個不同的數，所以只能填 4、3、2、1。

5.驗證作品——小結填數策略

師：我們已經把這位同學的作品補充完整了，接下來請同學們驗證每行、每列是否符合規則要求。

師：我們不僅正確地把方格圖補充完整了，還發現了一個解決這類問題的一個關鍵的推理策略，請同學們一起讀一讀。

【設計意圖：完成一個問題后，能回過頭去驗證是一個很重要的學習習慣，這樣能夠幫助學生確認解答的合理性和正確性。在小結環節中，特意引導學生驗證，并再次強調推理策略，既幫助學生內化推理策略，又培養了學生良好的解題習慣。】

（三）合作解決，鞏固推理策略

師（出示學生作品二，如圖7）：這位同學是斜著填的。誰能根據剛才的兩個規則把第一行或第一列補充完整？

圖7

圖8

生6：填第一列 3、4、2。（如圖 8）

師：接下去哪幾個位置可以利用剛才的推理策略優先確定？請把能優先確定的位置圈出來。

圖9

師：是的，這三個位置所在的行和列中都出現了三個不同的數，所以能優先確定。接下來，又能優先確定哪幾個位置？

圖10

師：看來，這個策略在解決這類填數問題時能為我們提供很大的幫助。

【設計意圖：“唯一解法”是解決數獨問題的一種重要推理策略，而這一策略是需要學生在實際應用的過程中逐漸認識并掌握的。利用推理策略找出能優先確定的位置，使得學生對這一策略能有進一步的認識。】

（四）學生創問，同桌交換解答

1.學生創問

師：剛才我們解決了好多填數問題，請自己創造一個問題，讓你的同桌來解決。

師：請在4×4方格紙中，挑選一些空格填上數，然后交由你的同桌把余下的空格填充完整。

2.作品展示

師（出示圖11）：請大家一起來驗證這位同學的作品是否符合規則。

圖11

師：這位同學的作品中不光每行、每列，而且每個2×2小正方形中都有1～4這四個數。

3.錯例辨析

師（出示圖12）：老師發現有一位同學填不下去了，你們認為是什么原因造成的?

師：一開始的問題是怎么樣的？老師把它圈出來（如圖 13）。

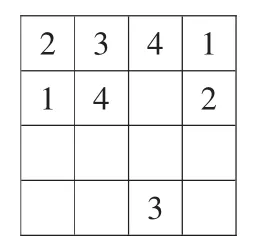
圖12

圖13

師：第二行第三列所在的空格，還能填嗎？

師：在設計問題的時候，需要考慮到填數規則。

【設計意圖：讓學生經歷自己創造問題、同桌互換解決的過程，學生既能感受到數獨游戲的樂趣，又能在錯例辨析中進一步認識到數獨游戲的特點。】

（五）拓展提升，內化推理策略

師（出示問題：把我、愛、數、學這四個字填入方格圖中（如圖 14）。（1）每行、每列都有我、愛、數、學這四個字；（2）每個字在每行、每列中都只出現一次；（3）每個粗線框內都要有我、愛、數、學這四個字。）：這三個規則大家看得明白嗎？誰能來解釋第三個規則?

師：這個問題怎么解決？

圖14

【設計意圖：根據二年級學生的年齡特征，設計了變式練習的運用環節，由此可以使學生進一步掌握解決這類問題的推理策略，也進一步培養學生有序、全面思考問題的意識。】

三、課后感悟

1.重視學生的思維形成過程

試教時，我都是領著學生學習如何解決一個個特定的數獨問題，學生處于被動的學習狀態，根本不會積極思考問題，提升學生的思維品質也就無從談起。

改進之后的再次實踐中，把解決這類數獨問題的策略藏身于學生自主完善方格圖的過程中，通過學生的自主發現“列中已經有了2和1，行中有了一個3，所以只能填4”引出該策略，接著在后面環節中深化與鞏固，并引導學生用語言表述出推理過程，這樣一個推理策略的呈現流程符合學生的認知過程和思維形成過程，不但內化了推理策略，還提升了學生的思維品質。

“語言是思維的外殼”，能夠用自己的語言清楚地表達出推理過程，就能有效地培養思維的邏輯性。因此，教師不僅要注重推理策略的形成，還要注重學生利用推理策略表述推理的過程。

2.注視學習素材的呈現形式

學習素材的呈現，可以來自教材，也可以來自學生自身的創造，而后一種呈現形式更能夠調動學生的學習興趣。第二次教學實踐中，先將學生一開始完成的作品“把1、2、3、4這四個數填入16個小方格中的任意四個位置”作為學習素材組織新課教學，接著對該作品進行完善，引出推理策略，到之后的“學生創問，同桌互換解答”，整節課都是借助學生的作品進行新課教學，十分貼近學生。

在“學生創問，同桌互換解答”這一環節中，讓學生既能感受到數獨游戲的樂趣，又能在錯例辨析中進一步認識到數獨游戲的特點。

3.珍視學生把握規則的能力

每一個數獨問題，都有與之相對應的填數規則，學生是否能夠準確地了解這些規則，是解決數獨問題的首要條件。為此，需要引導學生準確掌握填數規則，運用推理的知識，把握關鍵信息，找出每個數字的確切位置。

在變式練習時呈現前面問題中沒有出現過的第三個規則“每個粗線框內都要有我、愛、數、學這四個字”，使學生進一步掌握解決這類問題的推理策略，也進一步培養他們有序、全面思考問題的意識。