淺談學生數學有序思考能力的培養
廣東江門市新會區會城倫文鉅小學(529100)
小學生正處于數學思維的啟蒙階段,其思維品質的形成對后續的學習有重要影響,因此,教師加強對小學生有序思考能力的培養就顯得尤為重要。
一、有序思考能力的培養要加強方法指導
思維方法的形成離不開引導與強化。在日常教學中,教師應遵循由淺入深、由簡到繁的原則對學生進行系統指導,使學生能逐步按照一定的順序與步驟進行有條理地思考。
例如,教學“數的組成”時,教師可設計如下兩組練習,幫助學生直觀領會“如何進行有序思考”。練習一:把4個蘋果分給甲、乙兩人,可以怎樣分?如果學生缺乏有序思考能力,那他們對這個問題的回答是散亂、無序的。針對這種情況,教師要引導學生一邊操作學具一邊思考:先分給甲1個蘋果,分給乙3個蘋果;然后依次從乙處拿出1個、2個、3個蘋果給甲。學生由此得出三種分法:甲1個,乙3個;甲2個,乙2個;甲3個,乙1個。練習二:寫出得數是6的加法算式,比一比誰寫得多。一部分學生的第一反應是想到什么就寫什么,基本還是無序思考的方式,但也有部分學生略加思考,就能按順序書寫算式。此時,教師可讓學生在小組互助學習中理解并掌握有序思考的方法,同時感受到有序思考具有不重復、不遺漏的效果。
二、有序思考能力的培養可適時借助“工具”
低年級學生的觀察能力和知識運用能力不強,當問題出現較多數據時,學生往往無所適從。對此,教師借助一定的“工具”,便可以幫助學生理清思路,弄清問題的本質,從而讓學生更有效地理解并運用知識。
筆者曾參加二年級“搭配(一)”一課的研討活動。上課伊始,教師首先出示例題:只能用1、2、3這三個數組兩位數,且不能組成11、22之類的數,接著讓兩名學生講講想到了哪些兩位數。由于學生全無準備,因此他們的答案雜亂無序,并出現了遺漏、重復的現象。為了糾正學生雜亂無章的答案,教師引導學生“一組一組地組數”。但實際上,部分學生還未真正理解怎樣“一組一組地組數”,因此組數時并不能做到有序思考。在課后的研討中,筆者建議該教師使用“工具”——括號(或方框)。例如,將數據以(12,21)、(13,31)、(23,32)的形式呈現給學生,這樣可以直觀地把若干數據進行分組,從而幫助學生清晰地認識何為“一組一組地組數”。在之后的二次教學中,此方法果然奏效,學生的答案基本都是有序的。看來,思維訓練不能光靠一些既成的結論,有時還需根據學生的現場生成,為他們提供一些直觀的“工具”(如括號、方框),只有這樣才更利于學生理解和掌握相關知識。
三、有序思考能力的培養需注意方法優化
教師可以在學生進行有序思考的基礎上,引導他們優化解決方案,從而有效促進其思維能力的發展。
例如,例題:用載重量2噸和載重量3噸的車運8噸煤,如果每次每輛車都裝滿,怎樣安排才能恰好運完?對于該題,教師若任由學生隨意列式,最容易出現的情況是學生只考慮到最直接的方案:用2噸的車運4次,因為8÷2=4(次)。這時,教師就需要提醒學生是否還有其他的方案,并引導學生借助表格羅列出不同的方案,再甄別符合題意的方案(如表1和表2)。
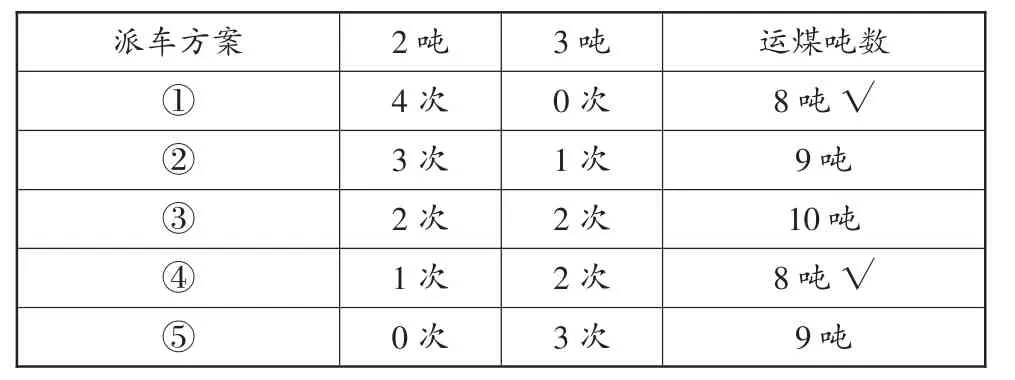
表1
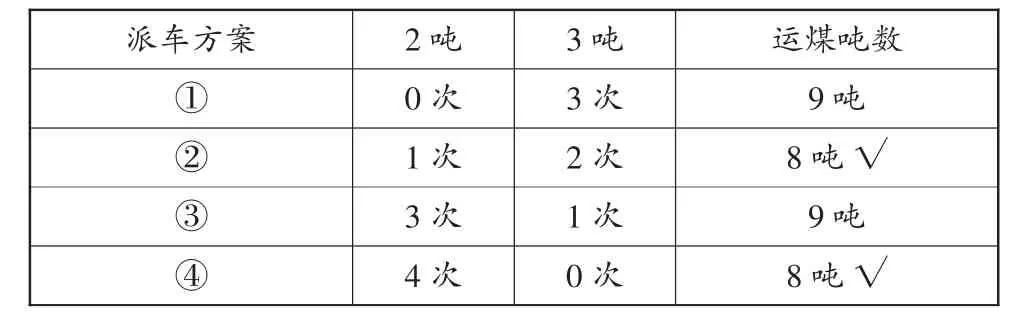
表2
相比之下,表2的思考方法更簡潔一些。當然,利用“數的奇偶性”,本題有更便捷的解題方法:如果同時用兩種車,2噸的車無論運多少次,其運煤總數肯定是一個偶數,則3噸的車運煤總數也必須是偶數,才能滿足總噸數是8噸的要求。因此要滿足3噸的車運煤總數是偶數,其運載次數只能是2次或0次,相應地,2噸的車運1次或4次。
培養學生的有序思考能力,既能使學生思考問題時更有條理,又能做到不重復、不遺漏。教師要有意識地加強學生的思維訓練,培養學生良好的思維習慣,優化學生的思維過程,提高學生的思維敏捷性,從而使學生的數學思維能力得到充分的發展。

