某轎車裝配車間物流緩存區布局優化

（四川大學 商學院 工業工程系，四川 成都 610065）

1 引言

物流緩存區作為制造系統的重要物流設施，主要從事大部分零部件的拆箱、揀選、配貨和送貨上線等作業。物流緩存區的科學合理布局，可以有效加快物料流動速度，同時降低物流強度，節省空間，節約10%-30%的物料運輸費用，為企業贏得競爭優勢。所以，研究制造業物流緩存區的布局優化問題具有重要的理論意義和應用價值。

2 布局優化模型和算法分析研究

2.1 問題描述

本文將物流緩存區的布局問題描述為:在物流緩存區的若干尺寸和上下游產線的若干尺寸已知的條件下，以各作業單位間的總物流最小和作業單位之間實際關聯度與理論關聯度之間的方差最小為目標，建立布局優化模型。

2.2 布局優化問題數學模型的建立

影響生產系統布局的約束條件[1]主要有：

（1）間距約束：圖1為作業單位i與作業單位j之間的相對位置關系示意圖。圖中（xi，yi）為作業單位i的中心坐標；li，wi為作業單位i在X方向和Y方向上的寬度；dxij，dyij為作業單位i與作業單位j在X方向和Y方向上的最小距離。

由圖2-1可得，該約束可表示為公式（1）和公式（2）：

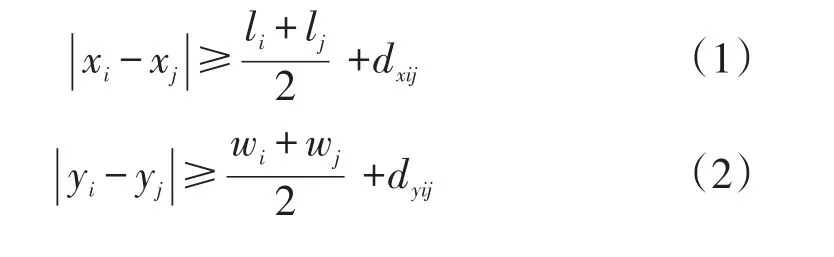
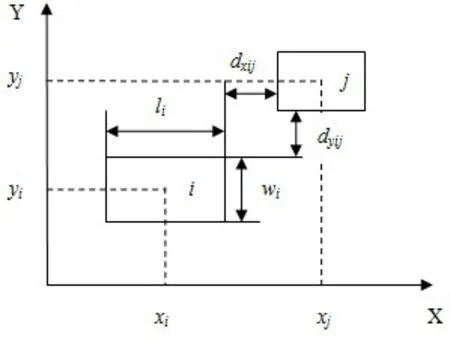
圖1 各個作業單位間的相對位置關系

（2）邊界約束：每個作業單位在X方向和Y方向上的布局不能超過車間的長寬尺寸。L、W為整個布局面積的總長度和總寬度。

該約束表示為公式（3）和（4）：

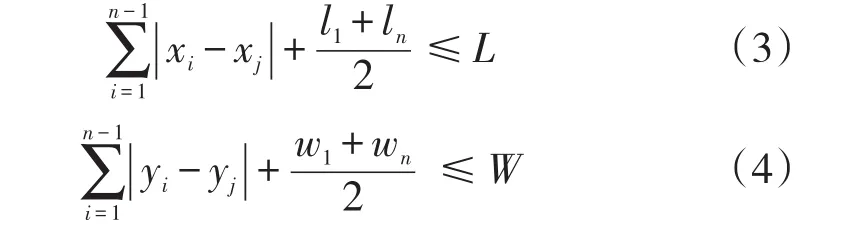
2.3 布局優化問題數學模型

目標函數為公式（5）：

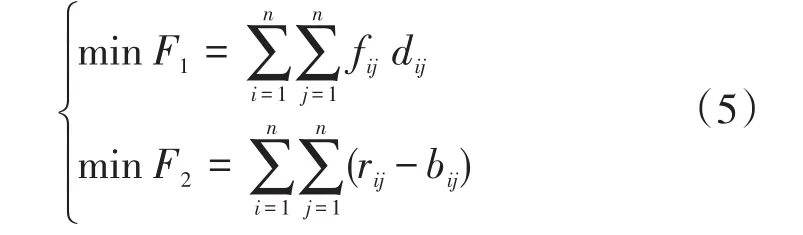
約束條件為（6）：

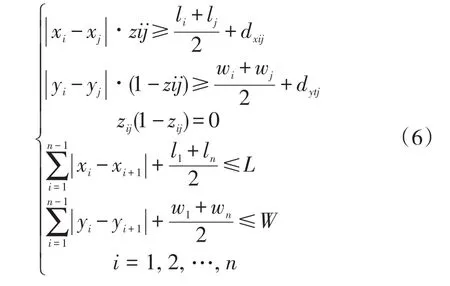
式中：

F1：各個作業單位之間總物流量函數；

F2：各個作業單位之間實際關聯度與理論關聯度之間的方差函數；

n：作業單位的個數；

fij：作業單位i與作業單位j之間的物流量；

dij：作業單位i與作業單位j之間的幾何距離（即曼哈頓距離），如公式（7）所示：

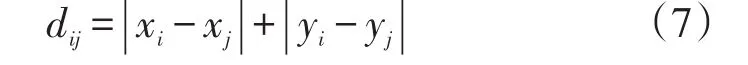
rij：作業單位i與作業單位j之間的理論綜合關聯度；依據系統布局設計程序（SLP），將作業單位間物流的相互關系與非物流的相互關系進行合并，得到rij的量化值見表1。

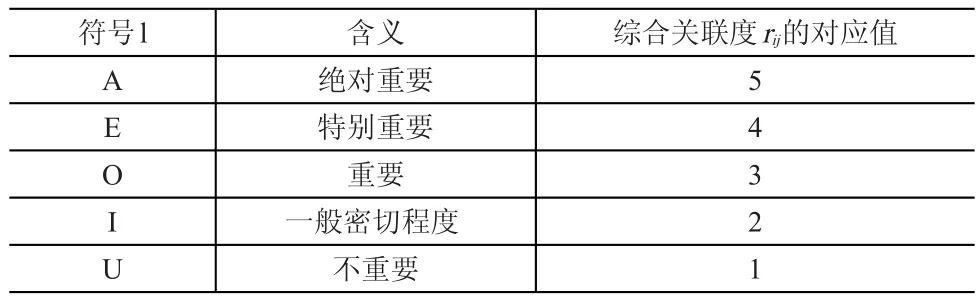
表1 Rij量化值

特別定義當i=j時，rij=0；

bij：作業單位i與作業單位j之間的實際關聯度，其值由作業單位i與作業單位j之間的實際距離dij和最大可能距離dmax決定；bij的值見表2，當i=j時，即為同一個作業單位，dij=0。

表2 關聯因子

zij：0-1整數，由約束3來保證約束1和約束2只有一個表達式有效；xi，yi：作業單位 i的中心坐標；li：作業單位i在X方向上的寬度；wi：作業單位i在Y方向上的寬度；dxij，dyij：作業單位i與作業單位 j在X 方向和Y方向上的最小距離；L：整個布局面積的總長度；W：整個布局面積的總寬度。

2.4 基于遺傳算法的布局優化算法

（1）基于遺傳算法的布局優化算法[2]的設計。可以假設各個作業單位的形狀均為矩形。根據各個作業單位在車間的相對位置關系，設計成對的染色體，分別表示水平約束和垂直約束。例如：染色體1：lpopulation=[……,a,b……]表示矩形a在矩形b的左面；染色體2：wpopulation=[……,a,b……]表示矩形a在矩形b的下面；由此，用1，2，…，n表示各個作業單位，那么由lpopulation和wpopulation來表示布局優化問題的空間解。那么得到的布局效果如圖2所示。

（2）基于遺傳算法的布局優化算法的實現。使用MATLAB軟件進行編程，算法步驟：

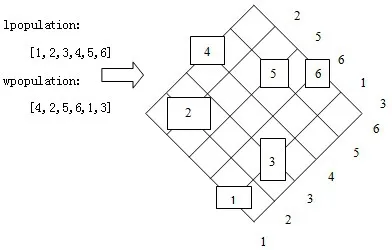
圖2 編碼效果

Step 1:輸入作業單位數N、各作業單位的長寬、車間的總長寬、作業單位間相關度rij；

Step 2:使用自然數編碼，隨機產生初始群體；

Step 3:判斷停止條件，如滿足停止條件，跳到Step 9；

Step 4:計算種群中每一個染色體的適應度值；

Step 5:根據適應度值，隨機選擇一些染色體構成一個新種群；

Step 6:以交叉概率Pc和設計的交叉方法進行交叉運算；

Step 7:以變異概率Pm和設計的變異方法進行變異運算；

Step 8:計算群體中適應度值最大的個體及其適應度值，返回Step 3；

Step 9:輸出種群中適應度值最優的染色體作為問題的最優解。

流程如圖3所示。

3 轎車總裝車間物流緩沖區布局優化[3]

3.1 原型概述

某知名品牌汽車公司成都分公司其車間總面積為4 590m2，其中物流緩沖區為1 220m2，占整個車間面積的22.2%，使用手推車進行物料搬運。

3.2 數據采集與統計

該總裝車間的區域名稱、代碼、幾何尺寸、面積，各個作業單位間的物流強度見表3、表4。

3.3 布局及優化過程[4]

（1）參數確定。需要確定的參數有理論綜合關聯度rij、種群大小popsize、最大進化代數maxgen、交叉概率pc、變異概率pm。

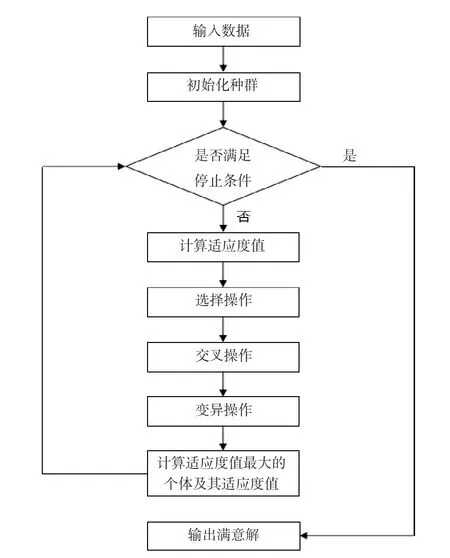
圖3 Matlab求解流程圖

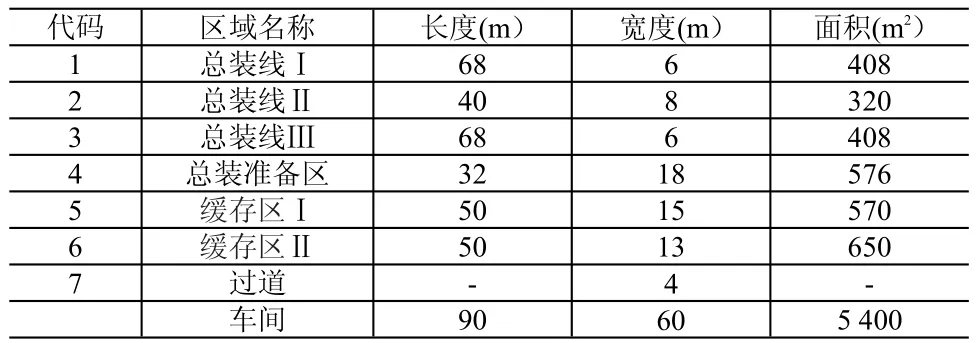
表3 作業單位參數

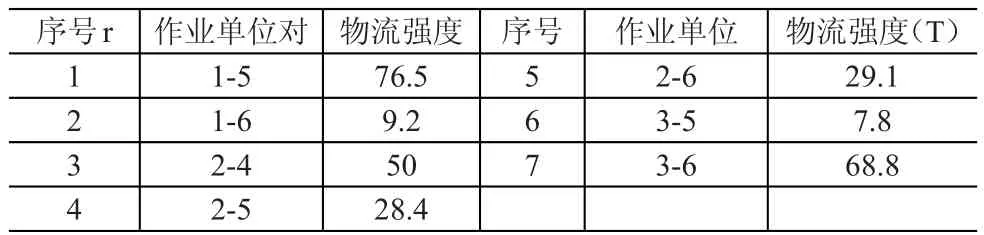
表4 作業單位間的物流強度

①物流分析。將各作業單位對的物流強度按大小排序，根據表4，得到原始物流相關表5。

②非物流分析。首先，界定各作業單位間的關系，包括工藝流程、物流聯系、工作性質形似性等因素；其次，確定各個作業單位之間相互關系的影響因素，評價各個作業單位之間的相互關系等級；最后，得出作業單位非物流相互關系見表6。

③綜合關聯度RIJ。確定物流與非物流相互關系相對重要性，即加權值m:n=1:1；量化物流與非物流相互關系等級；根據表5和表6，綜上分析可得各個工作單位間的綜合關聯度見表7。

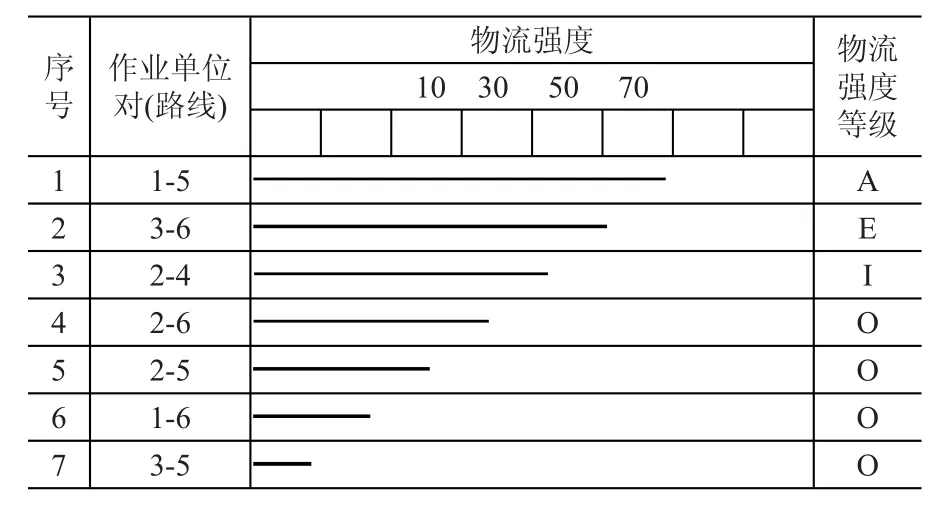
表5 物流強度分析表

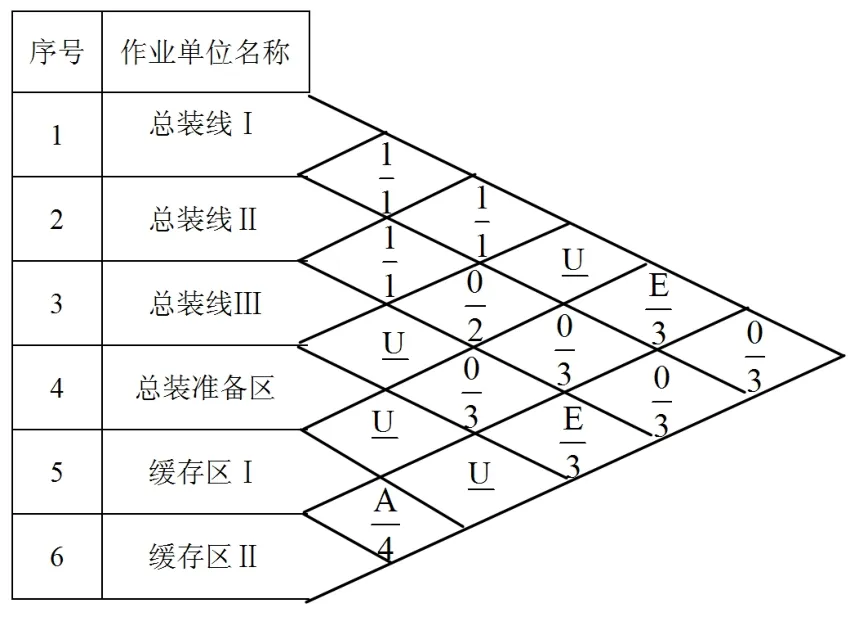
表6 作業單位非物流相互關系表

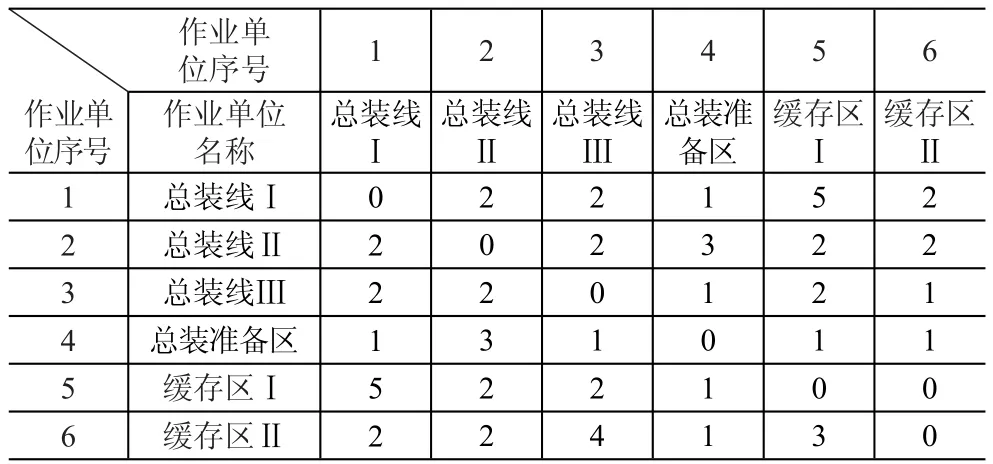
表7 作業單位間的綜合關聯度

（2）其他參數

①種群規模的大小可在[20,100]進行選擇，選擇種群大小popsize=80。

②遺傳算法的最大進化代數[100，500]；取最大進化代數maxgen=200。

③pc一般取為[0.4,0.99]，選取pc=0.9。

④增大pm，增加解空間的多樣性，可得收斂全局最優解；但當變異概率值過大時，會破壞種群中的優良性；pm的取值范圍[0.000 1,0.1]；選取pm=0.1。

綜合上述分析，得遺傳算法的參數如表8所示。

（3）模型求解

①主要變量定義。popsize:種群大小；maxgen：最大進化世代數；lchrom：染色體長度；pc、pm：交叉概率和變異概率；a1、a2：總物流量權重和方差權重；ZL、ZW：整個車間的總長和總寬；L、W：各個工作單位的長度和寬度，表示為矩陣形式；d：走道的寬度；lpopulation,wpopulation：成對的染色體；lpopselect,wpopselect：選擇后的染色體解；lpopcross,wpopcross：交叉后的染色體解；lpopmutate,wpopmutate：變異后的染色體解；fitness：適應度值；currentbest：當前最佳適應度值；bestind：最佳個體；bestfit：最佳個體的適應度；bestever：最佳個體產生世代數。

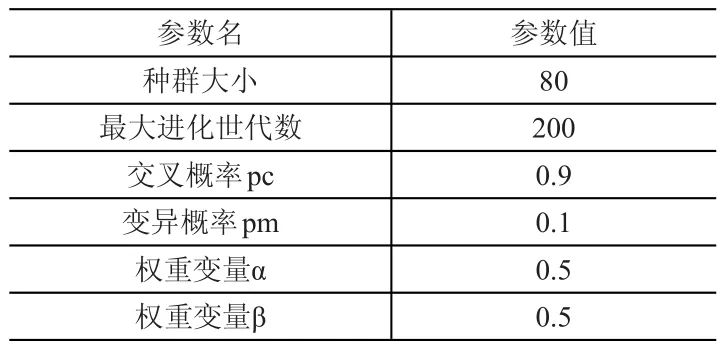
表8 遺傳算法參數表

②功能函數。initpop()：初始化函數；objvalue():計算目標函數值；fitvalue():計算適應度；best():選擇最佳個體；select():選擇操作；cross()：交叉操作；mutate()：變異操作；

③MATLAB中遺傳算法主程序代碼。主程序運行結果見圖4，從圖中得知：生產線U型布局，兩個緩存區5和6鄰近布置，可以大大簡化運輸作業，方便工人多工序操作，節約物流成本。

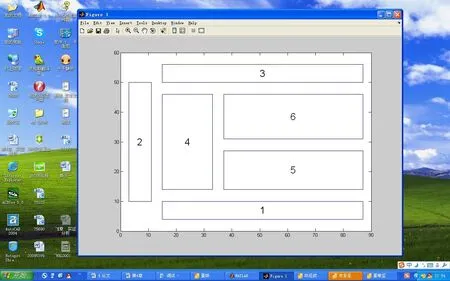
圖4 MATLAB運行結果

4 結論

本文建立了物流緩存區布局的優化模型；應用遺傳算法，并利用MATLAB進行求解，得到物流緩存區優化布局。該方案運行效果顯著，物流緩存區的布局科學合理。

[1]朱耀祥,朱立強.設施規劃與物流[M].北京:機械工業出版社,2003.

[2]王蓀馨.基于遺傳算法的作業車間設備布局優化方法[J].工業工程,2009,12(3).

[3]葉慕靜,周根貴.基于遺傳算法的系統布置設計及初步應用[J].工業工程,2005,(5).

[4]龔全勝,李世其.基于遺傳算法的制造系統設備布局設計[J].計算機工程與應用,2004,(26).