基于浮動車數(shù)據(jù)的城市道路行程時間估計

羅 霞，曹 陽，劉 博，李演洪

?

基于浮動車數(shù)據(jù)的城市道路行程時間估計

羅 霞，曹 陽，劉 博，李演洪

（西南交通大學(xué)，交通運輸與物流學(xué)院，成都 610031）

為提高城市道路行程時間估計模型的準(zhǔn)確度和有效性，本文利用浮動車數(shù)據(jù)，依據(jù)對傳統(tǒng)模型思路的總結(jié)分別建立了基于路段長度比例和點速度調(diào)和平均值的兩種行程時間初階估計模型，并利用統(tǒng)計學(xué)中的同分布融合思想建立了行程時間融合模型，以修正初階模型結(jié)果的精度，彌補傳統(tǒng)估計模型中準(zhǔn)確度低、效率不高的缺陷。最后選取成都市具有代表性的路網(wǎng)區(qū)域為算例，驗證了初階模型假設(shè)分布的正確性，同時計算出融合模型路徑總時間的平均偏差僅為12%，說明了融合模型的準(zhǔn)確度和有效性。

交通工程；行程時間估計；同分布融合；浮動車數(shù)據(jù)

0 引 言

行程時間作為評價道路運行性質(zhì)的關(guān)鍵信息參數(shù)之一，能夠為出行者路徑的選擇及交通部門管理措施的制定提供決策依據(jù)，有助于提高交通流時空分布的合理性。浮動車數(shù)據(jù)憑借其精度高、覆蓋廣、成本低的特點已經(jīng)成為估計行程時間常用的數(shù)據(jù)源之一[1]。目前國內(nèi)外提出的方法主要有兩大類，分別是理論解析法和實際工程模型[2]。

理論解析法主要是利用數(shù)學(xué)理論方法計算道路行程時間。Yang等人利用卡爾曼濾波方法構(gòu)建了行程時間的預(yù)測模型[3,4]，該方法自適應(yīng)性較差，要得到較準(zhǔn)確的結(jié)果需要考慮交通流環(huán)境的影響因素，對輸入?yún)?shù)的類別要求較高；Zheng結(jié)合卡爾曼濾波模型提出了集成的擴展指數(shù)平滑方法[5]；楊立娟同樣利用指數(shù)平滑方法，并融合了神經(jīng)網(wǎng)絡(luò)模型和ARMA（自回歸滑動平均模型）[6]，這兩類方法對數(shù)據(jù)量的要求都較高，數(shù)據(jù)量不夠多時無法得到較準(zhǔn)確的結(jié)果；Hofleitner等人基于貝葉斯方法實現(xiàn)了行程時間的估計[7]；Rahmani利用統(tǒng)計學(xué)方法提出了非參數(shù)估計模型，利用計算得到的平均值作為行程時間結(jié)果[8]。雖然貝葉斯方法和非參數(shù)估計模型可以求得較準(zhǔn)確的路段行程時間結(jié)果，但當(dāng)車輛GPS（Global Positioning System）數(shù)據(jù)量較多時算法的運行效率會顯著降低。

實際工程模型則是將研究重心放在了更微觀的層面，即從單車行程時間分析入手，一般是通過對一定時間內(nèi)特定路段中記錄的瞬時速度進行分析計算獲得行程時間。如武小云利用不同時間間隔內(nèi)的車輛平均速度計算行程時間，最終以行程時間序列標(biāo)準(zhǔn)差離散程度最小為取值標(biāo)準(zhǔn)[9]，這一類方法完全忽略了交叉口延誤，得出的路段行程時間結(jié)果誤差較大。為彌補這一缺陷，充分考慮車輛在交叉口的延誤，一些學(xué)者不再將速度作為主要研究對象，而是利用相鄰數(shù)據(jù)點間記錄的時間、速度以及行駛距離等參數(shù)推斷車輛經(jīng)過路段節(jié)點的時刻，進而通過數(shù)理分析方法得到相應(yīng)的路段行程時間結(jié)果。如王志建總結(jié)了低頻數(shù)據(jù)在交叉口附近相鄰數(shù)據(jù)點的四種分布，并根據(jù)車輛運行特征計算了通過交叉口的時刻[10]，但該方法僅著重分析了車輛在交叉口的延誤，未考慮車輛在非交叉口區(qū)域的速度變化。

為提高行程時間估計精度，本文綜合上述兩類方法思想，提出了一種基于路段長度比例和點速度調(diào)和平均數(shù)的同分布融合模型。模型解決了理論解析法中的算法結(jié)構(gòu)復(fù)雜的問題，效率得到了較大的改善。同時，充分考慮了交叉口延誤和車輛速度變化，準(zhǔn)確度相較于實際工程模型有了明顯的提高。最后，本文還選取成都市部分有代表性的路網(wǎng)進行了行程時間計算，并以一條特定路徑實際行程時間為基準(zhǔn)，對結(jié)果準(zhǔn)確性進行了分析。

1 行程時間初階估計模型

利用地圖匹配方法，可以重建車輛行駛軌跡[11]，得到車輛經(jīng)過的軌跡矩陣和各GPS點對應(yīng)的真實匹配點矩陣，其中包含了軌跡經(jīng)過的所有路段信息，包含了GPS點的實際位置、時間及速度信息。以獲得的信息為基礎(chǔ)，本文提出了兩種行程時間的初階估計模型思路：思路一是依據(jù)路段長度占軌跡總長度的比例制定各路段權(quán)重，進而將路徑時間分配到各路段上；思路二是根據(jù)匹配到各路段上的GPS點記錄的點速度進行路段行程時間估計。這兩類方法各有利弊，第一種考慮了節(jié)點（交叉口）延誤但并不精確，而且沒有分析車輛速度的變化；第二種考慮了車輛速度的變化但是得到的結(jié)果并沒有完全包含節(jié)點延誤時間。基于這兩類方法在一定程度上可以互相補充，本節(jié)先分別利用這兩種模型初步計算路段行程時間，在下一節(jié)中進一步建立融合模型，同時考慮車輛速度的變化和節(jié)點延誤，提高估計結(jié)果的準(zhǔn)確度。另外，由于不同時段交通情況可能會出現(xiàn)較大的改變，如平峰期和高峰期，因此下文建模時僅選擇同一時段的浮動車數(shù)據(jù)。

1.1 基于長度比例的行程時間估計模型

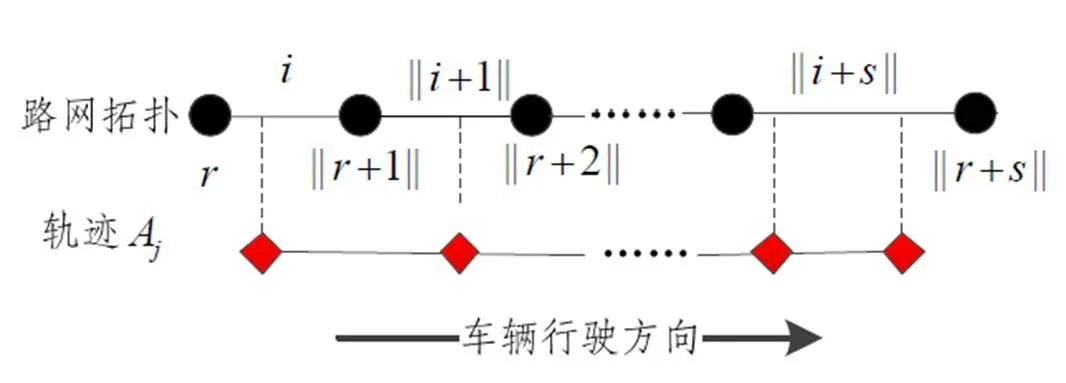
圖1 軌跡匹配示意圖

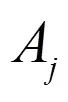
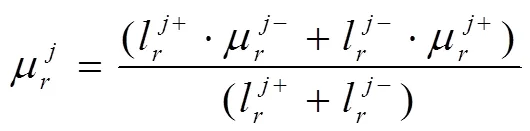
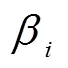
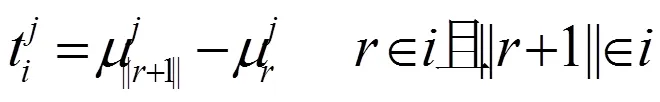
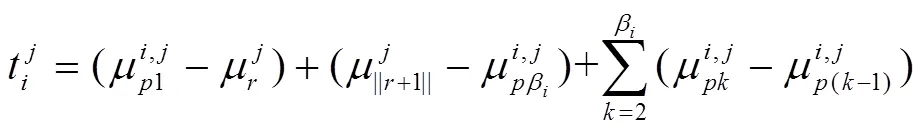
通過模型建立的過程可以發(fā)現(xiàn)，在以路段長度比例為權(quán)重計算節(jié)點時刻時，由于對整條軌跡的行程時間進行了劃分，得出的路段行程時間結(jié)果包含了車輛在節(jié)點處的延誤，但是這一延誤被均勻分配到了路段上，結(jié)果并不能保證完全準(zhǔn)確。同時，該方法沒有考慮車輛的速度變化，默認車輛記錄的GPS點與點之間的速度不變，這對于低頻數(shù)據(jù)來說誤差將變大。

1.2 基于點速度調(diào)和平均值的行程時間估計模型

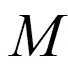
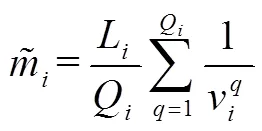
用式（2）計算出來的路徑總行程時間與實際總時間相比往往會存在偏差，如圖2所示。

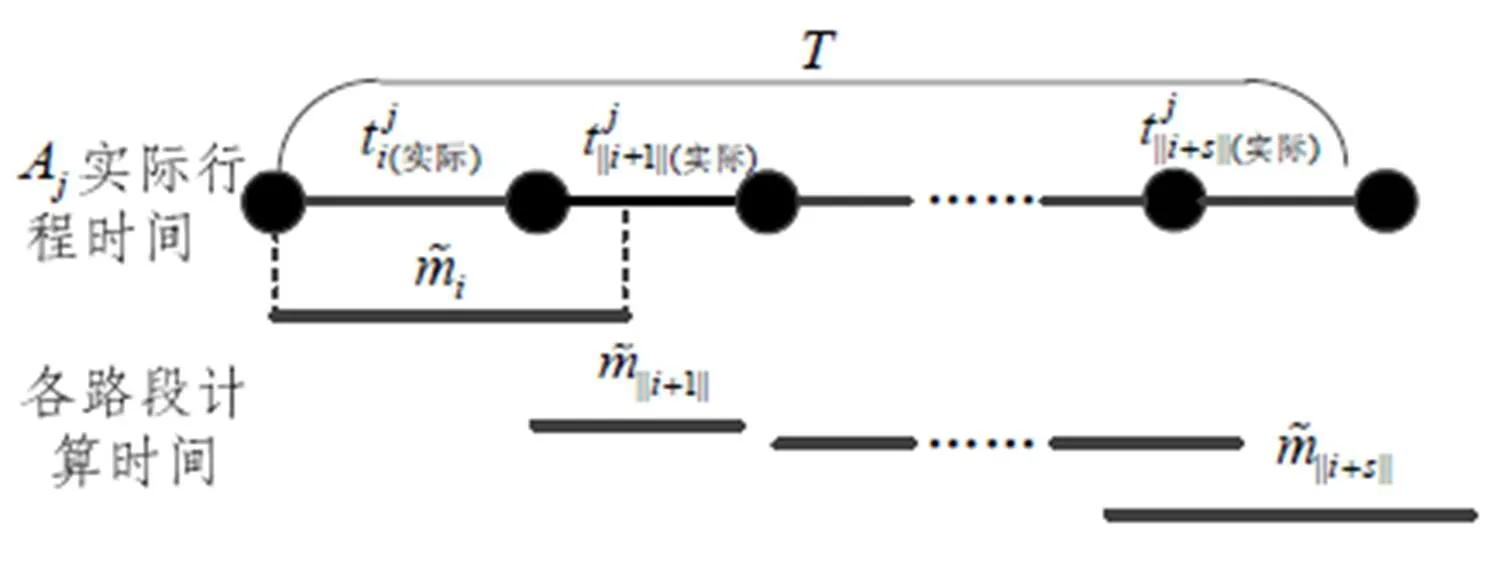
圖2 實際行程時間與計算所得時間偏差示意圖

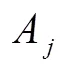
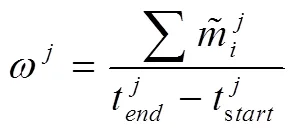
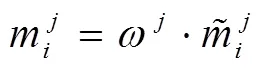
采用上述方法即可得到分布均值和方差。可以發(fā)現(xiàn)，基于點速度調(diào)和平均值來估計行程時間能夠充分體現(xiàn)出車輛在行駛過程中的速度變化，但是車輛的GPS點往往都沒有完全定位到節(jié)點上，對于節(jié)點處的延誤這一方法并不能準(zhǔn)確計算，甚至?xí)耆雎裕虼舜嬖谡`差。

2 同分布融合估計模型

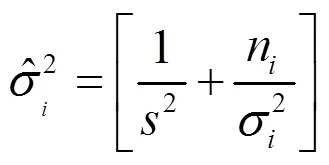
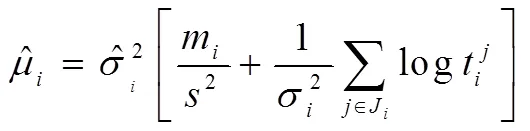
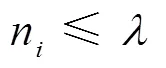
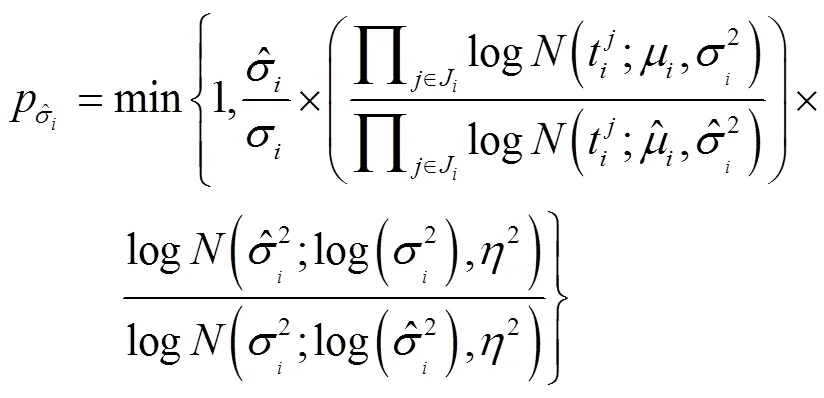
為保證最終結(jié)果的合理性，將拒絕概率的界限值設(shè)為0.7，即，說明原假設(shè)不成立，接受計算出來的路段行程時間分布；否則，說明計算結(jié)果不理想，需按照步長繼續(xù)用M-H方法從剩余樣本量中抽取，直至更新得到拒絕或者該路段的樣本量已全部計算完。為了提高效率以及充分利用樣本，可將取值為2。綜上所述，路段行程時間估計的算法流程如圖3所示。

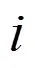
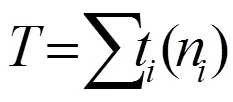
3 算例分析

以成都市2014年11月9日7:30~9:00早高峰時段的浮動車數(shù)據(jù)為例進行計算，該浮動車為出租車，原始數(shù)據(jù)量較大這里不再列出。選取市內(nèi)具有代表性的路網(wǎng)進行算例分析，路網(wǎng)邊界由金房苑路、群星路、九里堤路、一環(huán)路、紅星路等構(gòu)成，其經(jīng)度范圍為104.042 45°~104.101 56°，緯度范圍為30.658 64°~30.710 57°。選取該區(qū)域作為研究對象的原因有兩點：首先，區(qū)域包含學(xué)校和CBD地區(qū)，出行量較大，從而能獲得足夠多的浮動車數(shù)據(jù)量來支撐計算；其次，本研究實驗室位于西南交通大學(xué)，前往CBD地區(qū)的人員和次數(shù)都較多，便于實際行程時間的獲取進而實現(xiàn)模型驗證。選取的路網(wǎng)如圖4所示。

3.1 假設(shè)分布檢驗

以西體北路路段作為示例，來驗證基于長度比例（模型1）和基于點速度（模型2）計算行程時間的結(jié)果是否分別服從所假設(shè)的對數(shù)正態(tài)分布和標(biāo)準(zhǔn)正態(tài)分布。兩種計算結(jié)果均隨機選取40個樣本量，其中基于路段長度比例思路中需要對計算結(jié)果作對數(shù)，再作正態(tài)分布檢驗。通過SPSS軟件的非參數(shù)檢驗中K-S方法進行分析，假設(shè)分布檢驗的結(jié)果如表1和圖5所示。

表1 初階估計模型的假設(shè)分布檢驗參考值

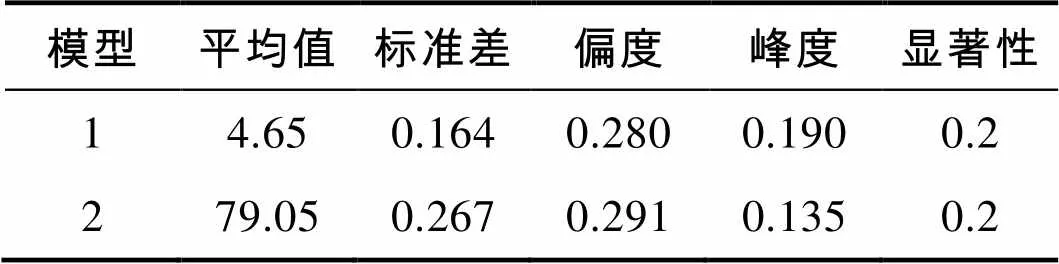
Tab.1 The reference values of the hypothesis distribution test of the initial estimation models

從上表中看出，兩種方法的偏度和峰度值均小于1，且漸進顯著性均大于0.05。同時，從圖5也可近似看出兩種數(shù)據(jù)類型服從正態(tài)分布，因此證明了這兩種思路的原假設(shè)是成立的。

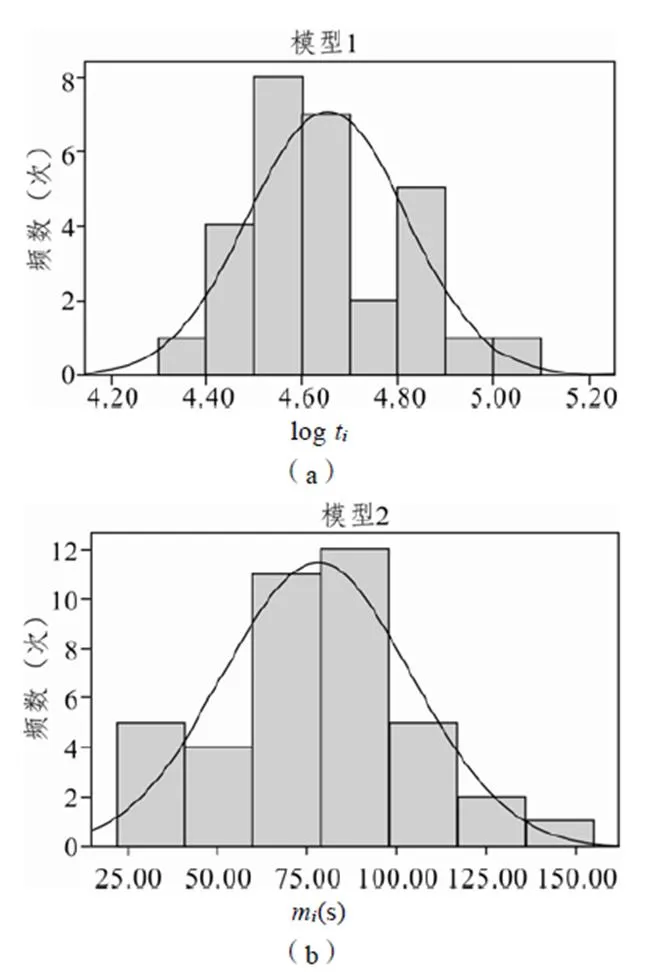
圖5 兩種思路的假設(shè)分布檢驗

3.2 結(jié)果對比分析

進一步對兩種初階模型進行融合，進而得到路網(wǎng)中各路段最終的行程時間結(jié)果，如圖4所示。為驗證結(jié)果合理性，以西南交通大學(xué)北門至天府廣場為例進行分析驗證，見圖4加粗顯示路徑。以7:30~9:00坐出租車的實際出行時間為參照，連續(xù)試驗3天，并將這3天的數(shù)據(jù)進行平均作為最終所得數(shù)據(jù)，判斷該路徑上的上述幾種思路的效果以及融合方法所計算路段行駛時間的準(zhǔn)確程度。

以所選的路徑為例，將初階估計模型和同分布融合模型的結(jié)果與實際路段的行程時間結(jié)果進行對比，如表2所示。根據(jù)結(jié)果進一步分析偏差，得到如圖6所示的偏差對比圖。

表2 三種行程時間估計結(jié)果對比

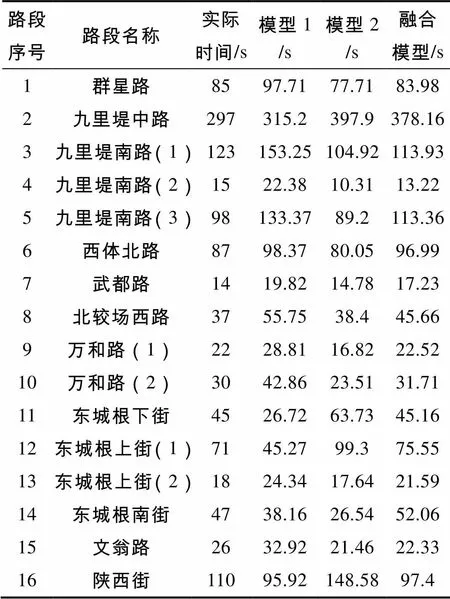
Tab.2 The comparison of estimation results of the three times

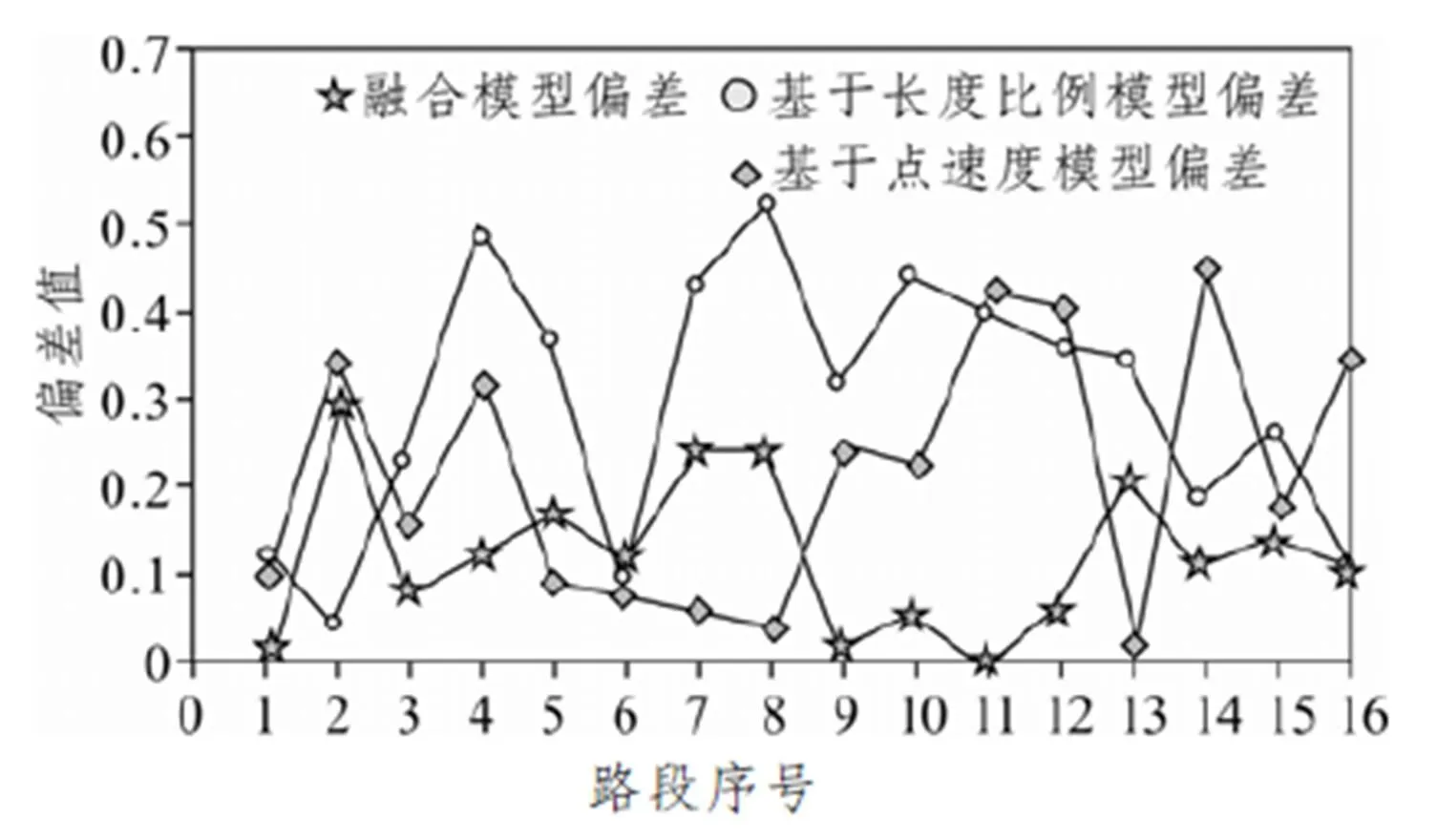
圖6 三種模型偏差結(jié)果

從圖6中可以發(fā)現(xiàn)，基于長度比例和基于點速度的模型所得結(jié)果偏差波動較大，并且偏差在30%以上的結(jié)果較多，有的甚至高達40%以上，因此可以說明初階模型估計的結(jié)果并不準(zhǔn)確。而融合后的模型偏差值大大降低，并且比較穩(wěn)定，只有少數(shù)路段偏差大于20%，說明融合后路段行程時間估計值的準(zhǔn)確度有了大幅提升。其中發(fā)現(xiàn)偏差較大的有路段行程時間過長的九里堤北路和過短的武都路，九里堤北路是擁堵較為常發(fā)的路段，其車輛行程時間變化幅度較大；而武都路，并不是由于變化量大，而是由于本身基數(shù)較小的原因?qū)е碌摹Ａ硗猓捎趯崪y數(shù)據(jù)的時間與所采用的GPS數(shù)據(jù)日期不同，交通條件在不斷變化，也是誤差的來源之一。

對三種模型計算平均偏差，可以發(fā)現(xiàn)基于長度比例的行程時間估計方法偏差最高，平均值達30%，而基于點速度的行程時間估計方法偏差次之，平均值達21%。這是因為后者不僅以速度區(qū)別各路段，在計算的過程中也考慮了路段長度，并由路徑總行程時間作了總量控制。而融合方法的平均偏差為12%，相對較低。綜合以上分析，與前初步估計模型的計算結(jié)果比較，融合方法的計算結(jié)果偏差更小，路段行程時間更為精準(zhǔn)。若采用的GPS浮動車數(shù)據(jù)的規(guī)模更大，其他軟硬件設(shè)施更加完備的情況下，相信所獲取的結(jié)果將更貼合實際的路網(wǎng)情況。

4 結(jié)束語

本文對傳統(tǒng)的實際工程模型加以改進，提出了利用路段長度比例和點速度調(diào)和平均數(shù)初步估計路段行程時間的方法，并在這一基礎(chǔ)上，結(jié)合統(tǒng)計學(xué)思想，對初步估計模型的結(jié)果加以融合，得到更加準(zhǔn)確的城市道路行程時間。與傳統(tǒng)方法相比，不僅提高了結(jié)果的精確度，還降低了算法的復(fù)雜程度，使得估計過程更加易于實現(xiàn)。通過分析實際算例結(jié)果，可以發(fā)現(xiàn)行程時間估計模型得出的各路段時間值與真實值存在一定的偏差，但大部分在可接受的范圍內(nèi)，整條路徑的行程時間偏差較小，因此說明本文提出的時間估計模型具備有效性。

由于基于路段長度比例和基于點速度的兩種模型對于交叉口延誤的計算都不完全準(zhǔn)確，因此融合后的算法在這一方面仍考慮得不夠完善，如何合理有效地估計交叉口延誤需要在下一階段研究中進一步深入探討。

[1] SHALABY A S, ABDULHAI B, BYON Y J. GISTT: GPS-GIS integrated system for travel time surveys[D]. England: University of Toronto, 2006.

[2] 李慧兵, 楊曉光, 羅莉華. 路段行程時間估計的浮動車數(shù)據(jù)挖掘方法[J]. 交通運輸工程學(xué)報, 2014, 14(6): 100-116.

[3] YANG J S. Travel time prediction using the GPS test vehicle and Kalman filtering techniques[C]// American Control Conference, Portland: IEEE, 2005: 2128-2133.

[4] HAGE R M, BETAILLE D, PEYRET F, et al. Unscented Kalman filter for urban network travel time estimation[J]. Procedia-Social and Behavioral Sciences, 2012, 54(2290): 1047-1057.

[5] ZHENG F, WAN Y, WU P. Link travel-time prediction using extended exponential Smoothing and Kalman filter in dynamic networks[C]// Eighth International Conference of Chinese Logistics and Transportation Professionals. Chengdu: ASCE, 2009: 3753-3759

[6] 楊立娟. 基于浮動車的城市道路行程時間采集與預(yù)測方法研究[D]. 長春: 吉林大學(xué), 2007.

[7] HOFLEITNER A, HERRING R, ABBEEL P, et al. Learning the dynamics of arterial traffic from probe data using a dynamic bayesian network[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1679-1693.

[8] RAHMANI M, JENELIUS E, KOUTSOPOULOS H N. Non-parametric estimation of route travel time distributions from low-frequency floating car data[J]. Transportation Research Part C Emerging Technologies, 2015, 58: 343-362.

[9] 武小云. 基于GPS浮動車的城市交通路段行程時間實時估算方法研究[D]. 廣州: 華南理工大學(xué), 2010.

[10] 王志建, 馬超鋒, 李梁. 低頻GPS數(shù)據(jù)和交叉口延誤下的行程時間估計[J]. 西南交通大學(xué)學(xué)報, 2015, 50(2): 361-367.

[11] CHANDIO A A, TZIRITAS N, ZHANG F, et al. An approach for map-matching strategy of GPS-trajectories based on the locality of road networks[J]. Lecture Notes in Computer Science, 2015, 9502(1): 234-246.

[12] 漸猛. 基于浮動車的道路交通狀態(tài)判別方法研究[D]. 淄博: 山東理工大學(xué), 2013.

（中文編輯：李愈）（英文審改：胡路）

Travel Time Estimation for Urban Roads Based on Floating Car Data

LUO Xia，CAO Yang，LIU Bo，LI Yan-hong

（School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China）

To improve the accuracy of the model for estimating travel time of urban roads, based on we develop two kinds of initial estimation models of travel time based on the length ratio of the road and the mean value of the point velocity respectively. The two models employ the floating car data and the traditional model idea. Then a travel time fusion model is developed based on the same-distribution fusion ideas in statistics, which corrects the accuracy of the initial estimation models. This also improves the accuracy and efficiency of the tradition models. Finally, a representative road network area in Chengdu is selected as an example. The correctness of the hypothetical distribution of the initial estimation models are verified and the average deviation of the total path time of the fusion model is calculated to be only 12% , demonstrating the accuracy and validity of the fusion model.

traffic engineering; travel time estimation; same-distribution fusion; floating car data

1672-4747（2018）02-0001-08

U491.1

A

10.3969/j.issn.1672-4747.2018.02.001

2017-04-07

成都市科技項目（2015-RK00-00208-ZF）

羅霞（1962—），女，四川樂至人，西南交通大學(xué)交通運輸與物流學(xué)院教授，研究方向為智能交通。

羅霞，曹陽，劉博，等. 基于浮動車數(shù)據(jù)的城市道路行程時間估計[J]. 交通運輸工程與信息學(xué)報, 2018, 16(2): 1-8.