典型跟馳模型的特征與性能分析*

陳 征 閆冬梅 劉 釗 郭建華

(1.南京理工大學自動化學院 南京 210094; 2.東南大學智能運輸系統研究中心 南京 210018)

車輛跟馳(Car Following，CF)模型主要研究前車行駛過程中狀態改變所引起的后車相應的變化行為，通過車輛逐一跟馳的方式描述單一車道上的交通流特性，建立駕駛員微觀行為與交通流宏觀現象之間的聯系。在過去60多年的發展過程中，學者們相繼提出了許多不同形式的跟馳模型，取得了豐富的研究成果[1]。車輛跟馳模型在微觀交通仿真、交通安全評價和通行能力分析等領域得到了廣泛應用。因此，對跟馳模型進行充分研究，從而揭示交通流運行的內在機理，完善微觀仿真系統，提高交通仿真的現實性，具有重要的理論價值和現實意義。本文首先闡述跟馳模型的發展背景，然后分析典型模型GM模型、Gipps模型和全速度差模型的基本形式、假設條件和基本特性。最后，通過實例研究，對比分析不同跟馳模型下車輛跟馳過程中的位置、速度和加速度等參數的變化，分析車輛行駛狀態的變化。

1 跟馳模型的發展背景

跟馳模型的研究始于20世紀50年代。1953年，Pipes[2]提出車輛跟馳模型，但該模型忽視了車頭間距對跟馳行為的作用。這時期的車輛跟馳理論適用于無超車的單車道密集交通狀態。Chandler等[3]給出GM(general motors，GM)模型的原始模型，通過對實驗結果的分析，發現加速度與車頭時距不顯著相關，而與相對速度顯著相關。Gazis等[4]給出GM模型的常規表達式，并通過調整模型參數取值，得到不同的流量-密度關系表達式。

1959年，Kometani等[5]提出安全距離跟馳模型，該模型在前車與后車速度的基礎上計算安全的跟馳距離。Gipps[6]考慮了車輛的安全距離和加速度約束，提出一個新的安全距離模型，該模型假設跟隨車能在引導車突然制動后安全停下來。之后，Helbing和Tilch[7]提出類似于分子動力學的廣義力(general force，GF)模型，該模型克服了Bando等[8]提出的優化速度模型(optimal velocity model，OVM)中的加速度過高、未考慮駕駛員反應延遲時間與車輛停止處易發生碰撞等問題，但當前車的速度與后車相比足夠快時，雖然前后兩車間的距離比安全間距小，后車駕駛員仍不會減速，GF模型不能對該現象進行解釋。因此，何民等[9]建立考慮相對速度的車輛跟馳模型，并分析該模型的穩定性。在此之后，相關學者提出了考慮前后車輛間的速度差為正負時對車輛加速度影響的全速度差(full velocity difference，FVD)模型[10-12]。

隨著元胞自動機(cellular automata，CA)理論的發展，Cremer等[13]將元胞自動機理論引入交通流模型構建中。Wolfram[14]基于元胞自動機理論，提出非常簡單的184號模型。184號模型將路段分為等長度的格點，每個格點視為1個元胞，最多能容納1輛車，若某一時刻格點無車，其左側格點有車，則在下一時刻，左側格點的車輛向前行駛占據該格點；若某一時刻格點有車，其右側格點也有車，則該格點的車輛就會因為沒有行駛空間而停止不動。在184號模型研究基礎上，Nagel等[15]考慮最大速度和隨機慢化率2個重要參數，建立著名的Nasch模型，首次將基于個體行為學習的CA模型應用于交通仿真過程。元胞自動機模型將交通流理論引領到新領域，拓展了車輛跟馳行為建模的研究范圍。

2 典型跟馳模型

2.1 刺激-反應模型

Gazis等認為車輛跟馳理論的中心思想是每個駕駛員對特定的刺激做出反應，并將其總結為關系式：反應=靈敏度×刺激，其中刺激可以是車輛位置和它們對時間的導數的函數，也可以是其他參數，反應取為車輛的加速度。GM模型是典型的刺激-反應模型，基本表達式為：

(1)

GM模型是大多數跟馳模型研究的基礎，該模型結構簡單，物理意義明確，清楚地反映出車輛跟馳行駛的制約性、延遲性和傳遞性。GM模型雖然屬于微觀模型，但它建立了微觀駕駛行為與宏觀交通流之間的聯系。另外，GM模型也具有局限性，實際運行中跟馳行為受交通和流量等條件的影響，而模型中只考慮了前車刺激對后車反應的作用；模型依據的試驗數據都是在低速條件下獲取的，不能反映普遍的跟馳行為；跟隨車對正負相對速度的反應程度相同，而實際觀測表明相對速度正負不同時，跟隨車的反應是不一致的。

2.2 安全距離模型

為了分析道路網絡條件變化對交通流的影響，提出了安全距離類模型。Gipps模型屬于安全距離類模型(collision avoidance model，CAM)，即尋找一個特定的跟馳距離，當前車行為改變，前后車之間的距離小于該特定跟馳距離時，就有可能發生碰撞。Gipps[6]假設跟隨車能在引導車突然制動后安全地停下來，考慮駕駛員和車輛的速度、加速度、位置限制：

(0.025+vn)(t)/Vn1/2

(2)

(3)

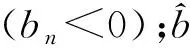
Gipps模型降低了模型參數標定時參數范圍選擇的難度，提高了模型參數標定的精度。此外，Gipps模型考慮了反應時間，避免仿真過程中反應時間與仿真不一致而引起的各種問題。然而，在車輛行駛過程中，Gipps模型要求所有車輛必須恰好行駛在當前車輛行駛狀態決定的安全距離上，這與現實中車輛的行駛情況不符。

2.3 優化速度模型

考慮到行駛的車輛都有不同的行駛速度，而該速度又取決于與前車之間的距離，Bando等提出了優化速度(optimal velocity model，OVM)模型，該類模型能展現宏觀交通流中時走時停、突發的交通阻塞和激波等現象。考慮前車車速大于后車車速的情況，提出了全速度差(full velocity difference model，FVD)模型，則：

(4)

式中：κ為靈敏度常數；λ為Δv的權系數隨模型應用條件變化；V(s)為優化速度函數。

FVD模型同時考慮了速度差為正負時對跟馳車的影響，更符合實際的交通阻塞密度與車輛延誤時間。FVD模型在車輛行駛過程中不會產生過高的加速度，此外，它能描述交通流的相變和交通擁堵的形成等實際的交通現象。但當前后車的速度相等或差別很小且車頭時距也很小時，假設由于突發事故或交叉口紅燈使前車突然制動，并產生較大制動加速度，在FVD模型中易發生前后車碰撞的情況。

3 實例分析

以GM模型、Gipps模型和FVD模型為實例，計算車輛跟馳中行駛狀態的變化。在計算過程中，僅考慮由2輛車組成隊列中的跟馳狀態，并且假設車輛都以勻加速或勻減速狀態行駛。

3.1 模型建立

對GM模型，主要根據Edie[16]的研究結果，選擇假設條件中參數m和l的取值。對Gipps模型，主要是依據Gipps的研究成果。對FVD模型，選擇了常用的優化速度函數。同時，由于GM模型、Gipps模型和FVD模型是根據不同的車輛跟馳原理而建立起來的，因此模型仿真的基本初始參數的選擇也不盡相同。這3個模型的具體假設條件和初始參數的設置見表1。

表1 模型主要假設條件及初始參數信息

3.2 結果比較

根據設置的模型假設條件和初始參數值，GM模型、Gippes模型和FVD模型的數值仿真結果見圖1～3，包括車輛的速度變化和位置變化情況。

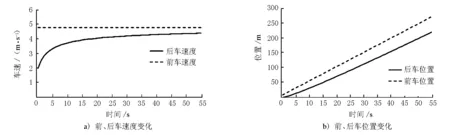
圖1 GM模型計算結果

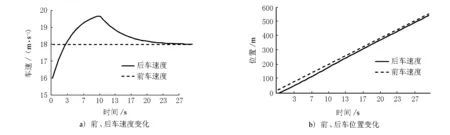
圖2 Gipps模型計算結果

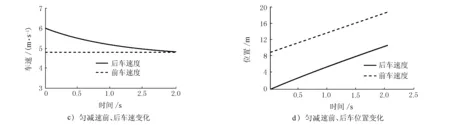
圖3 FVD模型計算結果

由圖1a)可見，GM模型的前后車速度變化情況為：當前后車速度差較大時，后車的加速度較大；當后車速度逐漸接近于前車速度時，后車的加速度逐漸減小為零，前車和后車的速度差保持穩定。在圖1b)中，前后車跟馳過程中車間距離逐漸增大。由圖2a)可見，在Gipps模型中，后車的速度迅速增加，在超過前車速度之后逐漸減少，最終與前車速度相同。這是由于在Gipps模型中，后車的速度在滿足期望速度限制后受限于安全距離，因此后車的速度減少，并趨于穩定。此外，由圖2b)可見，Gipps模型中，前后車之間的距離逐漸減小，逐漸接近車輛的有效長度。對于FVD模型而言，分為勻加速和勻減速2種情況。其中，圖3a)和b)為勻加速情況，圖3c)和d)為勻減速情況。由圖3a)和b)可見，當后車的速度小于前車的速度時，后車的速度逐漸增加，并與前車速度一致，同時前后車之間的車距基本保持不變，這是因為后車根據前后車相對位置及最優速度改變其速度。而在圖3c)和d)中，當前車的速度小于后車的速度時，后車的速度逐漸減小，與前車車速一致，同時前后車之間的車距基本保持不變。

總的來說，由圖1～3可見，在保證前后車正常行駛的條件下，GM模型、Gipps模型和FVD模型展現出了不同的特性。GM模型是較早提出的微觀跟馳模型，僅考慮駕駛員的刺激反應，其模型建模簡單，只能反應理想條件下單一因素下車輛跟馳情況。在此基礎之上，考慮車輛之間的距離因素，發展出了Gipps模型，該模型較能體現車輛跟馳過程中速度控制的影響。而FVD模型的發展更符合實際情況，能夠較為準確地描述單一車輛加速或減速的行駛特性。

4 結語

本文通過具有代表性的跟馳模型，GM模型、Gipps模型和FVD模型，對比分析了刺激-反應類模型、安全距離類模型和優化速度類模型的特性。以具體的數值仿真為例，對比分析GM模型、Gipps模型和FVD模型中車輛速度和車輛位置變化的特點。結果表明，GM模型考慮的跟馳影響因素較為單一，只能適用于理想條件下的跟馳過程，Gipps模型能夠較好地體現出行駛速度因素在跟馳過程中的影響，而相較于前2種模型，FVD模型則能夠更好地適用于實際跟馳情況。

[1] 孫俊，商蕾，高孝洪.交通仿真模型及其應用研究[J].交通科技，2004(4)：102-104.

[2] PIPES L A.An operational analysis of traffic dynamics[J].Journal of Applied Physics,1953,24(3):274-281.

[3] CHANDLER R E,HERMAN R,MONTROLL E W.Traffic dynamics: studies in car following[J].Operations Research,1958(2):165-184.

[4] GAZIS D C,HERMAN R,ROTHERY R W.N-onlinear follow-the-leader models of traffic flow[J].Operations Research,1961(4):545-567.

[5] KOMETANI E,SASAKI T.Dynamic behavior of traffic with a nonlinear spacing-speed relationship[C]// Elsevier. Proceeding of the Symposium on theory of Traffic Flow.New York:Elsevier,1959:105-119.

[6] GIPPS P G.A behavioural car-following model for computer simulation[J].Transportation Research Part B: Methodological,1981,15(2):105-111.

[7] HELBING D,TILCH B.Generalized force model of traffic dynamics[J].Physical Review E,1998,58(1):133.

[8] BANDO M,HASEBE K,NAKAYAMA A, SUGIYAMA Y.Dynamical model of traffic congestion and numerical simulation[J].Physical Review E,1995,51(2):1035-1042.

[9] 何民，榮建，任福田.判定跟馳狀態的研究[J].公路交通科技，2001，18(4)：74-78.

[10] 姜銳,吳清松.交通流復雜動態特性的微觀和宏觀模式研究[J].中國科學院研究生院學報，2006(6)：848-854.

[11] 支梁,史忠科,劉通.一種交叉路口全速度差改進模型[J].交通運輸系統工程與信息,2013,13(6):80-85.

[12] 王建都, 張俊樂.一種改進全速度差模型的穩定性分析與仿真[J].計算機工程與應用,2016,52(7):24-27.

[13] CREMER M,LUDWIG J.A fast simulation model for traffic flow on the basis of boolean operations[J].Mathematics & Computers in Simulation,1986,28(4):297-303.

[14] Wolfram S.A new kind of science[M].Champaign: Wolfram Media,2002.

[15] NAGEL K,SCHRECKENBERG M.A cellular automaton model for freeway traffic[J].Journal de physique I,1992,(12):2221-2229.

[16] EDIE L C.Car-following and steady-state theory for noncongested traffic[J].Operations Research,1961,9(1):66-76.