基于神經網絡的光柵信號軟件細分技術的研究

湯 攀，張厚武，何 勇

(貴州大學 計算機科學與技術學院，貴州 貴陽 550025)

1 概 述

光柵位移傳感器是精密的光柵測量系統,適用于大量程的精密測量，并在醫療設備、儀器制造、機械生產、武器研制等方面起著重要作用[1]。隨著精密加工技術與超精密加工技術的發展，對測量精度的要求越來越高，而常用的50線/毫米經濟型的光柵傳感器，它的精度為20 μm，難以達到精密測量的要求。因此需要對光柵傳感器輸出的信號進行細分來提高測量的精度。

朱維娜等[2]提出了一種基于DSP的光柵細分技術，以DSP為主芯片，實現對25線光柵尺不低于10倍細分計數；胡曉東等[3]提出運用FPGA為主芯片，既提高了解位移算法的正確性，也提高了運算速度；李懷瓊等[4]提出了一種采用數字信號處理與軟件計算的細分方法，實現莫爾條紋八細分；王冠雅等[5]提出對采集到的信號進行分析時,使用軟件細分的方法,實現了光柵信號的80倍細分。但是以上的細分方法都是基于硬件實現的，實現起來復雜，并且很難對其進行擴展。

目前主流的細分技術主要有：四細分、電阻鏈移相細分、鎖相倍頻細分、幅值分割細分、神經網絡細分[6-7]。將以上五種細分方法從細分倍數、優點、缺點以及應用方面進行分析對比，選擇出適合的細分方法。對比分析如表1所示。

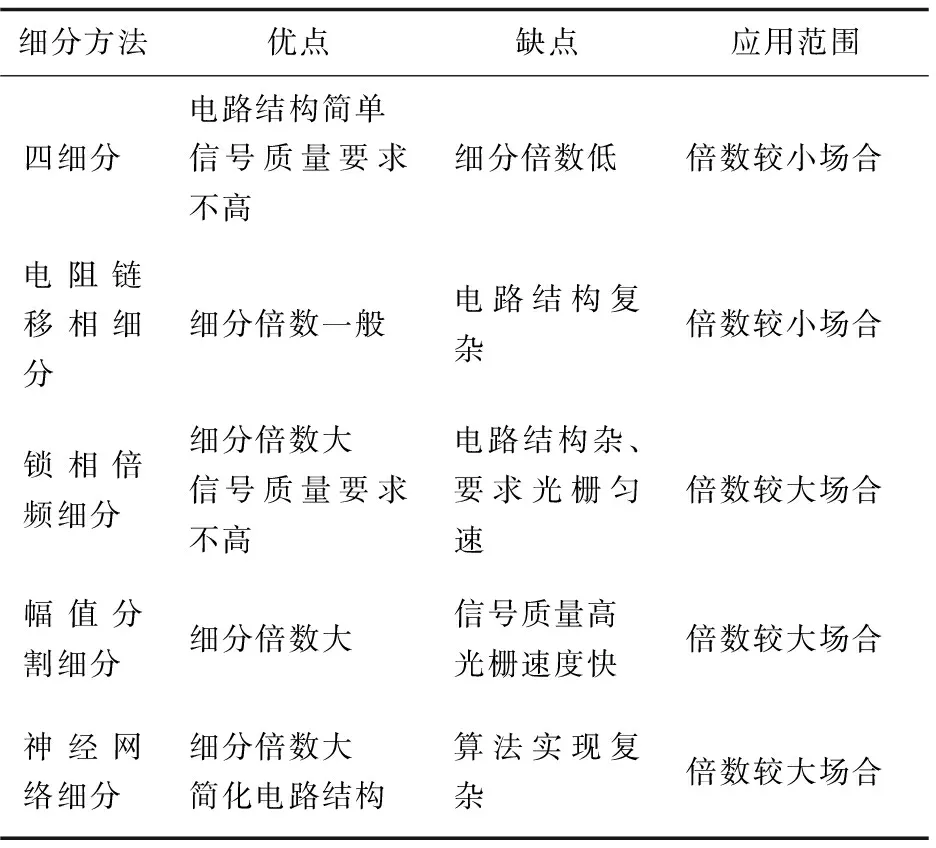
表1 光柵信號細分方法的對比分析

2 細分原理

2.1 測量系統總體設計

光柵傳感器輸出的四路相位相差90°的正弦信號送至差動放大電路，既可以消除偶次諧波的影響，也能消除直流電平帶來的誤差，然后得到兩路相位相差90°的正弦信號，再送至整形電路將原始光柵信號轉換成方波信號，將方波信號送入FPGA進行四細分、辨向和可逆計數，完成大數計數的功能，單片機讀取FPGA計數器的值，并運用串口COM6傳給后臺；與此同時，送至AD模塊進行AD采樣，然后傳給串口COM7，后臺直接讀取串口COM7的AD值，送入神經網絡細分程序完成小數細分。最后結合大數值和小數值計算出總位移量。

2.2 細分原理

選用50線/mm的經濟型光柵尺，光柵尺移動一條刻線相當于光柵信號移動一個周期(一個周期的正弦信號)，即移動了20 μm。通過FPGA將整形后得到與光柵信號周期一致的方波信號進行計數，即可求得所測的大數值，實現硬件四細分。設不足1/4個周期的位移值表示為d，則具體位移可表示為：

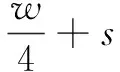
(1)

其中，k為大數計數值；s為不足1/4周期的微位移值；w為光柵的柵距。

為了獲得精位移值s，需對不足1/4個周期的小數部分進行高倍細分。只能運用光柵輸出的正余弦信號才能進行高倍細分。由于光柵傳感器輸出的正余弦信號幅值較小，若直接運用細分效果不佳，故需先對光柵輸出的四路相位相差900的正弦信號進行放大處理，得到近似正弦和余弦信號：

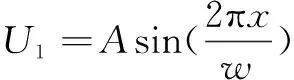
(2)

(3)

從公式中可以看出，電信號和光柵位移存在一定的函數關系，即光柵傳感器移動的位移x可通過測量的電壓U值計算得出。精細分就是運用光柵信號的電壓幅值與位移值之間的數學關系，通過對信號進行A/D采樣轉換，再運用查表或者數學關系式計算出微位移[8]。文中的精細分是運用神經網絡算法實現的。由于正、余弦信號線性度不好，特別是在峰值附近時，只有光柵尺的位移變化量較大才能產生一個微小的電壓變化，如果直接將采集的正余弦信號作為網絡輸入，則從細分原理上會帶來很大誤差。設計用式4作為輸入量：

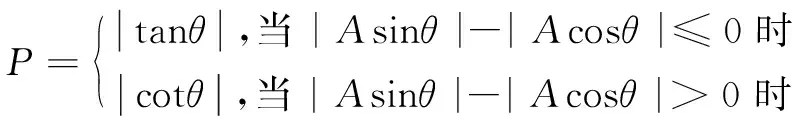
(4)

根據以上分段函數圖像的對稱性，|Asinθ|-|Acosθ|>0時的微位移值仍可用(0，π/4]訓練的模型得出，故只需對(0，π/4]區間內的樣本進行訓練，得到網絡模型。具體關系如表2所示，其中x表示神經網絡的直接輸出量。

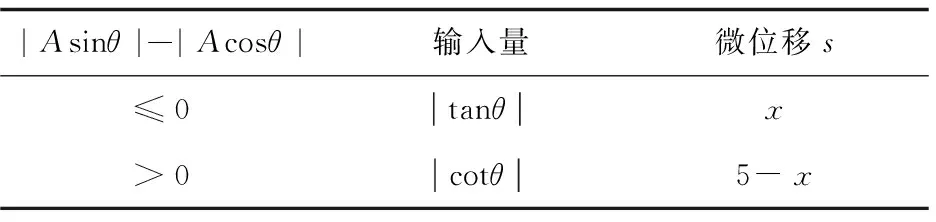
表2 Asinθ|-|Acosθ|、網絡輸入、輸出量的關系

3 BP神經網絡結構和算法設計

3.1 BP神經網絡

郭雨梅等[9]提出只有一個隱層的三層神經網絡,只要隱節點足夠多，就可以以任意精度逼近一個非線性函數。故文中選取三層BP神經網絡對光柵信號進行精細分。當然隱層節點數并不是越多越好，根據實驗誤差最小，選取最合適的隱層節點數。

3.2 樣本點選取及學習過程

為了消除幅值不穩定性帶來的影響，選取[P,S]作為訓練樣本的輸入,P為上一節介紹的分段函數。實際的樣本數據由精度較高的光柵位移系統測出。光柵傳感器輸出的兩路互補正弦信號經A/D轉換后，判斷|Asinθ|-|Acosθ|的正負，確定網絡的輸入量,再送入神經網絡子程序，經過神經網絡程序，得出對應1/4周期內的微位移量。每1/4周期對應的區間依次為(0°,90°)、(90°,180°)、(180°,270°)、(270°,360°)，根據分段函數P的對稱性，可將(0°,90°)、(90°,180°)、(180°,270°)、(270°,360°)四個區間通過區間(0°,45°)的神經網絡模型進行計算。根據系統要求，可確定采用一個輸入一個輸出的神經網絡模型。第1層為輸入層；第2層為隱含層，傳遞函數選取S型“tansig”;第3層為輸出層，傳遞函數選取“purelin”[10-12]。BP神經網絡訓練過程復雜，耗時時間長，故文中設計將樣本數據在MATLAB中運用neff函數創建一個名為net的BP神經網絡模型，并運用train函數進行訓練，得出各層的權值和閾值。將這些權值和閾值作為初始值存入寄存器，然后再編寫神經網絡細分子程序進行運算，得出最終細分結果。在編寫神經網絡子程序時需要用到以下公式：

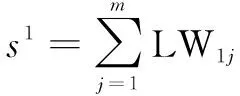
(5)

(6)

y=f(s2)

(7)

其中，LW1j、bj、IWj1、oj分別為輸入層到中間層的權值、中間層各神經元閾值、中間層到輸出層的權值、輸出層各神經元閾值。

隱含層的傳遞函數為S型激活函數，輸出層的傳遞函數為線性函數，故得到式8：

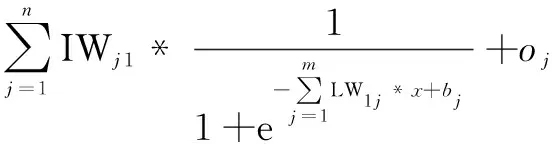
(8)

BP神經網絡的隱含層節點數，根據經驗可以參照以下公式進行設計。

(9)

其中，h為隱含層節點數；a為輸入節點數；b為輸出節點數；c為1～10之間的調節常數。由此可知隱含層節點數范圍為[2,12]。

不同節點數的網絡訓練誤差如表3所示。

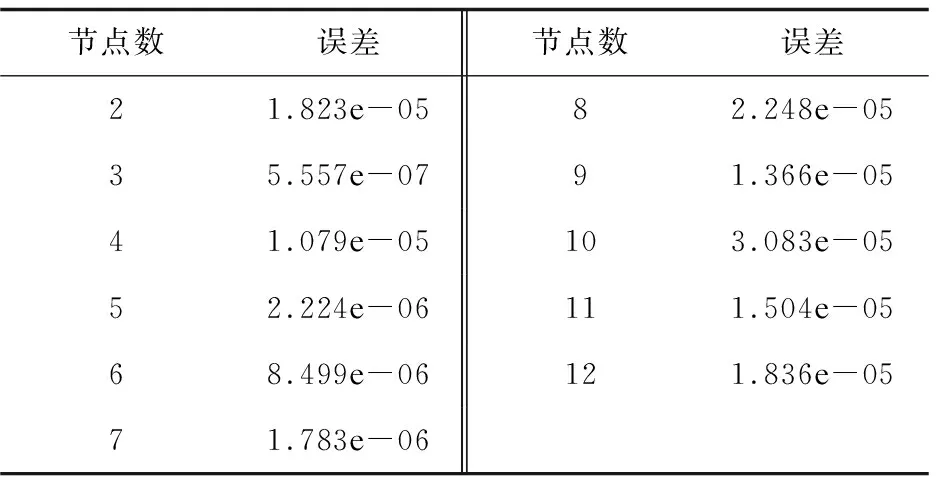
表3 不同節點數的網絡訓練誤差

從表3可以看出，隱含層節點數越多，網絡性能并非越好。當隱含層節點數從9增加到12時，誤差反而增大。而隱含層節點數為3時誤差最小。故選用一個隱層節點數為3的三層網絡模型。

4 改進的BP神經網絡算法設計

由于BP神經網絡算法本身的原因，學習過程可能收斂于局部極小點。而遺傳算法是一種自適應全局優化概率搜索算法[13-16]。該算法從很多點開始并行工作，不是局限于一點，故能有效防止搜索過程收斂于局部最優解。前面介紹了網絡結構最優的設計，在此基礎上，再運用遺傳算法的全局搜索能力，搜索到最優的網絡權值和閾值。遺傳算法主要包括染色體編碼與解碼，個體適應度的檢測評估，選擇，交叉，變異等。遺傳算法可描述為：

(1)確定種群的大小N為40，交叉概率設為0.7，變異概率設為0.01；根據網絡結構，產生N個(LW,IW),通過二進制編碼，將(LW,IW)中每一個權值轉換成二進制編碼，然后組合構成一個完整的染色體。產生N個權值的取值范圍為[-20,20],閾值的取值范圍為[-10,10]的染色體，將得到由N個染色體構成的初始群體C。

(2)計算出每個個體的適應度fi,再按賭輪盤法進行優質個體的選擇，產生新種群。

(3)根據算術交叉方式以及確定的交叉概率，把部分基因進行交換，形成新個體。

(4)通過基因中的某一位變異，可以防止種群陷入超平面，根據設置的變異概率進行變異操作。

(5)重復步驟2～4，直到誤差對連續幾代種群趨于穩定或不超過某一閾值，則進化計算結束。經過上述方法優化，獲得一個接近最優的權值和閾值，再運用BP算法再次尋優，采用梯度下降法，得到網絡最優解。

5 硬件設計

該系統硬件主要包括差分放大電路、整形電路、粗細分模塊和AD模塊。FPGA主要實現四細分、辨向、計數以及神經網絡子程序、綜合數據處理等功能。

5.1 FPGA選型

文中選用ALTERA公司的Cyclone IV系列芯片，型號為EP4CE6F17C8，是256腳的FBGA封裝。這款FPGA可以利用其擴展口直接連接到ADDA模塊、攝像頭、4.3寸液晶屏、音頻模塊等等，使用起來極其方便。

5.2 粗細分模塊

光柵每移動一個柵距輸出一個正弦波。粗細分就是將這一個正弦波分為4段，即四細分。四細分主要是通過辨向與計數的原理來實現的。光柵尺輸出的信號，經過前端模擬電路的處理，將得到兩路互補的方波信號進行計數，這兩路方波信號分別經過兩個D觸發器，第一個觸發器D與第二個觸發器D延時一個時鐘周期。電平狀態按照0010-1011-1101-0100順序循環變化時，進行加計數操作，即光柵尺正向運動;電平狀態按照0001-0111-1110-1000順序循環變化時，進行減計數操作，即光柵尺反向運動。

5.3 放大器的設計

光柵輸出的正弦信號有漂移值，而漂移值會影響精度的提高，故文中設計用兩個四運放LM324N對光柵信號進行處理。

5.4 A/D轉換模塊設計

光柵輸出信號經過預處理電路處理(由于篇幅有限，不再詳細介紹)，得到兩路互補正弦信號U1和U2。AD模塊部分采用了兩片ADI公司的AD9226將模擬信號轉換成12 bit的數字信號，文中運用兩片AD芯片能同時對以上兩路信號進行處理，減小了AD轉換需等待的誤差。經過預處理電路后的信號電壓變化在-5～5 V之間，而AD9226芯片其電壓輸入范圍為1.0～3.0 V，故文中運用衰減電路來實現上述要求，轉換公式為：Vout=1/5Vin+2。AD922的數據轉換速率最高為65 MHz，光柵尺的截止頻率f=v/w,文中選用的光柵尺速度v不超過120 m/min,柵距為0.02 mm。假設信號周期為100 kHz,根據采樣定理，采樣頻率至少大于200 kHz,實驗中采樣頻率設置為50 MHz,滿足設計要求。經過AD轉換后得到數字信號，以給FPGA處理。AD采樣模塊程序運用Verilog HDL語言實現。

5.5 通訊模塊設計

將光柵尺最終測得的位移值通過串口通信發送給PC端。硬件設計采用Silicon Labs CP2102GM芯片作為USB和UART電平轉換的橋梁,USB接口采用Micro USB接口。引腳RXD接FPGA的M2腳，引腳TXD接FPGA的N1腳，引腳RXD是從PC發送給FPGA的串行數據,引腳TXD是從FPGA發送給PC的串行數據。通訊主要采取串行數據傳輸方式，消息幀主要由起始位、數據位、校驗位等組成。串口發送程序包含3個程序：時鐘產生程序clkdiv.v、串口發送程序uarttx.v和串口發送測試程序。這三個程序都是用Verilog HDL語言建模實現的。

6 軟件設計

細分系統的硬件設計完成后，還需對其進行軟件設計。在Quartus II開發環境下，運用Verilog HDL語言編程。光柵信號經過一系列的硬件電路處理后，由FPGA完成四細分并對AD模塊進行采樣，通過兩個串口分別將計數器的值和采集的值傳給上位機，然后由上位機讀取串口的數據，判斷細分方法的選擇，最后得出相應細分方法測得的位移值。FPGA和上位機的軟件流程分別如圖1和圖2所示。

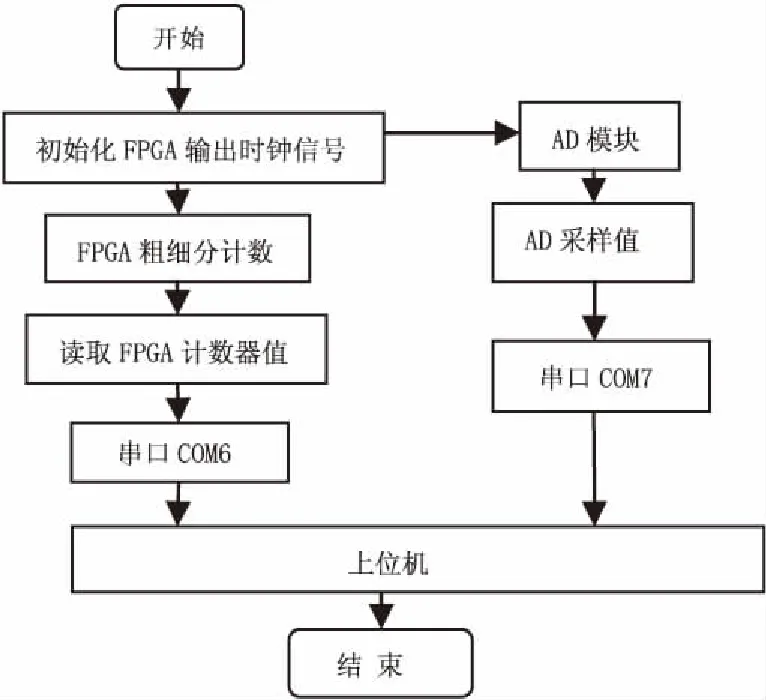
圖1 FPGA軟件程序流程

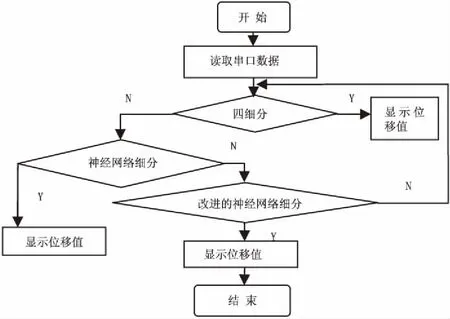
圖2 上位機軟件程序流程

7 實驗結果分析

根據上述細分方案，編寫上位機測控軟件，采集非樣本點的數據進行位移理論計算，實驗數據如表4所示。從表中可以看出，實際位移值和理論值的絕對誤差遠小于10-2數量級范圍，滿足系統要求。改進后的神經網絡細分算法測量值的絕對誤差比未改進的測量值的絕對誤差小，說明改進算法提高了光柵測量的精度，驗證了文中細分算法的可行性，提高了系統的穩定性和細分倍數。

表4 理論值與實際值對比

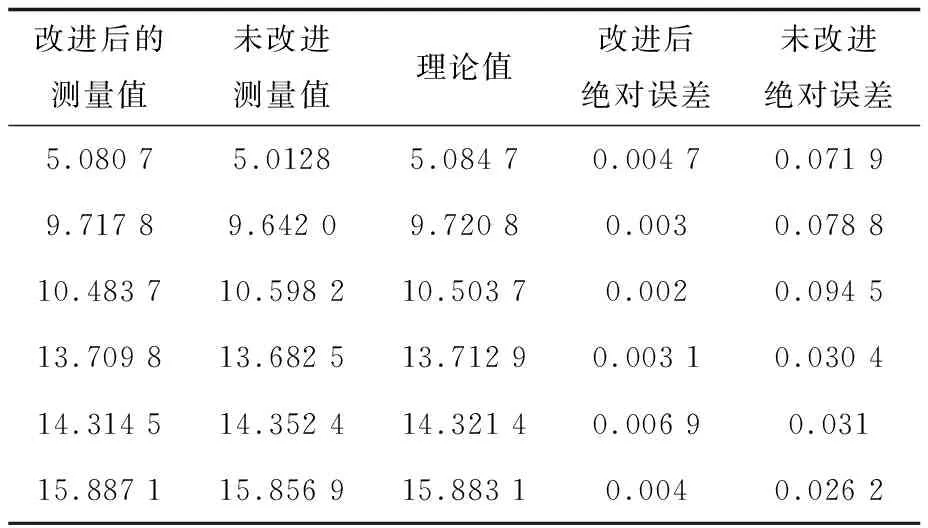
μm

8 結束語

文中詳細論述了如何運用軟硬件相結合的細分方法(硬件細分采用四細分，軟件細分采用BP神經網絡細分)來提高光柵的細分倍數，并對神經網絡算法進行了改進。通過采集非樣本點數據進行測試，驗證了該細分方法的可行性，并可簡化硬件結構,提高系統的可靠性和抗干擾能力,具有一定的實用價值。該神經網絡軟件細分技術具有一定的創新性，同時也對硬件實現神經網絡細分算法較復雜的問題提供了新的解決途徑，但目前只是初步完成了提高細分倍數的目的，還未對光柵測量系統進行優化。未來的研究重點是對其誤差進行自動補償。

參考文獻：

[1] 李金艷.基于幅值采樣技術的光柵信號細分的研究[D].哈爾濱：哈爾濱理工大學,2013.

[2] 朱維娜.基于DSP2812的光柵細分技術研究[D].成都:西南交通大學，2012.

[3] 胡曉東.基于FPGA與單片機的高精度電子經緯儀光電信號處理系統研制[D].南京：南京理工大學，2004.

[4] 李懷瓊,陳 錢,王 鈺.新型光柵信號數字細分技術及其誤差分析[J].計量學報,2001,22(4)：281-283.

[5] 張金杰.鑒相法光柵位移測量系統的研究[D].沈陽:沈陽工業大學,2008.

[6] 于 耕，馬曉梅，郭華鵬．圓光柵測角系統信號細分電路設計[J]．電子設計工程，2012,20(15):99-102.

[7] 金建新．輸出正交正弦波的光柵尺在位移測量中的脈沖細分原理[J]．自動化儀表,2002,23(1):17-19.

[8] SANCHEZ-BREA L M,MORLANES T.Metrological errors in optical encoders[J].Measurement Science and Technology,2008,19(11):115104.

[9] 郭雨梅,關 蕊,鐘 媛.基于徑向基神經網絡的光柵細分方法[J].沈陽工業大學學報，2011,33(2):193-197．

[10] 丁 旭,李彬華,楊曉晗.一種基于FPGA的光柵信號細分方法[J].傳感技術學報,2016,29(6):846-853.

[11] HU Haijiang, ZHANG Fengdeng. Advanced bidirectional subdivision algorithm for orthogonal fringes in precision optical measurement instruments[J].International Journal for Light and Electron Optics,2012,123(15):1322-1325．

[12] 關 蕊.基于神經網絡的莫爾條紋信號細分方法與應用[D].沈陽:沈陽工業大學,2010.

[13] 雷英杰，張善文，李續武,等.遺傳算法工具箱及應用[M].西安：西安電子科技大學出版社，2005.

[14] SUN Q,CHE W G,WANG H L.Bayesian regularization BP neural network model for the stock price prediction[M]//Foundations and applications of intelligent systems.Berlin:Springer,2014:521-531.

[15] GURESEN E,KAYAKUTLU G,DAIM T U.Using artificial neural network models in stock market index prediction[J].Expert Systems with Applications,2011,38(8):10389-10397.

[16] ROVITHAKIS G A,CHALKIADAKIS I,ZERVAKIS M E.High-order neural network structure selection for function approximation applications using genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,2004,34(1):150-158.