K均值聚類算法的研究與優化
陶 瑩,楊 鋒,劉 洋,戴 兵
(廣西大學 計算機與電子信息學院,廣西 南寧 530004)
0 引 言
數據挖掘在實際應用中的主要任務之一是聚類分析,其是數據挖掘中一個很熱門的研究領域,同時與其他學科的研究方向有很大的交叉性[1]。聚類分析可以發現數據隱含的結構,對數據進行自動歸類,從而得到數據的大致分布,在諸多領域為決策提供支持信息[2]。
K均值聚類算法是聚類分析方法中一種基本的劃分式方法[3]。由于該算法簡便易懂,且計算速度較快,通常被作為大樣本聚類分析的首選算法[4]。
但是一般的K均值聚類算法初始聚類中心的選擇是隨機的,這樣會導致聚類結果的不穩定。而且算法中k的值需要人為提前設定,k值設定的合理與否會直接影響聚類的效果[5]。此外,噪聲和離群點也會對聚類效果產生影響,使得聚類中心偏離主要數據區域[6]。因此,文中針對K均值聚類算法的隨機性較強的特點進行改進。
1 K均值聚類算法
1.1 算法基本思想
首先在整個數據集中任意選擇k個數據作為初始聚類中心,然后計算其他數據對象與k個聚類中心的距離,將數據對象劃分到距離最近的聚類中心所在的聚類域。所有數據劃分好后,重新計算k個聚類中每個聚類的全部數據對象的平均值,該平均值所在的數據點成為新的聚類中心。最后進行多次迭代,直到連續兩次的聚類中心相同,說明此時數據對象類別劃分完畢,即得到k個聚類[7]。
1.2 算法評價準則—誤差平方和
評價聚類效果,可以定義一個數據對象和其所在聚類域的目標函數。通過目標函數的取值情況評價聚類效果[8]。常用的聚類算法評價準則是中心誤差的平方和,即:
(1)
其中,Xu是數據u的全部屬性值所構成的矢量;k是聚類個數;m1,m2,…,mk是k個聚類中心對應的矢量;cj是聚類中心為mj的聚類域。
聚類中心矢量mj表示為:
(2)
其中,Nj為聚類域cj中數據的個數。
式1中,目標函數J代表k個聚類里的全部數據與其聚類中心mj之間的誤差平方和,值越小表明聚類中數據的集中性越好,即得到的聚類效果越好[9]。
1.3 算法局限性分析
(1)K均值聚類算法中的k值(待聚類簇的個數)必須由用戶輸入。
k值必須是用戶最先確定,即分為多少個聚類。但是在一些實際情況下,合適的聚類數目k用戶也是未知的,在這種情況下,就需要運用其他辦法來獲得到聚類的數目[10]。
(2)k個聚類中心的選擇是隨機的。
一般K均值聚類算法初始中心是隨機選擇的,然后進行聚類和迭代,并最終收斂達到局部最優結果[11]。因此,聚類結果對于初始中心有著嚴重的依賴,隨機選擇初始中心會造成聚類結果有很大的隨機性。
(3)K均值聚類算法對于噪聲和離群點數據非常敏感。
K均值聚類算法中每個聚類的中心都由每個聚類里所有數據求均值得到。當有與其他數據不一致的數據或者差異比較大的數據時,計算出的聚類的中心易受干擾,偏離主要數據區域,影響聚類效果。因此,K均值聚類算法對數據中的噪聲和離群點非常敏感[12-13]。
2 全局K均值聚類算法
2.1 算法基本思想
全局K均值聚類算法從k=1的聚類開始,即先求出所有數據的聚類中心m。當k=2時,將聚類中心m作為其中一個初始聚類中心,然后依次將數據集的每個點作為另一個聚類的初始中心,即運行n次K均值聚類算法,計算誤差平方和J后,取值最小的點確定為第二個聚類中心,其中聚類后得到了新的聚類中心m1,m2。如果k=3,4,…,n,以此類推[14]。
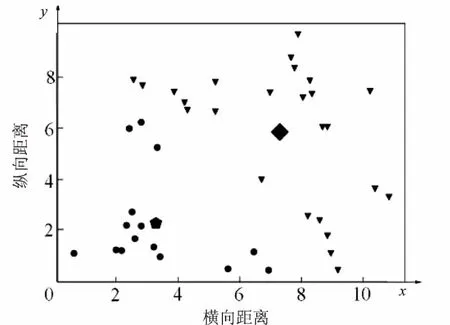
全局K均值聚類算法最終得到了所有k(k 當k=2時,對40個數據重復使用K均值聚類算法得到4種不同的結果,如表1和圖1~4所示。根據誤差平方和評價準則,最好的實驗結果是實驗一,其誤差平方和是112.92386462,但K均值聚類算法本身的不穩定性使得每次產生不一樣的聚類結果,不一定是最優的,甚至是很差的聚類結果。 表1 K均值聚類算法4次實驗結果 圖1 K均值聚類結果一 圖2 K均值聚類結果二 圖3 K均值聚類結5三 圖4 K均值聚類結果四 下面使用改進的K均值聚類算法即全局K均值聚類算法對數據進行實驗。當k=1時,得到聚類中心m=[-0.20740458,0.0553751],再用m分別和每一數據點為中心進行K均值聚類算法。實驗數據見表2。 表2 全局K均值聚類算法實驗數據 全局K均值聚類的結果如圖5所示。 圖5 全局K均值算法聚類結果 與K均值聚類算法相比,全局K均值聚類算法的誤差平方和J=112.923113,改善了K均值聚類算法的隨機性所導致不理想結果的可能性。全局K均值聚類算法不受初始聚類中心位置的影響,并且通過一種確定有效的方法能夠最小化誤差平方和。 聚類算法發展到今天,已經衍生出了多種算法。其中,經典的K均值算法作為劃分聚類算法中最基礎的算法,由于其高效性和簡單性被廣泛應用于各領域[16]。然而,K均值算法也有其固有的局限性,而很多針對K均值算法的改進都極大地降低了算法本身的性能,這顯然是得不償失的[17]。對此,文中對K均值聚類算法進行了改進,降低了算法的不穩定性,提高了聚類的有效性。 參考文獻: [1] 周 濤,陸惠玲.數據挖掘中聚類算法研究進展[J].計算機工程與應用,2012,48(12):100-111. [2] 盤俊良,石躍祥,李娉婷.一種新的粒子群優化聚類方法[J].計算機工程與應用,2012,48(8):179-181. [3] ABDEYAZDAN M.Data clustering based on hybrid K-harmonic means and modifier imperialist competitive algorithm[J].Journal of Supercomputing,2014,68(2):574-598. [4] HUNG C H,CHIOU H M,YANG Weining,et al.Candidate groups search for K-harmonic means data clustering[J].Applied Mathematical Modelling,2013,37(24):10123-10128. [5] 丁祥武,郭 濤,王 梅,等.一種大規模分類數據聚類算法及其并行實現[J].計算機研究與發展,2016,53(5):1063-1071. [6] 萬 靜,張 義,何云斌,等.基于KD-樹和K-means動態聚類方法研究[J].計算機應用研究,2015,32(12):3590-3595. [7] 羅軍鋒,鎖志海.一種基于密度的k-means聚類算法[J].微電子學與計算機,2014,31(10):28-31. [8] 王 濤,卿 鵬,魏 迪,等.基于聚類分析的進程拓撲映射優化[J].計算機學報,2015,38(5):1044-1055. [9] SAHOO A K,ZUO M J,TIWARI M K,et al.A data clustering algorithm for stratified data partitioning in artificial neural network[J].Expert Systems with Applications,2012,39(8):7004-7014. [10] 賈洪杰,丁世飛,史忠植.求解大規模譜聚類的近似加權核k-means算法[J].軟件學報,2015,26(11):2836-2846. [11] 朱建宇.K均值算法研究及其應用[D].大連:大連理工大學,2013. [12] GüNG?R E,?ZMEN A.Distance and density based clustering algorithm using Gaussian kernel[J].Expert Systems with Applications,2017,69:10-20. [13] 趙 麗.全局K-均值聚類算法研究與改進[D].西安:西安電子科技大學,2013. [14] 雷小鋒,謝昆青,林 帆,等.一種基于K-Means局部最優性的高效聚類算法[J].軟件學報,2008,19(7):1683-1692. [15] 張建萍.基于計算智能技術的聚類分析研究與應用[D].濟南:山東師范大學,2014. [16] AHMAD A,HASHMI S.K-harmonic means type clustering algorithm for mixed datasets[J].Applied Soft Computing,2016,48:39-49. [17] TU Chunhao,JIAO Shuo,KOH W Y,et al.Comparison of clustering algorithms on generalized propensity score in observational studies:a simulation study[J].Journal of Statistical Computation and Simulation,2013,83(12):2206-2218.2.2 實驗數據分析

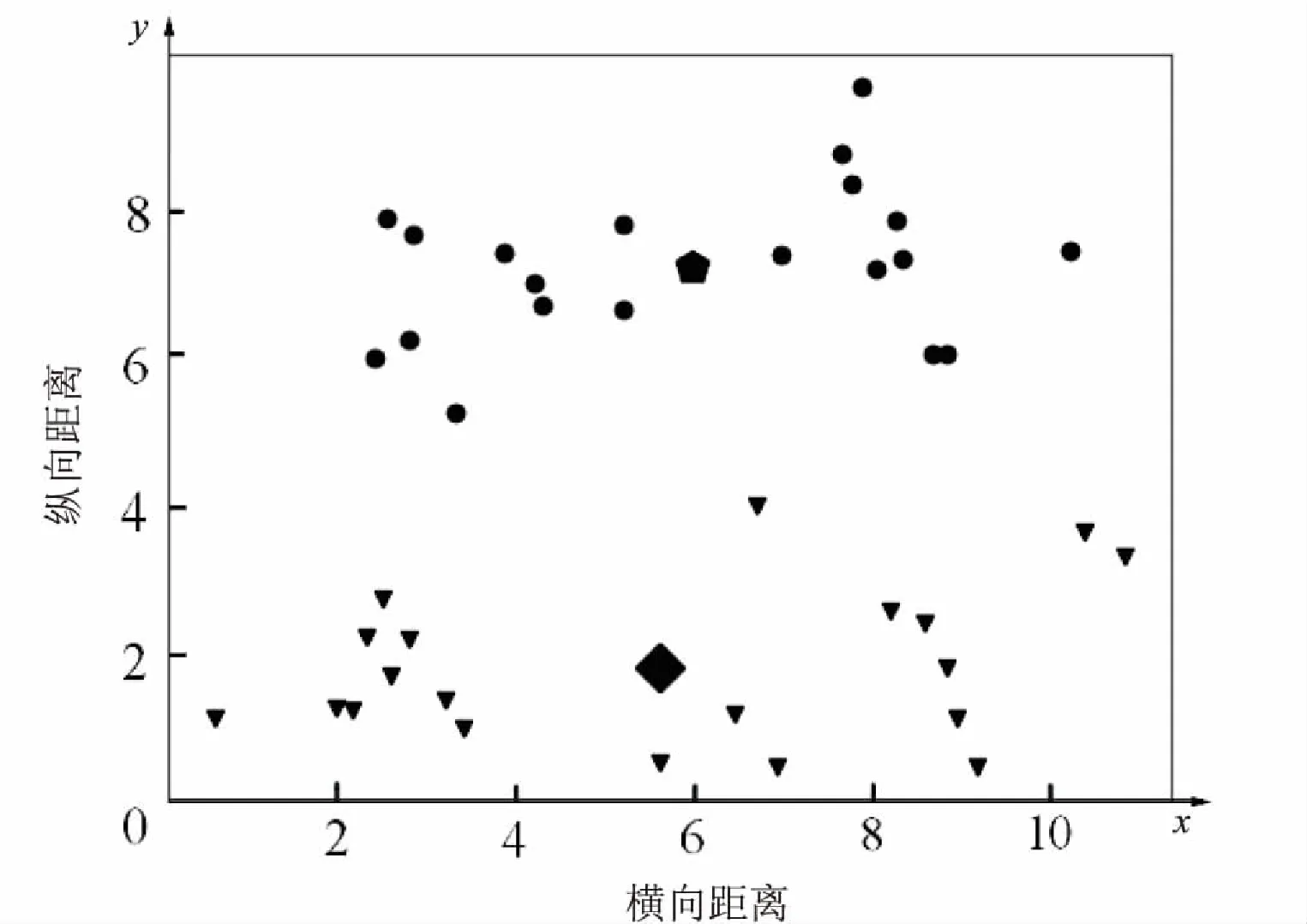
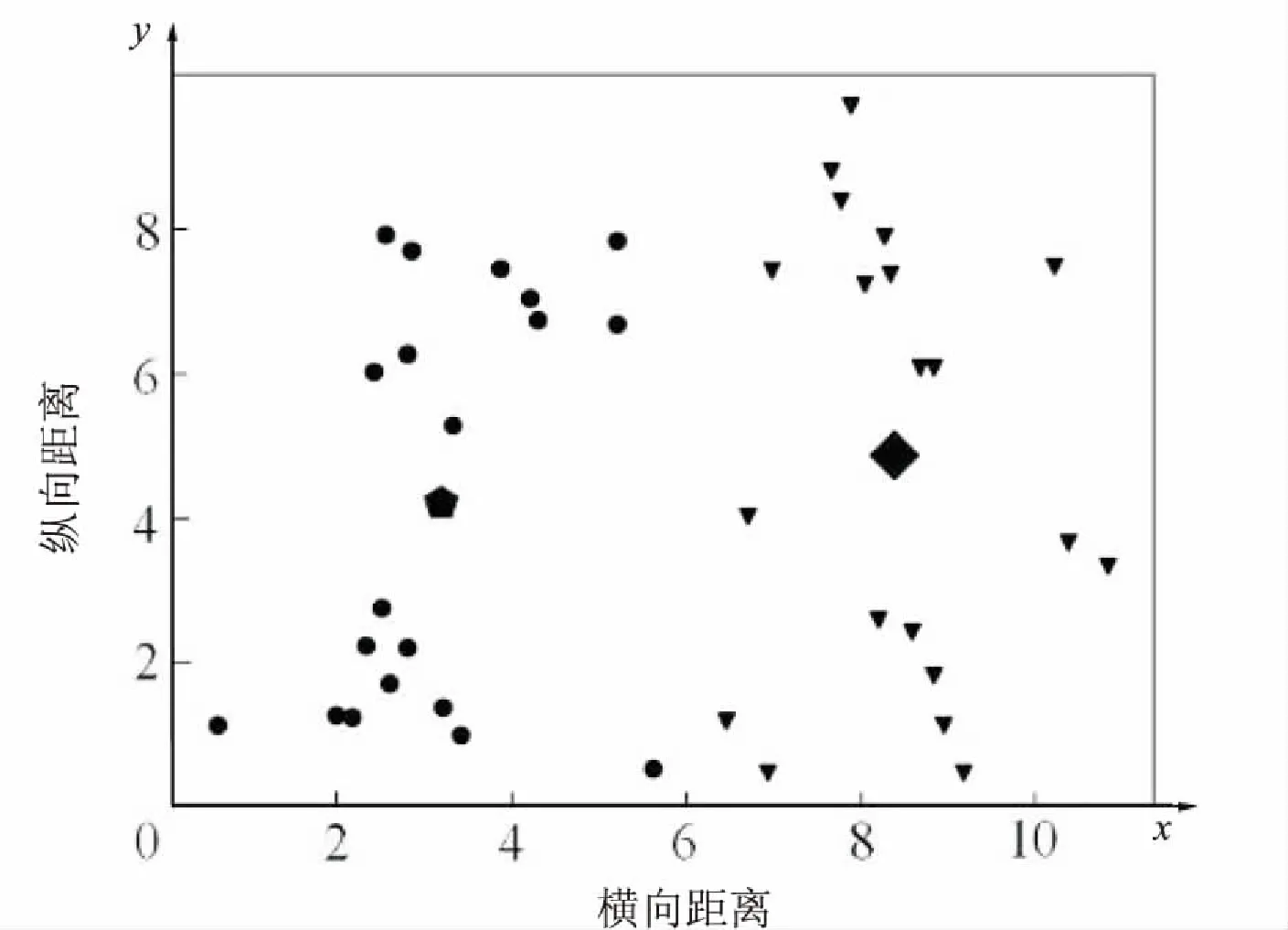

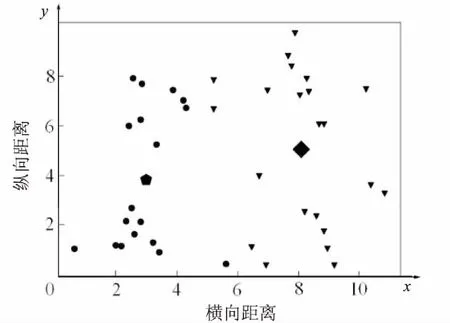
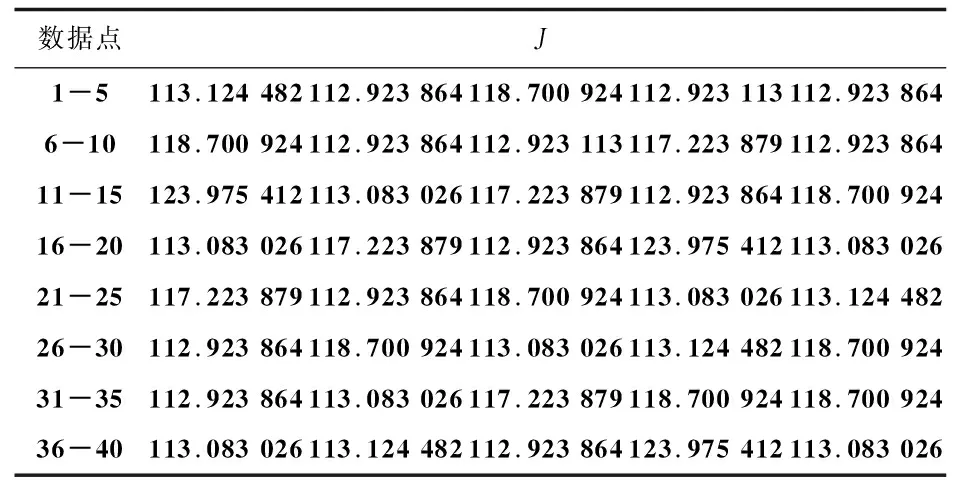
3 結束語

