考慮振動頻率及振幅變化影響的橋梁斷面氣動特征分析
楊青 曹曙陽


摘要: 為探究不同振動頻率、振幅對橋梁斷面氣動特性的影響,利用可在靜止網格中計算動邊界繞流問題的浸入邊界算法,編寫出數值計算程序,展開豎向正弦強迫振動橋梁斷面的繞流模擬,其振幅變化范圍A=0.14D~0.25D,振動頻率變化范圍Stc=0.1~0.25。研究發現:不同振幅下的橋梁斷面阻力系數均在靜止渦脫頻率處產生峰值,橋梁斷面升力系數則在此處均出現歸零效應,且振幅越大,歸零效應愈明顯;迎風面下翼緣可能是決定橋梁斷面阻力系數和升力系數隨振動頻率變化的關鍵因素,橋梁結構在不同振動頻率處呈現不同的渦量分布,但是在同一振動頻率處僅改變物體運動振幅,斷面流場渦量分布基本保持不變;振動頻率是決定表面脈動壓力分布的重要因素,振幅只會改變其值的大小,不影響其脈動壓力分布特性。
關鍵詞: 橋梁斷面; 風致振動; 浸入邊界算法; 振動頻率; 脈動壓力
中圖分類號:U441+.3; U443.3文獻標志碼: A文章編號: 1004-4523(2018)02-0300-08
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.013
引言
橋梁主梁斷面外形多具有邊角特征,流動分離復雜多變,其所產生的旋渦脫落,形成作用于結構上的氣動力,使其發生渦振、顫振等不利風致振動。隨著中國經濟活動與建筑技術的持續發展,大跨度橋梁建設項目日益增多,其結構柔性特征更為明顯,風敏感性進一步增強,風場與主梁斷面之間的流固耦合問題更為凸顯。因此,研究振動狀態下的橋梁節段氣動特征十分重要,有助于深入了解橋梁結構氣彈現象,具有重要的理論意義和工程價值。
當前,橋梁風振研究側重于主梁渦振特性及顫振穩定性研究[1],王騎等[2]以某流線型鋼箱梁斷面為研究對象,借助風洞試驗,深入研究其氣動外形對渦振和顫振性能的影響,結果表明,較小的斜腹板傾角(15°)可以抑制箱梁下風側旋渦的形成脫落,能大幅提升主梁顫振性能,消除渦振現象。錢國偉等[3]則針對Π型疊合梁展開一系列風洞試驗,研究其渦振性能并提出氣動改進措施,試驗結果指出圓形截面欄桿和改尖風嘴角度均有利于減小渦振振幅。劉健新等[4]、張偉等[5]還針對橋梁斷面氣動特性的雷諾數效應,展開一系列試驗研究。而相比于風洞試驗,數值模擬可以有效避免風洞縮尺試驗的不足,提供豐富的流場可視化圖像,實現多參數研究。因此,隨著計算設備和CFD方法的發展,數值模擬得到越來越廣泛的應用。丹麥的Walther和Larsen[6]率先基于離散渦方法(Discrete Vortex Method)模擬大海帶東橋主梁截面的渦振現象,并將豎向渦振振幅計算結果與風洞試驗結果比對,以驗證此類數值方法的可靠性。Frandsen[7]基于有限元方法,采用任意拉格朗日-歐拉模型,展開大海帶東橋顫振失穩性能研究,結論指出此類準鈍體主橋斷面顫振失穩與來流湍流及模擬結構尺度無關。Nieto等[8]采用非穩態雷諾平均方法(URANS)展開橋梁顫振導數方面的研究。國內方面,周志勇等[9]、劉天成等[10]分別采用有離散渦方法和Lattice-Boltsmann方法識別不同類型橋梁斷面形式的氣動參數。黃俐等[11]針對某類大高寬比橋梁節段風洞試驗所出現的兩個渦振鎖定區現象,采用數值模擬方法研究相關機理,通過提取尾流旋渦和氣動力,發現兩類鎖定區尾流渦脫轉換以及各自的相位差變化特征。孫芳錦等[12]采用強耦合計算方法,展開大跨度懸索橋的風振響應和顫振分析,研究結論指出流固耦合效應加深了結構的不穩定性。
上述針對橋梁斷面風振性能的研究多集中于對斷面氣動導數或渦振振幅、起振風速等參數性能的研究,對于橋梁斷面表面壓力時空分布特征、流場特征以及氣動力系數隨振動頻率、振幅的變化特征并未作詳細展開。同時,上述數值模擬研究中的所采用的CFD方法,均借助動網格技術實現振動邊界繞流問題的求解[13]。此類方法需要在每一時間步重復劃分網格,計算耗費較高,尤其針對具有復雜幾何外形的主梁斷面,不利于系統計算的展開。相比之下,浸入邊界方法(IBM,Immersed Boundary Method)利用力源擬化邊界的思想,直接可在靜止網格體系中實現振動鈍體的邊界再現,略去網格再生步驟,能夠顯著減輕計算負擔,且保證較好的計算精度。早期IBM的研究多集中于算法穩定性改進及基礎鈍體繞流模擬研究[14-15],后期僅在輪機、活塞等工程簡化研究問題中作出嘗試[16-17],少有針對土木結構流固耦合繞流模擬的應用。因此,利用浸入邊界方法,系統地開展振動二維橋梁斷面繞流研究,亦具有較高的科學應用價值。
本文基于IBM核心概念搭建數值模型,以大海帶東橋為研究對象,模擬雷諾數Re=7.5×103時,不同豎向強迫振動頻率及振幅下橋梁斷面繞流,其運動軌跡為 y(t)=Asinφ=Asin(2πfct),其中y(t)為物體軌跡,A為振幅,fc為強迫振動頻率,t為時間。通過氣動力系數、流場特征、表面壓力分布三個方面,研究不同振幅及振動頻率下橋梁斷面氣動性能變化規律,以得出影響振動橋梁繞流氣動特征的關鍵變量。
1數值模型
第2期楊青,等:考慮振動頻率及振幅變化影響的橋梁斷面氣動特征分析振 動 工 程 學 報第31卷本文數值模型以IBM為基礎,結合雙線性插值(Bi-linear interpolation method)和內部流體處理方法(Internal flow treatment),以實現橋梁斷面強迫振動繞流模擬。
1.1IBM控制方程
IBM利用流體與物體邊界相互作用的力學概念,將物體邊界簡化為作用于邊界點上的力源,并引入至Navier-Stokes方程中參加流場迭代計算,進而演化出邊界的幾何形狀和物理特性如下式:uixi=0(1)
uit+uiujxj=-1ρPxi+ν2uixjxj+1ρFi(2)式中ui,uj為流體速度,ρ為流體密度,P為壓力,ν為流體運動黏性系數,Fi即為邊界力源,施加于圖1中邊界點上。圖1浸入邊界示意圖
Fig.1Illustration of immersed boundary
邊界力源Fi采用虛擬邊界法(VBM,Virtual Boundary Method)構造形式,其力源概念更加清晰,反饋循環的應用也使其能夠實現較高的邊界數值精度,如下式所示Fi=αf∫t0ui(sur)-Vdesired dt′+
βfui(sur)-Vdesired(3)式中αf和βf為反饋系數項,其取值直接關系到邊界擬化效率;ui(sur)為邊界控制點處流體速度,由流體控制方程計算得出;Vdesired為物體邊界設定速度,靜止狀態時其值為零,若物體處于強迫振動狀態時,Vdesired可由振動方程計算得出;ui(sur)-Vdesired為邊界處流體速度與邊界設定速度的差異,表達式(3)正是基于此差異,通過反饋系數回饋出邊界力源使兩者速度接近,以滿足無滑移剛性邊界條件。內部流體則選用自由發展方法展開處理。
1.2振動邊界實現技術
IBM的計算核心在于獲取實時邊界控制點處流體速度ui(sur),用以構造邊界力源,進而迭代出鈍體外形。本次模擬對象為振動邊界,且計算網格采用交錯網格,邊界控制點很難與速度網格點重合,如圖2所示。
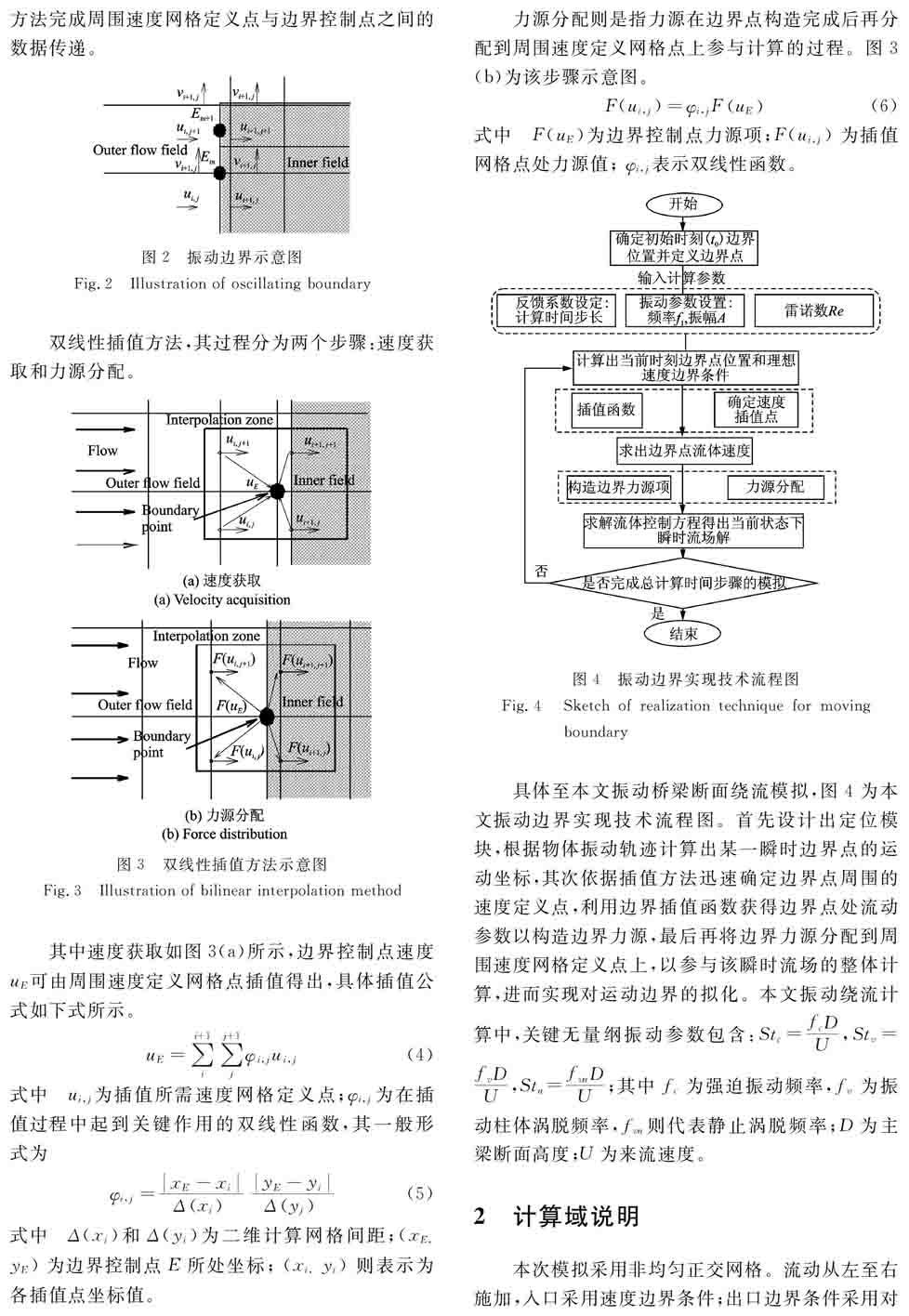
圖2中振動狀態下的邊界控制點E位置隨時間發生改變(Etn—Etn+1),此時邊界速度不能由流體控制方程直接求得。因此,為保證邊界控制點速度的實時獲取,需借助本節開始所介紹的雙線性插值方法完成周圍速度網格定義點與邊界控制點之間的數據傳遞。圖2振動邊界示意圖
Fig.2Illustration of oscillating boundary
雙線性插值方法,其過程分為兩個步驟:速度獲取和力源分配。圖3雙線性插值方法示意圖
Fig.3Illustration of bilinear interpolation method
其中速度獲取如圖3(a)所示,邊界控制點速度uE可由周圍速度定義網格點插值得出,具體插值公式如下式所示。uE=∑i+1i∑j+1jφi,jui,j(4)式中ui,j為插值所需速度網格定義點;φi,j 為在插值過程中起到關鍵作用的雙線性函數,其一般形式為φi,j=xE-xiΔxiyE-yiΔyj(5)式中Δ(xi)和Δ(yi)為二維計算網格間距;(xE, yE) 為邊界控制點E所處坐標; (xi, yi) 則表示為各插值點坐標值。
力源分配則是指力源在邊界點構造完成后再分配到周圍速度定義網格點上參與計算的過程。圖3(b)為該步驟示意圖。F(ui,j)=φi,jFuE(6)式中F(uE)為邊界控制點力源項;F(ui,j) 為插值網格點處力源值; φi,j 表示雙線性函數。圖4振動邊界實現技術流程圖
Fig.4Sketch of realization technique for moving boundary
具體至本文振動橋梁斷面繞流模擬,圖4為本文振動邊界實現技術流程圖。首先設計出定位模塊,根據物體振動軌跡計算出某一瞬時邊界點的運動坐標,其次依據插值方法迅速確定邊界點周圍的速度定義點,利用邊界插值函數獲得邊界點處流動參數以構造邊界力源,最后再將邊界力源分配到周圍速度網格定義點上,以參與該瞬時流場的整體計算,進而實現對運動邊界的擬化。本文振動繞流計算中,關鍵無量綱振動參數包含:Stc=fcDU,Stv=fvDU,Stn=fvnDU;其中fc為強迫振動頻率,fv為振動柱體渦脫頻率,fvn則代表靜止渦脫頻率;D為主梁斷面高度;U為來流速度。
2計算域說明
本次模擬采用非均勻正交網格。流動從左至右施加,入口采用速度邊界條件;出口邊界條件采用對流邊界條件:ut+umu=0;即流動變量除壓力項外其余的邊界梯度值為零。上下邊界條件設定為無摩擦邊界:uy=0,Py=0,v=0;力源反饋系數取值為αf=-1.6×105;βf=-60。
計算域近壁面網格尺寸Δh=0.005D,時間步長取Δt=5×10-5,其中D為主梁斷面高度。入口至斷面迎風面風嘴處距離為20D,出口邊界距迎風面風嘴處長度為60D,以保證尾流能順利放出計算域。計算域高度為H,DH=130,滿足阻塞率要求。考慮到斷面豎向振動,沿振動方向在斷面上下表面各設置1倍柱體高度的均勻網格區域,格子大小統一選為0.005D,以便于表面流動細節的捕捉。格子延伸率設定為1.02~1.08,網格總數為850×930。計算域布置如圖5所示。圖5振動橋梁節段計算域示意圖
Fig.5Illustration of calculation domain for oscillating bridge section3數值驗證
為驗證本文程序的可靠性,首先利用其模擬雷諾數Re=7.5×103,振幅A=0的靜止橋梁節段繞流。圖6 0°攻角主梁繞流矢量及渦量圖
Fig.6Vector and vortex contour of bridge section at 0° wind attack angle
圖6(a)中橋梁邊界為圖形后處理軟件Tecplot通過設置速度之和Velcoity Magnitude為10-5而勾勒出的速度邊界。圖中來流速度矢量在橋梁邊界發生的流動分離,也更好地證明了本次橋梁斷面模擬的正確性。斷面內由于邊界封閉較好,無速度矢量存在。結合圖6(b)繞流渦量圖分析,可以看出此時0°攻角下大海帶橋由于其相對平滑的造型,不存在劇烈的流動分離和渦脫。迎風面處流動分離尺度并不大,斷面上下表面的流動幾乎都緊貼著壁面,邊界層很薄,這也解釋了此次模擬在近壁面區域加密格子的處理方式。圖6(a)流場矢量圖中也可以看出,斷面背后尾流渦更靠近箱梁下側,但由于回流區較短,渦的影響范圍并不大,尾流區呈現規律性旋渦脫落,整個流場基本為對稱流場。
為進一步驗證本次模擬的準確性,繼續展開氣動力分析。本文氣動力定義形式為:阻力系數CD=2FDρU2B,升力系數CL=2FLρU2B,升力矩系數CM=2FMρU2B2,其中B為橋梁斷面寬度。
本次計算0°攻角下時均阻力系數
表1大海帶東橋0°攻角氣動力系數識別結果
Tab.1Aerodynamic coefficients of Great Belt Bridge at 0° wind attack angle
ReferenceModel Re
Fig.7Spectrum amplitude of lift coefficients at 0° wind attack angle4振動橋梁斷面繞流模擬
不同振動頻率及振幅下,主梁氣動特性分析首先關注氣動力系數。本文模擬在斷面外形構造完成且流場穩定后,展開數據收集統計。
圖8為不同振動頻率下橋梁斷面升力系數時程,可以看出,升力系數時程曲線均體現出正弦特性,反映了與物體運動較強的相關性。圖8升力系數時程圖
Fig.8Time history curve of lift coefficients
在此基礎上,統計出氣動力系數隨振動要素(振動頻率、振幅)的變化曲線,如圖9~11所示。圖中可以看出,振動狀態下斷面氣動力系數變化范圍也大致符合靜止狀態大海帶東橋氣動力文獻數據(
圖9阻力系數變化曲線(Stc=0.1~0.25; A=0.14D~0.25D)
Fig.9Variation curve of drag coefficients(Stc=0.1~0.25; A=0.14D~0.25D)
圖10為大海帶東橋斷面升力系數隨振動變化曲線圖,升力系數在Stc=0.1工況之后呈現明顯的上升趨勢,在振動頻率為自然渦脫頻率時(Stn=0.15)時均升力系數位于零值附近,振幅越大其歸零效應越明顯(A=0.25D),貼近于靜止狀態下升力系數計算結果;隨后在Stc=0.2又回歸到原有數值范圍附近,當振動頻率Stc=0.25時,其升力系數出現明顯的反向變化,振動幅值越高,其反向變化幅度就越大,在振幅A=0.20,0.25處,均出現升力系數反向。
圖10升力系數變化曲線(Stc=0.1~0.25; A=0.14D~0.25D)
Fig.10Variation curve of lift coefficients(Stc=0.1~0.25; A=0.14D~0.25D)
圖11升力矩系數變化曲線(Stc=0.1~0.25; A=0.14D~0.25D)
Fig.11Variation curve of lifting moment coefficients(Stc=0.1~0.25; A=0.14D~0.25D)
圖11升力矩系數在振幅較小時(A=0.14D),不隨振動頻率的改變而發生較大的變化,基本保持恒定狀態;此后當振幅升高時,升力矩系數會在自然渦脫頻率(Stn=0.15)之后迅速減小,振幅越大其變化效應越加明顯;當振動頻率Stc=0.25時,升力矩系數再次回歸到原有范圍內。
為更細致分析和探討斷面氣動力系數變化特征,將其表面分段標注,示意圖如圖12所示。圖12橋梁斷面分段示意圖
Fig.12Illustration of segment for bridge section
圖13為橋梁斷面在振動幅值A=0.20D時,不同振動頻率下的表面壓力分布圖。圖13橋梁斷面表面壓力分布(A=0.2D)
Fig.13Surface pressure distribution of bridge section(A=0.2D)
先針對阻力系數,觀察斷面風嘴處(AB,AF,CD,DE)隨不同振動頻率下的分布。結果表明:不同于矩形柱前緣壓力分布在不同振動頻率下基本一致的現象,橋梁斷面前后緣風嘴表面壓力分布均隨振動頻率而發生變化;斷面前后緣表面壓力分布基本呈現隨振動頻率升高而逐漸下降的趨勢但幅度不大;振動頻率Stc=0.10與0.15時,迎風面下翼緣AF表面壓力分布基本一致,但0.15之后斷面表面壓力分布變化劇烈。因此,推測出迎風面下翼緣是決定橋梁斷面阻力系數的關鍵因素。
對于升力系數,斷面上表面壓力分布不隨隨振動頻率而變化,風嘴上緣壓力隨振動頻率呈現漸進式變化,但風嘴下緣以及斷面下表面壓力分布在Stc=0.25時出現突變現象(AF,FE,ED),這也可能是升力系數在振動高頻處出現反向變化的原因。
圖14為不同振幅和振動頻率下橋梁斷面瞬時渦量圖,此時斷面均處于流場中心位置。圖中反映出:同一振幅下,不同振動頻率時渦量分布圖變化較為明顯;振動頻率相同,僅振幅不同時斷面渦量分布特征則基本相似。為確定此類氣動特性,提取本次模擬中橋梁上下表面脈動壓力分布,以進一步分析探討。圖14振動橋梁斷面渦量圖
Fig.14Vortex contour of oscillating bridge section
圖15為不同振幅和振動頻率下(Stc=0.1~0.2; A=0.14D~0.2D),上下表面脈動壓力值分布曲線。結果表明:同一振幅下,表面脈動壓力值隨振動頻率增大而總體升高,表面分布差異也隨之變大;迎風面風嘴前緣處脈動壓力值一直處于較高水平且變化最大;脈動壓力值在表面后緣的變化相對較小,其上表面后緣基本無變化。
圖15振動狀態橋梁表面脈動壓力分布(A=0.14D~0.20D, Stc=0.1~0.2)
Fig.15Fluctuating pressure distribution of oscillating bridge section(A=0.14D~0.20D, Stc=0.1~0.2)
當振動頻率一致,振幅增高時,表面脈動壓力值亦會增大,但脈動壓力沿表面分布特性曲線基本保持一致。這說明決定表面脈動壓力分布特性的主要因素是振動頻率,振幅只是會影響其脈動值的大小,對表面脈動壓力分布特性無過大影響。
5結束語
本文基于IBM算法概念,搭建出可在靜止網格完成豎向強迫振動橋梁斷面繞流模擬的數值計算程序。通過流場特征、氣動力系數、表面壓力分布等方面,著重探究振動要素(振動頻率及振幅)對橋梁斷面氣動特性的影響,以得出影響其氣動特征的關鍵變量,具體結論如下:
(1)主梁阻力系數在接近自然頻率處附近發生峰值現象;升力系數在自然頻率處減弱,但此后隨著振動頻率的增加而加強,并在高頻處發生反向。
(2)迎風面下翼緣是決定橋梁斷面阻力系數和升力系數隨振動頻率變化的關鍵因素,橋梁結構在不同振動頻率處呈現不同的渦量分布,但是在同一振動頻率處僅改變物體運動振幅,斷面流場渦量分布基本保持不變。
(3)表面脈動壓力值也反映出相同的結論,振動頻率是決定表面脈動壓力分布的重要因素,振幅只會改變其值的大小,不影響其脈動壓力分布特性。
在此研究基礎之上,后期將開展包含細部構件的典型橋梁斷面風振數值模擬,利用浸入邊界數值程序的便捷性,深化計算風工程對實際工程結構氣動特性的研究。參考文獻:
[1]周奇, 朱樂東. 平行雙幅斜拉橋渦振特性氣彈模型試驗研究[J]. 振動工程學報, 2013, 26(4):522—530.
ZHOU Qi, ZHU Le-dong. Study on vortex-induced oscillation of parallel bridge with twin-decks via aero-elastic model test [J]. Journal of Vibration Engineering, 2013, 26(4):522—530.
[2]王騎, 廖海黎, 李明水,等. 流線型箱梁氣動外形對橋梁顫振和渦振的影響[J]. 公路交通科技, 2012, 29(8):44—50.
WANG Qi, LIAO Haili, LI Mingshui, et al. Influence of aerodynamic shape ofsStreamline box girder on bridge flutter and vortex-induced vibration [J]. Journal of Highway and Transportation Research and Development, 2012, 29(8):44—50.
[3]錢國偉, 曹豐產, 葛耀君,等. Π型疊合梁斜拉橋渦振性能及氣動控制措施研究[J]. 振動與沖擊, 2015, 34(2):176—181.
QIAN Guowei, CAO Fengchan, GE Yaojun, et al. Vortex-induced vibration performance of a cable-stayed bridge with Π shaped composite deck and its aerodynamic control measures [J]. Journal of Shock and Vibration, 2015, 34(2):176—181.
[4]劉健新, 崔欣, 李加武. 橋梁斷面表面壓力分布及Strouhal數的雷諾數效應[J]. 振動與沖擊, 2010, 29(4):146—149.
LIU Jian-xin, CUI Xin, LI Jia-wu. Reynolds number effect of surface pressure distribution and Strouhal number of a typical bridge deck section [J]. Journal of Shock and Vibration, 2010, 29(4):146—149.
[5]張偉, 魏志剛, 楊詠昕,等. 基于高低雷諾數試驗的分離雙箱渦振性能對比[J]. 同濟大學學報(自然科學版), 2008, 36(1):6—11.
ZHANG Wei, WEI Zhigang, YANG Yongxin,et al. Comparison and analysis of vortex induced vibration for twin-box bridge sections based on experiments in different Reynolds numbers [J]. Journal of Tongji University (Natural Science), 2008, 36(1):6—11.
[6]Larsen A, Walther, J H. Aero-elastic analysis of bridge girder sections based on discrete vortex simulations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67: 253—265.
[7]Frandsen J B. Numerical bridge deck studies using finite elements. Part I: flutter[J]. Journal of Fluids and Structures, 2004, 19(2): 171—191.
[8]Nieto F, Owen J S, Hargreaves D M, et al. Bridge deck flutter derivatives: Efficient numerical evaluation exploiting their interdependence [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015,136: 138—150.
[9]周志勇. 離散渦方法用于橋梁截面氣動彈性問題的數值計算[D]. 上海:同濟大學, 2001.
ZHOU Zhi-yong. Numerical calculation of aeroelastie problems in bridges by discrete vortex method [D]Shanghai: Tongji University, 2001.
[10]劉天成, 葛耀君, 曹豐產. 基于Lattice Boltzmann 方法的方柱繞流[J]. 同濟大學學報, 2008, 36(8):1028—1033.
LIU Tiancheng, GE Yaojun, CAO Fengchan. Simulation of flow around square cylinder based on lattice Boltzmann method[J]. Journal of Tongji University (Natural Science), 2008, 36(8):1028—1033.
[11]黃俐, 周帥, 梁鵬. 橋梁斷面兩個渦振鎖定區間的數值模擬研究[J]. 振動與沖擊, 2016, 35(11):47—53.
HUANG Li, ZHOU Shuai, LIANG Peng. Numerical simulation for two separated vortex-induced vibration lock-in intervals of bridge sections [J]. Journal of Shock and Vibration, 2016, 35(11):47—53.
[12]孫芳錦, 梁爽. 考慮流固耦合作用的大跨度橋梁風振響應研究[J]. 公路交通科技, 2015, 32(7):84—91.
SUN Fang-jin, LIANG Shuang. Study on wind-induced vibration responses of long-span Bridge considering fluid-solid coupling [J]. Journal of Highway and Transportation Research and Development, 2015, 32(7):84—91.
[13]Huang L, Liao H, Wang B, et al. Numerical simulation for aerodynamic derivatives of bridge deck[J]. Simulation Modelling Practice and Theory, 2009, 17(4): 719—729.
[14]Luo H, Dai H, PJSAF de Sousa, et al. On the numerical oscillation of the direct-forcing immersed-boundary method for moving boundaries[J]. Computers & Fluids, 2012, 56(4): 61—76.
[15]Lee J,You D. An implicit ghost-cell immersed boundary method for simulations of moving body problems with control of spurious force oscillations[J]. Journal of Computational Physics, 2013, 233: 295—314.
[16]Choi J I, Oberoi R C, Edwards J R, et al. An immersed boundary method for complex incompressible flows[J]. Journal of Computational Physics, 2007, 224(2): 757—784.
[17]Tyagi M, Acharya S. Large eddy simulation of turbulent flows in complex and moving rigid geometries using the immersed boundary method. [J]International Journal for Numerical Methods in Fluids, 2005, 48(7): 691—722.
[18]Taylor I J, Vezza M. Analysis of the wind loading on bridge-deck sections using a discrete vortex method[C]. Wind Engineering into the 21st Century, Balkema, Rotterdam, 1999: 1345—1352.
[19]Enevoldsen I, Pederson C, Hansen SO, et al. Computational wind simulations for cable-supported bridges[C]. Wind Engineering into the 21st Century, 1999, 2: 1265—1270.
Analysis of aerodynamic characteristics of bridge section with varied
oscillating frequency and amplitude
YANG Qing1,2, CAO Shu-yang3
(1. College of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China;
2. Key Laboratory of Jiangsu Province High Tech. Design of Wind Turbine, Nanjing University of Aeronautics
and Astronautics, Nanjing 210016, China;
3. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China )
Abstract: In order to investigate the influence of oscillating frequency and amplitude variation on the aerodynamic characteristics of bridge section, the immersed boundary method, which can compute the moving boundary on the stable grid, is adopted in this paper to compile numerical calculation program. Then the simulation of flow around forced oscillating bridge section in transverse sinusoidal mode is carried out, in which the range of oscillating amplitude (A) is varied from 0.14D to 0.25D and frequency Stc is from 0.1 to 0.25. The results indicate that mean drag coefficients of the oscillating bridge section with different oscillating amplitudes all reach the max value near the stable vortex shedding. Whereas mean lift coefficients of the oscillating bridge section all back to zero at this point. The lower surface of windward may be viewed as a critical factor to determine the mean drag and lift coefficient of the bridge section. Vortex contours of the bridge section appear differences at varying oscillating frequency, while vortex contours of bridge section retain constant at different oscillating amplitudes with the same frequency. Oscillating frequency is the crucial factor to determine the fluctuating pressure distribution on surface. Oscillating amplitude only change the magnitude of fluctuating pressure, not its distribution characteristics.
Key words: bridge section; wild-induced vibration; immersed boundary algorithm; oscillating frequency; fluctuating pressure

