平面細長梁基于無網格徑向基點插值的絕對節點坐標法

陳淵釗 章定國 黎亮

摘要： 為了消除或減弱傳統絕對節點坐標法（Absolute Nodal Coordinate Formulation，ANCF）中縮減梁單元的“失真現象”，構造了一種適用于描述柔性梁絕對位形的無網格徑向基點插值 （Radial Point Interpolation Method， RPIM）形函數，提出了柔性梁基于無網格RPIM的ANCF法。傳統ANCF梁單元在描述純彎曲懸臂梁的位形（一段圓弧）時，即便獲得精確的單元節點坐標，通過梁單元插值得到的位形與懸臂梁的實際位形存在差異，即失真現象，懸臂梁越彎曲該差異越明顯，失真越大。失真導致偽應變的產生，極大地影響數值求解的精度。而RPIM法采用一組場節點離散問題域，通過計算點支持域內的場節點構造形函數，計算點一般位于支持域的中心區域，不同計算點之間的支持域有較多重合的部分，加強了節點之間的聯系，能更合理、準確地描述絕對位形，能有效減小失真。研究表明：基于RPIM的ANCF法較傳統ANCF法精度更高、計算效率更快、對不等距分布節點的適應性更強，在大變形柔性多體系統動力學領域內具有推廣性。

關鍵詞： 多體系統動力學； 柔性梁； 絕對節點坐標法； 徑向基點插值法； 失真

中圖分類號： O313.7； O322 文獻標志碼： A 文章編號： 1004-4523（2018）02-0245-10

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.007

引 言

ANCF法最早由Shabana[1]于1996年提出，該方法直接從連續介質力學出發，推導得到的動力學方程具有常數質量陣、不存在離心力項和科氏力項等特點，是一種適用于求解大轉動、大變形動力學問題的方法[2-5]。一般地，ANCF法基于有限單元法，許多ANCF梁、板單元是通過多項式構造得到的[6-11]。然而Sanborn[12]發現三次多項式曲線的彎曲程度會影響參數點的分布，在曲線彎曲程度較大時會出現偽應變及曲線失真。張越[13]指出純彎曲的ANCF縮減梁單元在彎曲程度較大時存在軸向拉伸變形，即存在偽拉伸應變，并認為其原因為彎曲、拉伸應變相互耦合，提出相應的解耦方法以消除偽應變，但其形函數仍與ANCF縮減梁單元一致。而Hyldahl [14]使用ANCF矩形殼單元離散一個四分之一空心圓盤時，發現一些單元之間存在“空白”，即相鄰兩個單元彎曲的共用邊不重合，存在明顯的縫隙。空心圓盤和ANCF殼單元可以分別看成是矩形板、ANCF矩形單元在變形后的形狀，ANCF矩形單元基于精確的節點坐標插值得到的絕對位形與變形后的矩形板存在誤差，即失真現象，說明基于多項式的ANCF單元并不能很好地描述變形體的絕對位形。事實上，若給定一段圓心角較大的圓弧曲線（純彎曲懸臂梁的位形），將兩端端點的位置及梯度精確賦值給ANCF縮減梁單元節點坐標，通過單元插值得到的曲線與實際曲線會存在偏差，曲線越彎曲偏差越大，因此，單個ANCF一維梁單元并不能很好地描述大曲率的曲線，單元的位形不同于純彎曲細長梁的位形，即存在失真現象，從而使得單元中產生偽應變。

為避免偽應變的產生，應使ANCF精準地描述整個絕對位形，消除或減小失真，一般的解決方法便是大量增加單元數目，避免失真現象的產生，但這樣會大大增加計算的規模及耗時。因此，構造一種精確描述絕對位形的離散方法是非常有必要的。計算力學中除了有限元法（Finite Element Method， FEM）以外，仍有不少新發展起來的離散方法，如無網格法（Meshfree Method）[15]。無網格法是一種不依賴單元網格的離散方法，該方法采用一組點來離散求解區域，并應用計算點支持域內的場節點構造近似函數，可以使用較多的場節點來提高近似函數的連續性[15]。FEM法兩個相鄰單元的計算點之間的聯系僅僅依靠單元間的共同節點，而無網格法不同計算點之間的聯系則是依靠對應支持域重合部分的場節點，比單元的共同節點多得多，使得無網格法節點之間的聯系更加緊密，可以更好地描述變形場。而目前應用無網格法對絕對坐標場插值的研究尚未有報道。

現有的無網格法有多種，如再生核粒子法（Reproducing Kernel Particle Method， RKPM）[16-18]、無網格局部Perov-Galerkin法（Meshfree Local Perov-Galerkin Method， MLPGM）[19]、徑向基點插值法[20]等。其中Liu GR等 [15，20] 提出的RPIM具有魯棒性、高精度、Kronecker函數特性等特點，因此多被用于固體、流體力學問題的研究中[20-25]。杜超凡等成功將無網格法RPIM應用到柔性梁一次近似剛柔耦合模型[26]，并在柔性多體系統動力學問題上取得了良好的結果，說明無網格法在柔性多體系統動力學具有推廣性[26-28]。

鑒于無網格RPIM法的優勢，本文構造一種適用于描述柔性梁絕對位形的RPIM形函數，并基于連續介質力學和哈密頓原理建立平面細長梁系統的動力學方程，提出基于無網格RPIM的絕對節點坐標法。本文首先闡明ANCF縮減梁單元中失真現象的客觀存在性，通過與本文方法對比，分析偽應變產生原因，同時檢驗本文方法描述曲線的性能。再通過大變形靜力學、動力學算例，分析失真對傳統ANCF縮減梁單元精度的影響，同時比較說明本文方法精確處理大變形問題的精度及效率。

1 柔性梁的ANCF模型

本文研究對象為平面梁系統，采用Euler-Bernouli假設，不考慮剪切變形，并認為變形時梁的橫截面仍保持為平面且與中軸線垂直避免偽應變的產生，其實就是避免失真現象，但失真現象很難完全消除，僅能盡量減小失真的程度，所以需要增加離散的節點數。事實上，除了加密離散以外，還可以采用其他更合理的插值方法來減小失真。若取長度為3 m整圓，等長劃分三段，即取四節點，應用傳統ANCF法和本文方法進行插值，如圖4所示，傳統ANCF插值結果偏差較大，失真明顯，本文方法所得結果基本與圓重合，說明本文方法較傳統ANCF描述曲線更合理，失真的程度較傳統ANCF法小得多。表3給出了此時基于兩種方法求得的勢能。在傳統ANCF結果中，一個長度為1 m、曲率κ=2π/3單元的偽應變能為7.3985 J（如表2所示），三個單元的偽應變之和為22.1958 J，三個單元所得偽勢能為一個單元偽勢能的三倍，說明傳統ANCF單元之間聯系簡單，偽勢能較大，而本文方法所得結果較傳統ANCF法小得多，說明本文方法能有效減小失真。

4 仿真算例

由上一節得知ANCF描述彎曲較大的曲線時會失真，從而產生偽應變，這種現象對ANCF求解大變形問題時有著怎樣的影響，下面通過兩個簡單的例子進行討論。

4.1 受集中力矩作用的懸臂梁

考慮圖5所示的懸臂梁，梁末端受集中力矩τ的作用，研究其靜力學問題。梁長L=1.8 m，橫截面積A=2.5 cm2，截面慣性矩I=0.130 cm4，彈性模量E=68.95 GPa，密度ρ=2766.67 kg/m3，即梁參數選取與文獻[30-32]一致。

圖5 受集中力矩作用的懸臂梁

Fig.5 Cantilever beam under a moment

若梁末端受到力矩τ作用，力矩大小為τ=λEIL（51）其中λ為一常數。梁變形后的軸線為一段弧線，相應的曲率為κ=τLEI=λ（52） 當λ=2π時柔性梁的位形為一整圓，梁末端的水平、豎直方向上的絕對位移為0。選取不同數目的等距離分布的節點和不等距離分布的節點，對比本文方法和傳統ANCF法的差異。

等距分布的節點在梁上第i個節點的水平絕對坐標為xi=（i-1）Lm， i=1，…，m（53） 不等距分布的節點選取切比雪夫插值節點，梁兩端節點分布較密集，中間稀疏，梁上第i個節點的水平絕對坐標為xi=L2-L2cosi-1πm， i=1，…，m（54） 傳統ANCF法在使用這些節點時為相鄰兩節點構成一個單元。

在計算時，需忽略動能的影響，故靜力學方程為Qτ-F=0（55） 利用Newton-Raphson迭代即可求解靜力學方程。

表4為梁末端的水平方向的絕對位移，其解析解為0。從表4可以看出，在節點數較少時，傳統ANCF法計算結果不準確，本文方法計算結果仍有較高精度。此外，使用等距節點的傳統ANCF法仿真數值結果的精度要比使用不等距節點好，甚至高一個數量級，說明傳統ANCF法的計算精度受節點的分布情況影響很大，對網格依賴性高，而本文方法幾乎不受節點分布影響，對節點分布的依賴性很弱，由此可說明本文方法較傳統ANCF法對不等距分布的節點更具適應性，數值穩定性高。

表4 梁末端的水平方向絕對位移（單位：m）

Tab.4 Horizontal position of the free end of beam （Unit：m）節點數ANCFRPIM等距不等距等距不等距4-0.31663-0.36876-0.003530.003815-0.30480-0.514720.001210.000136-0.13772-0.428260.000080.000027-0.04940-0.29022-0.00006-0.000018-0.01829-0.16898-0.000070.000039-0.00767-0.08916-0.00003〖〗0.0000210-0.00368-0.04552-0.00001-0.00001 圖6為5節點等距分布時，應用兩種方法分別計算λ=0，0.5π，π，1.5π，2π時柔性梁的位形所得結果。如圖所示，λ=0.5π時，兩種方法基本與解析解吻合，說明求解柔性梁變形較小的靜力學問題時，兩種方法使用較少節點也可得到較為可信的結果，同時也驗證了本文方法的正確性。當λ=2π時，梁末端點A應與懸臂端點O重合，傳統ANCF法計算得到的點A位置與解析解相差較大距離，且梁的位形與解析解誤差明顯，本文方法與解析解的符合度較好，說明了本文方法的正確性，且精度較ANCF法高。事實上，λ=0.5π時，每個ANCF縮減梁單元的轉角θi很小，最大的僅有22.5°，所以此時的失真現象非常小，可以忽略；而λ=2π時，單元轉角θi最大的有74°，失真現象明顯，偽應變較大，會產生較大誤差，極大地影響了傳統ANCF法的求解精度。

圖6 受集中力矩作用時柔性梁的位形

Fig.6 Position of beam under a moment圖7為λ=2π時柔性梁的位形。此時，傳統ANCF法取10個節點形成單元計算，本文方法取5個節點計算。如圖7所示，傳統ANCF法取等距分布的節點時計算結果基本與解析解重合，此時最大的單元轉角θi有39°，失真現象基本可以忽略，而使用不等距節點時誤差較大，此時最大的單元轉角θi有60°，失真現象明顯；本文方法取等距節點和不等距節點均與解析解基本重合，與表4所得結論一致，說明傳統ANCF法的網格對精度影響很大，穩定性較低，本文方法則沒有這樣的缺陷。

圖7 λ=2π時柔性梁的位形

Fig.7 Position of beam under the moment （λ=2π）4.2 重力單擺

考慮如圖8所示的重力單擺，梁的材料參數仍與文獻[30-32]一致。

圖8 重力單擺

Fig.8 Gravity pendulum

圖9（a）和（b）分別為梁下落過程中末端的豎向、水平絕對位移，此時傳統ANCF法劃分四單元、本文方法取五節點。此時兩種方法仿真結果基本重合，ANCF縮減梁單元轉角θi最大值為0.15°，此時的梁在小變形狀態，說明在求解柔性梁小變形動力學問題時，兩種方法使用較少的單元（節點）數不會導致明顯的失真，可得到較好的數值結果。

圖9 自由單擺末端的絕對位移

Fig.9 Position of the free end of the pendulum

圖10 E=68.95 MPa時自由單擺末端的豎直絕對位移

Fig.10 Vertical position of free end of the pendulum

（E=68.95 MPa）圖10給出了E=68.95 MPa時柔性梁末端的豎向絕對位移。從圖10看，傳統ANCF 和RPIM分別在13個單元、10個節點時基本收斂，事實上，以某一點的位移作為收斂判斷的依據是不夠準確的，如圖11所示，傳統ANCF法使用30個單元和使用13、17個單元計算得到的2.5 s時柔性梁的位形有輕微的誤差，而與RPIM使用11個節點的計算結果更符合，說明RPIM精度更好。值得注意的是，傳統ANCF法使用13個單元時，彎曲最大的單元θi為39.9°；使用17個單元時，彎曲最大的單元θi為32.9°。說明少量增加單元個數并不能迅速減小某些單元的彎曲程度，而大量增加單元個數則大大增加了計算的耗時及規模，若采用RPIM則可有效提高計算精度。

圖11 2.5 s時柔性梁的位形

Fig.11 Deformed shape of the pendulum （t=2.5 s）

圖12 梁上每點的曲率

Fig.12 Curvature of points of the beam

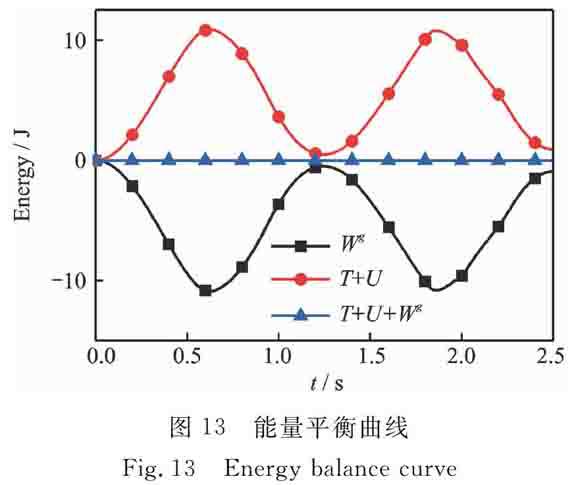
由于應力應變比位移更為重要，故以2.5 s時柔性梁上每點的曲率來衡量兩種方法的收斂性，如圖12所示，傳統ANCF法和RPIM分別在使用23個單元和14個節點時收斂。表5列出了兩種方法應用廣義α法[33]計算時的相對耗時，傳統ANCF法使用23個單元計算耗時比RPIM使用14個節點計算耗時要多得多，可表明RPIM精確處理大變形問題的高效性。圖13給出了柔性單擺下落過程中的能量變化曲線，系統的動能、勢能、應變能之和恒為零，即系統能量守恒，再次說明RPIM法的正確性。

表5 兩種方法的相對耗時

Tab.5 The relative time consuming of two methodsANCFRPIM19

單元23

單元29

單元12

節點14

節點15

節點1.4272.25784.26311.3421.494注：該算例采用廣義α法計算[33]

圖13 能量平衡曲線

Fig.13 Energy balance curve5 結 論

本文應用無網格RPIM法對平面柔性梁的絕對位形進行插值，利用支持域內的場節點所對應的徑向基函數及其導數來構造絕對位形的插值形函數，并通過哈密頓原理建立柔性梁系統的動力學方程，提出基于無網格RPIM的ANCF法。研究表明：

1） 傳統ANCF縮減梁單元在求解大變形問題時會存在失真現象，單元越彎曲失真現象就越明顯，產生的偽應變也越大，嚴重降低了數值求解的精度。故應控制每個單元的彎曲程度，加密網格、大量增加單元個數，但也同時大大增加了計算成本。

2） 本文方法能合理、準確地描述柔性梁變形后的絕對位形曲線，有效減小失真的程度，降低偽應變的影響。通過靜力學和動力學仿真算例可以說明：本文方法較傳統ANCF法精度更高、計算效率更快，對不等距分布節點的適應性更強。

參考文獻：

[1] Shabana A A. An absolute nodal coordinate formulation for the large rotation and deformation analysis of flexible bodies [R].Department of Mechanical and Industrial Engineering， University of Illinois at Chicago， 1996.

[2] Yakoub R Y， Shabana A A. Three dimensional absolute nodal coordinate formulation for beam elements： implementation and applications [J]. Journal of Mechanical Design， 2001， 123（4）： 614—621.

[3] Shabana A A， Yakoub R Y. Three dimensional absolute nodal coordinate formulation for beam elements： theory [J]. Journal of Mechanical Design， 2001， 123（4）： 606—613.

[4] Omar M A， Shabana A A. A two-dimensional shear deformable beam for large rotation and deformation problems [J]. Journal of Sound and Vibration， 2001， 243（3）： 565—576.

[5] Berzeri M， Shabana A A. Development of simple models for the elastic forces in the absolute nodal co-ordinate formulation [J]. Journal of Sound and Vibration， 2000， 235（4）： 539—565.

[6] Olshevskiy A， Dmitrochenko O， Dai M D， et al. The simplest 3-， 6- and 8-noded fully-parameterized ANCF plate elements using only transverse slopes [J]. Multibody System Dynamics， 2014， 34（1）： 23—51.

[7] Yan D， Liu C， Tian Q， et al. A new curved gradient deficient shell element of absolute nodal coordinate formulation for modeling thin shell structures [J]. Nonlinear Dynamics， 2013， 74（1-2）： 153—164.

[8] Dmitrochenko O， Mikkola A. Two simple triangular plate elements based on the absolute nodal coordinate formulation[J]. Journal of Computational and Nonlinear Dynamics， 2008， 3（4）： 041012.

[9] Gerstmayr J， Shabana A A. Analysis of thin beams and cables using the absolute nodal coordinate formulation [J]. Nonlinear Dynamics， 2006， 45（1-2）： 109—130.

[10]Dufva K E， Sopanen J T， Mikkola A M. A two-dimensional shear deformable beam element based on the absolute nodal coordinate formulation[J]. Journal of Sound and Vibration， 2005， 280（3-5）： 719—738.

[11]Dufva K， Shabana A A. Analysis of thin plate structures using the absolute nodal coordinate formulation[J]. Proceedings of the Institution of Mechanical Engineers， Part K： Journal of Multi-body Dynamics， 2005， 219（4）： 345—355.

[12]Sanborn G G， Choi J， Choi J H. Curve-induced distortion of polynomial space curves， flat-mapped extension modeling， and their impact on ANCF thin-plate finite elements [J]. Multibody System Dynamics， 2011， 26（2）： 191—211.

[13]張 越， 趙 陽， 譚春林，等. ANCF索梁單元應變耦合問題與模型解耦[J]. 力學學報， 2016， 48（6）： 1406—1415.

Zhang Yue， Zhao Yan，Tan Chunlin， et al. The strain coupling problem and model decoupling of ANCF cable/beam element[J]. Chinese Journal of Theoretical and Applied Mechanics，2016，48（6）：1406—1415.

[14]Hyldahl P， Mikkola A M， Balling O， et al. Behavior of thin rectangular ANCF shell elements in various mesh configurations [J]. Nonlinear Dynamics， 2014， 78（2）： 1277—1291.

[15]劉桂榮，顧元通. 無網格法理論及程序設計[M].王建明，周學軍，譯. 濟南：山東大學出版社，2007：45—133.

Liu G R， Gu Y T. An Introduction to Meshfree Methods and Their Programming[M]. Jinan：Shandong University Press， 2007：45—133.

[16]Chen J S， Pan C， Roque C M O L， et al. A lagrangian reproducing kernel particle method for metal forming analysis[J]. Computational Mechanics， 1998， 22（3）： 289—307.

[17]Chen J S， Pan C， Wu C T， et al. Reproducing kernel particle methods for large deformation analysis of non-linear structures[J]. Computer Methods in Applied Mechanics & Engineering， 1996， 139（1-4）： 195—227.

[18]Liu W K， Jun S， Zhang Y F. Reproducing kernel particle methods. Int J Numer Meth Eng[J]. International Journal for Numerical Methods in Fluids， 1995， 20（8-9）： 1081—1106.

[19]Xiong Y B， Long S Y. Local petrov-galerkin method for a thin plate[J]. Applied Mathematics and Mechanics， 2004， 25（2）： 210—218.

[20]Wang J G， Liu G R. A point interpolation meshless method based on radial basis functions[J]. International Journal for Numerical Methods in Engineering， 2002， 54（11）： 1623—1648.

[21]Cui X Y， Feng H， Li G Y， et al. A cell-based smoothed radial point interpolation method （CS-RPIM） for three-dimensional solids[J]. Engineering Analysis with Boundary Elements， 2015， 50： 474—485.

[22]Pilafkan R， Folkow P D， Darvizeh M， et al. Three dimensional frequency analysis of bidirectional functionally graded thick cylindrical shells using a radial point interpolation method （RPIM） [J]. European Journal of Mechanics / A Solids， 2013， 39（5）： 26—34.

[23]Gu Y T， Wang W L， Fu Q. An enriched radial point interpolation method （e-RPIM） for the analysis of crack tip[J]. Engineering Fracture Mechanics， 2010， 78（1）： 175—190.

[24]Chen S L， Li Y X. An efficient RPIM for simulating wave motions in saturated porous media[J]. International Journal of Solids & Structures， 2008， 45（25）： 6316—6332.

[25]Dai K Y， Liu G R， Han X， et al. Inelastic analysis of 2D solids using a weak-form RPIM based on deformation theory[J]. Computer Methods in Applied Mechanics & Engineering， 2006， 195（33）： 4179—4193.

[26]杜超凡， 章定國， 洪嘉振. 徑向基點插值法在旋轉柔性梁動力學中的應用[J]. 力學學報， 2015， 47（2）： 279—288.

Du Chaofan， Zhang Dingguo， Hong Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams[J]. Chinese Journal of Theoretical and Applied Mechanics， 2015，47（2）： 279—288.

[27]杜超凡， 章定國. 光滑節點插值法：計算固有頻率下界值的新方法[J]. 力學學報， 2015， 47（5）： 839—847.

Du Chaofan， Zhang Dingguo. Node-based smoothed point interpolation method： a new method for computing lower bound of natural frequency[J]. Chinese Journal of Theoretical and Applied Mechanics， 2015， 47（5）： 839—847.

[28]杜超凡， 章定國. 基于無網格點插值法的旋轉懸臂梁的動力學分析[J]. 物理學報， 2015，64（3）： 396—405.

Du Chaofan， Zhang Dingguo. A meshfree method based on point interpolation for dynamic analysis of rotating cantilever beams[J]. Acta Phys. Sin.， 2015， 64（3）： 396—405.

[29]章孝順，章定國，陳思佳，等. 基于絕對節點坐標法的大變形柔性梁幾種動力學模型研究[J].物理學報， 2016， 65（9）：148—157.

Zhang Xiaoshun， Zhang Dingguo， Chen Sijia，et al. Several dynamic models of a large deformation flexible beam based on the absolute nodal coordinate formulation[J]. Acta Phys. Sin.， 2016， 65（9）：148—157.

[30]陳思佳， 章定國， 洪嘉振. 大變形旋轉柔性梁的一種高次剛柔耦合動力學模型[J]. 力學學報， 2013， 45（2）：251—256.

Chen Sijia， Zhang Dingguo， Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation[J]. Chinese Journal of Theoretical and Applied Mechanics， 2013， 45（2）：251—256.

[31]李 彬， 劉錦陽. 大變形柔性梁系統的絕對坐標方法[J]. 上海交通大學學報， 2005， 39（5）： 827—831.

Li Bin， Liu Jinyang. Application of absolute nodal coordination formulation in flexible beams with large deformation[J]. Journal of Shanghai Jiaotong University， 2005， 39（5）： 827—831.

[32]章孝順， 章定國， 洪嘉振. 考慮曲率縱向變形效應的大變形柔性梁剛柔耦合動力學建模與仿真[J]. 力學學報，2016，48（3）：692—701.

Zhang X H， Zhang D G， Hong J Z. Rigid-flexible couple dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under larger deformation [J]. Chinese Journal of Theoretical and Applied Mechanics，2016，48（3）：692—701.

[33]Amold M， Brüls O. Convergence of the generalized-α scheme for constrained mechanical systems[J]. Multibody System Dynamics， 2007，18（2）：185—202.

An absolute nodal coordinate formulation based on

radial point interpolation method for planar slender beams

CHEN Yuan-zhao， ZHANG Ding-guo， LI Liang

（School of Science， Nanjing University of Science and Technology， Nanjing 210094， China）

Abstract： In order to alleviate or eliminate the ‘distortion phenomenon of the deficient beam elements in the traditional absolute nodal coordinate formulation （ANCF）， an ANCF based on radial point interpolation method （RPIM） for flexible beams is proposed in which a new RPIM shape functions are constructed to describe the absolute configuration of flexible beams. For a pure bending cantilever beam （an arc）， there is always difference between configuration of the beams by using the gradient deficient beam elements and the actual configuration of the beam in the traditional ANCF. The difference， namely ‘distortion phenomenon， becomes more obvious with the increase of the bending deformation of the beam， which may cause the pseudo strain and have serious influence on accuracy of numerical solution. In the present method， the RPIM is used to discretize the deformation field through a set of field nodes and the shape functions are generally established based on field nodes within a support domain of the calculating point. The calculating points are generally located in the central region of the support domain， and the support domain of different calculating points can have more coincident parts. Thus， the connection between field nodes is strengthened， which makes the method describe the configuration in more reasonable and effectively alleviate influence of the distortion and pseudo strain. The simulation results show that the proposed method has higher calculation accuracy and efficiency and is more adaptive for the non-equidistant nodes compared with the traditional ANCF， which can be further extended in the dynamic field of flexible multi-body system.

Key words： multibody dynamics； flexible beam； absolute nodal coordinate formulation； radial point interpolation method； distortion