雙參平面內單級直齒圓柱齒輪系統動力特性綜合分析

田亞平 褚衍東 饒曉波

摘要： 為揭示非線性直齒圓柱齒輪系統分岔、嚙合沖擊、脫嚙和動載系數間的耦合關系，在時變嚙合剛度幅值系數與無量綱頻率參數平面內用PNF法和延續算法對單級齒輪系統的動力學模型求解獲其周期/沖擊、脫嚙占空比、齒背嚙合比、動載系數偽彩圖。研究表明：幅值系數和頻率是影響分岔、沖擊、脫嚙、動載系數的主要因素，隨幅值系數遞增系統經倍化、Hopf、激變、擦切、鞍結分岔方式由周期運動通向混沌，并導致嚙合沖擊、脫嚙占空比和動載系數增大；混沌、擬周期運動和嚙合沖擊現象出現在共振頻率附近，其脫嚙、動載系數在該處出現極值。雙參平面內綜合動力特性轉遷規律為齒輪結構設計參數優化提供理論參考。

關鍵詞： 非線性振動； 單級齒輪傳動系統； 動力特性； PNF數值法； 雙參平面

中圖分類號： O322； TH132.425文獻標志碼： A文章編號： 1004-4523（2018）02-0219-07

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.004

引 言

齒輪傳動廣泛應用于各類機械裝置中，其非線性動力學行為是影響齒輪疲勞壽命的主要因素。Kahraman等[1]考慮齒側間隙和誤差激勵因素建立了單自由度單級齒輪系統動力學模型，發現了次諧響應和混沌響應。Vinayak等[2]研究了齒輪嚙合綜合傳遞誤差對系統非線性動力學行為的影響。劉曉寧[3]等用增量諧波平衡法對三自由度齒輪系統周期運動進行分析并判穩。茍向鋒[4]用相圖、Lyapnuov指數譜、Poincaré截面法找出了三自由度單級齒輪副隨參數變化通向混沌運動的途徑。王曉筍[5]等研究了含磨損故障的單級齒輪傳動系統的分岔行為及通向混沌的途徑。

PNF法（Poincaré-Newton-Floquet）是一種結合Floquet穩定性理論的周期運動求解、判穩同步進行的高效數值方法。PNF法在非線性動力學方面獲得了大量研究成果。羅躍綱[6]研究含裂紋和碰磨耦合故障的轉子系統周期運動的穩定性問題，韓清凱[7-8]研究碰磨轉子系統的周期運動穩定性問題，李同杰[9]研究行星齒輪傳動系統周期運動的穩定性問題，楊振 [10] 等研究正交面齒輪傳動系統分岔特性，田亞平[11]等研究了單級齒輪系統的周期運動及穩定性問題。上述成果均是單參下系統的分岔特性及周期運動穩定性問題，無法全面了解多參數耦合對系統動力特性的影響。雙參平面內研究非線性動力特性能理清系統參數之間的耦合關系并確定穩定運行的參數范圍，為實際工程中齒輪機構的參數選擇提供理論指導。茍向鋒等[12-13]采用胞映射和逃逸算法研究了雙參平面內純扭轉齒輪副的分岔特性和齒輪-轉子系統扭轉振動系統的周期運動及分岔特點。但綜合運用PNF法和延續算法研究齒輪系統在雙參平面內綜合動力特性（分岔、嚙合沖擊、脫嚙及動載系數）的文獻還鮮有報道。

本文以單級直齒圓柱齒輪系統的動力學模型為研究對象，用PNF法和延續算法對系統的周期運動、分岔、嚙合沖擊、脫嚙及動載系數進行求解，獲得時變嚙合剛度幅值系數和無量綱頻率雙參平面偽彩圖，探尋其動力特性隨參數轉遷的規律和耦合匹配關系。

第2期田亞平，等： 雙參平面內單級直齒圓柱齒輪系統動力特性綜合分析振 動 工 程 學 報第31卷 1 單級直齒圓柱齒輪系統非線性動力學模型 單級直齒圓柱齒輪傳動系統動力學模型如圖1所示。圖中，主從動齒輪的質量、轉動慣量、基圓半徑、扭轉角位移和輸入輸出扭矩用mgi，Igi，rgi，θgi，Tgi（i=1，2）表示；主從動齒輪支承軸承的間隙、阻尼、線性剛度、作用于軸承的徑向預載荷和徑向位移用bi，cbi，kbi，Fbi，ygi表示。時變嚙合剛度、齒側間隙、嚙合線性阻尼、綜合誤差用kh（t），2bh，ch，e（t）表示。

圖1 單級直齒圓柱齒輪傳動系統非線性模型

Fig.1 The nonlinear model of a single-stage spur gear system

定義無量綱齒輪嚙合的動態傳動誤差與靜態傳動誤差的差值y3

y3（τ）=[rg1θg1（τ）-rg2θg2（τ）+yg1-

yg2-e（τ）]/bc（1）

式中 bc為特征長度。

由文獻[3]知其系統的無量綱動力學方程為

1=-fb1-2ζ111-2ζ133-k11f（y1，b1）-

k13（τ）f（y3，b3）

2=fb2-2ζ222+2ζ233-k22f（y2，b2）+

k23（τ）f（y3，b3）

3=fm+fah1Ω2cos（Ωτ）+1-2-2ζ333-

k33（τ）f（y3，b3）（2）

式中 yi（i=1，2）為軸承無量綱徑向位移，yi=ygi/bc（i=1，2）；ζij（i，j=1，2，3）為阻尼比，ζij=cij/（2mijΩn），Ωn為系統固有頻率，Ωn=km/me，km為嚙合剛度平均值，me為嚙合等效質量。fbi為無量綱軸承徑向預載荷，fbi=Fbi/（mgiΩ2nbc）。fm為無量綱齒輪嚙合平均激勵力，fm=Tg1/（rb1meΩ2nbc）。fah1為無量綱內部激勵動載系數， fah1=ea/（mebc）。k33（τ）=1+αcos（Ωτ），k13（τ）= k23（τ）= k33（τ）/4，α為嚙合剛度幅值系數，Ω為無量綱頻率，Ω=Ωh/Ωn，Ωh為嚙頻。Kii= Ω2bi/Ω2n， Ωbi為軸頻，Ωbi=kbi/mgi。τ為無量綱時間，τ=Ωnt。f（yi，bi）為間隙非線性函數，bi=bhi/bc。f（yi，bi）=yi-bi，yi>bi

0，yi≤bi

yi+bi，yi<-bi（3）式中 bi為齒側和軸承支承的無量綱間隙。

對系統（2）進行降階處理，用狀態變量{x1，x2，…，x6}替代y1，1，…，y3，3，則系統（2）的狀態空間方程轉化為

1=x2

2=-fb1-2ζ11x2-2ζ13x6-k11f（x1，b1）-

k13（τ）f（x5，b3）

3=x4

4=fb2-2ζ22x4+2ζ23x6-k22f（x3，b2）+

k23（τ）f（x5，b3）

5=x6

6=fm+fah1Ω2cos（Ωτ）+2-4-2ζ33x6-

k33（τ）f（x5，b3）（4）

2 動力特性分析參數〖*2〗2.1 脫嚙占空比和齒背嚙合比 由文獻[14]知，齒輪嚙合中存在無沖擊、齒面擦切、脫嚙單邊沖擊、齒背擦切和齒背嚙合雙邊沖擊，其沖擊類型（impact=0，1，2）和脫嚙狀態由最小嚙合綜合誤差xmin與齒側間隙b來判斷，其表達式為

impact=0，xmin>b無沖擊，無脫嚙

0，xmin=b齒面擦切，無脫嚙

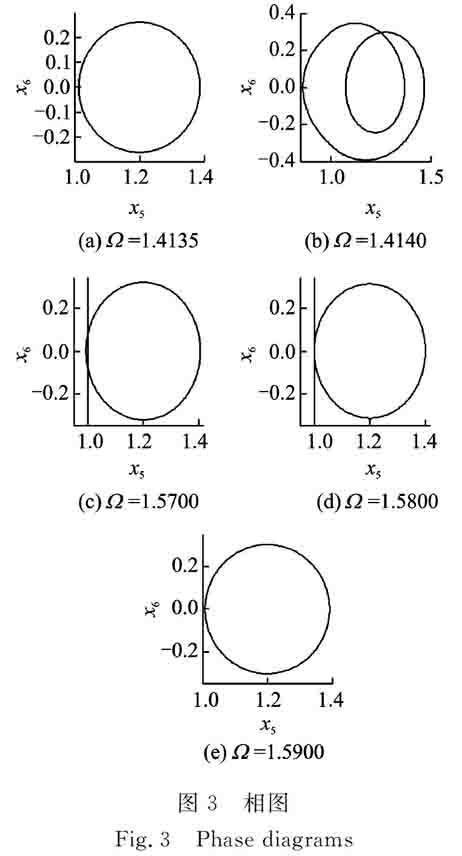
1，xmin

1，xmin=-b齒背擦切，脫嚙

2，xmin<-b雙邊沖擊，齒背接觸 （5）

脫嚙或齒背嚙合下，齒面產生的拍擊和附加動載荷是導致嚙合狀態惡化的主要因素。脫嚙占空比和齒背嚙合比用來表征齒輪脫嚙狀態惡化情況。設齒輪在一個嚙合周期T內脫嚙時間為t1，齒背嚙合時間為t2，則脫嚙占空比DC1和齒背嚙合比DC2為DC1=t1/T

DC2=t2/T（6）2.2 動載系數

在齒輪強度計算中，為考慮齒輪振動導致嚙合力增大的影響因數定義動載系數。動載系數受軸承剛度、齒輪箱結構、載荷狀態、潤滑劑等因素影響，其計算十分復雜，為了突出間隙和時變剛度對動載系數的影響，定義動載系數為周期內最大嚙合力與平均嚙合力的比值G=FdmaxFm=K（t）f（y3，b3）+C3Fmmax（7）式中 Fdmax為嚙合周期內最大嚙合力，Fm為平均嚙合力，經無量綱化為DLC=（∑3i=1ki3（τ）f（x5，b3）+∑3i=1ζi3x6）/fmmax（8）3 系統非線性動力特性綜合分析

在雙參平面內，為分析系統（4）的非線性動力綜合特性及其轉遷規律，取仿真參數：ζ11=ζ22=0.02，ζ13=ζ23=0.0125，ζ33=0.05，k11=k22=1.25，fah1=0.05，fb1= fb2=0.1，b1=b2=0，b3=1，仿真初值均取為0。無量綱平均載荷fm的大小表征了齒輪系統載荷狀態，本文中fm=0.2代表齒輪輕載運行狀態。無量綱頻率Ω∈[1，2]表征齒輪處于中高速運動狀態。即仿真參數表征中高速輕載狀態下齒輪系統動力學綜合特性。

3.1 PNF法系統分岔類型的判別及追蹤

PNF法分岔、追蹤、判穩方法如下：

（1）以Ω為分岔參數，用PNF法[9-10]求解Ω0處的不動點X0及周期數P；

（2）用延續算法[15]以ΔΩ為步長，追蹤Ω=Ω0+ΔΩ處的周期解不動點X；

（3）求解不動點轉遷矩陣的最大Floquet乘子|λmax|，判斷其|λmax|是否大于1，若|λmax|≥1轉入步驟（4），否則轉入步驟（2）；

（4）當|λmax|≥1時，系統發生了分岔，該點為分岔點，并由Floquet理論[16]判斷分岔類型，停止該周期的延續追蹤，以下一點為新起始點，轉入步驟（1）重新求解周期和不動點；

（5）當遍歷Ω參數區域結束追蹤。

取α=0，Ω∈[1，2]的分岔圖和判穩圖如圖2所示。圖2Ⅰ分岔圖表明：在參數區間內系統主要以周期1（P1，下同）運動存在，僅在Ω∈（1.414，1.502）內以P2運動形式存在。圖2Ⅱ為|λmax|判穩圖，最大Floquet乘子|λmax|從Ω=2開始以P1延續追蹤，當Ω∈（1.414，1.502）時，P1運動失穩|λmax|>1，端點為分岔點。

考查其分岔點的Floquet乘子，并判別其分岔類型如表1所示。其Floquet乘子能準確地找出其分岔點和分岔類型，同時延續算法不需大量的瞬態求解，提高求解效率，故較Runge-Kutta法求解速度更快。

圖2 PNF延續法分岔及判穩圖

Fig.2 Bifurcation and stability diagram by PNF and continuation method

表1 基于PNF延續算法的系統分岔類型判別

Tab.1 Bifurcation type discriminant with PNF and continue method

考查點

（分岔點）參數 （Ω，α）追蹤周期PFloquet乘子λ|λmax|分岔類型A（1.414，0.0）P1（0.1844±0.8971i，0.9203，0.5614，-1.0228，-0.8207）1.0228倍化B（1.502，0.0）P1（0.6663 ± 0.3062i，-0.0246 ± 0.9193i，-1.0032，-0.8359）1.0032倍化C（1.263，0.5）P1（1.6521，0.4259，0.9053，0.9053，0.7125，0.7750）1.6521鞍結D（1.337，0.2）P2（0.6564 ± 0.7573i，-0.3892 ± 0.7315i，0.1072 ± 0.3943i）1.0022HopfE（1.376，0.2）P2（1.8340，0.5643，0.5643，0.8331，0.8331，0.3020）1.8340鞍結

Floquet理論無法判斷含間隙系統的擦切運動及擦切分岔現象，故在延續追蹤中需按式（5）判斷。圖2Ⅰ中頻率Ω的部分相圖如圖3所示。在分岔點A點前系統處于無沖擊單周期運動（圖3（a）），在分岔點A處不但發生了倍化分岔（圖3（b）），且系統位移穿越非光滑點x5=1（x=b）截面發生了擦切分岔，故在分岔圖上表現出了幅值跳躍現象。在Ω∈[1.570，1.590]區間內系統為穩定的P1運動，但系統經歷了單邊沖擊（圖3（c））、擦切運動（圖3（d））和無沖擊運動（圖3（e））的轉遷，因穿越x5=1截面時周期運動狀態未改變，故在Ω=1.580處僅發生了擦切運動。

圖3 相圖

Fig.3 Phase diagrams圖4 系統綜合非線性動態特性圖

Fig.4 Nonlinear dynamic characteristic graphs

3.2 頻率Ω對系統綜合動力特性影響

時變嚙合剛度幅值系數α是表征齒輪嚙合重合度大小，傳動穩定性的主要指標；無量綱頻率Ω是表征系統轉速高低的主要指標。因此，選取參數α和Ω為分析對象。

取無量綱頻率Ω為分岔參數，分別取α為0，0.2，0.5表示高、中和小重合度嚙合狀態，結合式（5），（6）和（8）計算出其系統動態傳動誤差x5隨Ω變化的分岔、沖擊、脫嚙、動載系數等非線性特性如圖4所示。

圖4（a）為α=0的時不變剛度系統，系統經歷了P1-P2-P1運動轉遷形成周期泡分岔，在Ω=1.414和1.502處發生了倍化分岔（如表1所示）。在Ω∈（1.414，1.580）區間系統發生了脫嚙單邊沖擊（impact=1，圖4（a）Ⅲ），其脫嚙占空比較小（DC1<0.22，圖4（a）Ⅱ），受倍周期分岔的影響（Ω=1.502處）脫嚙占空比發生了跳躍突變。無沖擊（impact=0）狀態下動載系數較小（1

圖4（b）為α=0.2的小幅值時變剛度系統，系統經Hopf、鞍結激變、倍化分岔獲得了P1-擬周期-P2-混沌-…-P4-P2-P1的運動狀態。單邊沖擊區域擴大為Ω∈（1.310，1.722），脫嚙現象加劇，脫嚙占空比增大到0.6左右，動載系數增大到2.2左右，且在倍化分岔點Ω=1.515附近出現了極值。

圖4（c）為α=0.5的大幅值時變剛度系統，系統經鞍結激變、Hopf、倍化分岔出現了P1-混沌-P2-混沌-P2-混沌-P1-混沌-P1的系統運動狀態。單邊沖擊繼續擴大到Ω∈（1.263，1.923），在Ω∈（1.250，1.317）區間出現了齒背嚙合雙邊沖擊（impact=2）和脫嚙單邊沖擊（impact=1）的交替狀態，最大DC1穩定在0.6附近，DLC穩定在2.2左右。

結合圖4三種嚙合剛度幅值系數α仿真結果表明：隨α的遞增系統的混沌、擬周期運動范圍擴大，齒輪嚙合單邊沖擊、脫嚙占空比和動載系數遞增，穩定周期運動的范圍減少。α為常數時，隨Ω變化系統的沖擊特性、脫嚙現象、動載系數隨系統的擬周期或混沌運動而加劇。

3.3 （Ω，α）雙參平面內綜合動力特性分析

在（Ω，α）雙參平面內研究系統的綜合動力特性及其耦合轉遷規律具有工程實際意義。圖5（a）～（d）為系統的沖擊/周期“I/P”、脫嚙占空比“DC1”、齒背嚙合比“DC2”和動載系數“DLC”動態特性偽彩圖。

圖5（a）偽彩圖中，用不同的顏色區分不同的“I/P”運動 [17]，其區域的邊界線即為分岔曲線。為突出短周期運動狀態，對于周期數P≥65的周期運動、擬周期運動和混沌運動均用“I/n”表示。當系統從狀態“0/P”向“1/P”狀態轉遷時，如周期運動未變則發生了擦切運動（G m），如周期運動發生了變化則產生了擦切分岔（G Bif）其交線為擦切曲線。當系統從“I/P”向“I/（2P）”轉遷時發生了倍化分岔（PD Bif），其交線為倍化分岔曲線。系統的Hopf分岔（PF Bif）、鞍結分岔（SN bif）和激變分岔（CIC）由Floquet乘子判斷。脫嚙占空比DC1（圖5（b）），齒背嚙合比DC2（圖5（c））和動載系數DLC（圖5（d））灰度圖中，對動力特性指標分級處理，并用不同的灰度值表示其脫嚙、齒背嚙合和動載系數程度。

圖5 （Ω，α）雙參平面內系統非線性動力學特性圖

Fig.5 Nonlinear dynamic characteristic in the （Ω，α） two-parameter plane

在中高速輕載（Ω，α）∈（[1，2]，[0，0.5]）的雙參平面內，系統表現出豐富的分岔/沖擊特性，如圖5（a）所示。平面內系統以P1運動為主，從Ω=1向Ω=1.4遞增時，因齒面擦切和系統分岔點重合故在系統分岔點處伴隨有擦切分岔而激變。隨α遞增系統出現了如下幾種分岔現象：系統通過擦切、倍化方式通向“1/2”，“1/4”運動狀態（α<0.0475）；系統通過擦切、Hopf、鞍結分岔方式通向混沌“1/n”運動（0.0475<α<0.1675）；系統通過鞍結、激變、擦切分岔方式進入混沌“1/n”運動（0.1675<α<0.5）。從Ω=2向Ω=1.4附近遞減時，系統從“0/1”通過擦切運動轉遷為“1/1”運動，后經倍化分岔通向混沌“1/n”運動狀態。特別在（Ω，α）∈（[1.8，2.0]，[0.25，0.5]）區域內系統出現了周期3經鞍結分岔轉遷為混沌，同時存在多處擦切激變分岔現象使“0/1”轉遷為“1/n”，“1/3”，“1/8”等運動狀態。在混沌區域內系統混沌狀態出現了單邊沖擊混沌向雙邊沖擊混沌轉遷的現象，即在混沌狀態下出現了內部吸引子激變（CIC）現象。沿α方向， “1/2”運動向混沌運動轉遷過程中出現了自相似的叉式分支分形結構。

圖5（b）的脫嚙占空比（DC1∈（0，1））灰度圖揭示了雙參耦合下齒輪脫嚙程度。結合圖5（a），“0”表示無脫嚙現象，出現在“0/1”運動區域；“0～0.1”表示出現了輕微脫嚙沖擊現象（00.6）。在各類分岔點處脫嚙占空比發生了突變跳躍現象。

圖5（c）的齒背接觸嚙合比（DC2∈（0，1））灰度圖揭示了齒輪傳動雙邊沖擊齒背嚙合的程度。結合圖5（a）沖擊/周期運動狀態，在雙邊沖擊混沌“2/n”運動區域內出現了齒背接觸輕微沖擊（0

圖5（d）為動載系數（DLC>1）灰度圖，結合圖5（a），“1～1.2”表示動載荷輕微波動（12.2）。

根據齒輪嚙合原理，重合度越大（α越小），齒輪傳動平穩性越好，動載荷波動越小。綜合分析圖5（a）～（d）中系統動力特性綜合指標可得：時變剛度幅值系數是影響系統動力學的主要因素之一，系統動力學特性隨幅值系數增大（重合度較小）而變差，系統的分岔和嚙合沖擊在線性共振頻率（Ω=1.3～1.5）附近變得十分復雜，系統動力參數達到極值，仿真結果和工程實際基本吻合。因此在齒輪系統參數設計中通過增大重合度減小剛度幅值系數和調整結構參數避開共振頻率是提高系統疲勞壽命的有效措施。在“0/1”區域內根據設備實際需要的動載系數選擇參數區域為齒輪結構設計提供理論依據。

4 結 論

在時變嚙合剛度幅值系數和無量綱頻率雙參平面內，用PNF延續算法對單級齒輪非線性系統進行數值求解獲得了分岔、嚙合沖擊、齒背嚙合、脫嚙、動載系數偽彩圖。通過分析獲得如下結論：

1）綜合運用PNF法和延續算法進行系統穩態周期解/分岔求解是一種高效、精確的數值方法。

2）時變嚙合剛度幅值系數是影響齒輪周期運動分岔、脫嚙、動載系數增大的主要因素之一。齒輪嚙合綜合特性隨嚙合剛度系數的增加（重合降低）而變差，直至系統混沌失穩，影響系統的疲勞壽命。

3）含間隙齒輪系統除了常見的倍化、Hopf、鞍結激變分岔外還存在擦切激變分岔，而分岔引起了系統動載系數、脫嚙現象的階躍突變。

4）系統共振頻率和齒側間隙所引起的分岔和嚙合沖擊是導致脫嚙、動載系數突變的主要因素，在混沌區域其沖擊和動載現象最劇烈達到極值。

5）在雙參平面內的無沖擊周期1運動“0/1”區域內選取動載系數參數是提高設備穩定性延長疲勞壽命的主要措施。

參考文獻：

[1] Kahraman A， Singh R. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration， 1990， 142（1）：49—75.

[2] Vinayak H， Singh R， Padmanabhan C. Linear dynamic analysis of multi-mesh transmissions containing external rigid gears [J]. Journal of Sound and Vibration， 1995，185（1）：1—32.

[3] 劉曉寧，王三民，沈允文. 三自由度齒輪傳動系統的非線性振動分析[J]. 機械科學與技術， 2004，23（10）：59—61.

LIU Xiaoning， Wang Sanmin， SHEN Yunwen. Nonlinear vibrations of 3-DOF geared rotor-bearing system[J]. Mechanical Science and Technology for Aerospace Engineering， 2004，23 （10）：59—61.

[4] 茍向鋒，陳代林.三自由度齒輪傳動系統的分岔與混沌研究[J].機械科學與技術，2014，33（2）：199—203.

Gou Xiangfeng， Chen Dailin. Research on bifurcation and chaos of 3-DOF gear transmission system[J]. Mechanical Science and Technology for Aerospace Engineering， 2014，33（2）：199—203.

[5] 王曉筍， 巫世晶，周旭輝，等. 含磨損故障的齒輪傳動系統非線性動力學特性[J]. 振動與沖擊， 2013，3（16）：37—43，69.

Wang Xiaosun， Wu Shijing， Zhou Xuhui， et al. Nonlinear dynamics analysis of gear transmission system with wear fault [J]. Journal of Vibration and Shock， 2013， 3（16）：37—43，69.

[6] Luo Yuegang， Ren Zhaohui， Ma Hui. Stability of periodic motion on the rotor-bearing system with coupling faults of crack and rub-impact [J]. Journal of Mechanical Science and Technology， 2007， 21：860—864.

[7] Han Qingkai. Periodic motions of a dual-disk rotor system with rub-impact at fixed limiter [J]. Proc. JMSE， Part C： Journal of Mechanical Engineering Science， 2008， 222（C10）： 1935—1946.

[8] Han Qingkai. Periodic motion stability of a dual-disk rotor system with rub-impact at fixed limiter [J]. Vibro-Impact Dynamics of Ocean System， LANCM， 2009，44：105—109.

[9] 李同杰，朱如鵬，鮑和云，等. 行星齒輪傳動系的周期運動及其穩定性[J].振動工程學報，2013，26（6）：815—822.

Li Tongjie， Zhu Rupeng， Bao Heyun， et al. coexisting periodic solutions and their stability of a nonlinear planetary gear train[J]. Journal of Vibration Engineering， 2013， 26（6）：815—822.

[10]楊 振，王三民，范葉森，等. 正交面齒輪傳動系統分岔特性[J]. 哈爾濱工業大學學報，2011，43（3）：107—110.

Yang Zhen， Wang Sanmin， Fan Yesen， Liu Haixia. Bifurcation characteristics of face-gear transmission system[J]. Journal of Harbin Institute of Technology， 2011，43（3）：107—110.

[11]田亞平，褚衍東，饒曉波. 單級齒輪系統的周期運動及其穩定性[J]. 機械設計，2017，34（2）：45—49.

Tian Yaping， Chu Yandong， Rao Xiaobo. Periodic motion and its stability of a single-stage gear system [J]. Journal of Machine Design， 2017， 34（2）：45—49.

[12]Gou Xiangfeng， Zhu Lingyun， Chen Dailin. Bifurcation and chaos analysis of spur gear pair in two-parameter plane [J]. Nonlinear Dynamic， 2015， 79：2225—2235.

[13]茍向鋒， 陳代林. 雙參變量下齒輪-轉子系統扭轉振動特性分析[J].工程力學，2014，31（11）：211—217.

Guo Xiangfeng， Chen Dailin. Dynamic analysis on torsional vibration of gear-rotor system in two parameters plane[J]. Engineering Mechanics， 2014，31（11）：211—217.

[14]李潤方， 王建軍. 齒輪系統動力學-振動、沖擊、噪聲[M]. 北京：科學出版社， 1997.

Li Runfang， Wang Jianjun. Gear System Dynamics Vibration， Shock and Noise[M]. Beijing： Science Press， 1997.

[15]胡海巖. 應用非線性動力學[M]. 北京：航空工業出版社，2000.

Hu Haiyan. Application of Nonlinear Dynamics[M]. Beijing： Aviation Industry Press， 2000.

[16]韓清凱，于 濤，王德友，等. 故障轉子系統的非線性振動分析與診斷方法[M]. 北京：科學出版社，2010.

Han Qingkai， Yu Tao， Wang Deyou， et al. The Nonlinear Rotor System Vibration AnalysIs and Fault Diagnosis Method[M]. Beijing： Science Press， 2010.

[17]Luo G W， Zhu X F， Shi Y Q. Dynamics of a two-degree-of freedom periodically-forced system with a rigid stop： diversity and evolution of periodic-impact motions[J]. Journal of Sound & Vibration， 2015，334：338—362.

Dynamic characteristic analysis of a single-stage spur gear system in

two-parameter plane

TIAN Ya-ping1， CHU Yan-dong1，2， RAO Xiao-bo1

（1.School of Mechatronic Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China；

2.Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province，

Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract： In order to reveal the coupling relationship among bifurcation， gear meshing impact， tooth separation， tooth back-side contact and dynamic load coefficient （DLC） of the nonlinear gear system， the pseudo color maps of the meshing impact and period， duty cycle of the mesh apart （DC1）， duty cycle of the tooth back-side contact （DC2） and DLC for a single stage gear system are obtained by Poincaré-Newton-Fouquet （PNF） and the continuation numerical calculation method in the time-varying meshing stiffness amplitude coefficient （TVMSA） and dimensionless frequency two parameters plane. Research shows that the TVMSA and resonance frequency are main factors for bifurcation， gear meshing impact and DLC of the gear system. With the increase of TVMSA， the system's periodic motion turns to chaos by the way of period-doubling， Hopf， crisis， grazing， saddle node bifurcation and the DC1， DC2 and DLC increase. Meanwhile， the chaos， quasi periodic motion and meshing impact phenomenon appear near the resonant frequency， in which the DC1， DLC reach the extreme values. The dynamic characteristics transitions laws can provide the theoretical reference for the optimization of the gear structure parameter.

Key words： nonlinear vibration； single-stage spur gear system； dynamic characteristics； PNF method； two-parameter plane