Z型折疊板內共振下非線性振動特性研究

郭翔鷹 張楊 張偉

摘要：Z型折疊板是一類復雜多體結構，在工程實際中應用廣泛。以大型的空間可展開結構為實際工程背景，考慮了Z型折疊板折疊過程中各部件的運動耦合關系，基于Reddy經典板理論和von-Karman幾何非線性應變位移關系，利用Hamilton原理建立了Z型折疊板的非線性動力學控制方程。利用有限元分析得到了Z型折疊板結構的模態函數，運用二階Galerkin截斷，得到了Z型折疊板二自由度的非線性常微分方程。考慮系統主參數共振-1∶2內共振的情況，通過攝動分析得到系統四維直角坐標形式的平均方程，最后利用數值模擬方法研究了橫向激勵對Z型折疊板非線性動力學特性的影響。

關鍵詞： 非線性動力學； Z型折疊板； 內共振； 數值模擬

中圖分類號： O322文獻標志碼： A文章編號： 1004-4523（2018）02-0183-15

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.001

引言

可展開（折疊）結構具有悠久的研究歷史和工程應用。折疊板結構是可展結構體系中最常用的一種，近年來在航空航天和建筑領域中得到了廣泛的應用。在折疊狀態下，結構體積較小，可用于運輸或存儲；在外力作用或系統內部驅動下，結構逐步展開，最終達到完全展開的工作狀態，然后鎖定為穩定狀態[1-2]。其中，Z型折疊板結構是此類折疊結構中最為經典的一種，在航空領域主要被應用于可變體飛行器機翼結構，而其中運動過程中由于變形引起的結構非線性動態特性問題是結構平穩運行的關鍵。

在Z型折疊板結構振動特性的研究方面，國內外學者進行了大量的研究，如：Lee等[3-4]分別利用有限元方法和高階板理論研究了復合材料折疊板的振動特性。Pal等[5-8]分別使用有限元方法，高階層合板理論研究了復合材料層合板折疊結構的自由振動特性。Topal等[9] 利用一階板理論建立了具有對稱折疊角度的復合材料折疊板的動力學模型，通過MFD方法進行頻率優化，數值分析得出層合板的長厚度比、夾角、板的長度以及邊界條件會影響到其頻率特性。Jian等[10]建立了有限元模型，用一種條狀網格劃分單元，模擬了折疊板的靜態特征和動力學特性分析。Liu等[11]對折疊板多體系統進行了動力學建模，并用數值方法研究了其動態特性。張偉等[12]建立了變角度Z型梁的動力學方程，計算了結構的固有頻率和振動模態，并通過數值仿真和實驗驗證。此外，Zhang等[13-14]研究了復合材料正交鋪設層合板結構在外激勵作用下的非線性振動問題，分析了系統不同參數下的振動響應。浙江大學的趙孟良和關富玲等[15-16]研究了空間可展結構在外載荷作用下的運動特性。

然而，Z型折疊結構屬于多體結構，在外激勵作用下將產生大幅的非線性耦合振動響應，這部分的研究成果目前還很有限。本文根據實際工程背景，研究了一類Z型折疊板結構在一定頻率的外激勵作用下發生1∶2內共振情況下的非線性動力學特性。

1動力學模型和方程〖2〗1.1動力學模型以大型的空間可展開結構為實際工程背景，建立如圖1所示的力學模型，所研究的Z型折疊板采用碳纖維復合材料層合板，折疊結構由三部分組成，靠近固定端的部分稱為內板，用Ω1表示，完成翻轉動作的稱為中間板，用Ω2表示，中間板外側部分為外板，用Ω3表示。圖中O1x1y1，O2x2y2，O3x3y3分別為內板、中間板、外板的局部坐標系，全局坐標系Oxy與局部坐標系O1x1y1重合，各個板表面受到的橫向簡諧激勵表示為P1，P2和P3，如圖1所示。

模型中，各個部分之間通過剛性鉸鏈相連接，通過內部的作動器和機械結構進行折疊與展開動作，機構在變形時，內板與固定端相連接，中間板在一定的角度范圍內轉動，外板始終與內板保持平行。

本文研究過程中，滿足以下條件：

1）Z型折疊板3塊板是等厚度，等寬度的；

2）Z型折疊板3塊板在外激勵作用下不會產生材料本身的破壞。

圖1Z型折疊板的動力學模型

Fig.1Mechanical model of the Z-type folding plates第2期郭翔鷹，等： Z型折疊板內共振下非線性振動特性研究振 動 工 程 學 報第31卷1.2動力學方程的建立

本文選取折疊板材料為正交鋪設的碳纖維復合材料層合板，不考慮剪切效應，因此（σz ）z=+ /-h2=0，（τxz）z=+/-h2=0，（τyz）z=+/-h2=0，其中h為層合板結構厚度。

材料的本構關系如下

σxx

σyy

τyz

τzx

τxy=1112000

2122000

004400

000550

000066εxx

εyy

γyz

γzx

γxy（1）

式中ij為轉換彈性常數，定義為ij=T-1QijT-1T（2）并且T-1=cos2θsin2θ0

sin2θ〖〗cos2θ0

00cos2θ-sin2θ（3）正交鋪設復合材料層合板的彈性模量Qij（i=1，2，4，5，6； j=1，2，4，5，6）可以表示為如下形式：Q11=Q22=E1-ν2，Q12=Q21=νE1-ν2，

Q44=Q55=Q66=E2（1+ν）（4）內力和彎矩的關系可表示為：Nxxi

Nyyi

Nzzi=∑Nk=1∫zk+1zkσxxi

σyyi

σzzidz （5）

Mxxi

Myyi

Mzzi=∑Nk=1∫zk+1zkσxxi

σyyi

σzzizdz（6）本文所研究的Z型可折疊結構在橫向外載荷的作用下會產生較大的變形，因此這里用von-Karman大變形理論進行分析，各個板的非線性應變表達式為εx

εy

γxy=ε0+zε1（7）式中ε0=u0ixi+12w0ixi2

v0iyi+12w0iyi2

v0ixi+u0iyi+w0ixiw0iyi（8）

ε1=-ω20ix2i

-ω20iy2i

-2ω20ixiyi （9）式中下標i表示第i個板（i=1，2，3）。

根據正交鋪設碳纖維增強復合材料的結構特點，可得到內力與應變關系為N

M=AB

BDε1

ε2 （10）式中剛度矩陣Aij， Bij， Dij， 用如下形式表示Aij，Bij，Dij=∫h2-h2ij1，z，z2dz（11）根據經典的層合板理論[17]，3塊板上任意一點在局部坐標系中的位移分別表示為以下形式：ui=u0i（xi，yi，zi，t）-ziw0ixi（12a）

vi=v0i（xi，yi，zi，t）-ziw0iyi（12b）

wi=w0i（xi，yi，zi，t），（i=1，2，3）（12c）式中u0i，v0i，w0i是在板Ωi中性層上任意一點在X， Y， Z方向的位移。

根據本文模型中所建立的坐標轉換關系，Z型折疊板結構在全局坐標系下的位移場可描述為：r1=R1u1

v1

w1 （13a）

r2 = r1 L1 cosw1′（L1 ）

v2

w2 + R2 u2

v2

w2 （13b）

r3 = r2 L2 cosw2′（L2 ）

v2

w2 （L2 ） + u3

v3

w3 （13c）式中Li為各個板的長度， Ri 為坐標轉換矩陣，形式如下R1=1

1

1 （14a）

R2=cosθ0-sinθ

0〖〗10

sinθ0cosθ （14b）將上述表達式（1）～（14）代入Hamilton原理中，整理展開后得到用廣義位移表示的Z型折疊板結構的非線性動力學方程如下。

內板的非線性動力學方程為：

A11（2u01x21+w01x12w01x21）+A12（2u01x21+

w01x12w01x21）+A66（v01x1+u01y1+w01x1w01y1）=

I02u01t2-I13w01t2x1（15a）

A12（2v01y21+w01y12w01y21）+A22（2v01y21+

w01y12w01y21）+A66（v01x1+u01y1+w01x1w01y1）=

I02v01t2-I1（3w01〖〗t2y1）（15b）

A11[2u01x21w01x1+u01x12w01x21+3〖〗2w01x122w01x21]+

A12[2u01x21w01x1+u01x12w01x21+32w01x122w01x21]+

A12[2v01y21w01y1+v01y12w01y21+32w01y122w01y21]+

A22[2v01y21w01y1+v01y12w01y21+32w01y122w01y21]-

（D11+D12）4w01x41-（D22+D12）4w01y41-

8D664ω01x21y21+A66[2v01x12ω01x1y1+2u01y12ω01x1y1+

4w01x1w01y12ω01x1y1+v201x1y1w01x1+2u01x1y1w01x1+ 2v01x21w01y1+2u01x1y1w01y1+2w01x21w01y12+

2w01y21w01x12]+P1=I02w01t2+I1（3u01t2x1+

3v01t2y1）-I2（3w01t2x1+3w01t2y1）（15c）

中間板的非線性動力學方程為：

A11（2u02x22+w02x22w02x22）+A12（2u02x22+

w02x22w02x22）+A66（v02x2+u02y2+w02x2w02y2）=

I0（sinkθ+coskθ）2u02t2+I0（sinkθ+

coskθ）（2w01（L1）tx1+）u02-I1（sinkθ+

coskθ）3w01t2x2-I1（sinkθ+coskθ）A12（2v02〖〗y22+

w02y22w02y22）+A22（2v02y22+w02y22w02y22）+A66（v02x2+

u02y2+w02x2w02y2）=I02v02t2-I1（3w02t2y2）（15d）

A12（2v02y22+w02y22w02y22）+A22（2v02y22+

w02y22w02y22）+A66（v02〖〗x2+u02y2+w02x2w02y2）=

I02v02t2-I1（3w02t2y2） （15e）

A11[2u02x22w02x2+u02x22w02x22+w02x222w02x22]+

A12[2u02x22w02x2+u02〖〗x22w02x22+

32w02x222w02x22]+A12[2v02y22w02y2+

v02y22w02y22+32w02y222w02y22]+A22[2v02y22w02y2+

v02y22w02y22+32w02y222w02y22]-（D11+

D12）4w02x42-（D22+D12）4w02y42-8D664ω02x22y22+

A66[2v02x22ω02x2y2+2u02y22ω02x2y2+

4w02x2w02y22ω02x2y2+v202x2y2w02〖〗x2+

2u02x2y2w02x2+2v02x22w02y2+2u02x2y2w02y2+

2w02x22w02y22+2w02y22w02x22]+P2=

-I02sinkθ2w02t2+I02coskθ（2w01（L1）tx1+

）w02+I1（sinkθ+coskθ）3u02t2x2+I1（sinkθ+

coskθ）（2w01（L1）tx1+）u02x2+I1+3w02t2y2-

I2（sinkθ+coskθ）4w02t2x22+I2（sinkθ+

coskθ）（2w01（L1）tx1+）w202x22-I24w02t2y22 （15f）

外板的非線性動力學方程為：

A11（2u03x23+w03x32w03x23）+A12（2u03x23+

w03〖〗x32w03x23）+A66（v03x3+u03y3+w03〖〗x3w03y3）=

I02u03t2-I13w03t2x3+（-θ）（15g）

A12（2v03y23+w03y32w03〖〗y23）+A22（2v03y23+

w03y32w03y23）+A66（v03x3+u03y3+w03x3w03y3）=

I02v03t2-I1（3w03t2y3）（15h）

A11[2u03x23w03x3+u03x32w03x23+32w03x322w03x23]+

A12[2u03x23w03x3+u03x32w03x23+32w03x322w03x23]+

A12[2v03y23w03y3+v03y32w03y23+32w03y322w03y23]+

A22[2v03y23w03y3+v03y32w03y23+32w03y322w03y23]-

（D11+D12）4w03x43-（D22+D12）4w03y43-D664ω03x23y23+

A66[2v03x32ω03x3y3+2u03y32ω03x3y3+

4w03x3w03y32ω03x3y3+v203x3y3w03x3+2u03x3y3w03x3+

2v03x23w03y3+2u03x3y3w03y3+2w03x23w03y32+

2w03y23w03x32]+P3=I02w03t2+I13u03t2x3+

I13u03t2y3-I24w03t2x23-I24w03t2y23（15i）

結構整體的邊界條件滿足如下等式：u1（0）=0，u1 x1 = L1 = u2 （0） = L1 （16a）

u2 x2 = L2 = u3 （0） = L1 + L2 cosθ（16b）

u3 x3 = L3 = L1 + L2 cosθ + L3 （16c）

w1（0）=0，w1（L1）=w2（0）=0（16d）

w3 （0） = w2 （L2 ） = L2 sinθ（16e）

w1′（0）=0，w2″（0）=0，w3（0）=0（16f）

w01 （0）y1 x1 = 0 = 0 （16g）

2w2（0）y22x1 = L1 = 2w3（0）y23x2 = L2 = 0（16h）

w01 （b）y1 x1 = 0 = 0（16i）

2w2（b）y22x1 = L1 = 2w3（b）y23x2 = L2 = 0（16j）

2w03 tx3 x3 = L3 = L1 + L2 cosθ + L3 （16k）

（A12+A22）[v0iyi+12（w0iyi）2]y=0，b=0 （16l）

2w02 tx2 x2 = L2 = L1 + L2 cosθ （16m）2有限元模態分析

上述所建立的動力學控制方程是偏微分方程，利用數學方法直接求解極為困難，因此本文將采用Galerkin離散將偏微分方程轉換到常微分方程后進行求解。對于單一結構模型，其模態函數通常是可以直接根據經驗公式假設的，但Z型折疊板結構為多體結構，很難確定折疊板在外激振力作用下結構的振動模態。因此首先通過ANSYS有限元方法，對Z型折疊板進行模態分析和諧響應分析，得到Z型折疊板結構的固有頻率和模態。通過研究結構模態振型，確定系統的模態函數形式。最后，將無量綱形式的Z型折疊板結構的非線性動力學控制方程通過Galerkin方法進行二階離散，得到可求解的常微分方程組。

2.1有限元模型

航空領域實際應用中，Z型折疊板結構在折疊展開運動過程中的角速度很小，且折疊角度在0～150°的范圍內，因此本文將板折疊過程分解，看作是不同折疊角度板結構的準靜態慢變過程，選取幾個特定折疊角度來建立Z型碳纖維復合材料層合板結構的力學模型。

本章研究中取折疊角度為60°，90°和120°作為典型參數值，進行對比分析和討論。

有限元模型統一采用四邊形板單元，如圖2所示；設置彈性模量為5×105 MPa，泊松比為0.3。Z型折疊板的有限元模型尺寸參數如表1所示。

圖2模型網格劃分示意圖

Fig.2Meshing of the Z-type folding plate wing of the three angles

表1Z型折疊板有限元模型的尺寸參數

Tab.1Geometric parameters of the finite element model for the Z-type folding wing

板長度/m厚度/m寬度/m內板20.012.1中間板10.012.1外板40.012.12.2模態分析

通過對建立的有限元模型施加初始條件，進行模態分析，得到Z型折疊板結構不同折疊角度下前5階固有頻率如表2所示。

表2不同折疊角度前5階固有頻率（單位：Hz）

Tab.2The first five order natural frequencies of different folding angles （Unit：Hz）

階數60°90°120°10.560180.617540.6944322.711402.358002.6580033.225903.319903.6326043.550903.731604.2836057.367306.220905.96140

下面列出Z型折疊板結構在60°，90°，120°的折疊角度下的模態振型圖，如圖3～5所示。

由有限元模態分析結果可以看出，不同折疊角度下的Z型折疊板結構前5階模態可表示為： 第1圖3折疊角度為60°時Z型折疊板前5階模態振型圖

Fig.3The first five order mode shapes of the Z-type folding angle 60°圖4折疊角度為90°時Z型折疊板前5階模態振型圖

Fig.4The first five order mode shapes of the Z-type folding angle 90°圖5折疊角度為120°時Z型折疊板前5階模態振型圖

Fig.5The first five order mode shapes of the Z-type folding angle 120°

階為彎曲振動，第2階為扭轉振動，第3階為彎曲振動，第4階為彎扭耦合振動，第5階為彎曲振動。通過以上分析可以發現，Z型折疊板結構的前5階振動模態的形式與懸臂板結構前5階振動模態的形式相似。

3Galerkin離散

由于結構在共振情況下會發生劇烈的大幅振動，容易產生失穩及結構整體破壞等。因此，對于結構在共振情況下動力學響應的研究是十分必要的。

在有限元分析結果中可以發現，Z型折疊板結構在折疊角度為60°時，第4階固有頻率幾乎是第5階固有頻率1/2，存在1∶2內共振的情況，因此，本文將對Z型折疊板結構在主參數共振-1∶2內共振的情況下的動力學特性進行深入分析。

根據上述的分析結果，可選取懸臂板結構的振動模態函數形式作為Z型折疊板在折疊角度為60°時的模態函數，利用Galerkin方法對方程（15）進行二階截斷，得到系統常微分形式的非線性動力學方程。在滿足位移邊界條件的前提下，選取3個方向的基本函數分別如下：

Ui（x，y，t） = u1 （t）sinx/2πLi cosπyb +

u2 （t）sin3x/2πLi cos2πyb（17a）

Vi （x，y，t） = v1 （t）cosx/2πLi sinπyb +

v2 （t）cos3x/2πLi sin2πyb（17b）

Wi（x，y，t）=w1（t）Xi1（x）Yi1（y）+

w2（t）Xi2（x）Yi2（y） （17c）

根據4階常微分方程的通解，可將方程（17c）中的Xij（x）和Yi1（y）取為Xij （x） = Ai1 coshki x-Ai2 coski x-

Ai3 βi1 sinhki x + Ai4 sinki x，

Yij （x） = Bi1 coshki x-Bi2 coski x-

Bi3 βi1 sinhki x + Bi4 sinki x（18）式中Xij（x）是沿x軸方向的固支-自由梁函數，Yij（y）為y軸方向的自由-自由梁函數，ki1和ki2為特征方程的根，并有如下關系coski1coshki1+1=0

coski2coshki2-1=0（19）將系統實際參數L1=2 m，L2=1 m，L3=4 m代入式（17）可求得X，Y方向的模態函數，將方程（18），（19）代入邊界條件求得模態參數Aij和Bij，得到Xij（x）和Yij（y）的函數表達式，如下：

X11 =-4.9×10 - 5coshk11 x +

2.1×10 - 5cosk11 x - 6.6×10 - 5β11 ·

sinhk11 x-sink11 x （20a）

X12 = 0.25coshk12 x + 27.3cosk12 x -

0.25β12 sinhk12 x - sink12 x（20b）

X21 = -1.4×10 - 6coshk21 x +

1.3×10 - 6cosk21 x - 2.5×10 - 7β21 ·

sinhk21 x-sink21 x（20c）

X22 = 1.2×10 - 4coshk22 x-1.4cosk22 x -

0.12β22 sinhk22 x-sink22 x（20d）

X31 = -1.5×10 - 4coshk31 x +

3.4×10 - 4cosk31 x - 3×10 - 4β31 ·

sinhk31 x-sink31 x（20e）

X32 =0.25coshk32 x + 27.3cosk32 x -

0.25β32 sinhk32 x - sink32 x （20f）

同時，將外激勵也進行離散，表示為

Pi=Fi1sin3πxlisinπyb+Fi2sinπxlisin3πyb （21）

用二階Galerkin方法離散方程（15），并將離散后的面內位移u0，v0用橫向位移w0表示，整理可得到Z型折疊板橫向振動的常微分運動控制方程：

內板方程：

11+μ111+21w11+α112w12+α113w311+α114w312+ α115w12w211+α116w11w212=f11cos（ξt）（22a）

12+μ212+α121w11+22w12+α123w311+α123w312+α125w12w211+α126w11w212=f12cos（ξt）（22b）

中間板方程：

21+μ321+α21121w21+α21222w21+α21321w22+α21422w22+21w21+α216w22+α217w21u21+

α218w21u22+α219w22u21+α2110w22u22+

（α2111/θ）w321+（α2112/θ）w322+α2113（sinθ+

cosθ）w22w221+α2114（sinθ+cosθ）w21w222=

f21cos（ξt） （22c）

22+μ422+α22121w21+α22222w21+α22321w22+α22422w22+α225w21+22w22+α227w21u21+

α228w21u22+α229w22u21+α2210w22u22+w321+（α2212/θ）w322+α2213（sinθ+cosθ）w22w221+

α2214（sinθ+cosθ）w21w222=f22cos（ξt） （22d）

外板方程：

31+μ531+21w31+（α311+F1cosΩt）ω31+

α312w32+α313w331+α314w332+α315w32w231+

α316w31w232=f31cos（ξt）（22e）

32+μ632+22w32+（α322+F2cosΩt）ω32+

α321w31+α323w331+α324w332+α325w32w231+

α326w31w232=f32cos（ξt）（22f）

式中折疊角θ為3塊板的運動方程的連接參數，體現了3塊板之間的耦合運動關系。

4攝動分析

對于較復雜的非線性常微分方程，很難求出其精確解，需要用近似解析的方法求其漸近解來替代精確解。攝動分析是近似解析的一種方法，包括直接攝動法、多尺度法以及KBM法等。

因此，本章基于系統主參數共振-1∶2內共振的共振關系，使用多尺度方法進行攝動分析。系統共振關系表示如下：21=14Ω2+εσ1， 22=Ω2+εσ2（23）式中1，2是相應線性系統的第1階、第2階固有頻率。σ1，σ2為系統的調諧參數，為了方便分析，令Ω=1。

經過計算得到系統的直角坐標下平均方程為：

內板平均方程：

11=-12u1x11-σ11x12-3α113x211x12- 3α113x312-2α116x12x213+x214（24a）

12=-12u1x12+σ11x11+3α113x11x212+x311+ 2α116x11x213+x214（24b）

13=-12u2x13-12σ12x14-32α124x213x14+x314-α125x14x211+x212（24c）

14=-12u2x14+12σ12x13+32α124x214x13+x313+α125x13x211+x212-14f12（24d）

中間板平均方程：

21=-12u3x21-σ11x22+14α212x21x24-x22x23- 3α214x22x221+x222-2α217x21x223+x224（25a）

22=-12u3x22+σ11x21-14α212x21x23-x22x24+ 3α214x21x221+x222+2α217x21x223+x224（25b）

23=-12u4x23-32α225x24x223+x224-

α226x24x221+x222-14σ2x4（25c）

24=-12u4x24+32α225x23x223+x224+

α226x23x221+x222+14σ2x3-14f22 （25d）

外板方程：

31=-12u5x31-σ1x32-3α313x231x32+x332-

2α316x32x233+x234+12f31x32（26a）

32=-12u5x32+σ1x31+3α313x31x232+x331+

2α316x31x233+x234+12f31x32（26b）

33=-12u6x33-12σ2x34-32α324x233x34+x334-α325x34x231+x232 （26c）

34=-12u6x34+12σ2x33+32α324x234x33+x333+α325x33x231+x232-12f32（26d）

5數值模擬

根據數值分析結果發現，Z型折疊板內板的振動幅值很小且多為周期性顫振[18]，考慮到本文篇幅的限制，不再詳述，主要討論Z型折疊機板在橫向激勵作用下中間板和外板的非線性振動特性。

5.1幅頻響應特性分析

通過數值求解系統的四維平均方程，利用matlab軟件繪制3塊板的幅頻響應曲線，選取外激勵幅值和系統阻尼系數為控制參數，研究參數對系統幅頻特性的影響。

首先，根據實際參數的取值范圍，經過無量綱處理后，選取參數為μ1=0.25，μ3=0.22，μ4=0.14， σ3=-0.015，σ4=-0.014，α214=0.31，α217=0.0002，α225=-0.108，α226=3.5，μ5=0.37，μ6=0.56，σ5=1.77，σ6=1.88，α313=2.49，α316=-3.27，α324=7.16，α325=6.81，α313=2.49。

將2塊板的初始條件均設為x10=1.44，x20=1.55，x30=1.35，x40=-1.799。令外激勵幅值fi （i=2，3）的值分別為50和100，研究結構幅頻響應曲線的變化。圖中藍色曲線和紅色曲線分別表示結構第4階模態和第5階模態的幅頻響應曲線，橫坐標為調頻參數σi （i=2，3），縱坐標為振動幅值ai （i=1，2）， a1， a2 分別表示第4階和第5階的振動幅值。

由圖6和7可知，隨著外激勵幅值的增加，幅頻

圖6不同外激勵幅值下的中間板Ω2幅頻響應曲線

Fig.6The frequency-response curves of the middle plate Ω2 to the external excitation amplitude f2

圖7不同外激勵幅值下的外板Ω3幅頻響應曲線

Fig.7The frequency-response curves of the outer plate Ω3 to the external excitation amplitude f3

響應曲線的形態發生了不規律變化。隨著調頻參數的增加，系統振幅除中間板第5階模態以外都呈現減小的趨勢，并且會出現多值現象和跳躍現象。

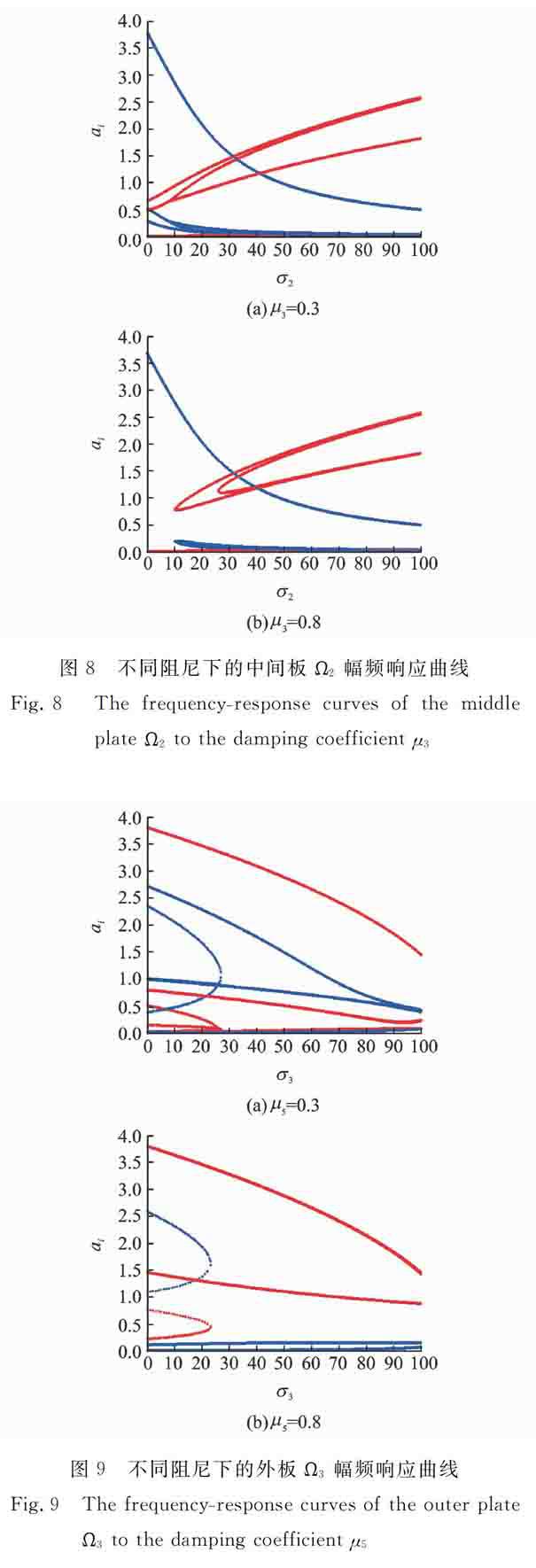
為研究系統阻尼系數對幅頻響應曲線的影響，分別令阻尼系數μi （i=3，5）的值為0.3和0.8。繪制如下幅頻響應曲線。

觀察圖8和9發現，隨著阻尼的增加，系統的振動幅值降低，幅頻響應曲線形態發生變化，且對第4階模態的頻響特性影響較大。隨著調頻參數σ的增加，系統會出現多值和跳躍的現象。

圖8不同阻尼下的中間板Ω2幅頻響應曲線

Fig.8The frequency-response curves of the middle plate Ω2 to the damping coefficient μ3

圖9不同阻尼下的外板Ω3幅頻響應曲線

Fig.9The frequency-response curves of the outer plate Ω3 to the damping coefficient μ5

5.2非線性振動響應分析

為了研究Z型折疊板系統在主參數共振-1∶2內共振的情況下的非線性振動響應特性，選取外激勵幅值fi為控制參數，研究橫向激勵幅值對系統產生周期運動和混沌運動的影響。

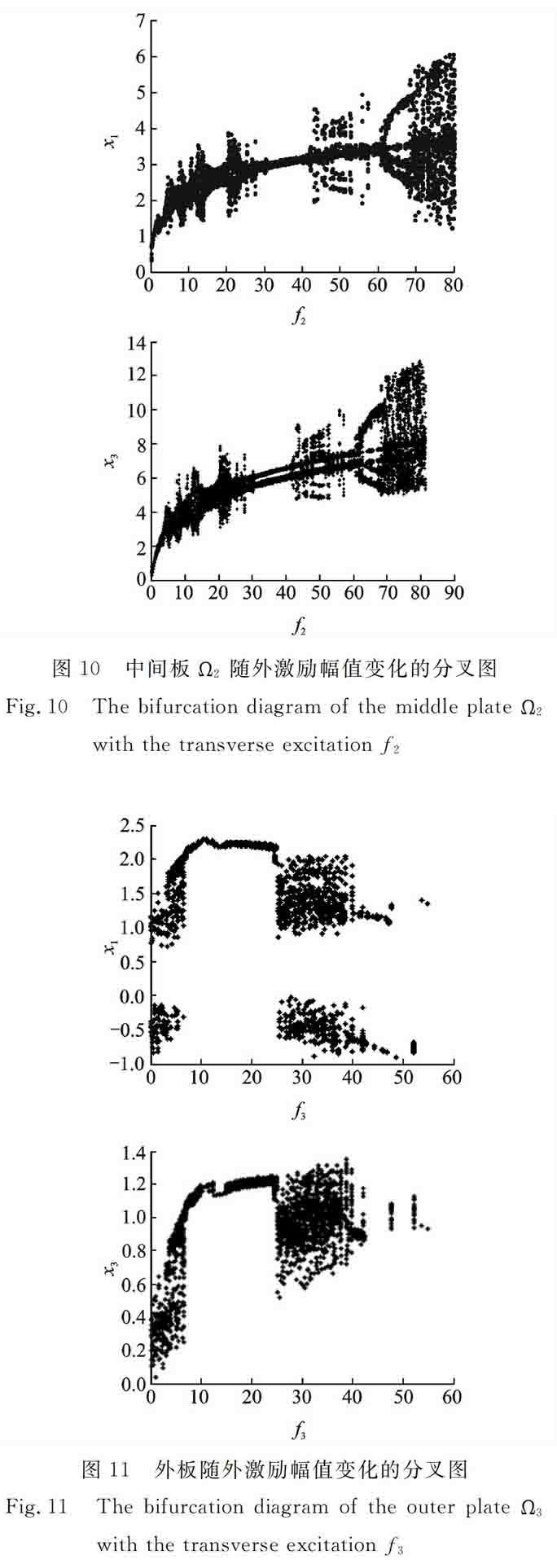
固定上述結構參數，改變外激勵的幅值，運用四階龍格庫塔法對系統運動方程進行數值求解，得到中間板和外板的混沌分叉圖，如圖10和11所示。

圖10中間板Ω2隨外激勵幅值變化的分叉圖

Fig.10The bifurcation diagram of the middle plate Ω2 with the transverse excitation f2

圖11外板隨外激勵幅值變化的分叉圖

Fig.11The bifurcation diagram of the outer plate Ω3 with the transverse excitation f3

由圖中可以看出，在外激勵幅值增大的過程中，結構會出現周期運動-混沌運動-周期運動-混沌運動的變化，說明共振情況下，外激勵幅值的變化對于系統的運動穩定性具有重要的影響。

為了更好地描述上述分叉圖的特性，首先對中間板隨外激勵幅值變化的振動特性給出了具體的分析：圖12，13和14分別給出了中間板在外激勵幅值為3，10和35時的波形圖、三維相圖和Poincaré截面，此時中間板的振動是從單倍周期進入短暫的混沌運動之后又變為倍周期運動。繼續增大外激勵幅值到，中間板的振動形式趨于復雜，逐漸變為如圖15所示的概周期運動，最后進入圖16所示的混沌運動，且不會伴隨外激勵幅值繼續增大而改變運動形態。

圖12f2=3時中間板的周期運動

Fig.12The periodic motion of the middle plate when f2=3圖13f2=10時中間板的混沌運動

Fig.13The chaotic motion of the middle plate when f2=10

外板隨外激勵幅值變化的振動特性如圖17～20所示。當外激勵幅值小于10時，外板呈現不規律的混沌運動，隨著外激勵幅值的增大，外板的振動形式趨于平穩，呈現周期運動形式；當外激勵幅值增大至25～38之間時，再次進入混沌運動，繼續增大外激勵幅值會發現外板再次變為規律的周期運動。圖17～20分別是外激勵幅值為3， 15， 35和45時外板的波形圖、三維相圖和Poincaré截面。圖14f2=35時中間板的4倍周期運動

Fig.14The period-4 motion of the middle plate when f2=35

圖15f2=65時中間板的概周期運動

Fig.15The quasi-period motion of the middle plate when f2=65圖16f2=80時中間板的混沌運動

Fig.16The chaotic motion of the middle plate when f2=80

圖17f3=3時外板的混沌運動

Fig.17The chaotic motion of the outer plate when f3=3圖18f3=15時外板的周期運動

Fig.18The periodic motion of the outer plate when f3=15

圖19f3=35時外板的混沌運動

Fig.19The chaotic motion of the outer plate when f3=35圖20f3=45時外板的周期運動

Fig.20The periodic motion of the outer plate when f3=45此外，中間板第5階模態的振動幅值比第4階模態的振動幅值大，外板第4，5階模態的振動幅值基本相差不大，這是由于系統在與第5階固有頻率對應的外激勵作用下，在這兩階模態存在1∶2的關系時發生了耦合的內共振現象。

6結論

本文利用Hamilton原理建立了在外激勵作用下Z型折疊板的幾何非線性動力學方程，并對系統在主參數共振-1∶2內共振情況下的非線性動力學行為進行了攝動分析，得到系統4自由度的平均方程。利用數值方法分析了系統的幅頻響應特性和混沌分叉特性。

數值結果表明，不同的外激勵幅值和阻尼系數會對系統的頻響特性產生一定的影響，且隨著調頻參數σ的增大，對應的系統振動幅值會出現多值和跳躍的現象。

選取一定的參數和初始條件，通過數值模擬發現，在主參數共振-1∶2內共振的共振關系下，當外激勵的頻率與系統第5階固有頻率相同時，只改變外激勵幅值時，中間板會出現單倍周期-混沌-概周期-混沌運動，外板會出現混沌-單倍周期-概周期-混沌運動，由此可見外激勵的改變會對系統的非線性動力學特性產生顯著的影響，且系統的第4階模態對應的幅值也會產生明顯的變化，說明此非線性系統的不同模態振動之間存在復雜的耦合關系。

因此，在研究Z型折疊板這一類結構的非線性動力學行為時，不應該只考慮單一的模態振動，還應考慮多階模態之間的相互作用，以便更好地利用或控制其運動形式，為實際工程提供重要的理論依據。

參考文獻：

[1]韓運龍. 折疊板殼結構的設計與分析[D]. 南京：東南大學， 2011：02.

Han Yunlong. Design and analysis of foldable plates structures[D]. Nanjing： Southeast University， 2011：02.

[2]陳務軍， 關富玲， 陳向陽. 可折疊航天結構展開動力學分析[J]. 計算力學學報， 1999，16：4.

Chen Wujun， Guan Fulin， Chen Xingyang. Dynamic analysis for deployment process of foldable aerospace structures[J]. Chinese Journal of Computational Mechanics， 1999， 16：4.

[3]Lee S Y， Wooh S C. Finite element vibration analysis of composite box structures using the high order plate theory[J]. Journal of Sound and Vibration， 2004，277（4-5）： 801—814.

[4]Lee S Y， Wooh S C， Yhim S S. Dynamic behavior of folded composite plates analyzed by the third order plate theory[J]. International Journal of Solids and Structures， 2004，41（7）：1879 —1892.

[5]Pal S， Gu H， Niyogi A. Application of folded plate formulation in analyzing stiffened laminated composite and sandwich folded plate vibration[J]. Journal of Reinforced Plastics and Composites， 2008，27（7）：693 —710.

[6]Haldar S， Sheikh A H. Free vibration analysis of isotropic and composite folded plates using a shear flexible element[J]. Finite Elements in Analysis and Design， 2005，42（3）：208—226.

[7]Hernández E， Hervella-Nieto L. Finite element approximation of free vibration of folded plates[J]. Computer Methods in Applied Mechanics and Engineering， 2009，198（15-16）：1360—1367.

[8]Peng L X， Kitipornchai S， Liew K M. Free vibration analysis of folded plate structures by the FSDT mesh-free method[J]. Computational Mechanics， 2006，39（6）：799—814.

[9]Topal U， Uzman . Frequency optimization of laminated folded composite plates[J]. Materials & Design， 2009，30（3）：494 —501.

[10]Jiang R J， Au F T K. A general finite strip for the static and dynamic analyses of folded plates[J]. Thin-Walled Structures， 2011，49（10）：1288—1294.

[11]Liu C， Tian Q， Hu H. Dynamics of a large scale rigid-flexible multibody system composed of composite laminated plates[J]. Multibody System Dynamics， 2011，26（3）：283—305.

[12]Zhang W， Hu W H， Cao D X， et al. Vibration frequencies and modes of a Z-shaped beam with variable folding angles[J]. Journal of Vibration and Acoustics， 2016，138（4）：041004.

[13]Guo X Y， Zhang W， Yao M H. Nonlinear dynamics of angle-ply composite laminated thin plate with third-order shear deformation[J]. Science China Technological Sciences， 2010，53（3）：612—622.

[14]Zhang W， Guo X Y， Lai S K. Research on periodic and chaotic oscillations of composite laminated plates with one-to-one internal resonance[J]. International Journal of Nonlinear Sciences and Numerical Simulation， 2009，10（11-12）：1567—1583.

[15]趙孟良， 關富玲， 吳開成. 空間可展板殼結構的展開分析[J]. 浙江大學學報（工學版）， 2006，40（11）：1837 —1841.

Zhao Mengliang， Guang Fulin， Wu Kaicheng. Deployment analysis of deployable space panel and shell structure[J]. Journal of Zhejiang University（Engineering Science）， 2006，40（11）：1837—1841.

[16]關富玲， 張惠峰， 韓克良. 二維可展板殼結構展開過程分析[J]. 工程設計學報， 2008，15（5）：351—356.

Guan Fuling， Zhang Huifeng， Han Keliang. Deployment analysis of two-dimensional deployable panel and shell structures[J]. Journal of Engineering Design， 2008，15（5）：351—356.

[17]Reddy J N. Mechanics of Laminated Composite Plates and Shells： Theory and Analysis[M]. CRC Press， 2004.

[18]樸金麗.Z 型折疊機翼的非線性動力學研究[D].北京：北京工業大學，2016：05.

Piao Jinli. Nonlinear vibrations for the Z-type folding wings of the morphing aircraft[D]. Beijing： Beijing University of Technology， 2016：05.

Nonlinear vibration characteristics of Z-type folding plates

with internal resonance

GUO Xiang-ying， ZHANG Yang， ZHANG Wei

（Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures，

Beijing University of Technology， Beijing 100124， China）

Abstract： The Z-type folding plate is a kind of complex multi-body structure， which is widely applied to many engineering fields. Based on the classical laminated plate theory and the von Karman type equation， the nonlinear dynamic equations of the Z-type folding plates are obtained by using the Hamilton′s principle. The mode functions of the Z-type folding plates are analyzed with the ANSYS. Then， the Galerk in procedure is used to obtain the normal differential governing equations of the nonlinear system. The case of primary parametric resonance 1∶2 inner resonance is considered. Based on the averaged equation obtained with the method of multiple scales， the numerical simulation is performed to indicate the nonlinear dynamical characteristics of the system.

Keywords： nonlinear dynamics； Z-type folding plates； inner resonance； numerical simulation