永磁同步電機改進模型預測電流控制

王鵬躍，王 英

（大連交通大學電氣信息工程學院，大連市116028）

1 引言

永磁同步電機（Permanent Magnet Synchronous Motor，PMSM）具有效率高、功率密度大、可靠性高等優勢，成為最近幾年研究較多的電機，并且在電動汽車、風力發電等諸多領域得到了廣泛應用［1-2］。永磁同步電機的傳統控制方法主要采用矢量控制和直接轉矩控制，但是傳統控制方法不能同時兼顧動態響應和穩定性。隨著半導體技術和計算機技術的發展，模型預測控制（Model Predictive Control，MPC）由于原理簡單，動態響應快，控制效果好的優點受到廣泛的關注和研究。

模型預測控制的控制思想是通過代價函數得到最優的開關狀態并將其直接應用逆變器，根據控制目標的不同，又可以分為電流預測控制［3-6］和轉矩預測控制［7-11］。采用電流預測控制時，代價函數只含有量綱一致的電流變量，設計簡單［12-13］。對于兩電平的逆變器，模型預測電流控制（Model Predictive Current Control，MPCC）需要進行 7次預測，然后進行比較選出使電流誤差最小的的電壓矢量，計算量大，不利于實際應用；控制器進行設計時，需對電機方程近似離散線性化處理，存在模型誤差，采用歐拉離散時要求采樣時間足夠小；數字實現時，采樣延時等因素會對控制性能產生影響。針對上述問題，本文采用工業上常用的雙線性變化對電機模型進行離散并對延時進行補償，從而提高系統穩定性。而后采用改進方法，判斷出期望電壓矢量所在扇區，再通過比較相關電壓矢量得到最優電壓矢量，從而減小計算量，最后通過仿真驗證了策略的有效性。

2 永磁同步電機數學模型

依據電機學原理，永磁同步電機在同步旋轉坐標系下的理想數學模型可以表示為：

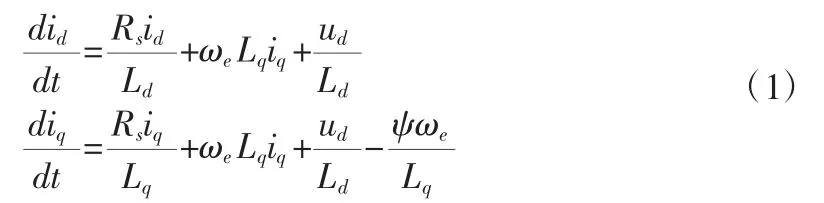
式中：ud、uq和id、iq分別為定子電壓矢量和電流矢量在 d-q軸上的分量；Rs為定子電阻；ωe為電角速度；ψ為轉子永磁體磁鏈；Ld、Lq為d-q軸電感，對于表貼式電機而言，有Ld＝Lq＝L。

3 傳統的MPCC算法

傳統MPCC采用歐拉法離散，式（1）離散后為：

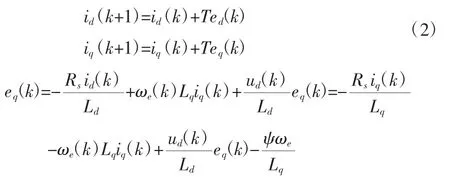
通過式（2）就能在第K個周期得到第K＋1周期的電流預測值。逆變器能夠輸出7種不同的電壓矢量，對應7組不同的ud（k）、uq（k），代入式（2）就會得到7組不同的的電流預測值，然后選出使代價函數最小的一組預測值，并將其對應的電壓矢量應用于逆變器。本文所選用的代價函數如下：

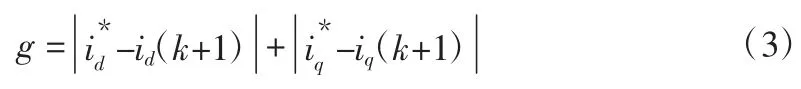
4 改進MPCC算法

4.1 離散化方法

雙線性變換法相當于數學中的梯形積分法，離散化公式為：

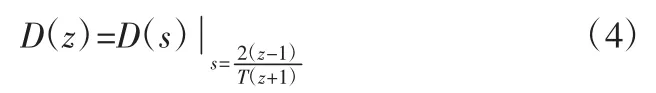
雙線性變換法的映射關系保證了若是D（s）穩定的，離散后D（z）也一定是穩定的，而傳統的歐拉離散化方法為：

這種離散方法不能保證D（z）一定是穩定的，若要保證穩定，則要求更小的采樣周期［13］。文獻［14］通過仿真得出了電機的極點分布圖，當離散時間減小后，電機在高轉速下的極點分布會有超出差分法穩定圓的情況，而電機極點始終分布在左平面中，始終滿足雙線性變換法的穩定性條件［13］，結果表明永磁同步電機調速系統采用雙線性法離散的穩定性更高。通過雙線性離散化公式對式（1）離散可得：

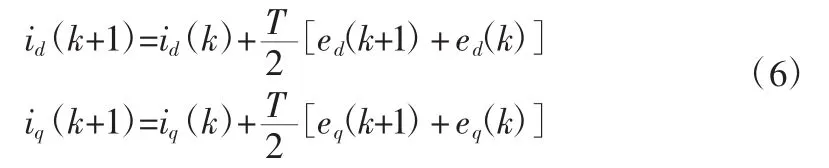
4.2 矢量選擇

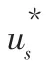
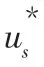
圖1 基本電壓矢量圖

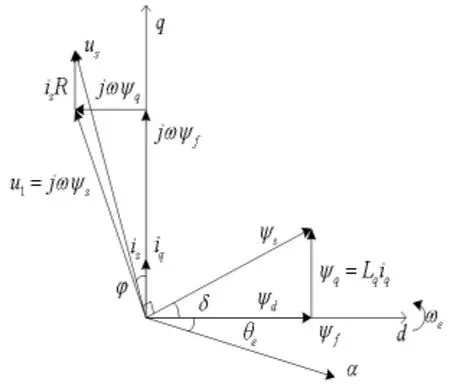
圖2 永磁電動機空間矢量圖

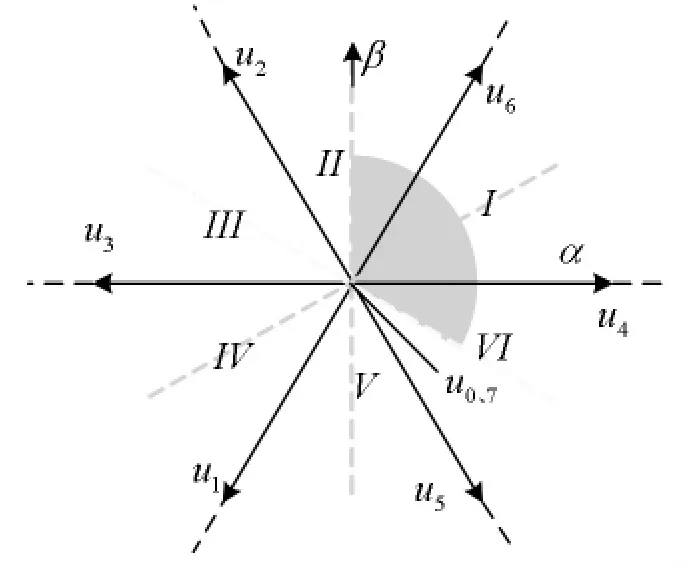
圖3 基本電壓矢量扇區劃分圖

4.3 延時補償

由于數字控制中存在采樣、計算延時等諸多延時因素，使得控制器的輸出存在滯后。即無法在KT時刻立即得出KT到（K＋1）T時刻應施加的控制狀態并應用，因此需要進行延時補償［17］。本文采用再進行一次預測的方式補償，由于采樣周期很短，近似認為KT到（K＋2）T時刻，電流的期望值i＊不變。在KT時刻采樣得到相關數據，先通過相關模型計算得到（K＋1）T時刻理論計算值i（k＋1），在此基礎上進行預測得到ij（k＋2），選出其中最接近i＊的ij（k＋2），并在下一采樣時刻應用對應的電壓矢量。

至此可以得到改進MPCC算法流程圖和控制結構圖，如圖4、圖5所示。

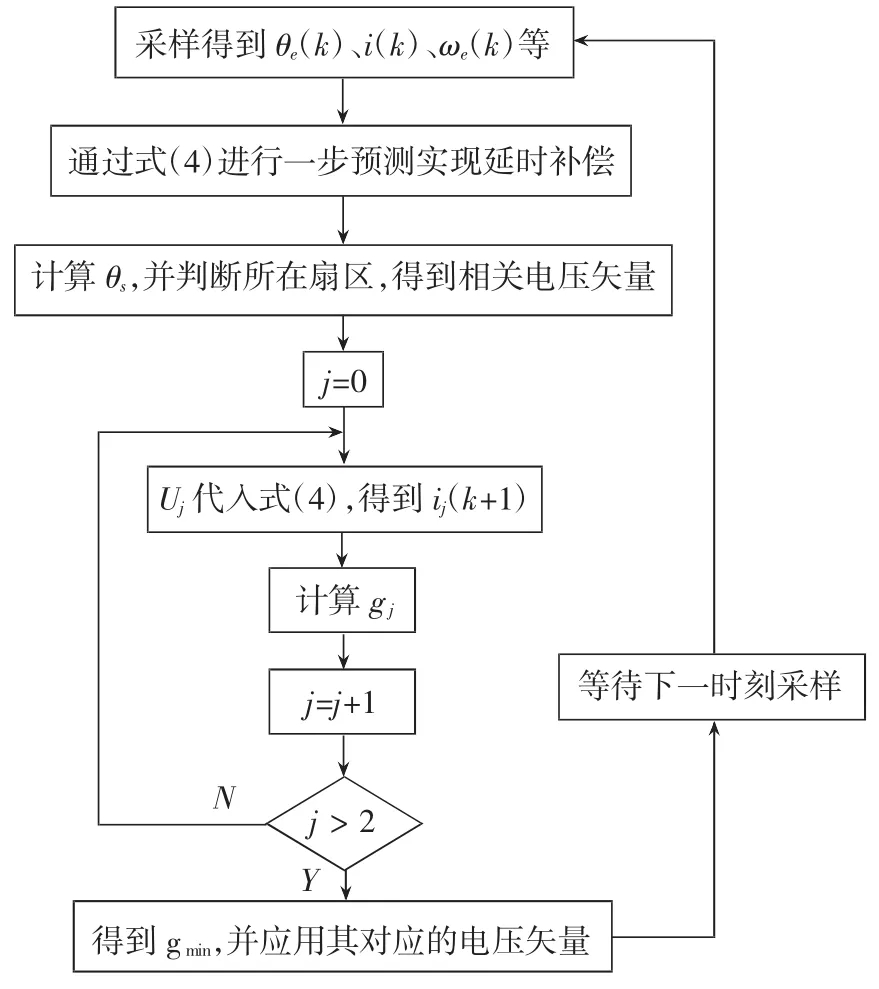
圖4 改進MPCC算法流程圖

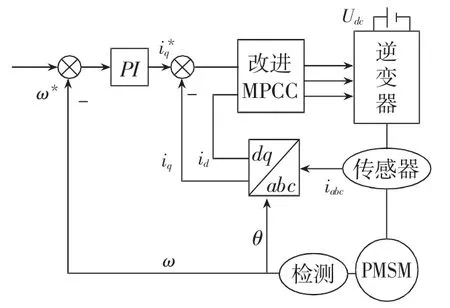
圖5 改進MPCC系統結構圖

5 仿真實驗

基于MATLAB/Simulink對所提控制策略進行仿真分析，通過文獻［18］建立速度環PI控制器，實驗電機參數：極對數 p＝4，Ld＝Lq＝0.0085H，定子電阻 R＝2.875Ω，永磁體磁鏈ψ＝0.175wb，J＝0.001kg·m2，B＝0.008N·m·s，給定轉速 1000r/m，Udc＝311V，采樣時間為 0.01ms，在 0.2s給予負載轉矩為 5N·m。

為驗證上文所提扇區劃分方法的有效性，分別對圖1的第一種扇區劃分和圖3所示的第二種劃分方式進行仿真，輸出轉矩如圖6所示。

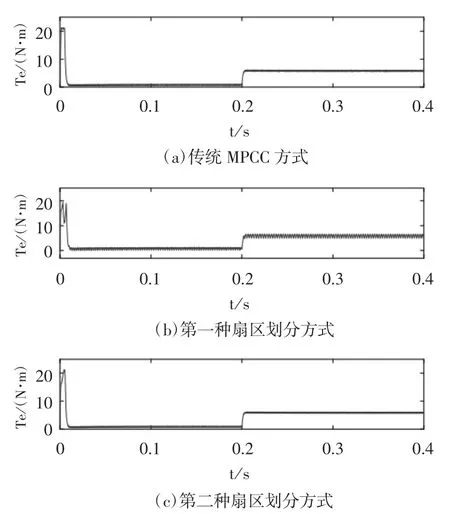
圖6 不同扇區劃分下MPCC輸出轉矩

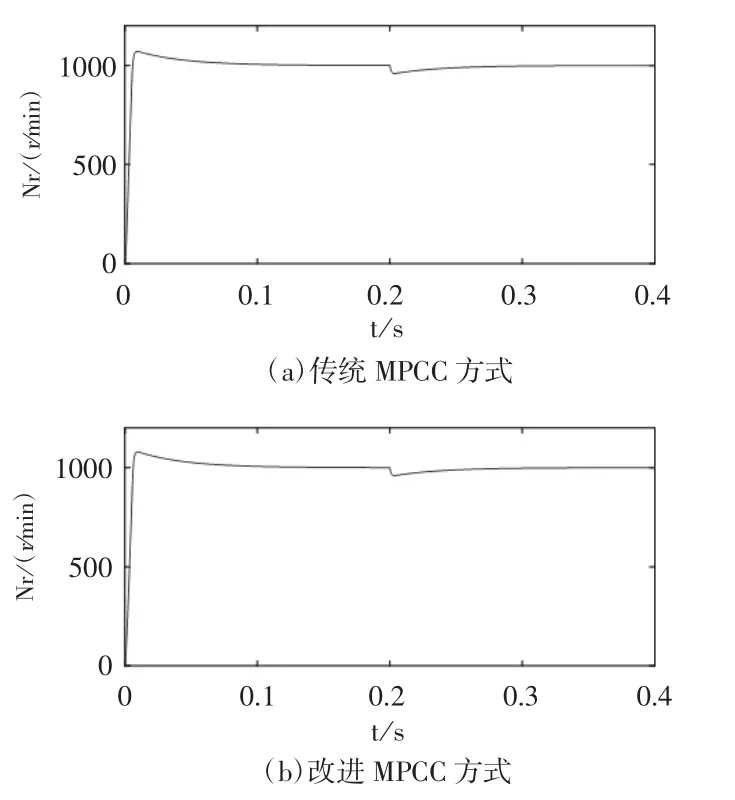
圖7 轉速波形

由圖6（b）可以看出，采用第一種扇區劃分方式時，空載和負載情況下轉矩脈動較大，并且加載后轉矩脈動增加。這是由于加載后q軸電流增加，忽略的電阻項增大了矢量選取的偏差。采用第二種劃分方式時，由于增加了一個判斷的電壓矢量，矢量最優范圍增加，抵消了電阻項的影響，與傳統MPCC方法相比，穩態下轉矩誤差（方差）相差0.0025，是可以接受的誤差范圍，證明這種方法并不會對轉矩穩態性能造成明顯影響。為提高控制精度，后文改進MPCC仿真采用第二種扇區劃分方式。

圖7給出的是兩種控制方式下的轉速波形。啟動時，改進MPCC方式的轉速超調量較傳統MPCC增加0.8%，但是其峰值時間更小，且兩種控制方式的調節時間相同。而后到仿真截止，兩者轉速波形基本重合，說明改進MPCC方法并未影響啟動后轉速環的性能。

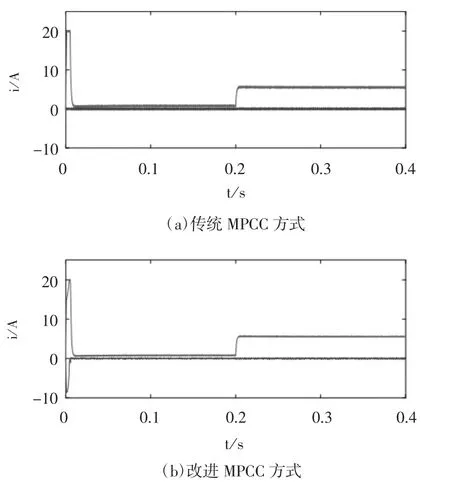
圖8 d-q軸電流波形

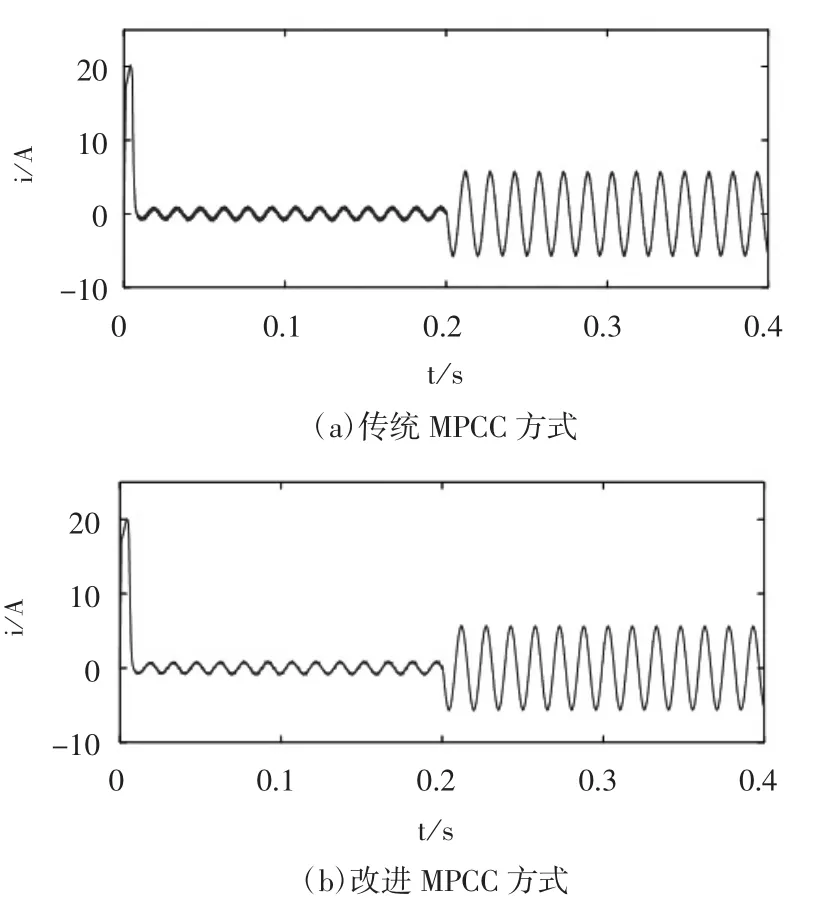
圖9 電機定子相電流波形

圖8為d-q軸電流波形，改進MPCC方式d軸在啟動階段出現了波動，但是能很快達到穩態，其調節時間以及加載后的動態響應速度與傳統MPCC方式相同，穩態時，改進MPCC的電流和轉矩誤差較傳統MPCC降低，相關數據如表1所示。

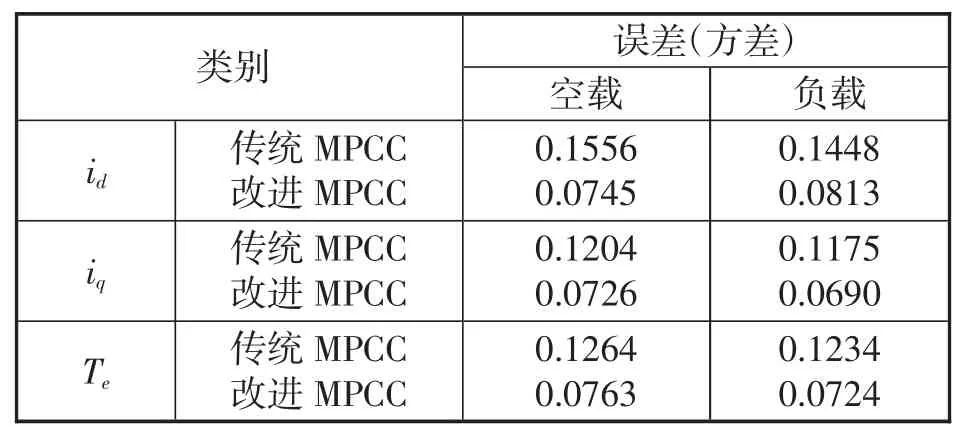
表1 不同控制方式的誤差

由于轉矩與q軸電流存在比例關系，在給出q軸電流波形的情況下，轉矩波形不再給出。

表2 帶載下定子電流畸變率

結合圖9和表2可以看出，改進方法電流波動明顯降低，定子電流畸變率更小，更接近正弦。由此可以證明改進MPCC方法的有效性。

6 結束語

本文采用雙線性變換法進行離散，并對延時進行補償，而后采用一種判斷期望電壓矢量所在扇區的方法，減小計算量。仿真結果表明，采用改進方法的定子電流畸變率更小，輸出轉矩脈動更小，具有更好的穩態性能。