激發(fā)聯(lián)想、學(xué)會(huì)構(gòu)造

郭小青

數(shù)學(xué)是一門(mén)創(chuàng)造性的藝術(shù)，蘊(yùn)含著豐富的美，而靈活、巧妙的構(gòu)造令人拍手叫絕，能為數(shù)學(xué)問(wèn)題的解決增添色彩，更具研究和欣賞價(jià)值。構(gòu)造法是一種極其富有技巧性和創(chuàng)造性的解題方法，體現(xiàn)了數(shù)學(xué)中發(fā)現(xiàn)、類(lèi)比、化歸的思想，滲透著猜想、探索、特殊化等重要的數(shù)學(xué)方法。美國(guó)著名數(shù)學(xué)教育家波利亞說(shuō)過(guò)，掌握數(shù)學(xué)就意味著要善于解題。運(yùn)用構(gòu)造法解數(shù)學(xué)題可激發(fā)學(xué)生的發(fā)散思維，利于培養(yǎng)學(xué)生思維的敏捷性、創(chuàng)造性和解題能力。下面通過(guò)幾個(gè)實(shí)例說(shuō)明構(gòu)造法的巧妙應(yīng)用。

引例：已知：a，b∈R+且a+b=1.求證：■+■≥■。

要證明上述問(wèn)題，方法很多，如比較法、分析法、綜合法，但是此題是一個(gè)無(wú)理不等式，直覺(jué)上是要先轉(zhuǎn)化為有理不等式，再通過(guò)平方后變形化簡(jiǎn)運(yùn)用基本不等式即可完成。但問(wèn)題是我們能否通過(guò)聯(lián)想、構(gòu)造法來(lái)解決這一問(wèn)題呢，如何構(gòu)造相對(duì)應(yīng)的數(shù)學(xué)模型呢？本文以下簡(jiǎn)述幾種常用的構(gòu)造方法。

一、依據(jù)幾何特征，聯(lián)想構(gòu)造平面幾何圖形

先仔細(xì)觀察此題結(jié)構(gòu)，聯(lián)想相應(yīng)的幾何背景，借助背景圖形的直覺(jué)功能，使較為抽象的數(shù)量關(guān)系轉(zhuǎn)化為更直觀的幾何圖形，以形助數(shù)，簡(jiǎn)單明了地抓住問(wèn)題的本質(zhì)。

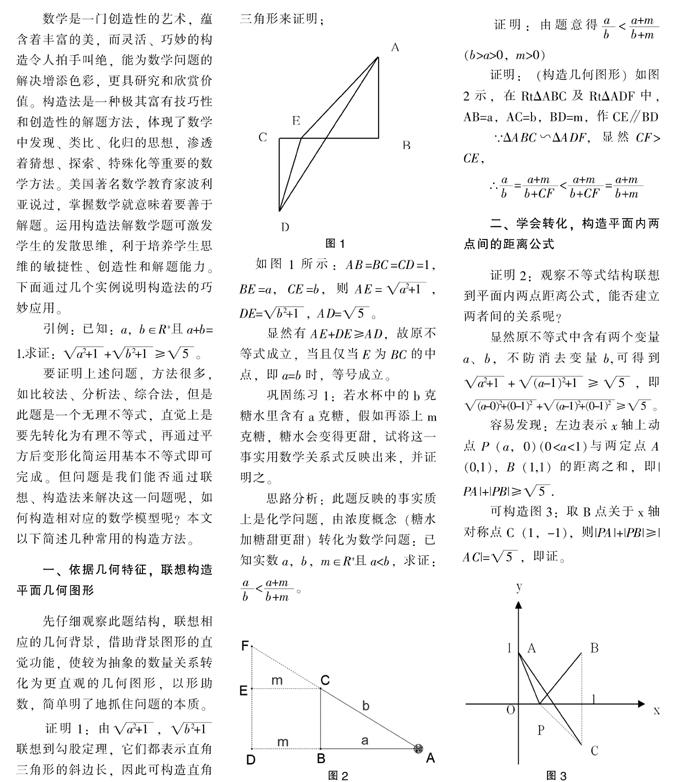
證明1：由■，■聯(lián)想到勾股定理，它們都表示直角三角形的斜邊長(zhǎng)，因此可構(gòu)造直角三角形來(lái)證明；

如圖1所示：AB=BC=CD=1，BE=a，CE=b，則AE=■，DE=■，AD=■。

顯然有AE+DE≥AD，故原不等式成立，當(dāng)且僅當(dāng)E為BC的中點(diǎn)，即a=b時(shí)，等號(hào)成立。

鞏固練習(xí)1：若水杯中的b克糖水里含有a克糖，假如再添上m克糖，糖水會(huì)變得更甜，試將這一事實(shí)用數(shù)學(xué)關(guān)系式反映出來(lái)，并證明之。

思路分析：此題反映的事實(shí)質(zhì)上是化學(xué)問(wèn)題，由濃度概念（糖水加糖甜更甜）轉(zhuǎn)化為數(shù)學(xué)問(wèn)題：已知實(shí)數(shù)a，b，m∈R+且a

證明：由題意得■<■（b>a>0，m>0）

證明：（構(gòu)造幾何圖形）如圖2示，在Rt？駐ABC及Rt？駐ADF中，AB=a，AC=b，BD=m，作CE∥BD

∵？駐ABC∽？駐ADF，顯然CF>CE，

∴■=■<■=■

二、學(xué)會(huì)轉(zhuǎn)化，構(gòu)造平面內(nèi)兩點(diǎn)間的距離公式

證明2：觀察不等式結(jié)構(gòu)聯(lián)想到平面內(nèi)兩點(diǎn)距離公式，能否建立兩者間的關(guān)系呢？

顯然原不等式中含有兩個(gè)變量a、b，不防消去變量b，可得到■+■≥■，即■+■≥■。

容易發(fā)現(xiàn)：左邊表示x軸上動(dòng)點(diǎn)P（a，0）（0

可構(gòu)造圖3：取B點(diǎn)關(guān)于x軸對(duì)稱(chēng)點(diǎn)C（1，-1），則|PA|+|PB|≥|AC|=■，即證。

證明3：通過(guò)均值代換構(gòu)造兩點(diǎn)距離公式；令a=■+m，b=■-m（-■

左邊=■+■=■+■.塔表示x軸上動(dòng)點(diǎn)Q（m，0）（-■

鞏固練習(xí)2：?jiǎn)柈?dāng)x取何值時(shí)，函數(shù)y=■+■有最小值，并求出最小值。

解析：

∵ y=■+■

=■+■

=■+■

注意到此時(shí)觀察式子結(jié)構(gòu)特點(diǎn)，從而聯(lián)想到平面兩點(diǎn)距離公式，

求y=■+■的最小值就是求軸x上的點(diǎn)到A、B兩點(diǎn)的距離之和的最小值。如圖4示：作點(diǎn)A（1，-2）關(guān)于x軸的對(duì)稱(chēng)點(diǎn)A'（1，2），根據(jù)平面幾何知識(shí)，A'B就是所求的最小值，易知：ymin=A'B=■=5。

設(shè)P的坐標(biāo)為（x，0），則由得■=■，得x=■，所以當(dāng)x=■時(shí)，ymin=5。

三、通過(guò)類(lèi)比聯(lián)想，直接構(gòu)造復(fù)數(shù)或向量的模

通過(guò)觀察結(jié)構(gòu)特征，發(fā)揮聯(lián)想，對(duì)已有的認(rèn)知結(jié)構(gòu)模式相類(lèi)比，從而探索問(wèn)題新的意義，突破思維定勢(shì)，構(gòu)造新的模型，達(dá)到優(yōu)化解題效果。

證明4：由■，■聯(lián)想到復(fù)數(shù)、向量的模及其三角定理。

可設(shè)Z1=a+i，Z2=b+i.則|Z1|=■，|Z2|=■，|Z1+Z2|=■=■，再根據(jù)復(fù)數(shù)模定理|Z1+Z2|≤|Z1|+|Z2|，即證■+■≥■。

四、分析關(guān)系特征，直接換元，構(gòu)造三角函數(shù)模型。

由關(guān)系式a+b=1直接聯(lián)想cos2θ+sin2θ=1，可采用三角代換，將不等式問(wèn)題轉(zhuǎn)化到三角函數(shù)問(wèn)題。

證明5：令a=cos2θ，b=sin2θ（0<θ<■），則有：

左邊=■+■=■+■

≥2■

=2■

∵ 0

∴ 左邊≥2■=2■=5，當(dāng)且僅當(dāng)θ=■時(shí)，即a=b時(shí)，等號(hào)成立。

五、激活想象，發(fā)散思維，作較深層次的背景探究，回歸構(gòu)建基本函數(shù)模型

本題表面上看是無(wú)理不等式的證明，并有兩個(gè)變量相互制約，常采用純不等式的方法去證明。但如何仔細(xì)挖掘此題的結(jié)構(gòu)特征，能否聯(lián)想到相關(guān)的函數(shù)模型，利用函數(shù)的圖像、性質(zhì)解決，是否更有效呢？

證明6：由■，■聯(lián)想到與函數(shù)f（x）=■有關(guān)，將問(wèn)題轉(zhuǎn)化到研究函數(shù)f（x）=■的性質(zhì)入手，容易得到函數(shù)f（x）=■的圖象是等軸雙曲線y2-x2=1的上一支，且在第一象限。

觀察圖像可發(fā)現(xiàn)f（x）=■在R上是凹函數(shù)。即滿(mǎn)足■≥f（■）。因此■≥f（■）=f（■）

∴ f（a）+f（b）≥2f（■）=■

此解法思路頗為新穎，知識(shí)性較綜合，具有較大的靈活性和技巧性。在運(yùn)用過(guò)程中，應(yīng)有目的、有意識(shí)地進(jìn)行函數(shù)模型構(gòu)造，始終“盯住”要證、要解的目標(biāo)。有利于訓(xùn)練學(xué)生的思維能力和想象能力。

由以上例題可看出構(gòu)造法可以使某些抽象的代數(shù)問(wèn)題直觀化、生動(dòng)化，能夠變抽象思維為形象思維，有助于把握數(shù)學(xué)問(wèn)題的本質(zhì)。構(gòu)造法其實(shí)質(zhì)就是通過(guò)對(duì)條件和結(jié)論的分析，構(gòu)造輔助元素，它可以是一個(gè)圖形、一個(gè)方程（組）、一個(gè)等式、一個(gè)函數(shù)、一個(gè)等價(jià)命題等，架起一座連接條件和結(jié)論的橋梁，從而使問(wèn)題迎刃而解，解題過(guò)程簡(jiǎn)捷明了。

由此可見(jiàn)，構(gòu)造法是多么的重要。但由于它異于常規(guī)的思維，因此掌握起來(lái)有一定難度。只要同學(xué)們平時(shí)多加強(qiáng)這方面的訓(xùn)練，在做題中要注意培養(yǎng)這種思想意識(shí)，開(kāi)拓自己的思維視野，不斷在實(shí)踐中摸索，去粗取精，相信會(huì)取得很好的效果。

責(zé)任編輯黃博彥