一種斜坡橋梁樁基礎(chǔ)自由段樁長確定方法

董 捷，楊 越，徐永明，宋緒國

(1.河北建筑工程學(xué)院 土木工程學(xué)院，河北 張家口 075000；2.中國鐵路設(shè)計(jì)集團(tuán)有限公司 地路院，天津 300142;3.中國鐵路設(shè)計(jì)集團(tuán)有限公司 城市軌道交通數(shù)字化建設(shè)與測評技術(shù)國家工程實(shí)驗(yàn)室，天津 300142)

我國是一個(gè)多山的國家，山地面積約占國土面積的三分之二，新建橋梁及隧道占高速鐵路、高速公路線路里程的比重逐年增長，造成越來越多的新建橋梁墩臺(tái)被迫設(shè)置于高陡斜坡上[1]。以新建北京至張家口城際鐵路為例，正線設(shè)計(jì)里程橋隧比重占66.5%；長沙至昆明客運(yùn)專線湖南段正線橋隧約占總設(shè)計(jì)里程的70%，其中僅長沙至玉屏段就設(shè)計(jì)有120余處橋梁樁基礎(chǔ)位于高陡斜坡上。對于一般的橋梁樁基礎(chǔ)設(shè)計(jì)而言，根據(jù)我國現(xiàn)行的鐵路橋梁設(shè)計(jì)規(guī)范，針對樁基礎(chǔ)頂部承受側(cè)向外力(橫向力和力矩)時(shí)所采用的樁身內(nèi)力計(jì)算方法，目前均采用樁側(cè)土體地基系數(shù)沿深度呈直線增長的假定進(jìn)行力學(xué)分析，并依據(jù)彈性地基梁模型計(jì)算樁身內(nèi)力[2]。一般情況下，在進(jìn)行樁身變位(側(cè)向位移和轉(zhuǎn)角)、樁身內(nèi)力(彎矩和剪力)和樁側(cè)土的應(yīng)力分析時(shí)，假定土體為彈性介質(zhì)，計(jì)算中不考慮樁與土之間的摩擦力[3]。需要指出的是，若樁基礎(chǔ)設(shè)置于斜坡上，按照傳統(tǒng)方法計(jì)算樁身內(nèi)力，須將樁埋入段以下一定深度范圍的樁基礎(chǔ)視為自有約束，即不考慮該范圍內(nèi)樁周土的側(cè)向約束作用，并將埋入斜坡內(nèi)視為自由約束段的樁基長度稱為自由段樁長。現(xiàn)階段，樁基內(nèi)力計(jì)算時(shí)自由段樁長大多通過人為假定，進(jìn)而將自由段樁長以下的樁體套用彈性地基梁模型進(jìn)行內(nèi)力計(jì)算。顯然，樁基礎(chǔ)自由段長度的取值將影響斜坡上樁基的設(shè)計(jì)，直接關(guān)系到斜坡橋梁設(shè)計(jì)的安全性和經(jīng)濟(jì)性。由于現(xiàn)有規(guī)范對斜坡樁基礎(chǔ)自由段樁長的取值未給出明確具體的建議[4]，橋梁設(shè)計(jì)人員大多憑借經(jīng)驗(yàn)或估算公式初步判定斜坡自由段樁長的取值[5]。

斜坡橋梁樁基自由段樁長的取值方法研究涉及到樁與周邊巖土體的相互作用問題，長期以來斜坡樁土相互作用也是國內(nèi)外相關(guān)學(xué)者重點(diǎn)關(guān)注的研究領(lǐng)域之一。Broms等學(xué)者圍繞斜坡樁土相互作用展開了長期的研究工作，重點(diǎn)在力學(xué)模型分析和數(shù)值計(jì)算上開展了深入分析。但由于設(shè)計(jì)習(xí)慣不同，針對我國斜坡樁基礎(chǔ)自由段樁長研究工作相對較少[6-8]。部分學(xué)者意識(shí)到斜坡對樁基礎(chǔ)的側(cè)向承載力存在一定的影響，并分析了斜坡對樁身彎矩、剪力及水平變形的作用效應(yīng)[9]。少數(shù)學(xué)者借鑒斜坡上抗滑樁錨固段樁長的計(jì)算方法[10]，建立了陡坡橋基自由段樁長的平面應(yīng)力分析模型[11]，遺憾的是，該計(jì)算模型未考慮樁前楔形滑動(dòng)體受到的重力和拉力。文獻(xiàn)[12]針對斜坡群樁基礎(chǔ)承受部分滑坡推力的狀態(tài)，建立了斜坡樁基礎(chǔ)的二維力學(xué)分析模型，并提出自由段樁長取值在承臺(tái)下方應(yīng)滿足不小于4倍樁徑。謝強(qiáng)等學(xué)者運(yùn)用數(shù)值仿真手段和橋基邊坡穩(wěn)定坡角線的假定分析其穩(wěn)定性，但研究成果主要圍繞橋基邊坡的整體穩(wěn)定性分析方法[13-14]，缺乏可用于確定斜坡樁基自由段長度的解析計(jì)算方法。

綜上所述，現(xiàn)有的分析方法大多將樁前無側(cè)向約束作用的楔形巖土體視為平面模型進(jìn)行計(jì)算，將一個(gè)三維問題簡化為二維模型進(jìn)行計(jì)算，或采用有限元開展三維數(shù)值仿真，而對此開展三維力學(xué)模型研究相對較少。另外，現(xiàn)階段設(shè)計(jì)人員擬定斜坡樁基的自由段樁長更多地側(cè)重于經(jīng)驗(yàn)和規(guī)律，自由段樁長取值的合理性和科學(xué)性得不到有效保障，在一定程度上影響了山區(qū)橋梁樁基礎(chǔ)工程設(shè)計(jì)的安全性和經(jīng)濟(jì)性。

本文針對斜坡橋梁樁基自由段樁長的取值問題展開研究工作，并應(yīng)用于長昆客運(yùn)專線橋梁樁基設(shè)計(jì)，以期為類似山區(qū)橋梁工程設(shè)計(jì)提供借鑒和幫助。

1 自由段樁長的確定方法

我國TB 10002.5—2005《鐵路橋涵地基和基礎(chǔ)設(shè)計(jì)規(guī)范》指出，當(dāng)樁基礎(chǔ)側(cè)面有斜坡時(shí)，若坡比小于1∶5，則地基系數(shù)的比例系數(shù)m可按照一半適當(dāng)進(jìn)行折減。遺憾的是，規(guī)范中對高陡邊坡上橋基地基系數(shù)的比例系數(shù)取值卻未作說明。對于高陡邊坡上的橋梁樁基而言，樁的受力往往極為復(fù)雜，目前仍缺乏充分的資料，造成對m取值難以做出統(tǒng)一規(guī)定。因此，高陡斜坡樁基礎(chǔ)的內(nèi)力計(jì)算變得尤為困難，設(shè)計(jì)人員被迫結(jié)合經(jīng)驗(yàn)人為擬定一個(gè)深度，忽略該深度范圍內(nèi)巖土體對樁基的側(cè)向約束，將該深度以下的樁基按照Winkler的半彈性空間假定進(jìn)行樁身內(nèi)力分析。

研究發(fā)現(xiàn)，斜坡樁基礎(chǔ)在承受一定橫向荷載時(shí)，樁前相鄰巖土體常沿某一潛在的滑動(dòng)面發(fā)生一定程度的錯(cuò)動(dòng)擠出變形。為簡化分析，一般將樁前發(fā)生側(cè)向擠出變形的受力體假定為五面楔形體ABFECD，這一受力體的底面在三維空間上可以簡化為一個(gè)平面，如圖1中的平面EFCD，該平面與樁基礎(chǔ)相交，交線EF以上至樁與坡面交線AB之間的垂直距離可視為受力體的深度y。圖1中：平面BFG和AEH為受力體ABFECD內(nèi)部的2個(gè)輔助面；b為樁基礎(chǔ)外邊界寬度；b1為受力體側(cè)向擴(kuò)展寬度；Bp為樁前楔形受力體換算寬度；λ為側(cè)向擠出拉裂面BFC與輔助面BFG以及拉裂面AED與輔助面AEH的夾角。

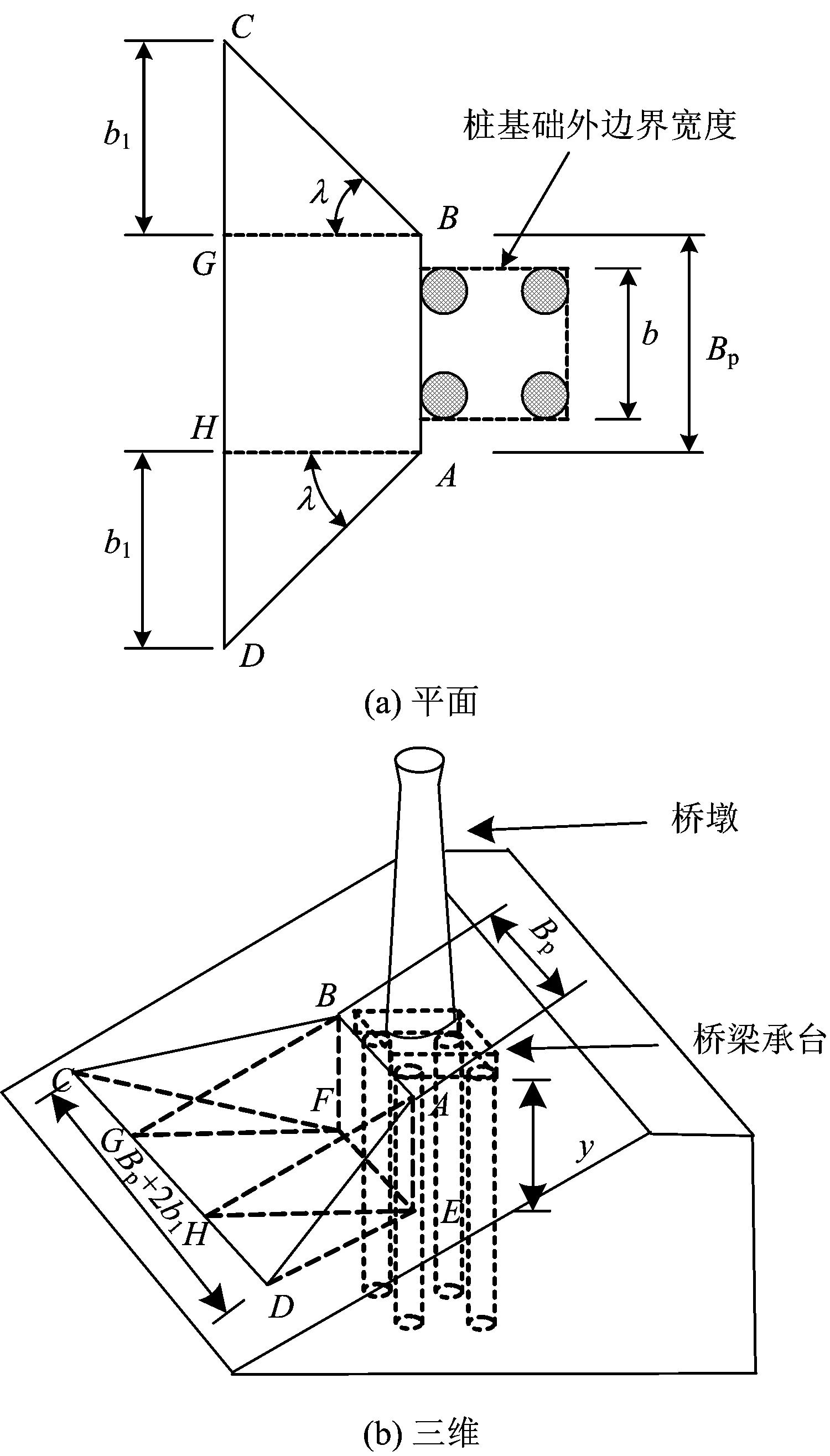
圖1 樁前楔形受力體與樁基相對位置關(guān)系

分析發(fā)現(xiàn)，若將樁基礎(chǔ)外邊界組成的矩形截面柱狀體視為一個(gè)整體的基樁進(jìn)行分析，該基樁承受一定橫向荷載，其與抗滑樁的受力模式頗為相似。部分學(xué)者將斜坡抗滑樁樁前楔形受力體視為平面應(yīng)力模型，并作二維簡化處理，得到了塑性區(qū)臨界高度。借鑒DB 50/5029—2004《地質(zhì)災(zāi)害防治工程設(shè)計(jì)規(guī)范》，依據(jù)抗滑樁樁前受力體底面EFCD上方巖土體的臨界靜力平衡條件，當(dāng)斜坡坡角為α，考慮其臨界破壞條件推導(dǎo)出樁前受力體臨界深度，按照斜坡抗滑樁自由段樁長計(jì)算方法，所對應(yīng)的抗滑樁自由段樁長ycr為

(1)

其中，

式中：σh為樁土接觸壓應(yīng)力；c為樁前楔形受力體的黏聚力；φ為樁前楔形受力體的內(nèi)摩擦角；Bp為樁前楔形受力體換算寬度[9]，一般取1.2b～2b；β為受力體底面EFCD與水平面之間的夾角，β=45°-φ/2；ω為角度換算參數(shù)；α為斜坡坡度。

不難發(fā)現(xiàn)，傳統(tǒng)抗滑樁自由段樁長ycr計(jì)算直接應(yīng)用于鐵路陡坡橋梁樁基自由段樁長ypcr的計(jì)算仍存在一些需要改進(jìn)的地方。與抗滑樁相比，橋梁樁基結(jié)構(gòu)的設(shè)計(jì)標(biāo)準(zhǔn)更高，為更接近實(shí)際情況，需要考慮樁前楔形受力體的重力，并考慮楔形受力體兩側(cè)拉裂面AED和BCF上受到的極限拉力。

鑒于此，考慮上述因素對斜坡樁基礎(chǔ)前方的楔形受力體進(jìn)行穩(wěn)定性分析，其主要承受重力W、接觸面的法向支撐力N、受力體底面EFCD上作用的極限摩阻力Ff、橫向樁土接觸壓力Fh和楔形受力體兩側(cè)受到的巖土拉力的合力FT作用，樁前楔形受力體剖面受力示意圖如圖2所示。

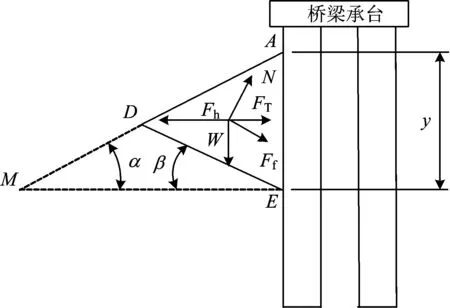
圖2 樁前楔形受力體示意圖

將斜坡樁前一定深度范圍內(nèi)的楔形受力體作為穩(wěn)定性分析對象，假定受力體的高度為y，依據(jù)空間幾何關(guān)系，可得楔形受力體側(cè)向擴(kuò)展寬度b1為

(2)

與ABEF垂直的輔助面AHE的面積為

(3)

樁前受力體的體積為

(4)

樁前受力體受到的重力為

(5)

式中：γ為樁前受力體的巖土重度。

受力體底面EFCD上的最大黏結(jié)力為

(6)

樁前受力體受到的橫向樁土接觸壓力為

Fh=σhby

(7)

樁前受力體兩側(cè)拉裂面上受到的極限拉力的合力為

FT=2σtS△AHE

(8)

式中：σt為樁前受力體拉裂面的抗拉強(qiáng)度。

樁前受力體底面EFCD受到的極限摩阻力為

Ff=(Wcosβ+Fhsinβ-FTsinβ)tanφ+Fc

(9)

則沿平行于受力體底面EFCD方向的受力體滑動(dòng)力合力為

FR=(Fh-FT)cosβ-Wsinβ-Ff

(10)

分析發(fā)現(xiàn)，當(dāng)受力體深度y較小時(shí)，往往受力體沿其底面EFCD的滑動(dòng)力合力FR>0，表明深度y范圍的受力體因滑移失穩(wěn)將發(fā)生側(cè)向擠出變形或松動(dòng)，該深度范圍內(nèi)受力體對樁基起不到側(cè)向約束作用。若逐漸增加樁前受力體深度y值，受力體滑動(dòng)力合力將逐漸變小，當(dāng)其滑動(dòng)力合力FR=0時(shí)，此時(shí)樁前受力體的穩(wěn)定性處于臨界狀態(tài)，其對應(yīng)的受力體深度y值即可視為樁基自由段樁長ypcr。

為便于計(jì)算，可令受力體深度計(jì)算的初始值y0取一較小值，增量ε一般取0.01，并令y=y0，代入式(10)計(jì)算FR。判斷得到的FR是否小于0，若不滿足條件，則繼續(xù)增加受力體深度y的計(jì)算值，令y=y+ε，直到滿足FR<0時(shí)，記錄下此時(shí)對應(yīng)的受力體深度y值，該值即可視為斜坡樁基礎(chǔ)自由段的樁長ypcr。計(jì)算步驟如圖3所示。

圖3 陡坡橋梁樁基自由段樁長計(jì)算步驟

為便于計(jì)算，本文采用C#語言，基于上述樁基自由段樁長的理論計(jì)算方法，開發(fā)了斜坡橋梁樁基自由段樁長的計(jì)算程序，圖4給出了該程序界面。

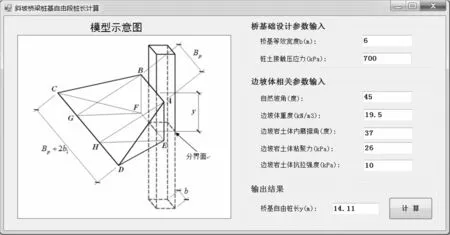
圖4 斜坡樁基自由段樁長計(jì)算程序界面

2 自由段樁長影響參數(shù)敏感性分析

可見，本文建立的斜坡橋梁樁基自由段樁長計(jì)算方法考慮了樁周巖土體強(qiáng)度、樁前楔形滑動(dòng)體兩側(cè)的抗拉強(qiáng)度、基礎(chǔ)換算寬度和楔形受力體自重等因素，為進(jìn)一步研究上述影響因素變化對樁基自由段樁長取值的影響，運(yùn)用上述方法，僅變動(dòng)某影響因素參數(shù)值，而其余影響因素的參數(shù)值保持不變，進(jìn)行上述影響因素的敏感性分析。

敏感性分析的基本參數(shù)設(shè)置如下：β=45°-φ/2，λ=45°，Bp=2b，斜坡坡角α=40°，巖土內(nèi)摩擦角φ=30°，巖土黏聚力c=40 kPa，巖土體重度γ=18 kN·m-3，樁周巖土體抗拉強(qiáng)度σt=10 kPa，樁基等效寬度b=4 m，樁土接觸應(yīng)力σh=500 kPa。

圖5為其他條件不變，不同坡角α條件下受力體滑動(dòng)力合力FR隨受力體深度y的變化曲線。由圖5可見：隨著斜坡坡角逐漸增加，樁前楔形受力體深度一定時(shí)，其所受的滑動(dòng)力合力逐漸增加。

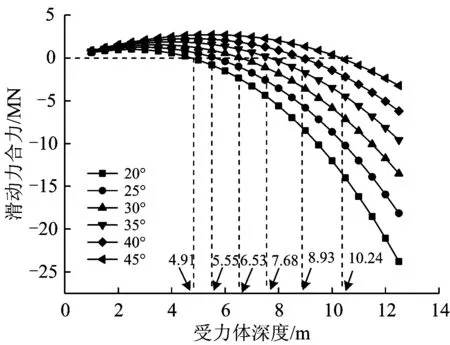
圖5 不同斜坡坡角、不同受力體深度的滑動(dòng)力合力

依據(jù)圖5，得到的不同斜坡坡角條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段樁長ypcr見表1，相應(yīng)曲線如圖6所示。

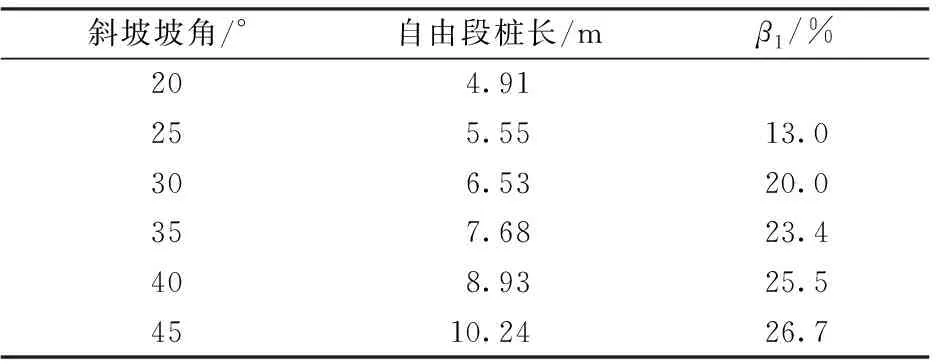
表1 不同斜坡坡角對應(yīng)的橋梁樁基自由段樁長

注：β1為斜坡坡角每增長5°自由段樁長的增長百分比。

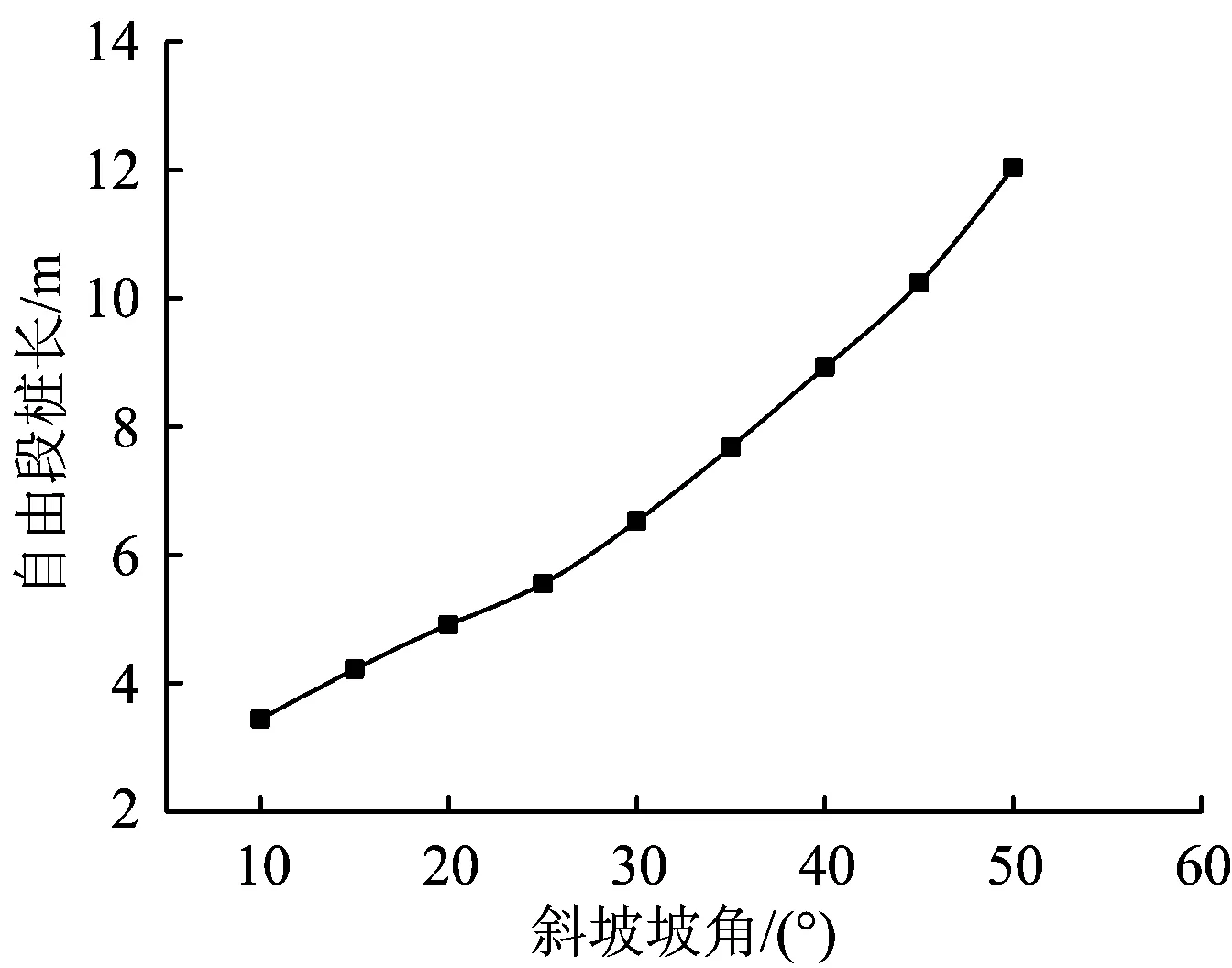
圖6 不同斜坡坡角時(shí)橋梁樁基的自由段樁長

由表1可知：斜坡坡角每增長5°時(shí)，對應(yīng)的自由段樁長分別增加13.0%，20.0%，23.4%，25.5%和26.7%。

由圖6可見：隨著斜坡坡角的增加樁基自由段樁長增大，且隨著邊坡逐漸變陡，自由段樁長逐漸增加的趨勢更為顯著。

圖7為其他條件不變，不同巖土體重度γ條件下受力體滑動(dòng)力合力FR隨其深度y的變化曲線。由圖7可見：隨著巖土體重度逐漸增加，樁前楔形受力體深度一定時(shí)，其所受到的滑動(dòng)力合力逐漸減小。

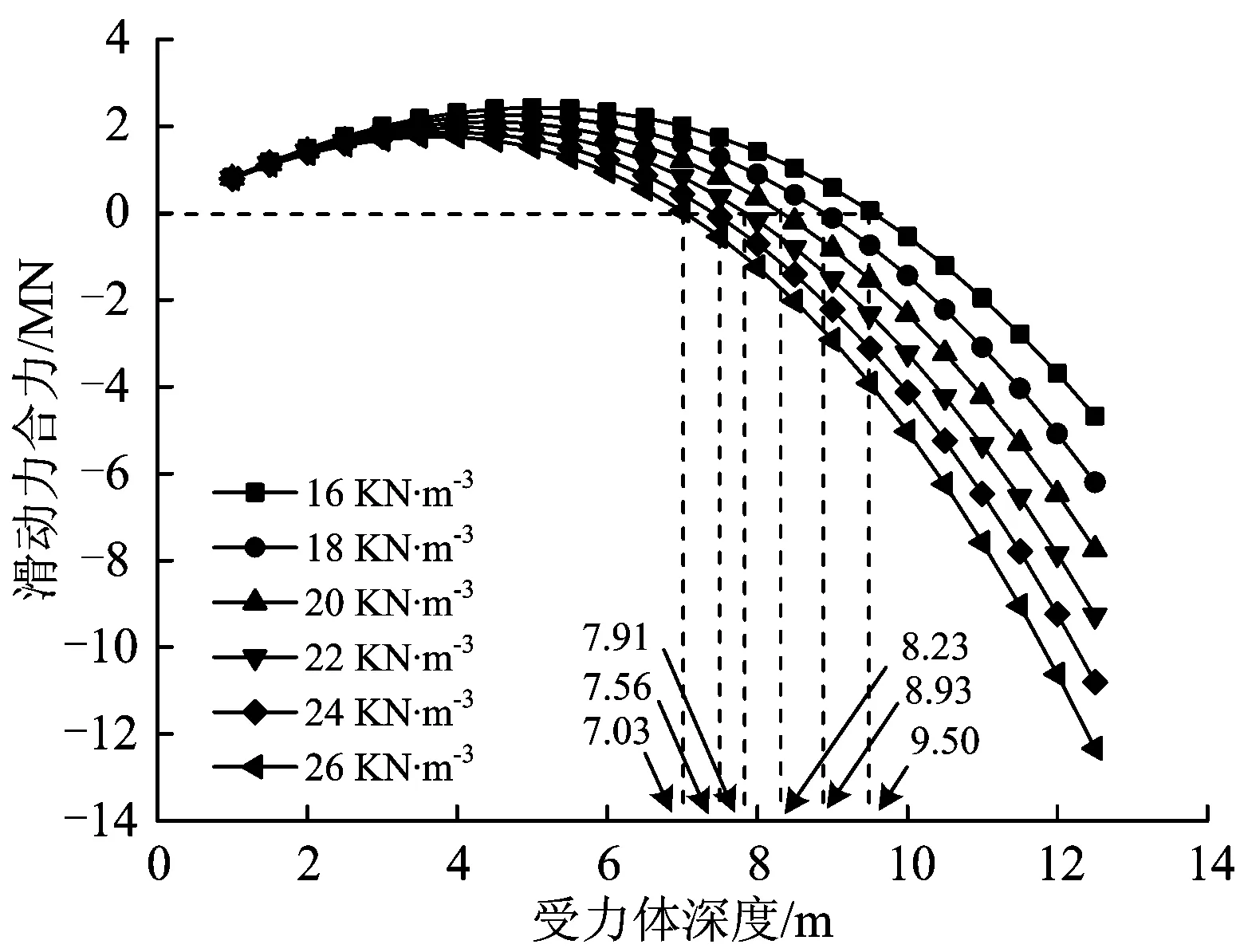
圖7 不同重度、不同受力體深度的滑動(dòng)力合力

依據(jù)圖7，得到不同巖土體重度條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段長度ypcr見表2，相應(yīng)曲線如圖8所示。

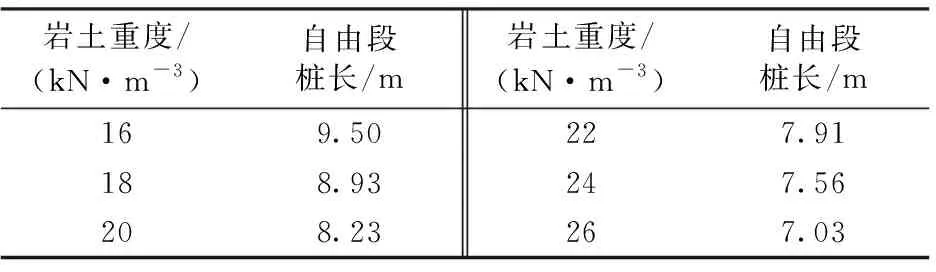
表2 不同巖土重度對應(yīng)的自由段樁長

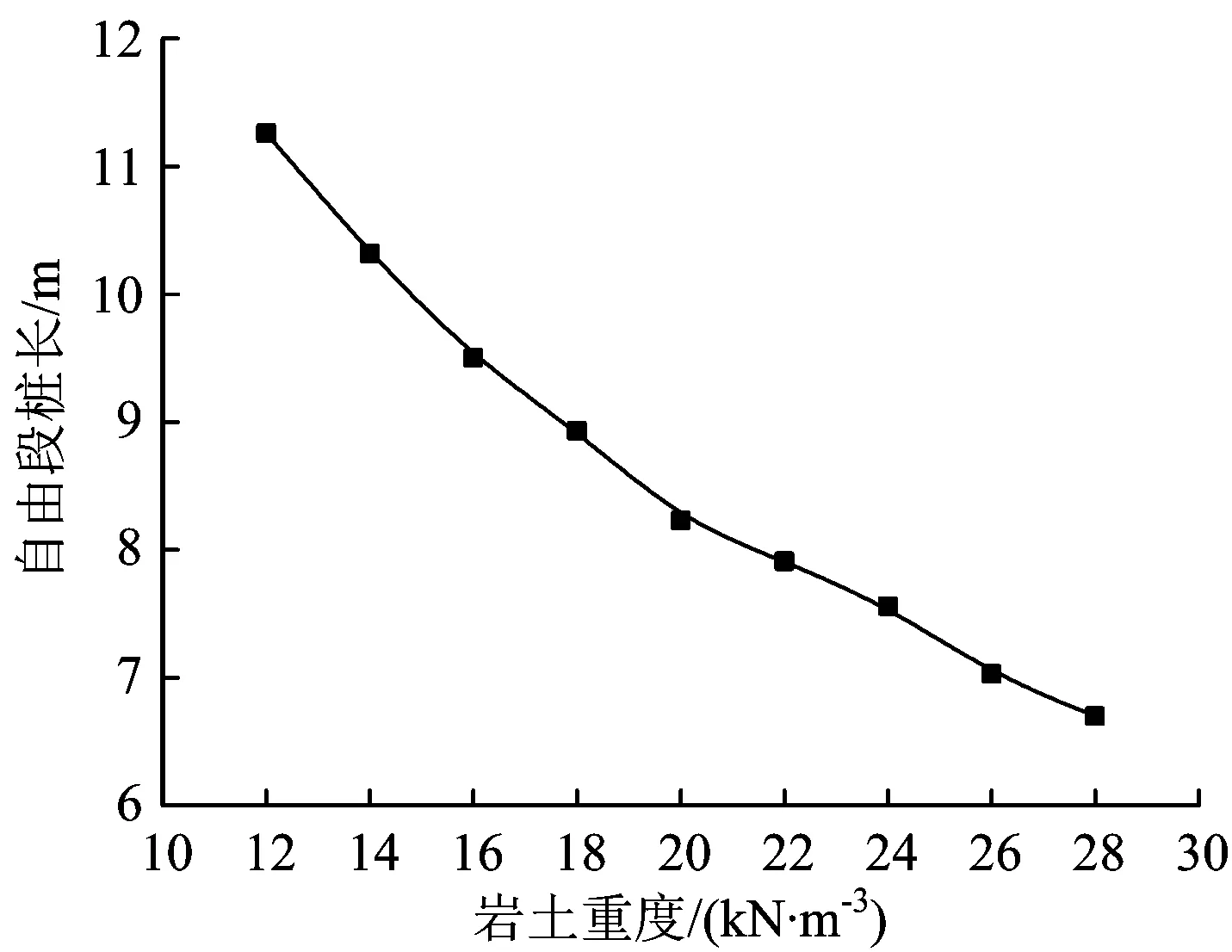
圖8 不同巖土重度時(shí)橋梁樁基的自由段樁長

由表2可知：巖土體重度每增加2 kN·m-3時(shí)，對應(yīng)的自由段樁長分別減小6.0%，7.4%，3.4%，3.7%和5.6%。由圖8可見：隨著巖土體重度的增加樁基自由段樁長逐漸減小。計(jì)算結(jié)果表明，樁周巖土體重度對自由段樁長的取值有一定的影響，若樁基礎(chǔ)自由段樁長計(jì)算依據(jù)現(xiàn)有抗滑樁樁前巖土體二維穩(wěn)定性計(jì)算方法，不僅計(jì)算模型被過度簡化，且忽略了樁前楔形受力體的自重，產(chǎn)生的誤差也相對較大[10]。

圖9為其他條件不變，不同內(nèi)摩擦角φ條件下受力體滑動(dòng)力合力FR隨受力體深度y的變化曲線。由圖9可見：隨著內(nèi)摩擦角逐漸增加，樁前楔形受力體深度一定時(shí)，其所受的滑動(dòng)力合力逐漸減小。

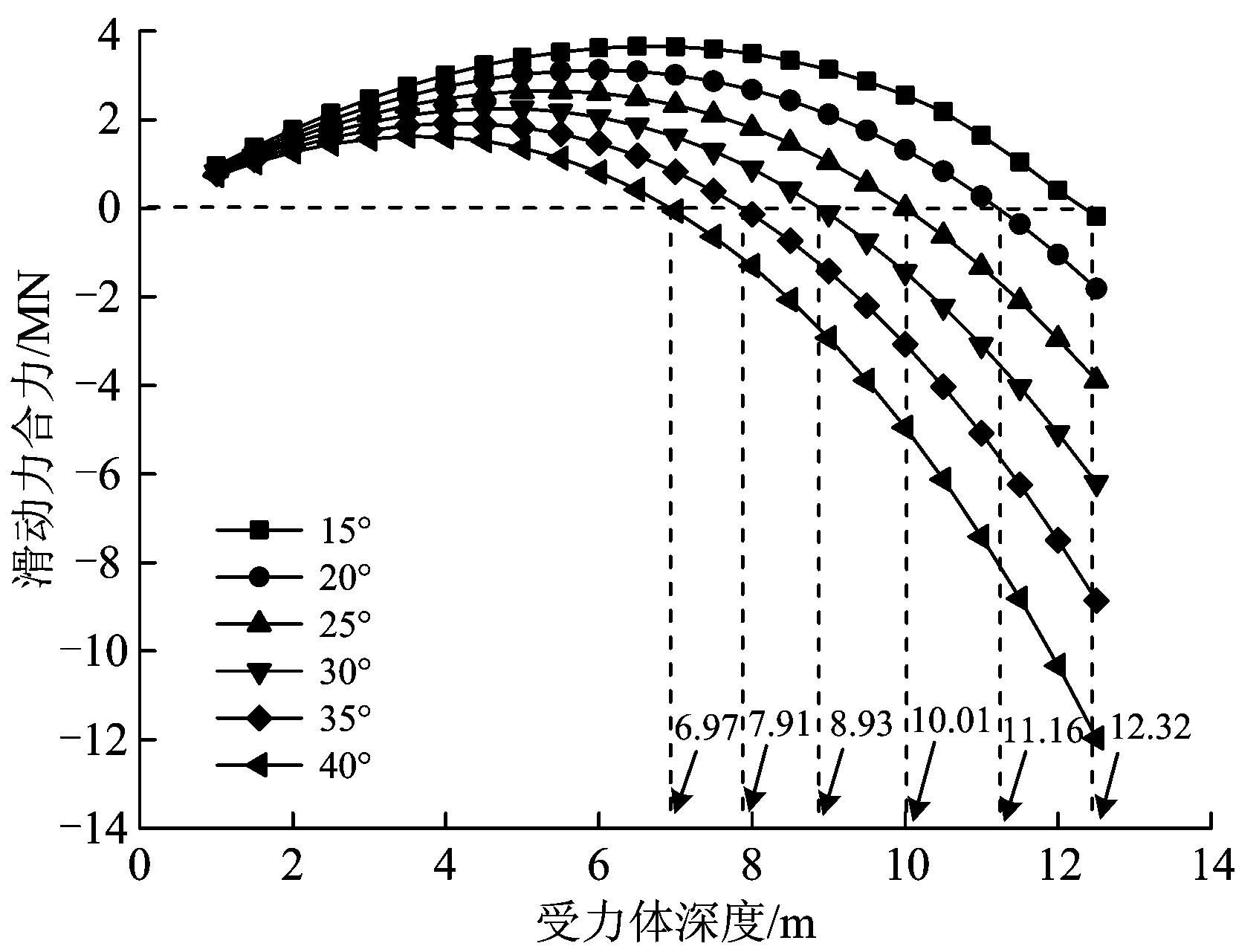
圖9 不同內(nèi)摩擦角、不同受力體深度的滑動(dòng)力合力

依據(jù)圖9，得到的不同內(nèi)摩擦角條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段樁長ypcr見表3，相應(yīng)曲線如圖10所示。

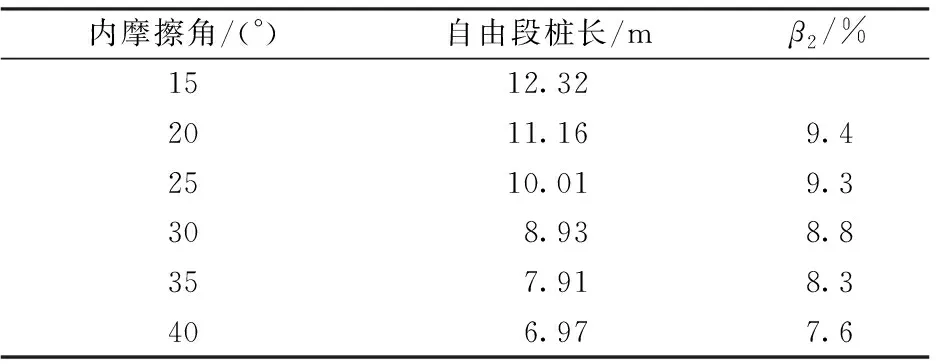
表3 不同斜坡坡角對應(yīng)的自由段樁長

注：β2為內(nèi)摩擦角每增長5°自由段樁長的減小百分比。

圖10 不同內(nèi)摩擦角時(shí)橋梁樁基的自由段樁長

由表3可知：內(nèi)摩擦角每增加5°時(shí)，對應(yīng)的自由段樁長分別減小9.4%，9.3%，8.8%，8.3%和7.6%。

由圖10可見：隨著內(nèi)摩擦角的增加樁基自由段樁長減小，且隨著內(nèi)摩擦角增加，自由段樁長逐漸減小的速率逐漸放緩。

圖11為其他條件不變，不同黏聚力c條件下受力體滑動(dòng)力合力FR隨受力體深度y的變化曲線。

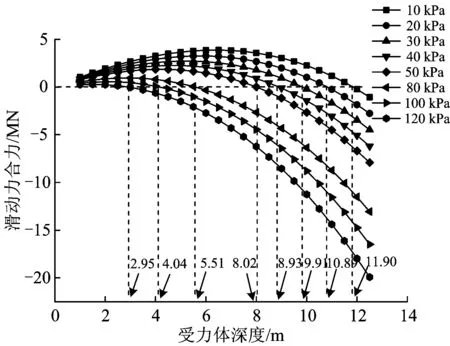
圖11 不同黏聚力、不同受力體深度的滑動(dòng)力合力

由圖11可見：隨著黏聚力逐漸增加，樁前楔形受力體深度一定時(shí)，其所受的滑動(dòng)力合力逐漸減小。

依據(jù)圖11，得到的不同黏聚力條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段樁長ypcr見表4，相應(yīng)曲線如圖12所示。

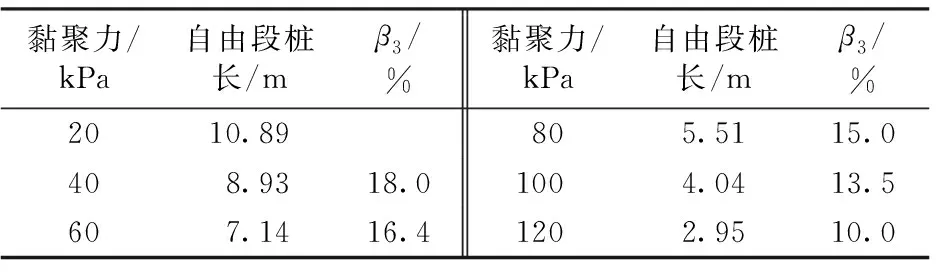
表4 不同黏聚力對應(yīng)的自由段樁長

注：β3為黏聚力每增長20 kPa自由段樁長的減小百分比。

圖12 不同黏聚力時(shí)橋梁樁基的自由段樁長

由表4可知：黏聚力每增加20 kPa時(shí)，對應(yīng)的自由段樁長分別減小18.0%，16.4%，15.0%，13.5%和10.0%。

由圖12可見：隨著黏聚力的增加樁基自由段樁長逐漸減小，且隨著黏聚力增大，自由段樁長逐漸減小的趨勢逐漸變?nèi)酢?/p>

圖13為其他條件不變，不同等效寬度條件下受力體滑動(dòng)力合力FR隨受力體深度y的變化曲線。由圖13可見：隨著等效寬度逐漸增加，樁前楔形受力體深度一定時(shí)，其所受的滑動(dòng)力合力逐漸增加。

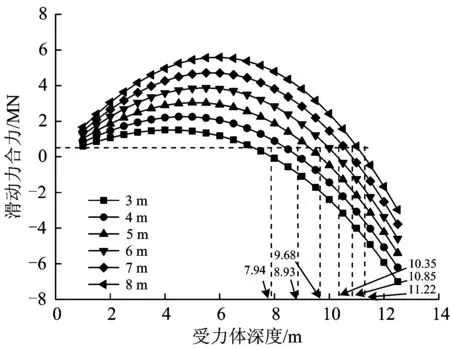
圖13 不同等效寬度、不同受力體深度的滑動(dòng)力合力

依據(jù)圖13，得到的不同等效寬度條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段樁長ypcr見表5，相應(yīng)曲線如圖14所示。

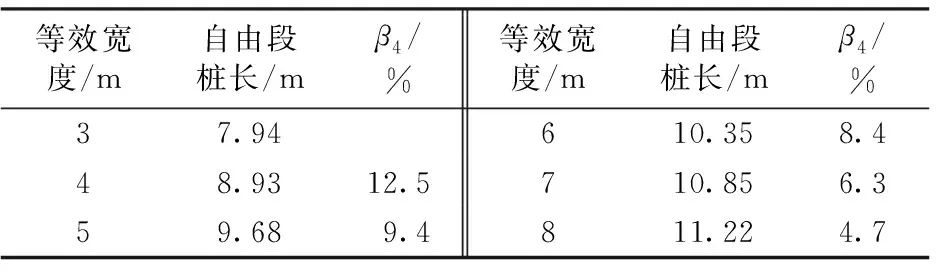
表5 不同等效寬度對應(yīng)的自由段樁長

注：β4為等效寬度每增長1 m自由段樁長的增長百分比。

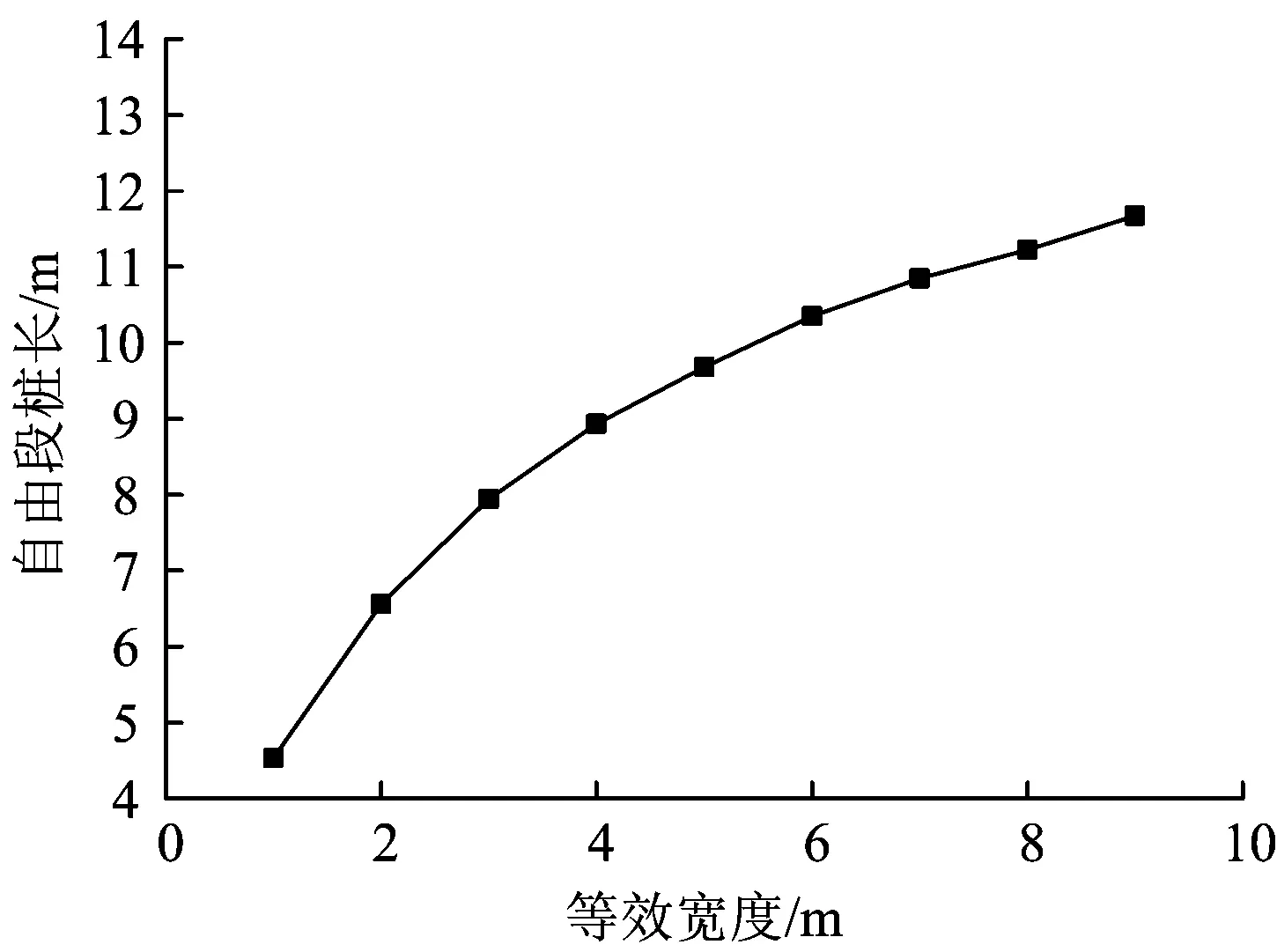
圖14 不同等效寬度時(shí)橋梁樁基的自由段樁長

由表5可知：等效寬度每增加1 m時(shí)，對應(yīng)的自由段樁長分別增加12.5%，9.4%，8.4%，6.3%和4.7%。

由圖14可見：隨著等效寬度的增加樁基自由段樁長增大，且隨著等效寬度增長，自由段樁長逐漸增加的趨勢逐漸放緩。

圖15為其他條件不變，不同接觸壓應(yīng)力條件下受力體滑動(dòng)力合力FR隨受力體深度y的變化曲線。由圖15可見：隨著接觸壓應(yīng)力逐漸增加，樁前楔形受力體深度一定時(shí)，其所受的滑動(dòng)力合力逐漸增加。

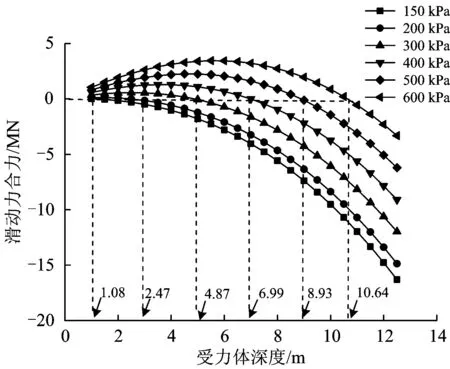
圖15 不同接觸壓應(yīng)力、不同受力體深度的滑動(dòng)力合力

依據(jù)圖15，得到的不同接觸壓應(yīng)力條件下受力體所受滑動(dòng)力合力為0時(shí)對應(yīng)的受力體深度，即斜坡橋梁樁基自由段樁長ypcr見表6，相應(yīng)曲線如圖16所示。

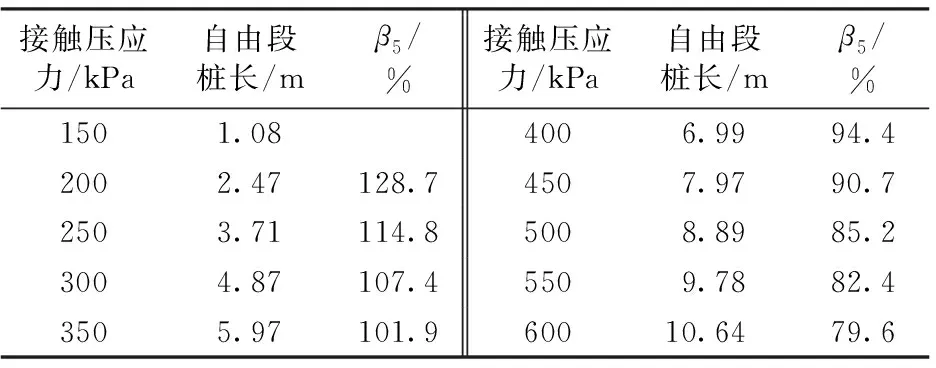
表6 不同接觸壓應(yīng)力對應(yīng)的自由段樁長

注：β5為接觸壓應(yīng)力每增長50 kPa自由段樁長的增長百分比。

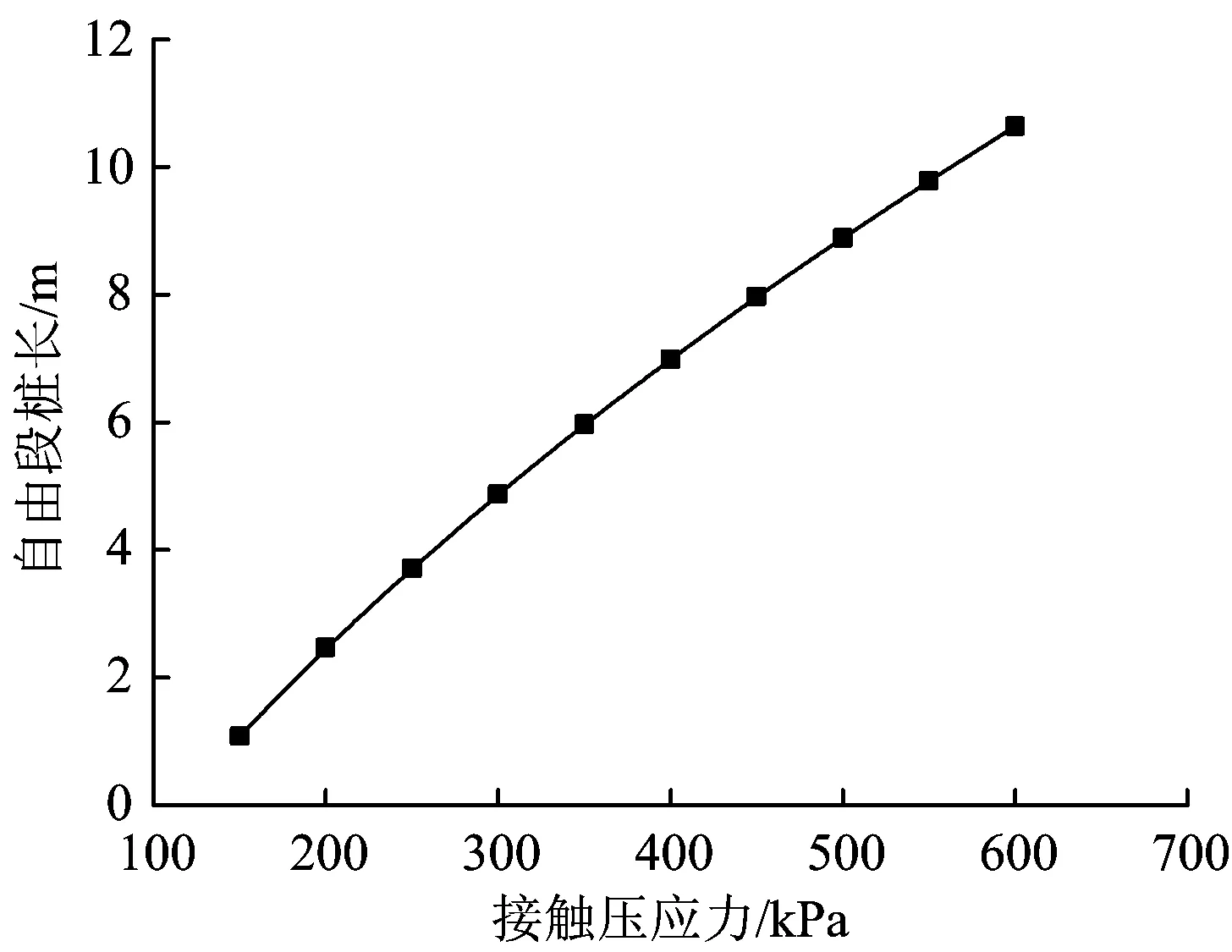
圖16 不同接觸壓應(yīng)力時(shí)橋梁樁基的自由段樁長

由表6可知：接觸壓應(yīng)力每增加50 kPa時(shí)，對應(yīng)的自由段樁長分別增加128.7%，114.8%，107.4%，101.9%，94.4%，90.7%，85.2%，82.4%和79.6%。

由圖16可見：隨著接觸壓應(yīng)力的增加樁基自由段樁長逐漸增大。

通過對上述6個(gè)因素的敏感性進(jìn)行分析，發(fā)現(xiàn)敏感性由高到低依次是斜坡坡角α、樁土接觸應(yīng)力σh、樁前土內(nèi)摩擦角φ、樁前土黏聚力c、樁截面等效寬度b和樁周巖土體重度γ。

3 工程實(shí)例

長昆鐵路客運(yùn)專線湖南段線路大多穿越山嶺丘陵地帶，地形、地質(zhì)條件復(fù)雜，一部分線路不可避免地毗鄰高陡的自然斜坡。其中，僅橋梁273座，部分橋隧過渡段、路橋過渡段都置于高陡斜坡之上，給斜坡橋梁墩臺(tái)設(shè)計(jì)帶來了極大的風(fēng)險(xiǎn)。

設(shè)計(jì)采用本文所建立的斜坡樁基礎(chǔ)自由樁長計(jì)算模型，運(yùn)用研發(fā)的自由樁長計(jì)算軟件對部分高陡斜坡樁基的合理自由樁長取值進(jìn)行分析，若樁基的等效寬度均取6 m，一般完整巖石地基破裂時(shí)壓力擴(kuò)散角按45°進(jìn)行取值，部分設(shè)計(jì)工點(diǎn)自由樁長計(jì)算結(jié)果見表7。

表7 長昆鐵路客運(yùn)專線部分陡坡橋基自由樁長計(jì)算結(jié)果

計(jì)算結(jié)果表明，若橋基位于坡度較緩、地層較為堅(jiān)硬的坡地上，樁基內(nèi)力計(jì)算時(shí)基本可忽略自由樁長的影響；若斜坡較陡或斜坡巖土體強(qiáng)度較低時(shí)，計(jì)算出的自由樁長取值相對較大，須考慮自由樁長對樁基內(nèi)力計(jì)算的影響。與傳統(tǒng)單純憑借經(jīng)驗(yàn)或簡化二維計(jì)算模型相比，該方法可以方便地計(jì)算出斜坡樁基的自由樁長，為開展陡坡橋基樁基礎(chǔ)三維精細(xì)化內(nèi)力計(jì)算奠定了技術(shù)基礎(chǔ)。

4 結(jié) 語

本文以斜坡橋梁樁基自由段樁長的確定方法為研究目標(biāo)，依據(jù)橋梁樁基自由段樁長對應(yīng)深度范圍的樁前巖土體的幾何形態(tài)，將樁前自由段樁長范圍內(nèi)存在變形趨勢的巖土體視為三維楔形受力體，考慮樁前受力體的自重及兩側(cè)拉力、受力體底部的極限抗滑力和摩阻力、樁土間接觸壓應(yīng)力，推導(dǎo)其滑動(dòng)力合力計(jì)算式，依據(jù)受力體的臨界穩(wěn)定狀態(tài)確定斜坡橋梁樁基自由段樁長，并采用C#開發(fā)了斜坡橋梁樁基自由段樁長的計(jì)算程序。運(yùn)用該程序?qū)π逼聵痘杂啥螛堕L取值的影響因素進(jìn)行敏感性分析，結(jié)果表明：斜坡坡角、樁土接觸壓應(yīng)力、內(nèi)摩擦角對自由段樁長取值的影響較敏感，而樁周巖土體重度對自由段樁長取值的敏感性較小。采用本文提出的方法對對長昆客運(yùn)專線部分陡坡橋基自由段樁長的設(shè)計(jì)取值計(jì)算結(jié)果表明：當(dāng)斜坡坡度較緩、地層較為堅(jiān)硬時(shí)，位于其上的橋基內(nèi)力計(jì)算可忽略自由段樁長的影響；當(dāng)斜坡坡度較陡或斜坡巖土體強(qiáng)度較低時(shí)，計(jì)算得到的自由段樁長取值相對較大，斜坡橋梁樁基礎(chǔ)設(shè)計(jì)須考慮自由段樁長對樁基內(nèi)力計(jì)算的影響。

[1] 高宗余, 方秦漢, 衛(wèi)軍. 中國鐵路橋梁技術(shù)發(fā)展與展望[J]. 鐵道工程學(xué)報(bào), 2007(1):55-59.

(GAO Zongyu, FANG Qinhan, WEI Jun. Development and Prospects for Technology of Railway Bridge in China[J]. Journal of Railway Engineering Society, 2007(1):55-59. in Chinese)

[2] 鐵道第三偵察設(shè)計(jì)院.TB 10002.5—2005 鐵路橋涵地基和基礎(chǔ)設(shè)計(jì)規(guī)范[S].北京:中國鐵道出版社,2005.

[3] 王春雷, 謝強(qiáng). 橋基荷載作用下三維高邊坡巖體力學(xué)行為及橋基位置確定的研究[J]. 中國鐵道科學(xué), 2011, 32(2):136-138.

(WANG Chunlei, XIE Qiang. Study on the Three-Dimensional Mechanical Behaviour of the Rock Mass on High Slope under Bridge Foundation Load and the Determination of Bridge Foundation Position[J]. China Railway Science, 2011, 32(2):136-138. in Chinese)

[4] 鐵道部第一勘測設(shè)計(jì)院. 鐵路工程地質(zhì)手冊[M]. 北京: 中國鐵道出版社, 1999.

[5] 徐健強(qiáng). 黃土陡坡橋梁樁基礎(chǔ)設(shè)計(jì)[J]. 鐵道標(biāo)準(zhǔn)設(shè)計(jì), 2011(9):40-47.

(XU Jianqiang. Design of Bridge Pile Foundation on Steep Loess Slopes[J]. Railway Standard Design, 2011(9):40-47. in Chinese)

[6] BROMS B B. Lateral Resistance of Piles in Cohesive Soils[J]. Journal of Soil Mechanics and Foundation Engineering, 1964,90(2):122-155.

[7] BROWN D A, MORR I C. Lateral Load Behavior of Pile Group in Sand[J]. Journal of Geotechnical Engineering, ASCE,1988,114(11):1261-1276.

[8] ASHOUR M, NORRIS P. Modeling Lateral Soil-Pile Response Based on Soil-Pile Interaction[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(5):420-428.

[9] 藺鵬臻,武發(fā)輝, 楊子江. 考慮邊坡效應(yīng)的橋梁樁基受力分析[J]. 中國鐵道科學(xué), 2016, 37(4):54-60.

(LIN Pengzhen, WU Fahui, YANG Zijiang. Mechanics Analysis of Bridge Pile Foundation Considering Slope Effect[J]. China Railway Science, 2016, 37(4):54-60. in Chinese)

[10] 重慶市建設(shè)委員會(huì)，重慶市國土資源和房屋管理局. DB 50/5029—2004 地質(zhì)災(zāi)害防治工程設(shè)計(jì)規(guī)范[S].重慶:重慶市國土資源和房屋管理局，2004.

[11] 周春梅, 殷坤龍, 簡文星. 滑動(dòng)面傾斜時(shí)抗滑樁彈塑性區(qū)臨界高度的計(jì)算[J]. 巖土力學(xué), 2008, 29(7):1945-1954.

(ZHOU Chunmei, YIN Kunlong,JIAN Wenxing. Calculation of Critical Height of Rock-Soil Elastoplastic Area before Anti-Slide Pile on Declining Sliding Surface[J]. Rock and Soil Mechanics, 2008, 29(7):1945-1954. in Chinese)

[12] 張永杰, 李侑軍, 趙明華, 等. 高陡斜坡作用下群樁基礎(chǔ)設(shè)計(jì)計(jì)算方法[J]. 中國公路學(xué)報(bào), 2014, 27(10):84-92.

(ZHANG Yongjie, LI Youjun, ZHAO Minghua, et al. Design and Calculation Method for Pile Group Foundation in High and Steep Slope[J]. China Journal of Highway and Transport, 2014, 27(10):84-92. in Chinese)

[13] 蔣爵光, 謝強(qiáng), 吳光. 北盤江大橋岸坡穩(wěn)定性及橋基選址的綜合分析[J]. 鐵道工程學(xué)報(bào), 1995(3):75-81.

(JIANG Jueguang, XIE Qiang, WU Guang. Synthesis Analysis on Stability of River’s Bank Slopes and Disposition of Bridge Foundations for Beipanjiang Railway Bridge[J]. Journal of Railway Engineering Society, 1995(3):75-81. in Chinese)

[14] 趙文, 謝強(qiáng), 龍德育. 高陡岸坡橋基合理位置確定方法[J]. 中國鐵道科學(xué), 2004, 25(6):94-98.

(ZHAO Wen, XIE Qiang, LONG Deyu. Method for Reasonably Positioning Bridge Foundation on High-Steep Slope[J]. China Railway Science, 2004, 25(6):94-98. in Chinese)