一種改進的碼率兼容QC-LDPC碼構造算法

范仁基，趙旦峰

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001)

0 引言

LDPC碼(Low-Density Parity-Check code)[1]是目前最為接近Shannon極限的一種糾錯碼，受到人們極大的重視。近年來，為了更好地適應各種通信系統多速率要求，LDPC碼的碼率兼容特性成為了一個研究和實現要點[2]，特別是隨著無人機被廣泛地應用于各領域[3]，研究具有碼率兼容的LDPC碼意義重大。

目前多碼率的實現方法主要有3種：刪余型、擴展型和縮短型。刪余型是目前應用最為廣泛的碼率兼容形式，通過選取一個性能優異的低碼率母碼，然后對校驗位進行刪余打孔處理實現多碼率，這樣可以節省存儲空間，但在刪余打孔時，存在產生大量陷阱集[4-5]導致性能惡化的問題；擴展型是通過擴展矩陣或校驗節點分裂方式實現，有效地克服了刪余型存在的問題，但也造成了需要存儲多個校驗矩陣[4]，大量占用硬件資源的問題；縮短型不同于前兩者，是通過對輸入的信息序列進行處理實現多碼率，其雖然克服了擴展型帶來的矩陣存儲問題，卻也因為需要信息序列預處理而增加了編譯碼的復雜度。因此有必要找到一種能夠較好地兼顧多碼率性能以及硬件資源占用的LDPC碼。本文將PEG算法與準循環法相結合[6]，通過正逆向兩次使用PEG算法構造具有下三角形式的準循環校驗矩陣，在實現多個碼率兼容的同時，各碼率下碼字性能與同參數下的準循環矩陣性能接近，而且其硬件實現較之前的QC-LDPC碼更為簡單，碼率控制更為靈活，尤其適合于硬件資源有限且通信環境復雜的無人機使用。

1 LDPC碼概述

LDPC碼是一種線性分組碼，若其對應校驗矩陣為H，則其生成矩陣G唯一確定，其碼長為n，信息序列長為k，校驗矩陣H的維數為m×n,m=n-k。二元域GF(2)上的一個3×6校驗矩陣可以如圖1所示，當存在序列c滿足HcT=0時，c為該LDPC碼的一個碼字。

圖1 3×6校驗矩陣

LDPC碼的另一種描述形式為Tanner圖[7]，一種由變量節點、校驗節點以及兩類節點間的邊構成的圖描述，如圖2所示。選取Tanner圖中某一節點為根節點，選取與之相連接的節點作為子節點并以邊相連，重復操作，直至沒有新生節點或出現重復節點為止，這樣就可以得到一個樹形展開圖[7]。樹圖可以更為便利地研究LDPC校驗矩陣的特性。

圖2 校驗矩陣的Tanner圖

在Tanner圖中，從某一節點出發，經過若干節點后返回此點為一循環(Cycle)，經過的邊的數目為這一循環的長度，而這其中最短的環長記為Girth，如圖2中所列舉的環，即為6環。由于LDPC的譯碼通常采用BP譯碼算法或基于BP算法改進而來的和積譯碼算法[7]，在譯碼時，某一節點的信息會經過最短的環路傳回自身，這樣就會破壞節點更新過程中信息的獨立傳播特性，導致譯碼收斂速度減慢甚至譯碼失敗。因此在構造LDPC碼校驗矩陣時，要盡可能地消除短環，增大最短環長Girth。

2 QC-LDPC碼校驗矩陣的結構和特性

QC-LDPC(Quasi-Cyclic LDPC)碼是一種基于循環置換矩陣的LDPC碼，由單位陣的循環置換矩陣和零矩陣構成其校驗矩陣[8]。以mb×nb維的準循環LDPC碼的校驗矩陣H為例，可以表示為式(1):

(1)

式中，I(Pij)(1≤i≤m,1≤j≤n)是一個右循環移位的b×b維方陣，可以通過單位陣I的每行經過Pij次右移得到，當Pij=0時，I(Pij)為單位陣，當Pij=-1時，I(Pij)為零矩陣。

由此也可以得到另外兩個重要矩陣，即由Pij組成的循環移位參數矩陣(2)以及基矩陣(3)：

(2)

(3)

而當這兩個矩陣被確定的同時，LDPC的校驗矩陣也隨之確定下來。通過對比LDPC校驗矩陣H與其基矩陣A，不難發現這二者具有相同的度分布[9,10]，而且其循環移位參數矩陣P具有如下特性：

若在一個循環塊邊長為b的QC-LDPC校驗矩陣的Tanner圖中，存在一條長度為2l的環，那么其循環移位參數矩陣P中同樣存在這樣環的充要條件[10]為:

(4)

根據這一特性，在基矩陣確定的條件下，校驗矩陣的最小環長不小于其基矩陣中的最小環長。因此可以通過調整循環移位參數矩陣P中各元素的數值，從而進一步消減短環擴大Girth，提升QC-LDPC校驗矩陣的性能。

3 PEG算法

PEG(Progress Edge Growth)算法[6,11-12]是在Tanner圖中選取一點為起點，在確保從該點出發的環長最大的條件下，不斷向節點之間添加邊的一種算法。PEG算法可以很好地保證任意一點的環長盡可能大，從而盡可能地增大Girth。

圖3 PEG算法的構造流程

PEG算法的復雜度會隨碼長增加而急劇增高，因此該算法通常用于中、短碼構造，而且構造過程中對于校驗矩陣的全局優化不足，容易產生大量公共節點，因其環分布復雜，也會對矩陣性能造成一定降低。特別是由于PEG采用隨機構造方法，導致校驗矩陣缺乏結構性，硬件實現復雜度高，更不利于在無人機LDPC碼中使用。

4 改進的碼率兼容QC-LDPC碼構造

PEG算法在中、短LDPC碼構造上表現優異，其本身最大缺陷在于硬件實現復雜度高，而QC-LDPC碼在工程實現性上有很大優勢，剛好可以對PEG法進行一定彌補，同時PEG算法也可以為QC-LDPC提供更大的圍長，因此可以將兩種構造方法相結合，進行聯合構造。本文首先采用PEG算法，構造一個高碼率校驗矩陣的基矩陣，然后在其基礎上，進行碼率擴展構造出碼率兼容的基矩陣。

但由于基本的PEG算法本身并不適用于碼率兼容矩陣構造，而在校驗矩陣構造時，PEG算法可以有效地控制最短環的長度，這給構造碼率兼容的LDPC碼校驗矩陣奠定了良好基礎，因此這里提出一種逆向PEG算法，可以在不改變最短環長的條件下，降低校驗矩陣的碼率以實現校碼率范圍的擴展。

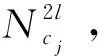
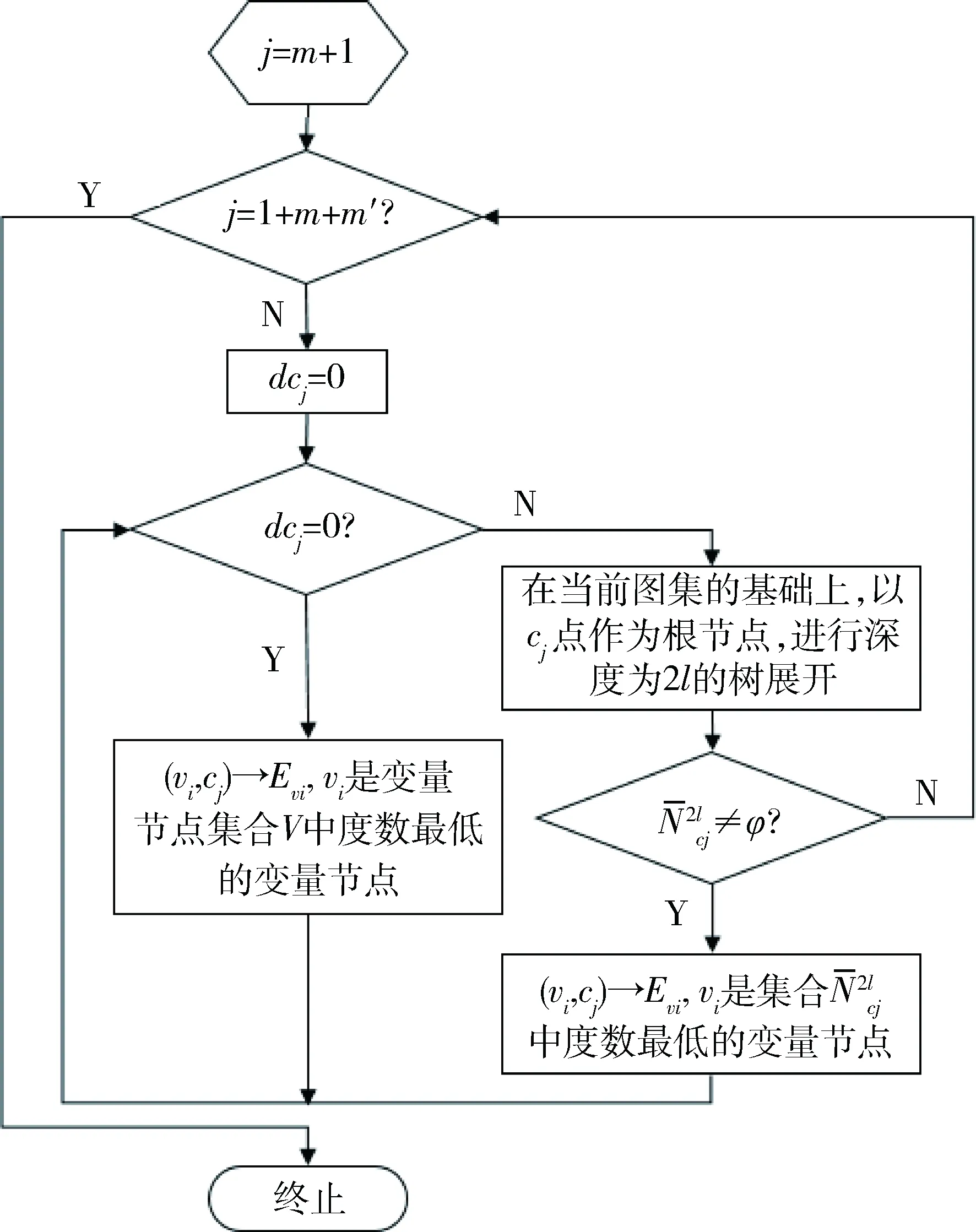
圖4 逆向PEG算法流程圖

通過分析算法流程可知，逆向PEG算法中對于每個新增的校驗節點除第一次添加邊是直接選擇度數最低的變量節點外，都是在進行深度為2l的樹展開后，才向新校驗節點添加新邊，這樣可以有效保證新增校驗節點與原校驗矩陣所組成的環長度均是大于2l的，也從而確保了拓展后的LDPC校驗矩陣中Girth保持不變，僅增大校驗矩陣的平均環長，來提升校驗矩陣的性能。這樣就可以通過逆向PEG算法，實現碼率兼容基矩陣的構造，最后通過將基矩陣中的各“1”元素和“0”元素分別用循環移位矩陣以及零矩陣進行替換，最終完成碼率兼容的QC-LDPC碼的構造。

在對基矩陣進行擴展時，從本文第2節循環矩陣特性得知，通過合理地調整各循環移位矩陣的移位參數，可以實現對矩陣結構優化以及碼字性能的提升。下面通過Tanner圖進一步討論如何設置循環移位矩陣參數。

結合公式(4)，令：

ΔPiPj(t)=Pi,t-Pj,t

(5)

這樣可以得到另外一個重要性質[9]：校驗矩陣中H的Girth不小于2(l+1)的重要條件為：

(6)

因此若要使得Girth不小于2(l+1)，需要每次添加循環移位參數時確保式(6)成立，這樣才能盡可能消減矩陣內的短環。綜上所述，碼率兼容QC-LDPC碼的構造算法具體步驟如圖5所示。

圖5 改進的碼率兼容QC-LDPC碼構造流程圖

逆向PEG擴展得到基矩陣是在用PEG構造的高碼率基矩陣的基礎上得到的，使得基矩陣具備了多碼率兼容特性的同時，還確保了基矩陣中的最小環長不發生變化。而循環移位參數矩陣與零矩陣參與的替換過程，使得矩陣中的環長進一步增大，進一步減少了短環數量，提高了碼字的糾錯性能，也令其硬件可實現性得到很大簡化，更加利于資源受限的無人機等設備使用。

5 仿真結果與分析

本設計以信息序列長為288 bit，碼率涵蓋3/4、2/3、1/2進行仿真分析。以3/4碼率為母矩陣進行擴展構造，并使用MATLAB對矩陣性能進行仿真，得出該LDPC 碼分別在幾個不同碼率下的誤碼率性能，仿真曲線如圖6所示。此外，在1/2碼率下將本設計與IEEE 802.16e標準的LDPC碼(q=24，即信息序列長為288 bit) 以及DVB-S2標準的LDPC縮短碼(信息序列長為300 bit)進行性能對比研究，仿真曲線如圖7所示。為了便于比較，輸入信號為二進制偽隨機序列，編碼器采用BPSK調制，信道為AWGN信道，最大迭代次數為25，均采用最小和MS譯碼算法。

圖6 信息位長288 bit碼字性能

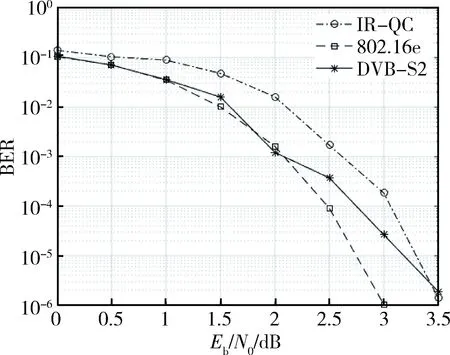
圖7 1/2碼率下LDPC碼性能對比

由圖6可見，本設計生成的碼率兼容QC-LDPC碼在其所涵蓋的3種碼率下都具有較為優秀的誤碼率性能，在BER=10-6時，3/4碼率與1/2碼率的LDPC碼的性能差異在1 dB左右。由圖7可知，相近碼長情況下，1/2碼率的碼率兼容QC-LDPC碼性能略差于DVB-S2標準的LDPC縮短碼，但是在歸一化信噪比為3.5 dB時二者性能一致。而與IEEE 802.16e標準的LDPC碼相比，在誤碼率為10-4～10-6的區間下，碼率兼容QC-LDPC碼的性能始終有著約0.5 dB的差距。綜上所述，本設計生成的QC-LDPC碼在保證性能優異的同時實現了多碼率兼容，具有良好的實用性。

6 結論

本文提出一種基于PEG算法的QC-LDPC碼構造方法，通過該方法可以構造出具有下三角結構的、兼容多個碼率及碼長的、且易于硬件實現的QC-LDPC碼。該構造方法通過正反向PEG算法來實現碼率兼容，并通過優化循環移位參數的設計，彌補PEG算法自身存在的問題，更進一步消除構造矩陣中存在的短環。仿真結果表明了該方法構造出來的QC-LDPC碼在幾種碼率下都具有較為突出的性能，且因為具有下三角結構，更加便于硬件實現，尤其適合于硬件資源受限條件下，這為無人機今后在多種傳輸條件下的廣泛應用提供了可能性。

[1] GALLAGER R G. Low-density parity-check codes[M].M.I.T. Press, 1963.

[2] 王琪，謝求亮，王昭誠.定碼長多碼率QC-LDPC碼的構造[J].清華大學學報(自然科學版)，2013(3)：394-398.

[3] 朱鐵林，秦凡，李鳳翔,等.應用于無人機測控傳輸系統的多元LDPC碼[J].電訊技術，2014(12)：1622-1626.

[4] LI J, NARAYANAN K R. Rate-compatible low density parity check codes for capacity-approaching ARQ scheme in packet data communications[C]//IASTED International Conference on Communications, 2002: 201-206.

[5] YAZDANI M R, BANIHASHEMI A H. On construction of rate-compatible low-density parity-check codes[J]. Communications Letters IEEE, 2004,8(3):159-161.

[6] 張建斌.基于PEG算法的準循環LDPC碼構造研究[J].電子器件，2012，35(6)：647-651.

[7] 賀鶴云.LDPC碼基礎與應用[M].北京：人民郵電出版社，2009.

[8] VASIC B, DJORDJEVIC I B. Quasicyclic low-density parity check codes[C]//International Conference on Telecommunications in Modern Satellite, 2005: 417-420.

[9] FOSSORIER M. Quasicyclic low density parity check codes[C].Proceedings in IEEE International Symposium on Information Theory, Yokohama, Japan, 2003: 150-151.

[10] 管武，項海格.具有大碼間距和大環路的QC-LDPC碼的構造[J].新能源進展，2011，16(4)：1-5.

[11] XIAO H, BANIHASHEMI A H. Improved progressive-edge-growth (PEG) construction of irregular LDPC codes[C]//Global Telecommunications Conference, 2004. GLOBEC, 2004: 489-492.

[12] HU X Y, ELEFTHERIOU E, ARNOLD D M. Regular and irregular progressive edge-growth tanner graphs[J]. IEEE Transactions on Information Theory, 2005, 51(1): 386-398.